货舱横梁模态仿真与实验对比研究

王新博 ，朱学斌 ，杨少东 ，王玉刚 ，安光乐 ，刘智云

(1．泰安航天特种车有限公司，山东泰安 271000；2.火箭军驻济南地区代表室，山东济南 250000)

0 引言

在车辆运输中，货舱是常用的装载工具，它一般通过支撑横梁将运载的货物质量传递到车架上。某货舱支撑横梁在使用过程中出现了焊缝开裂的情况，针对此情况，本文作者从有限元仿真和实验两个方面分析其原因，并提出解决方案。实验分为两部分：振动测试及静载逐级加载实验。

1 横梁振动特性的有限元仿真

该横梁承受的正常载荷为100 kN，由于下方需要通过变速箱到分动箱的传动轴而做了避让处理，出现了穹窿型的内凹形状，形成了承载上的薄弱环节，致使此处焊缝产生开裂。穹窿结构开口大的方向朝向车前，车架横梁三维图如图1所示。

首先建立横梁的有限元模型，通过仿真计算提取其前八阶模态[1]，位移云图如图2所示。

图1 车架横梁三维图

由图可知，第一阶模态的振动频率为317 Hz，振型表现为以车架中心线为对称轴的横梁整体上下弯折；第二阶模态的振动频率为562 Hz，振型表现为横梁整体做横向扭振；第三阶模态的振动频率为730 Hz，振型表现为以车架中心线为对称轴的横梁整体前后弯折；第四阶模态的振动频率为1 142 Hz，振型表现为前端单侧翼板的翘曲；第五阶模态的振动频率为1 216 Hz，振型表现为前端双侧翼板的翘曲；第六阶模态的振动频率为1 403 Hz，振型表现为双侧前后翼板的翘曲;第七阶模态的振动频率为1 498 Hz，振型表现为斜对角翼板的翘曲;第八阶模态的振动频率为1 578 Hz，振型表现为单侧前后翼板内侧上鼓。

图2 横梁前八阶模态图

2 振动实验测试

振动测试是在正弦波振动信号发生实验平台上进行的，并添加了相当于纵梁的夹具，以提高实验与实际情况的吻合性。由于实验台有自身的固有振动频率，会混杂到实验结果中，因此需要在实验结果中做甄别去除。

加速度传感器的布置如图3所示，在横梁试件左右两端分别为第1、2号测点，中间位置为第3号测点。测点1的振动加速度谱线如图4所示，振动加速度峰值及对应的频率列于表1。

图3 传感器布置图

图4 测点1振动加速度谱线图

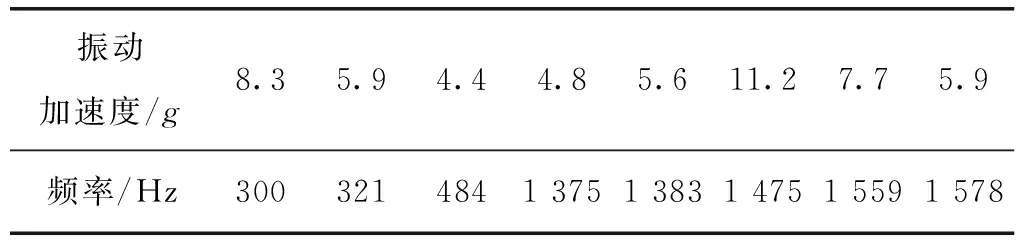
表1 测点1振动加速度峰值及对应频率

测点2的振动加速度谱线如图5所示，振动加速度峰值及对应的频率列于表2。

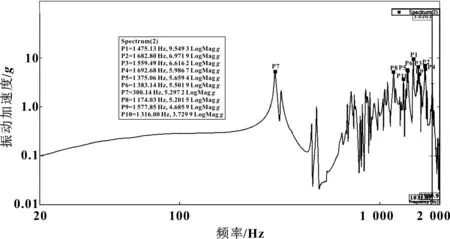
图5 测点2振动加速度谱线图

表2 测点2振动加速度峰值及对应频率

测点3的振动加速度谱线如图6所示，振动加速度峰值及对应的频率列于表3。

图6 测点3振动加速度谱线图

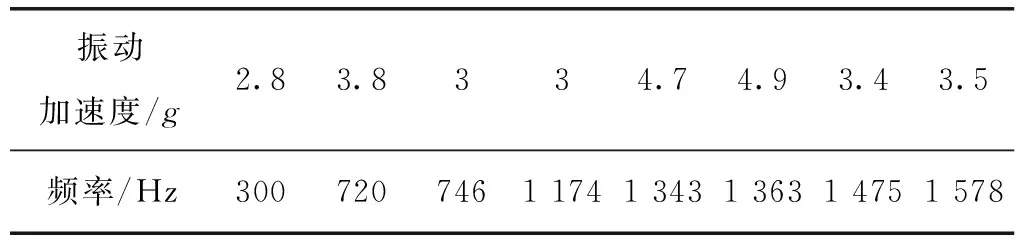
表3 测点3振动加速度峰值及对应频率

夹具1固有频率振动加速度谱线如图7所示，振动加速度峰值及对应的频率列于表4。

图7 夹具1振动加速度谱线图

表4 夹具1振动加速度峰值及对应频率

夹具2的振动加速度谱线如图8所示，振动加速度峰值及对应的频率列于表5。

图8 夹具2振动加速度谱线图

表5 夹具2振动加速度峰值及对应频率

由于测试结果中耦合了实验台的振动频率，需要通过对比分析滤除掉这些耦合的频率，然后参照仿真结果，得到横梁自身真实的固有振动频率，如表6所示。

表6 测点、试验台与仿真结果固有振动频率对照分析

对实验台耦合振动频率进行滤除后，以实验测得的频率值作为车辆行驶过程中该横梁固有振动频率的真值[2]，即表6最后一行所列出的频率值。

3 结论

分析有限元计算与实验测试方法所得部件固有振动频率存在部分偏差的原因：

(1)实验结果包含实验台固有频率的影响，需要甄别去除。

(2)试件与实验台及夹具采用四点螺栓固定，会使某些实验值略高，也使某些振型没有振起来。

(3)由于试件与实验台及夹具的耦合效应，会产生某些新频率。

(4)钢板厚薄不均，会使某些实验值略低。

(5)实际的材料密度与计算模型不完全一致。

(6)因为测点有限，实验中有些局部振动的高阶频率可能会漏测。

固有振动频率的仿真计算和实验结果基本一致，有限元仿真结果能清晰地看出包括几何体内部的所有节点的振动位移及整体振型[3]，而实验能把实际件的厚薄及密度反映到测值上，对二者取长补短加以结合，利用仿真结果将实验台的耦合频率滤除掉，得到部件真实的固有振动频率。从1 578 Hz这阶模态可以看出仿真计算与实验的结果都是准确的。

基频300 Hz的这阶模态表现为横梁左右对称的整体振动，远远高于车辆行驶时路面造成的振动频率。由于频率过高，一次冲击激起该频率的振动持续时间不长，不会形成共振。因此进行100、200、300 kN的逐级递增加载实验，从静力上解决该部件的破坏问题。