钢结构螺旋楼梯力学性能及极限稳定承载分析
2021-04-28林涛涛程俊婷
林涛涛,程俊婷,王 震
(1.浙江省建筑设计研究院,浙江 杭州310006;2.中机工程有限公司,浙江 杭州310016)
1 基本理论
板式钢结构螺旋楼梯由两侧梯梁和中间踏步板组成,两侧梯梁通过踏步板相连在一起,在空间上相互协调变形、共同受力。在力学模型上进行分解,梯梁在任何正截面上均受到轴力、弯矩、剪力、扭矩作用。其核心难点问题是杆件在扭矩作用下的截面应力分析。
1.1 扭转理论
扭转分为自由扭转(也称圣维南扭转)和约束扭转。自由扭转需同时满足以下两个条件:1)截面上受等值方向的一对扭矩作用;2)构件端部截面的纵向纤维不受约束[1]。不满足上述条件时即为约束扭转。实际工程中绝大部分的受力构件均为约束扭转,很少出现自由扭转。
对于钢质薄壁杆件(如箱型截面、工字型截面等),自由扭转的截面应力分析比较简单,即产生扭转剪应力,可得到解析解。约束扭转由于截面翘曲受到约束,会产生翘曲变形,从而在截面上产生翘曲正应力和翘曲剪应力,计算应力分析复杂。
1.2 分析方法
国内的钢结构设计规范针对钢结构薄壁杆件,未给出关于扭矩的抗力计算公式,仅在《钢结构设计规范(GB 50017—201X)》征求意见稿中给出相关公式,然而意见征求稿的抗扭计算公式复杂,并且仅针对特定情况下抗扭计算,并不具备较强实用性。《钢结构设计标准(GB 50017—2017)》在最终出版时,删掉了征求意见稿中关于抗扭的计算公式。
由于无规范公式,应力分析需要借助结构力学与材料力学计算,我们可以通过通用有限元程序进行分析。考虑钢结构螺旋楼梯的空间复杂性,可使用的结构分析软件有Ansys、Abaqus、SAP2000和Midas等。其中钢质梯梁的有限元模型可取梁单元模型或者壳单元模型;踏步板的有限元模型可取壳单元模型或者等效梁模型,也有将踏步板仅作为传递荷载而不计入结构整体分析中。
对于此种类型的空间钢结构螺旋楼梯,第一种模拟方法是采用杆系模型(即两侧箱型梯梁采用梁单元模拟,踏步板采用等效L型梁模拟),此模拟方法会将箱型梯梁截面上的翘曲正应力和翘曲剪应力忽略,而且踏步等效为L型梁与实际结构偏差太大。第二种模拟方法是采用壳单元模型两侧箱型梯梁,但是忽略踏步板的作用,此模拟方法忽略结构整体性,不考虑踏步板对两侧梯梁的协调作用。第三种模拟方法是全部采用壳单元模拟,能够按真实情况考虑,建模的工作量相对较大。综合考虑各分析软件的特点,本文选用通用有限元分析软件Ansys进行分析,采用参数化建模方式,梯梁及踏步板均选取壳单元进行分析。
2 正常使用时的受力性能分析
选取文献[2]中的钢结构螺旋楼梯算例(编号:BLTB-6015,层高6 m,总旋转角度540°),并进行改进,以更符合实际情况,满足建筑要求:将踏步板完全置于梯梁之上,并在踏步板上考虑50 mm的面层。取两侧箱型梯梁截面为446 mm×200 mm×16 mm,踏步钢板厚度为6 mm,钢材强度为Q345B。
2.1 参数选择
钢结构螺旋楼梯的箱型梯梁的两侧腹板及上下翼缘、踏步板拟采用壳单元来模拟。Ansys软件中壳单元类型很多,包括四节点单元(如shell181)、八节点单元(如shell93),有些可考虑剪切变形(如shell181、shell93),有些不含剪切变形(如shell63)。经综合考量,结合钢结构螺旋楼梯结构分析的特定需要,本文选用shell181单元来模拟。
Shell181单元是四节点3D壳单元,适合薄壳至中厚壳,并能考虑剪切变形。箱型梯梁腹板及翼缘属于中厚壳,踏步板属于薄壳,shell181均能适用。表面切向荷载加载时,可选用surf154单元,其效果仅传递荷载,不参与整体计算。
本例钢结构螺旋楼梯的平面内半径为1 m,外半径为2.5m,螺旋楼梯宽度1.5m,高度6m,螺旋间距4 m,顶部挑台长度2.5 m,整体旋转540°,采用螺旋上升形式,上、下两端固定约束。几何模型见图1。
2.2 有限元建模
2.2.1 荷载工况
1)自重及恒荷载。
钢结构构件的自重标准值由软件自动计算。
附加恒载标准值为50 mm厚的面层:25×0.05=1.25 kN/m2,防火涂料、钢质栏杆等,再附加均布恒载标准值0.5 kN/m2,合计1.75 kN/m2。
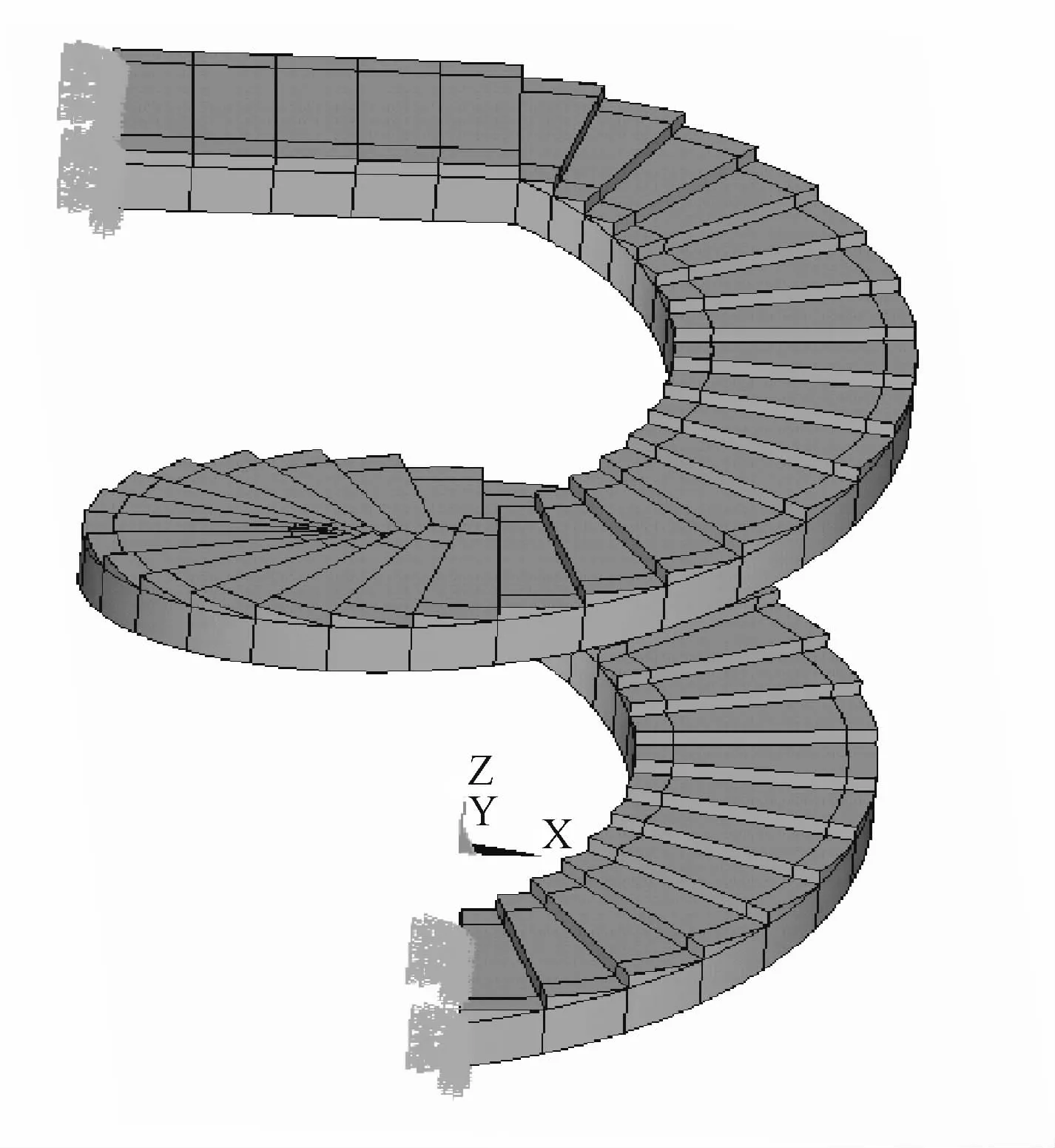
图1 几何模型
2)活荷载。
根据文献[3]表5.1.1,活荷载标准值取3.5 kN/m2。
3)荷载工况组合选取。
强度计算(应力大小):采用基本组合,即1.3×恒载标准值+1.5×活载标准值=1.3×1.75+1.5×3.5=7.525 kN/m2。
变形计算(挠度大小):采用标准组合,即恒载标准值+活载标准值=1.75+3.5=5.25 kN/m2。
2.2.2 模型建立
网格划分生成有限元模型,见图2。

图2 有限元模型
2.3 计算结果及分析
2.3.1 应力分析
强度计算的评价标准采用等效应力准则(Von Mises应力),应力云图见图3:最大应力达到223 MPa<295 MPa,对应最大应力比0.76<0.80,满足要求。
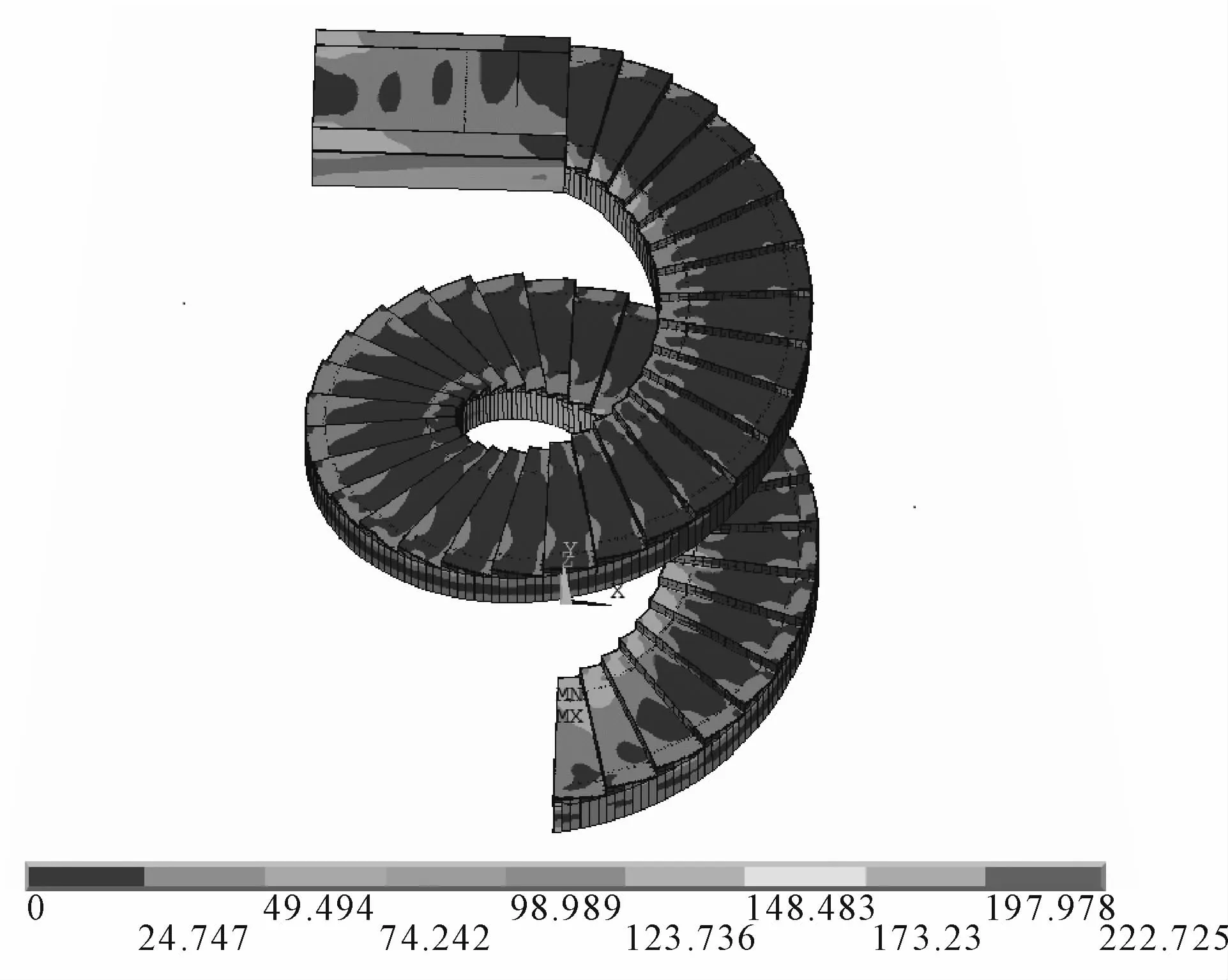
图3 Von M ises应力云图
2.3.2 变形分析
变形计算的评价标准采用竖向位移或者矢量位移,节点位移云图见图4:-Z向最大位移为18.6 mm,出现在螺旋楼梯中部位置的外侧梯梁,矢量最大位移为22 mm,最大位移与跨度之比1/306<1/250,满足要求。

图4 变形云图
2.3.3 薄弱部位
由计算可知,应力最大的位置靠近下部支座,变形最大的位置靠近螺旋楼梯中间高度位置的外侧,与概念分析一致。
3 非线性稳定极限承载分析
3.1 线性屈曲分析
线性屈曲分析(亦称特征值屈曲分析)计算简便概念清楚,有利于初步了解结构的整体稳定性。荷载采用D+L标准组合,前五阶特征值屈曲临界荷载系数(指屈曲临界荷载与所施加荷载之比)见表1。
图5为具有代表性的第1阶模态图。由图5可知,第1阶屈曲首先发生在下端支座附近的梯板上(即图中圆圈标注位置),此梯板为三边支撑板,且同时也是应力最大点附近,从概念上分析是合理正确的。总体上来说,屈曲模态是从下端支座逐渐往上部发展。

表1 前六阶特征值屈曲临界荷载系数(未全部列出)

图5 第1阶(荷载系数=15.708)
3.2 非线性屈曲分析
非线性屈曲分析,同时考虑材料非线性和几何非线性。材料非线性采用双线性随动强化模型。施加初始缺陷为第1阶特征值屈曲模态,采用弧长法进行计算。
图6为螺旋钢楼梯左侧中部位置梁单元节点的荷载系数a-u位移曲线变化图。由图6可知,螺旋楼梯整体结构荷载-位移呈线性变化,整体失稳变形不明显。本例Ansys在计算至荷载系数10.0时,Z向位移约为520 mm。
4 工程设计建议
1)在钢结构旋转楼梯设计中,应重视扭转作用的影响,需采用合适的计算软件进行分析及设计。工程设计中建议采用通用有限元软件,如Ansys、Abquas等软件进行计算分析,确保扭转效应能得到正确考虑。
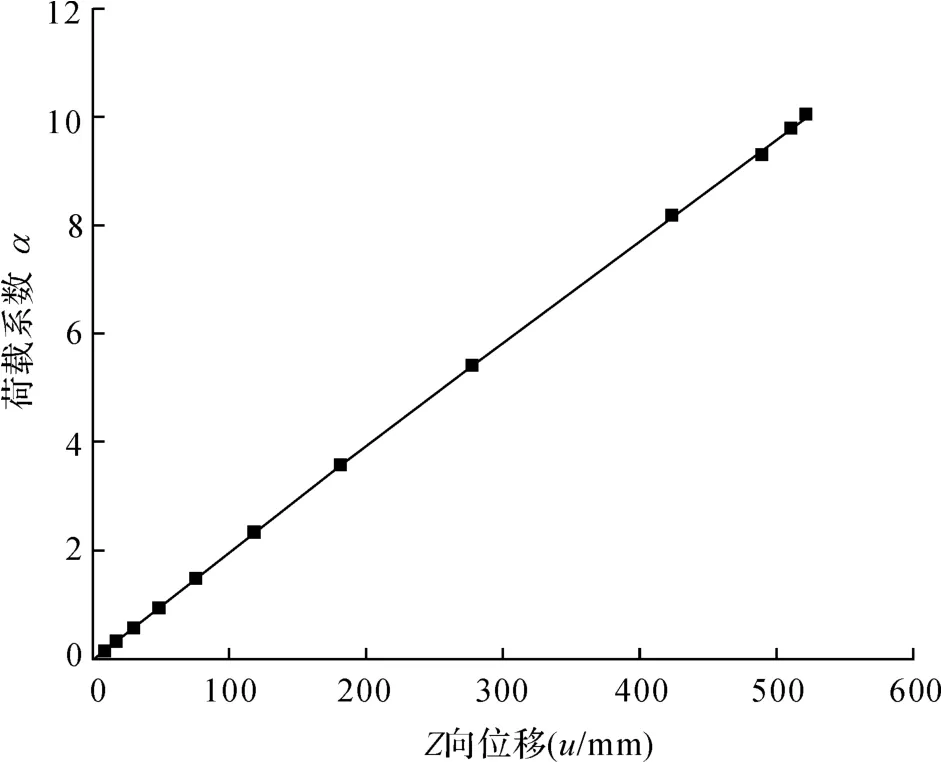
图6 荷载位移曲线
2)在螺旋楼梯的设计验算中,应重视结构变形的验算,应避免竖向变形过大影响正常使用。
5 结 语
1)钢结构螺旋楼梯的最大应力出现在底部固接位置以及上平台悬挑端部;钢结构螺旋楼梯的最大位移出现在中部位置。
2)钢结构螺旋楼梯端支座采用全固接设计,钢梯梁与支座埋板采用熔透焊方式。
3)在螺旋楼梯分析设计中,应考虑踏步板对于整体结构的刚度贡献,建模时将踏步板与两侧钢梯梁刚接,实际施工时采用等强焊接。
