固结灌浆工艺在岩溶地区船闸加固中的应用

降 英, 赵利平

(1.湖南省交通规划勘察设计院有限公司， 湖南 长沙 410200; 2.长沙理工大学， 湖南 长沙 410114)

0 引言

我国有许多在役水运工程建筑物修建于上世纪中叶，经过长期运营后，大多数建筑物已接近结构使用年限，亟需对其进行加固维修。岩溶作为一种特殊地质，在我国分布广泛，由于其特有的化学溶蚀和机械破坏作用，在附加荷载或振动作用下，将对建筑物地基稳定性产生破坏，给工程建设带来了严重威胁。近年来，固结灌浆加固措施在国内外已役水运工程结构加固修复中起到了重要作用。在工程加固修复现场监测中，常用应变计来监测结构应力。监测所得总应变除弹性应变外，还包括徐变应变、收缩应变等，而后者的应力应变关系与前者存在较大差别，因此必须将总应变进行应变分离。多年来，国内外很多学者做了深入研究，其中徐变系数一直是研究的热点。本文结合广东连江花溪船闸维修加固工程实例，对岩溶地基上在役船闸的固结灌浆加固稳定性进行研究，同时采用现场监测和数值模拟相结合的方法对加固效果作出科学分析总结。

1 工程概况

花溪船闸建成于1972年，位于广东省英德市阳山县西侧，是连江上梯级航运枢纽船闸之一。该船闸地处岩溶地基发育区，经多年运营后，闸室下溶洞顶板变薄，致使闸墙产生结构变形、墙身出现裂缝、闸室基底发生渗漏。本次维修采用固结灌浆对船闸进行修复加固:先对闸墙墙体进行外包混凝土加固以提高闸墙整体强度，为钻孔灌浆做准备；随后对闸墙岩溶地基进行固结灌浆，灌浆材料主要包含325#普通硅酸盐水泥、水、拌合剂和外加剂，将这些具有固化性质的浆液注入到岩溶地基的裂隙和空洞中，以达到船闸地基防渗、堵漏、加固、纠偏的目的，从而改善地基的物理力学性质。工程现场主要采用应变计对灌浆前后闸墙应变进行监测。

2 现场监测

2.1 测点布置

本次监测在花溪船闸闸室墙处进行，主要包括闸墙结构应变监测和裂缝应变监测。闸墙两侧埋设12只混凝土应变计，纵向间隔为2.2 m，应变计埋设于预先浇筑混凝土的钢筋网上；在船闸外闸墙内侧距闸墙顶部5.6 m处有一条较大裂缝，该处布置表贴式应变计，两端分别固定在裂缝两侧，测量裂缝的应变变化。测点布置如图1所示。

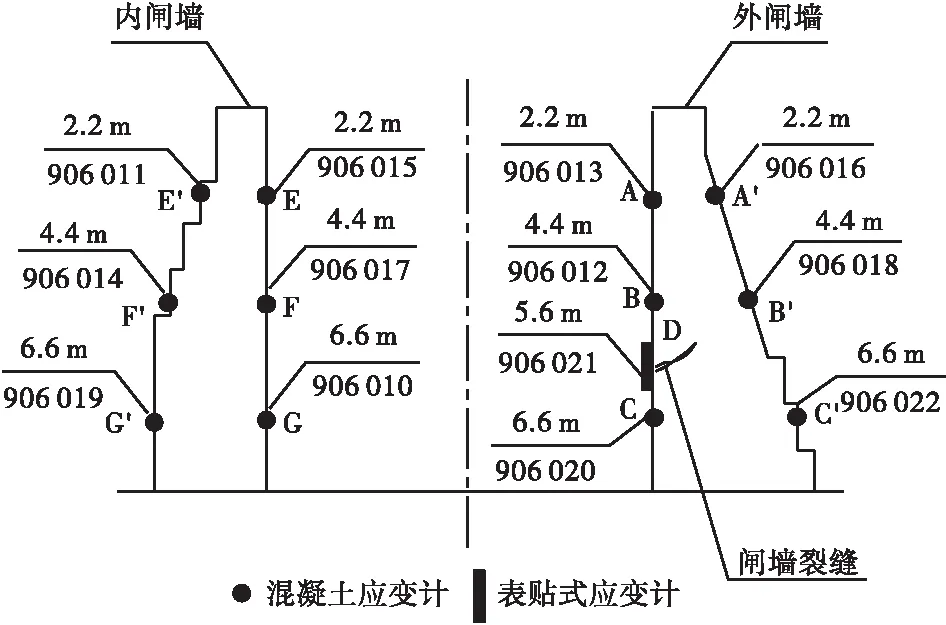
图1 闸墙断面应变计测点布置

2.2 应变分离

现场监测所得的总应变可以表示为式(1)所示：

εb(t)=εe(t)+εc(t)+εs(t)+εT(t)+εm

(1)

式中：εb(t)、εe(t)、εc(t)、εs(t)、εT(t)、εm分别表示混凝土的总应变、弹性应变，徐变应变、收缩应变、自由温度应变和测量系统误差应变[1]。

应变叠加原理指出混凝土收缩、温度应变与应力无关，而徐变应变则由应力作用引起，徐变与所施加的应力之间存在线性关系，且应力产生的应变满足叠加原理。有效弹性模量理论假定混凝土弹性模量和外荷载不随时间变化。徐变应变增量与应力增量之间关系表示如下[2]：

(2)

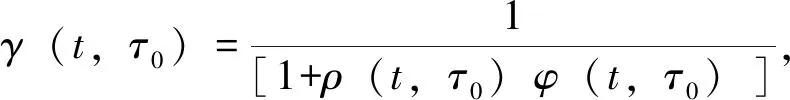
(3)

式中:φ(t，τ0)为收缩系数。考虑温度对混凝土结构的影响，温度应变的计算公式见式(4)。

ΔεT(t)=G(R1-R0)+(α1-α0)·(T1-T0)

(4)

式中:G为率定系数；R1-R0为度数变化量；α1为振弦材料的热膨胀系数；α0为混凝土结构的热膨胀系数，T1-T0为实测环境温度与初始温度之差[3]。

以测点B为例，根据式(1)～(4)对现场监测数据进行应变分离，得出混凝土弹性应变曲线(见图2)。由图2可知，混凝土弹性应变较总应变变化更为平缓，应变值基本在-22～-26 με范围内变化，但二者的变化趋势大致相同。以下分析采用的监测数据均为应变分离后的混凝土弹性应变。

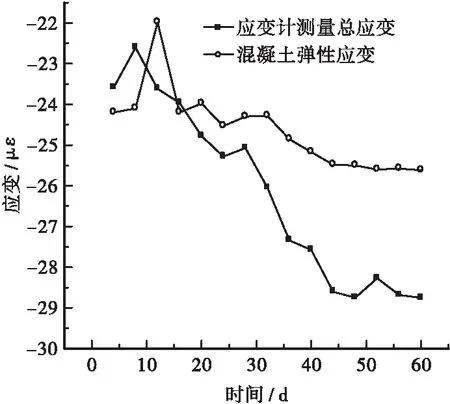
图2 监测数据应变分离曲线

3 有限元模型的建立

3.1 几何模型

根据船闸设计资料与地质勘测资料可知，闸室截面形状沿程变化不大，闸室地基中纵向分布有数个大小相似的溶洞。假设溶洞截面形状为圆形且纵向贯穿闸室，模型各力学参数分量均沿程不变。根据弹性力学的平面应变理论，模型可简化为二维平面问题[4]。数值模拟采用ANSYS有限元程序，闸室墙与地基网格划分均采用四节点平面单元(PLANE42)，以Drucker-Prager屈服准则对溶洞围岩进行非线性静力分析[5]。模型范围X为-31～31 m、Y为-20～8.6 m，且两侧边界条件为水平方向位移约束，底部边界条件为水平和竖直方向位移约束。内外闸墙均高8.6 m，基底宽分别为4.3 m和5.3 m，墙后填土高分别为5 m和2.5 m。岩基中溶洞半径均为2.5 m，溶洞顶板厚度分别为0.8 m和0.2 m。

3.2 材料参数的确定

参照《土工试验规程》(YS/T5 225—2016)[6]相关方法，现场试验测得地基、闸墙背填土、浆砌石、混凝土等材料参数(见表1)。在地基灌浆监测方面，采用声速仪测定岩石弹性波速传播速度，再根据弹性波速度计算出岩石的弹性模量，从而确定灌浆后基岩的物理力学性能[7-9]。灌浆14 d(5月30日)开始对地基进行测试，间隔时间为4 d，持续60 d。换算得到地基弹性模量(见表2)。由室内试验测得地基的其它力学参数在灌浆14 d后基本保持稳定，因此计算中取其平均值，泊松比取0.23，摩擦系数取0.65，重度取24.5 kN/m3。

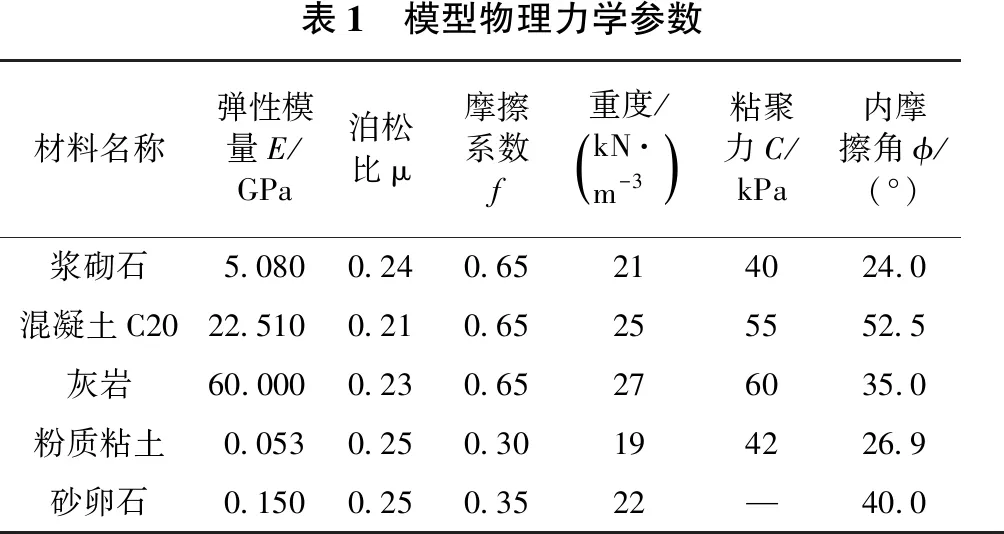
表1 模型物理力学参数材料名称弹性模量E/GPa 泊松比μ摩擦系数f重度/kN·m-3()粘聚力C/kPa内摩擦角ϕ/(°)浆砌石5.0800.240.65214024.0混凝土C2022.5100.210.65255552.5灰岩60.0000.230.65276035.0粉质粘土0.0530.250.30194226.9砂卵石0.1500.250.3522—40.0

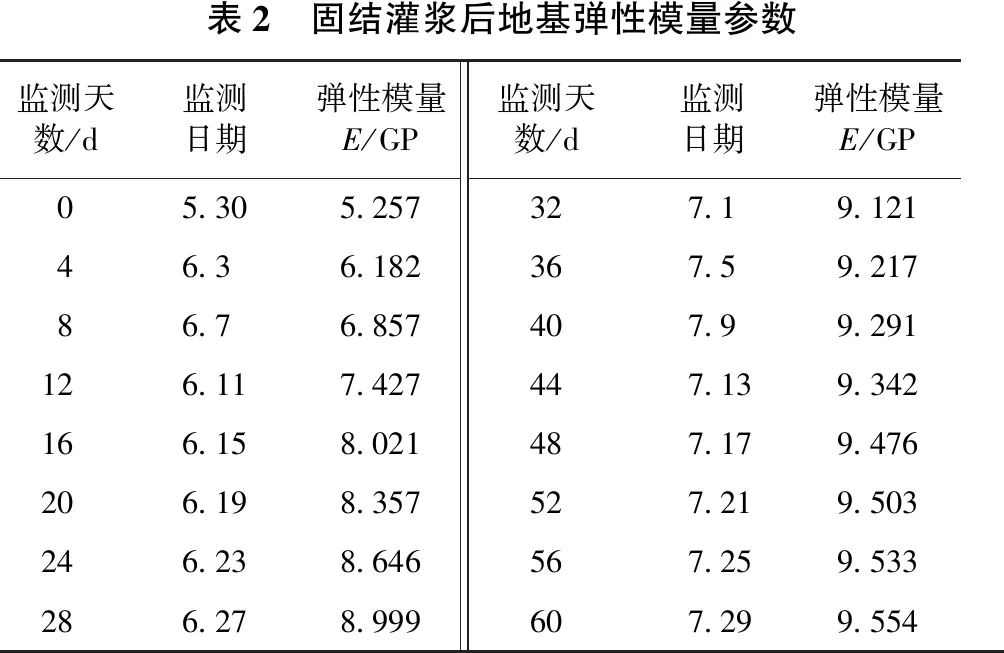
表2 固结灌浆后地基弹性模量参数监测天数/d监测日期弹性模量E/GP监测天数/d监测日期弹性模量E/GP05.305.257327.19.12146.36.182367.59.21786.76.857407.99.291126.117.427447.139.342166.158.021487.179.476206.198.357527.219.503246.238.646567.259.533286.278.999607.299.554

4 现场监测和数值模拟分析

4.1 数值模拟结果

闸墙各测点处对应应变值的有限元程序计算结果见表3。表中各应变均为测点处竖向弹性应变，与监测数据应变分离出的竖向弹性应变数据结果相对应。

1)从表3中看出，两闸墙内侧应变绝对值自上而下逐渐增大，并且外闸墙应变绝对值较内闸墙明显偏小，其原因主要是内侧闸墙墙后填土较高，作用于闸墙的土压力较大，因此在地基物理性质发生变化后，闸墙的应变变化幅度也较大。

2)地基灌浆前后，闸墙压应变有所增大，拉应变有所减小。两闸墙在E’点和G’点所受的最大拉压应变分别为23.352 με和-155.13 με。由《船闸水工建筑物设计规范》(JTJ 307—2001)[10]，闸墙背水侧可承受的最大拉应变和压应变分别为100 με和1 500 με，可知灌浆后闸墙拉压应变均处于安全状态。

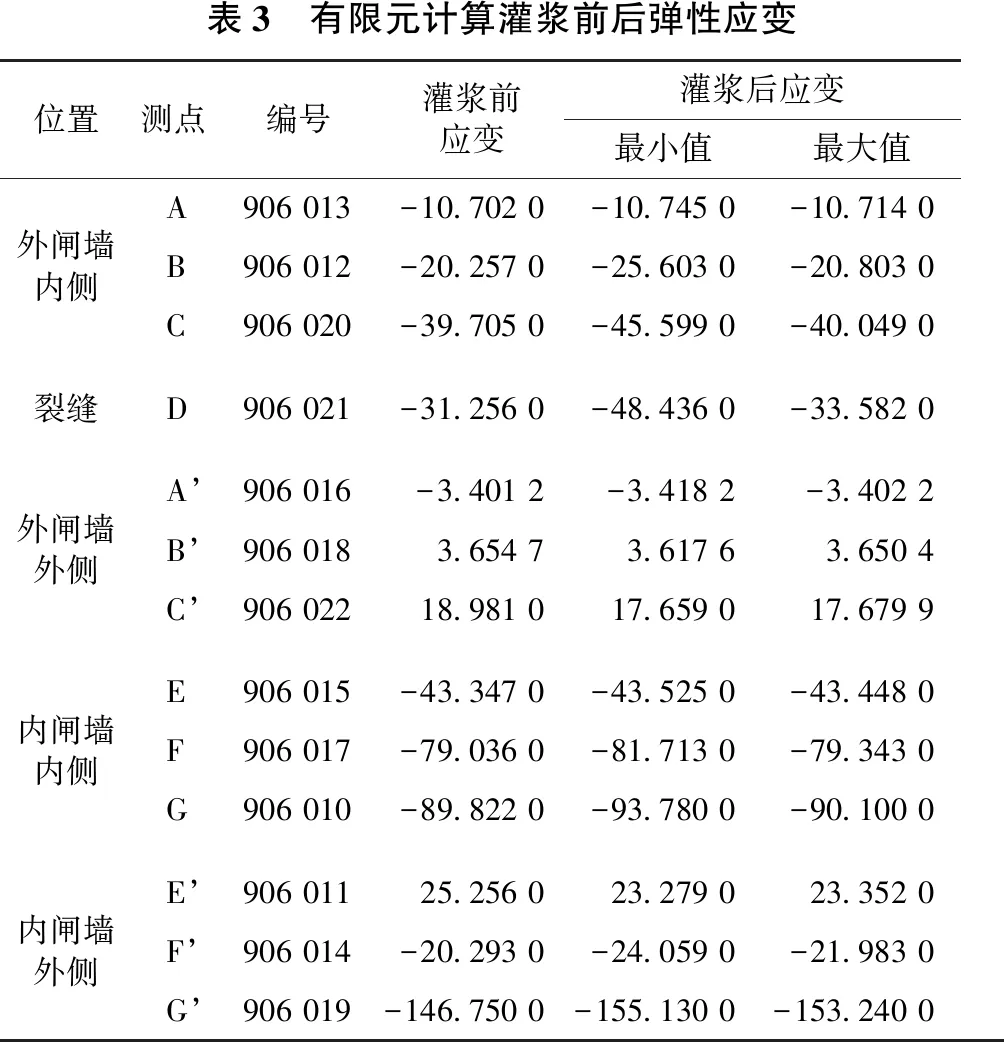
表3 有限元计算灌浆前后弹性应变位置测点编号灌浆前应变灌浆后应变最小值最大值A906 013-10.702 0-10.745 0-10.714 0外闸墙内侧B906 012-20.257 0-25.603 0-20.803 0C906 020-39.705 0-45.599 0-40.049 0裂缝D906 021-31.256 0-48.436 0-33.582 0A’906 016-3.401 2-3.418 2-3.402 2外闸墙外侧B’906 0183.654 73.617 63.650 4C’906 02218.981 017.659 017.679 9E906 015-43.347 0-43.525 0-43.448 0内闸墙内侧F906 017-79.036 0-81.713 0-79.343 0G906 010-89.822 0-93.780 0-90.100 0E’906 01125.256 023.279 023.352 0内闸墙外侧F’906 014-20.293 0-24.059 0-21.983 0G’906 019-146.750 0-155.130 0-153.240 0

4.2 结构应变分析

为研究地基灌浆加固后闸墙结构应变变化规律，分别取B点和F点作为内外闸墙典型分析点，B、F点累积应变曲线见图3～4。现场监测数据与数值模拟结果进行对比分析结果如下：

1)监测数据与数值模拟的累计应变曲线波动幅度和极值点不尽相同，但总体变化趋势基本一致。结构应变变化大致分为3个阶段：重分布阶段(约0～20 d)，应变值波动幅度较大；过渡阶段(约20～40 d)，应变值波动幅度明显减小；稳定阶段(约40～60 d)，应变值微小波动并逐渐趋于稳定。

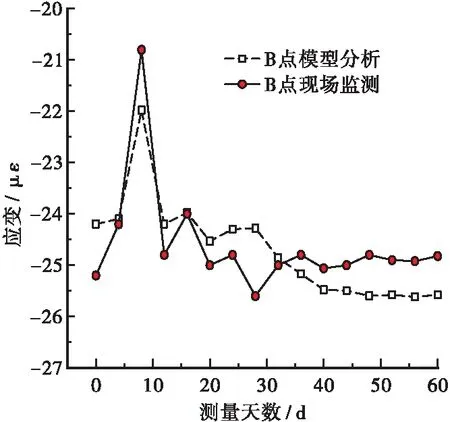
图3 B点累计应变曲线

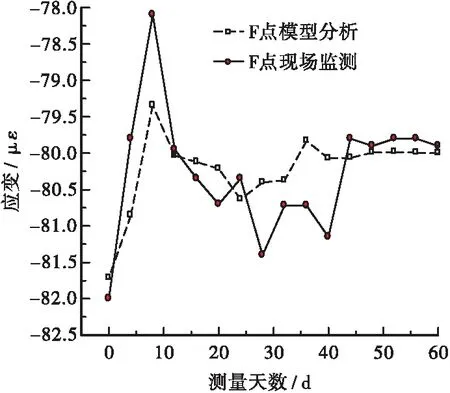
图4 F点累计应变曲线

2)B点监测数据与数值模拟结果符合较好。在重分布阶段，闸墙结构应变波动幅度较大，波动范围在-25.2～-20.6 με之间，其原因是地基弹性模量初期变化较大，引起闸墙结构应变的较大波动，后期逐渐达到稳定状态。

4.3 裂缝应变分析

闸墙裂缝处进行的现场监测数据与数值模拟结果对比如图5所示，分析结果如下：

1)由图5可知，监测数据与数值模拟结果的累计应变曲线总体趋势大致相同。裂缝压应变(应变绝对值)变化大致分为3个阶段：缓慢增长阶段(0～10 d)，应变基本保持在原来状态，略有小幅增长；快速增长阶段(10～30 d)，裂缝处压应变迅速增大，增幅最大为16 με；小幅波动阶段(30～60 d)，应变基本在-48～-46 με之间波动，并逐渐保持稳定。以上分析可知，随着岩溶地基力学性质显著改善，闸墙裂缝开裂程度得到有效地控制，该裂缝对闸墙结构安全没有构成影响。

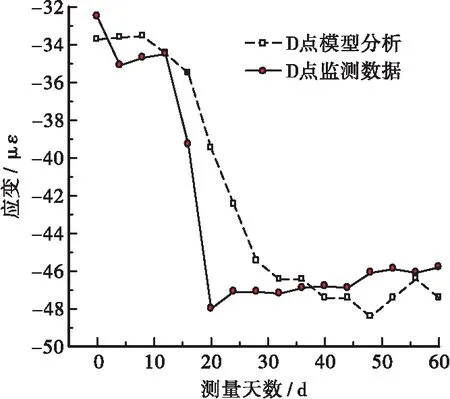
图5 D点累计应变变化曲线

在实际监测中，除应变分离所消除的混凝土徐变、收缩应变等影响外，现场机械施工、填土压力和水位变化等因素也会对应变计监测效果产生影响，其表现是应变曲线的异常波动，但总体趋势与数值模拟结果基本一致。

5 结论

地基固结灌浆对岩溶地区闸墙结构应变改善有积极作用。在役船闸固结灌浆加固措施有效控制了原闸墙岩溶发育趋势，闸墙的整体安全性有所提高，该措施切实有效。通过加固修复施工后，该船闸通航状态正常，运营状况良好，该工程的施工方法可为类似项目提供参考。