基于PCR与SVM的手写数字识别效果对比研究

李 想

（上海对外经贸大学，上海201620）

1 研究背景与目的

手写数字识别（Handwritten Numeral Recognition）是光学字符识别技术（Optical Character Recognition，OCR）的一个分支，也是常见的图像识别任务，其研究的目的是利用电子计算机自动辨认人工手写在纸张上的阿拉伯数字。通过计算机进行手写体数字识别可以节省大量人力和财力，因此国内外对手写识别单个算法的研究愈渐成熟[1-2]。

然而通过对大量相关资料进行查阅后发现，目前有关手写识别单个算法的研究文献较多，但多模型间进行比较的文献较难找到，因此不能够运用同一数据不同算法明显地反映出多个分类算法之间的准确度差异。主成分分析法（Principal Component Regression，PCR）主要利用降维的思想将多指标转化为少数指标（即主成分），其中每一个主成分均可反映出原始数据的部分信息，且这些信息互不重复[3]。支持向量机（Support Vector Machine，SVM）主要是以监督学习的方式使用分类与回归分析来处理数据的模型以及相关算法[4]。本文从机器学习的领域出发，旨在通过实验实现并比较PCR以及SVM两种手写数字识别算法模型的内容以及识别准确率，从而挑选出分类更加准确高效的方法。

2 实验设计与准备

2.1 设计思路

在PCR仿真实验中，通过主成分分析结合奇异值分解消去原变量间的共线性，对训练数据分类进行回归，使用不同的回归方程对样本进行预测，选择预测值最大的数为预测结果。在SVM仿真实验中，在数据样本之间选取最大间隔超平面进行分离，使用Sklearn模块训练并提取数据特征，建立模型，对样本进行不同参数的拟合，分析最终呈现的预测结果准确率。

2.2 基本方法

1）准备数据：数据来源于U.S.Postal Service数据库。原始图片由U.S.Postal Service的雇员扫描，有不同的分辨率和朝向，后被转为16×16像素的灰度图，并存储成纯文本的格式。

2）数据预处理：对准备好的数据进行归一化、标准化及降噪等处理，本文所用的数据集节选自Trevor Hastie,Robert Tibshirani和Jerome Friedman编写的书籍《The Elements of Statistical Learning》。

3）特征提取：原始数据通过映射或变换的方法将数字图像的特征从高维映射到低维，从而得到在特征空间中最能反映分类本质的特征。

4）奇异值分解：奇异值分解是将矩阵归约成其组成成分的矩阵分解方法，可适用于任意矩阵，使计算更简单。

2.3 符号说明

为进一步进行仿真实验，第66页表1和表2对模型中的符号进行解释说明。

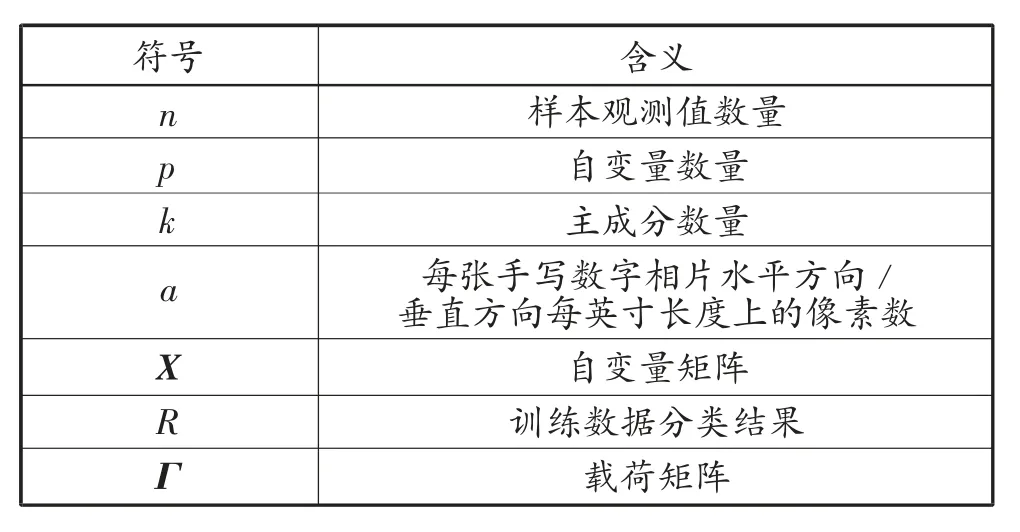
表1 模型一的符号解释说明

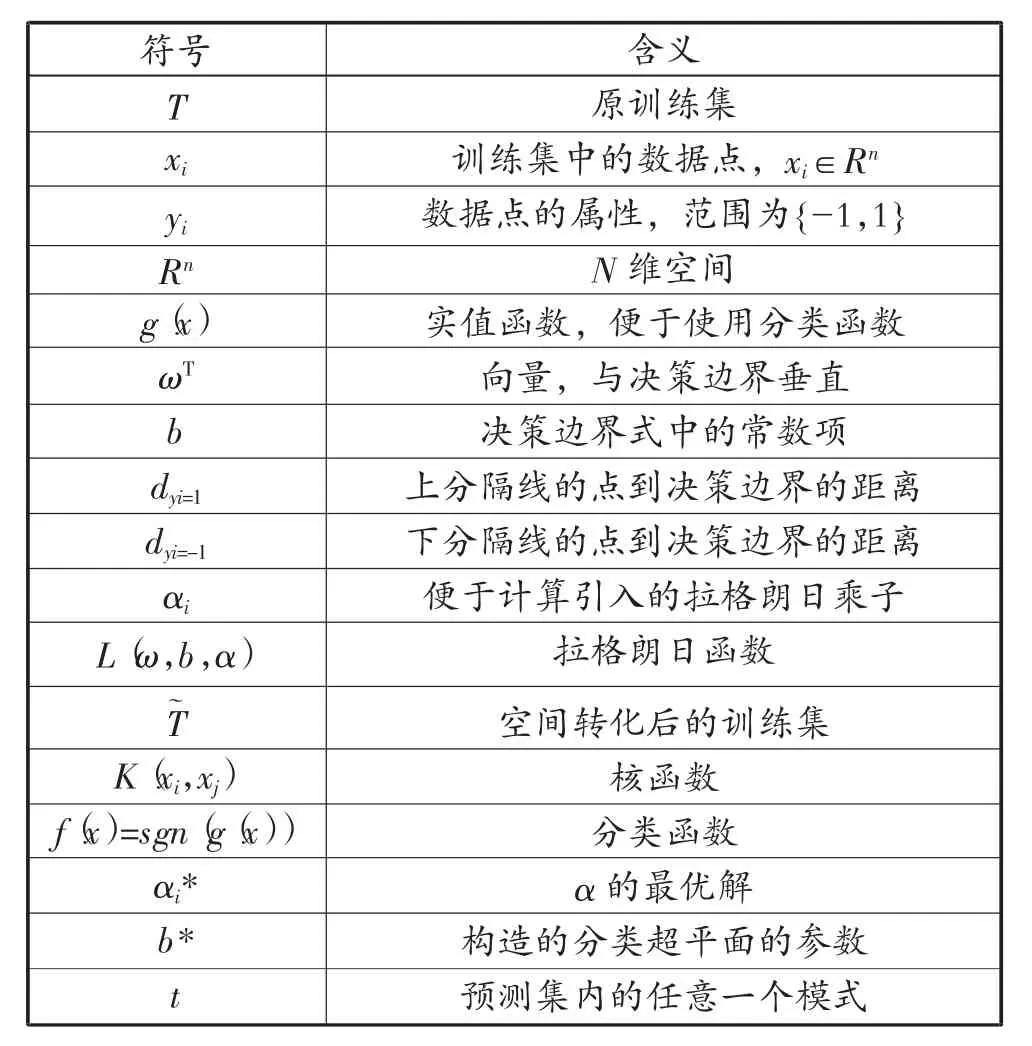
表2 模型二的符号解释说明

3 仿真实验过程

3.1 PCR的仿真实验过程

思路：基于训练数据进行分类得到不同结果的10种样本，通过对每组的多个自变量进行降维、将预测变量个数化为少数几个主成分后，得到10组因变量和自变量的回归方程，用它预测测试数据的因变量。每个测试数据可以得到10个结果，选取最大的预测因变量，则可以预测该图的真实值。

1）模型假设。假设样本观测值数量n大于等于自变量数量p，各自变量之间存在高度相关性。

2）模型建立。假设有n张手写数字相片，且每张相片的分辨率为a×a，设p=a×a。每个分辨率可视作一个自变量，每张相片可视作一个样本，则现有的n张手写数字相片的信息可储存在下列n×p矩阵中，其中，xij表示第i个样本的第j个自变量[5]。

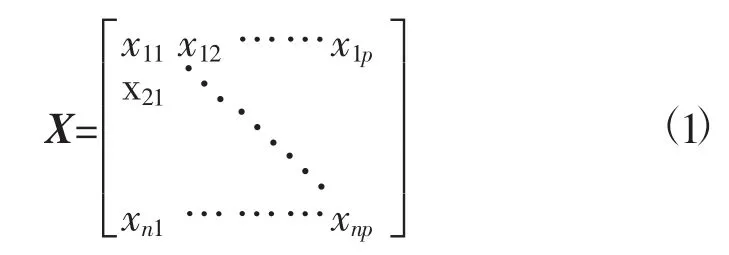
由于在矩阵X中n≥p，故对矩阵X进行奇异值分解（Singular Value Decomposition，SVD），分解后的矩阵为

式中：U和V分别为大小为n×n与p×p的正交矩阵，矩阵D满足

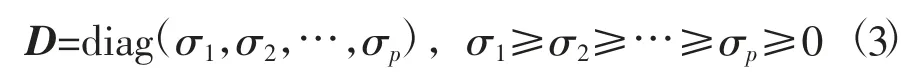
设矩阵U的前k列为Uk，矩阵V的前k列为Vk，矩阵D的前k个对角元素的对角阵为Dk，则有

由式（4）两边同时乘矩阵Γ可得

设矩阵Γ=Vk，可知

以XkΓ为自变量，对k个主成分进行线性回归，即可得到主成分的回归方程式，对其求解后即可得

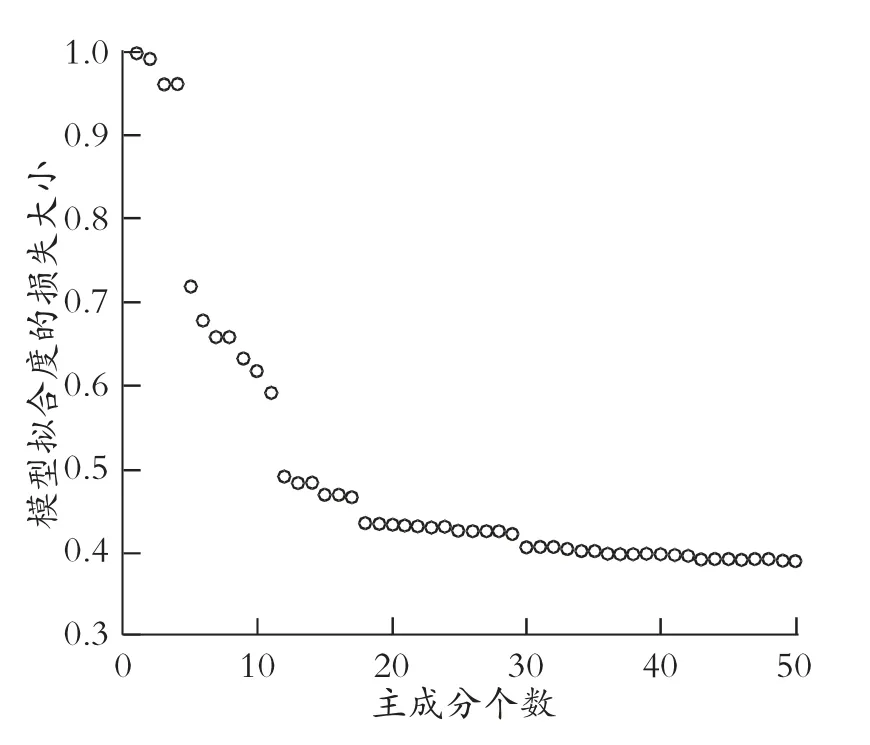
图1 模型拟合度损失大小

3）模型求解与仿真结果分析。根据训练数据可得n=1 707，p=16×16，根据主成分得分的计算、推导，通过R语言对k的取值进行遍历，进一步得到不同k值下模型拟合度的损失大小，见图1。

由图1可得，模型拟合度会随着主成分个数的增加而增加，但是增加的速度会随之减小。在本次问题中，选取主成分个数k为15，20，30分别进行求解。

把训练数据分成R={0，1，2，3，4，5，6，7，8，9}，对每种Ri进行主成分回归，得到10个回归方程。对每个样本，分别带入10个回归方程，得到一组预测结果为P={P0，P1，P2，P3，P4，P5，P6，P7，P8，P9}。

通过比较每个样本的P值得出样本的最大P值，若最大P值为Pi，则预测该样本为i。

根据运行结果可得，当主成分个数为15时，预测准确度为77.78%；当主成分个数为20时，预测准确度为81.07%；当主成分个数为30时，预测准确度为83.10%；之后随着主成分个数的增加，预测准确率也不会大幅度提升。分析可得，主成分分析很难精确地描述、分类、预测复杂的非线性的手写体数字特征。

3.2 SVM的仿真实验过程

思路：当存在一组数据集时，分类的途径是找到一条直线将样本的不同类别分开，由图2可以看出，b和c决策边界虽分开样本类别，但由于与某种类别的样本距离过近而分类效果较差。为保证良好的分类效果，决策边界需要与样本点距离保持最远，如a边界。

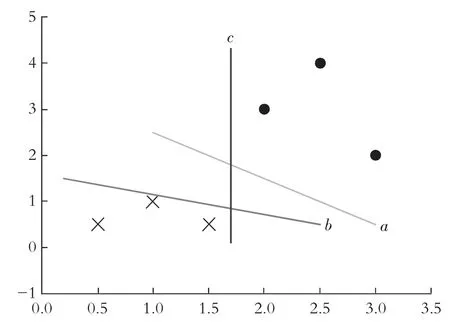
图2 不同决策边界分割效果对比图

1）模型假设。假设数据集可分。

2）模型建立。给定一个训练集T={[x1，y1]，[x2，y2]，…，[xm，ym]}。

输入空间中的每一个点xi由n个属性特征组成。yi∈{-1，1}，i=1，2，…，m表示数据的类别属性，对数据进行分类即寻找Rn上的一个函数g（x），使用分类函数推断任意一个模式相对应的y值。

∃ω∈Rn，b∈R使得空间内的决策边界可用·+b=0表示，+b=0为决策边界上所有的点[6]。

需要存在两条与最佳决策边界平行的线平均存在于最佳决策边界的两边保证最宽间距，距离最佳决策边界最近的点落在这两条平行线上，见图3。

图3 模型决策边界图示

由于只是平行上下的移动，且两条线与最佳决策边界等距，相当于在决策边界的表达式中加减同样的截距，假定截距为1，新的判定条件为

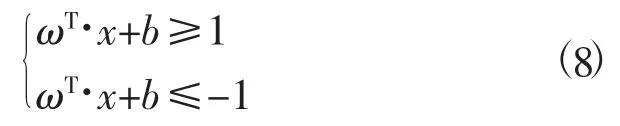
训练集中的点存在真实属性y，y的条件为

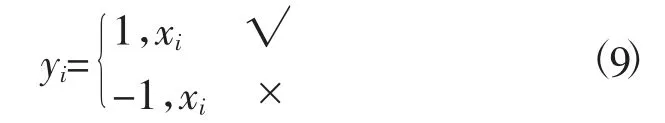
简化上式判定条件可得

在此判定条件的基础上，在上下两条平行线上分别取训练集中的一点xi，计算分类间隔。

点到线的距离公式为

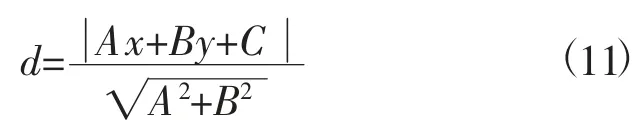
通过拉格朗日函数进行对偶问题的求解，引入新的系数作为拉格朗日乘子，把问题转化为对单一因子对偶变量的求解。引入新的系数为

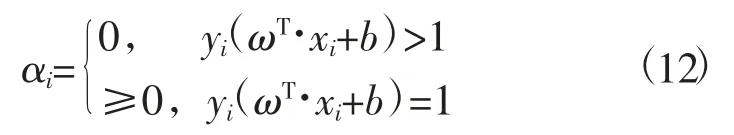
求最小值的问题可以转化成求参数α，使之满足以下函数方程组

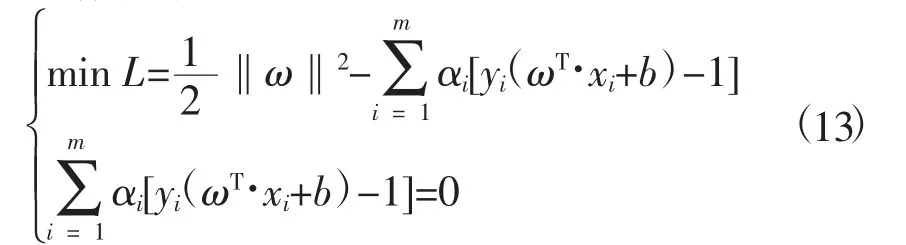
由以上对参数α的定义可知，只有当yi（ωT·xi+b）=1时，α才可以取到非零的值，且ω才可以非零，由此得知ω的取值只依赖于边界两条平行线上的向量，所以边界上的向量被称为支持向量。

训练集可能会出现非线性的情况，需要将训练集的输入空间变换成高位的希尔伯特空间，并引用核函数。转化后的高维空间中的训练集为

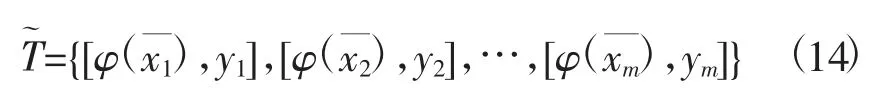
为了避免在高维空间中进行复杂的运算，采用的核函数K需要满足

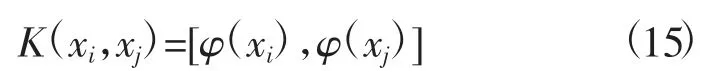
根据采用的手写识别数据训练集的特征数，引入高斯函数作为问题的核函数。

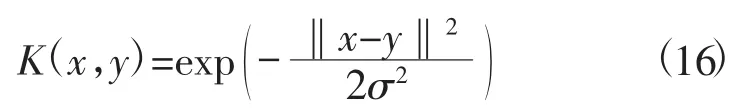
求解α的最优解并且构造分类超平面即可得到分类函数[7]为

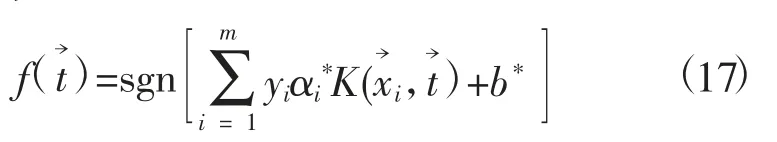
利用SVM算法分析训练集对分类函数进行求解后即可代入测试集进行结果的预测与分析。

3）模型求解与仿真结果分析。由于SVM的算法过于复杂，且现有程序中的SVM方法较为成熟，使用Python中的Sklearn包进行求解。将训练数据集中的每一个数字灰度值转换成256×1的一维数组，代入SVM模型，改变模型中的参数值：惩罚参数C设为100，30和1，核函数RBF的系数γ设为0.01，0.001，分别对模型进行训练，并使用测试集衡量不同参数训练后的SVM分类模型准确率，并生成准确率的混淆矩阵。

根据运行结果可得：

C=100，γ=0.01与C=30，γ=0.01的准确度相同，均为93.37%；

C=30，γ=0.001的准确度为92.07%；

C=1，γ=0.01的准确度为90.08%。

4 实验结果与分析

基于PCR实现手写数字识别主要使用R语言进行编程，基于SVM实现手写数字识别，考虑到算法复杂度，主要通过Python实现。基于PCR和SVM得出对每个数字的预测结果见表3。由表3和图4可得，对数字1的预测与分类，PCR优于SVM；对数字3，6和7的预测，两种方法预测准确率大体一致；对其他数字的预测，SVM优于PCR。综合以上实验结果，在该问题的数据集中，SVM的识别率要优于PCR。

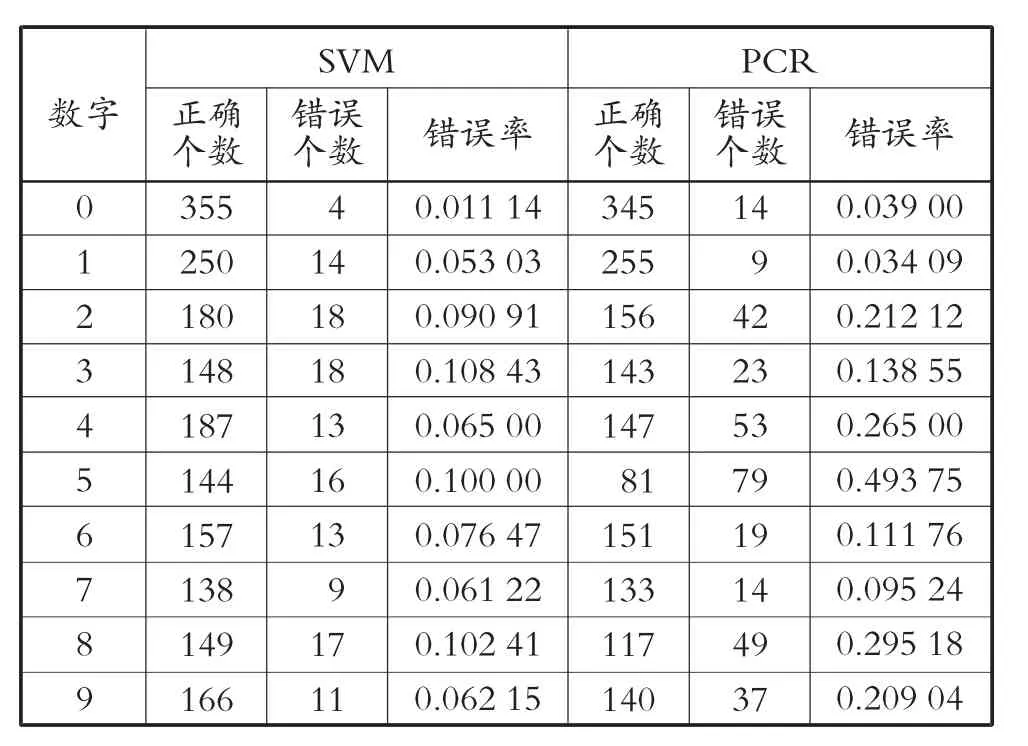
表3 两种方法对每个数字的预测结果

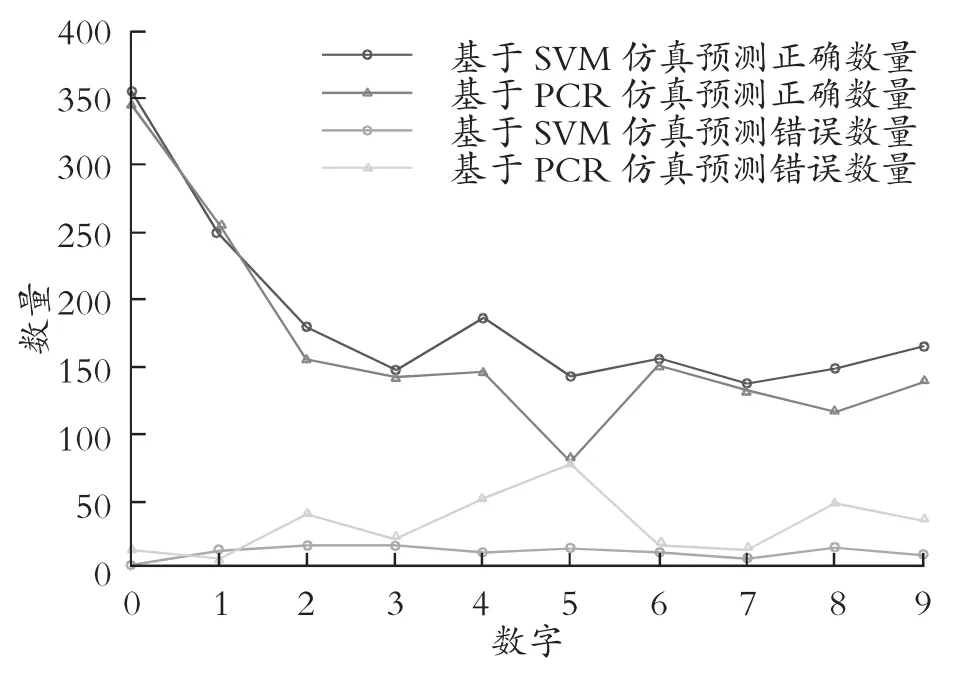
图4 基于PCR与SVM的预测效果比较图

总体而言，可以得出在实现手写数字识别中，虽然两者仍会出现较少的分类错误，但最终效果上基于SVM的方法预测和分类效果优于PCR。

5 结束语

从以上结果可以得出：PCR很难精确地描述、分类以及预测复杂的非线性的手写体数字特征，而SVM在本次问题的解决中表现得较优越。基于此，可以联想到主成分分析非线性扩展方法——核主成分分析。虽然这二者的主要目的都是降维而不是分类，但是在实验中也可用于分类。核主成分分析即是在主成分分析的基础上利用一个非线性映射将原始特征空间中的数据映射到高维特征空间中，然后在高维特征空间中进行主成分分析[8]。

在此次的两类仿真实验中，SVM的核函数采用高斯核函数，手写数字识别正确率为90%左右，高于PCR手写数字识别的正确率。对于需要高精度的领域来说，可以使用其他核函数进行进一步的改善和提升，而如何选择核函数需要进一步研究。