生活体验诠释数学本质

郭军明

[摘  要] 生活中蕴涵着丰富的数学知识、原理. 数学教学应适时地将学生的视野从课堂引向生活世界，寻找数学概念、法则、定律、公式、方法、思维的现实模型. 文章基于“现实背景与形式模型互相统一”的数学教学原则，在高中数学课堂教学中充分利用学生已有的生活体验，来解释数学原理、认识数学本质、体会数学价值.

[关键词] 数学本质;生活体验;高中;教学

数学体系的构建是由生活、生产的需要而产生的，以及它自身的逻辑演化而发展的，所以生活世界是数学体系的基础，是数学知识的意义之源，数学与现实生活有着难以割舍的联系. 从某种角度看，数学和生活的关系像是一个“映射”，也就是说数学总能找到在生活世界中的投影.

数学课程中设置有一定文字量的生活背景和应用实例，但很多教师把它们视为简单的“输入”和“输出”的教学环节，生活与数学两者的联系找不到相应的结合点. 在教学时应适时地将学生的视野从课堂引向生活世界，努力寻找数学概念、法则、定律、公式、方法、思维在客观世界中的模型，使学生理解数学知识、领悟数学思想、体会数学意义.

■认识数学语言的文化背景

1. 数学概念的文化背景

（1）体验数学概念的产生过程.

一切科学知识都是来自生活、受生活的启迪. 然而数学概念往往被抽象化的外衣包裹，但这些被包裹的概念常是有着其生动、具体的实际背景的. 在数学教材中许多概念（如集合、函数、导数、向量、数列、概率等）都是从丰富的、深厚的现实生活体验中引出的，所以数学概念教学要从学生的生活经验和已有知识出发，以学生已有的体验和容易理解的现实问题为素材，经历产生概念的过程，让学生在熟悉的事物和具体情境中理解数学概念的内涵.

（2）尝试数学概念的本意解释.

一般数学概念的定义都是严密的、精炼的，揭示本质属性的. 总是带着一副冷静的、刻板的面孔，然而我们的学生是一个个活生生的个体，有时两者往往产生一种无形的心理对立. 要使两者达成统一，只有让数学概念鲜活化和生动化.

①偶尔的一个英文注释，常常可以吸引对概念更多的注意. 如函数（Function：功能、运行），所以函数f（x）一般以首字母f表示;直线（Line），所以直线一般用l表示;曲线（Curve）以C表示，等等. 当多于一个数学对象的表示时，一般以原始对象的后续字母表示，如函数f（x），g（x），h（x）;直线l，m，n;曲线C，D，E. 这种数学语言的世界性标注规则，是对数学宽广文化背景的诠释，让学生从文化的角度认识数学语言的科学性和规范性.

②偶尔的一句中文词义标注，常常可以引起对概念更深層的思考. 如对函数概念的认识，“函”指容纳或者用匣子或封套装盛的意思，那么“函数”就是容纳实数或者把实数用匣子或封套装盛起来，这里的匣子或封套可以理解为集合. 这也从另一个侧面了解“函数”这一名称的用意. 再如很多学生对平均数和期望的概念没有一个正确的区分，教学时通过对期望的本意解释（对未来情况寄托希望或有所等待），让学生认识到期望有着对未来的一种坚定的向往. 所以不管随机变量在实验中的取值如何，都不会改变其值，它是随机变量取值想要达到的某种程度，是随机变量的本质属性. 而平均数只要到实验结束之后，便可知，其值会随实验的不同而变化，是随机变量的外在表现形式.

2. 数学符号的文化渊源

数学符号是数学思维的表现形式，它能清晰地表达出数学思维的过程，是数学思维的载体. 人们在长期实践中，由于研究的需要，创造了大量的数学符号，来代替或表示某些数学概念、运算与关系.

（1）数学符号的缩略记法.

符号的引入不是随意的，而是有客观依据的，是为了人们便于书写、理解、记忆和应用. 多数数学符号的产生，源于文字的缩写. 如虚数单位“i”是引用imaginary number（虚数）的第一个字母;积分符号“■”也是引用了Summation（求和法）的第一个字母;自然对数的符号是“Natura logarithm”的缩写，知道这一点就不可能写成“In”了. 在教学中引导学生正确理解数学符号的含义，让学生意识到这些记号是约定俗成的，不可随意更改.

（2）数学符号的会意表达.

象形和会意也是数学符号的一个重要来源，数学符号语言有一种提示的功能，见其形，明其意. 在独立性检验中，学生对假说“H■”比较难以理解，不知道其传达的意思，其实“H”是Hypothesis （假设、假说）的首字母，“0表示没有”，两者连起来就是“假设没有关系”的意思，

（3）数学式子的直观印象.

数学式子的引入是科学的和自然的，直观的和形象的，如分数指数幂a■化为根式■，分子的m在根号内，分母n在根号外，不少学生容易把m，n换位了，我们可以用一个“子里母外”的俗语，其中隐含的意思不言而喻、心领神会，永久性地避免了错误的发生. 数学符号语言结构严谨，特征清晰，使用数学符号语言可以大大减少记忆量，从而使数学对象之间的结构关系表现得更清晰，更便于检索和联想.

■寻找数学思维的现实来源

1. 数学方法的生活灵感

（1）数学方法的形象比喻.

用学生生活中常见的现象来描述数学知识、原理或方法，使抽象的数学变得形象、生动而且易于掌握. 比如综合法证明过程就像生活中的“顺藤摘瓜”，只要“藤”不断，“瓜”一定能摘到. 这里的“藤”比喻为推理过程，“瓜”比喻为所证结论. 再如在教材（必修3）的随机抽样中，有这样一段话：“我们知道，为了判断一锅汤的味道如何，如果锅里的汤被充分搅拌了，那么我们只须尝一勺就可以了，同样的高质量的样本来自‘搅拌均匀的总体. ”对抽样方法的目的作出了形象的比喻.

在教学活动中，教师要针对教学内容，充分调动知识储备，合理发挥想象，注意事物彼此之间的关联、适当、适度的形象比喻，变抽象为具体，化呆板为生动，呈乏味为有趣. 例如，在综合法和分析法的具体教学中，我们可以把这种证明的过程比作从条件的此岸到结论的彼岸构建思维桥梁的过程. 我们知道，在现实生活中，建桥都是从两岸相对同时进行的. 所以证明也是从条件和结论同时出发，逐步向中心靠拢，实现对接.

（2）数学方法的经验启示.

许多数学思想和我们日常生活中遇到的一些简单道理是一致的，我们要把数学问题和这些日常生活中的简单道理联系起来，必修3的算法初步中，学生对于交换两个变量A和B的值的赋值语句“x=A，A=B，B=x”难以理解. 其实这一交换方法来自生活中的将两个容器中的溶液相互交换，如把两个容器中的酱油和醋相互交换. 要实现此目的，那么必须要借助一个空容器（即x），先把酱油倒入空容器（即x=A），再把醋倒入原先装酱油的容器（即A=B），最后把酱油倒入原先装醋的容器（即B=x）. 实践表明，在学生能够富有意义的原理、方法的抽象形式之前，具体的活动以及学生生活中熟知的知识和经验，能有效地帮助他们更好地理解数学知识方法的意义.

2. 数学构想的现实原形

（1）数学模型的生活反映.

数学模型是关于部分现实世界和为一种特殊目的而作的一个抽象的、简化的结构. 最经典的例子就是糖水不等式. 有两杯浓度不一样的糖水的浓度分别为■，■，且■<■，混合之后的濃度介于两者之间，即■<■<■. 它源自普通的生活灵感，却能推演出生活之外的客观规律，

（2）问题解决的日常举例.

学生在面对一个陌生的数学问题时，其思维总是自然而然地与日常思维接轨或相匹配，由此激活学生已有的活动体验，调动内部已经形成的经验、策略、模式，找到问题解决的突破.

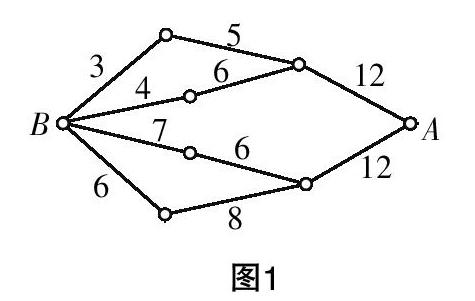
比如，小圆圈表示网络的结点，结点之间的连线表示它们有网线相连，连线标注的数字表示该段网线单位时间内可以通过的最大信息量. 现从结点A向结点B传递信息，信息可以分开沿不同的路线同时传递，则单位时间内传递的最大信息量为（  ）

A. 26 B. 24 C. 20 D. 19

这个问题比较陌生，如果把A看成是自来水总厂，B看成是某一用户的水龙头，那么从A分4路到达B，每一路线管中，水流量是由最细的管线所决定的，即是由每路管线中的每节管道的最大流量的最小值决定的，否则会使水管爆裂的，因此本题中的最大信息量为4条网线单位时间内可以通过的最大信息量的最小值之和.

■结语

生活孕育了数学，生活教会了数学，数学又服务于生活，生活和数学就像一对母子. 作为数学教育工作者，不能忽略数学遗传的各种生活性状，只有认识到数学寓于的生活道理，才能谈得上有意义的数学应用.