淤地坝蓄水加固改造方案的渗流和稳定性分析

王亮 聂兴山 郝瑞霞

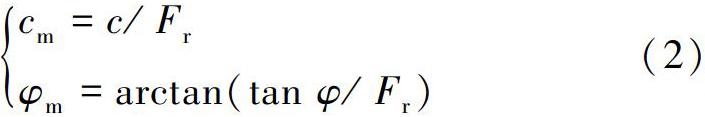
摘 要：为对淤地坝进行蓄水加固改造，基于流固耦合理论和强度折减法，应用ABAQUS有限元软件，对贺家庄淤地坝蓄水运行进行了渗流和稳定性分析，提出了黏土斜墙、土工膜等防渗改造思路，计算分析了各改造方案的稳定性和渗流特性。结果表明：采用的数值模拟方法与常用的传统方法比较是可行的;贺家庄骨干淤地坝作为水土保持工程措施，原设计不考虑长期蓄水，若按设计标准正常蓄水，其稳定性不满足要求，需进行加固改造，且仅使用上游坝坡放缓的方式很难达到预期的效果;土工膜改造方案和黏土防渗斜墙改造方案均能提升坝体安全系数、降低浸润线位置和减少渗透量;在原坝体上游坡铺设土工膜方案和铺设厚度为3 m的黏土斜墙均能满足稳定性要求。

关键词：淤地坝;流固耦合理论;ABAQUS软件;防渗加固;渗流分析;稳定性分析

中图分类号：TV64 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.04.026

引用格式：王亮，聂兴山，郝瑞霞.淤地坝蓄水加固改造方案的渗流和稳定性分析[J].人民黄河，2021，43（4）：137-141.

Abstract： In order to impound and reinforce warping dams， based on the fluid solid coupling theory and strength reduction method， this paper analyzed the seepage and stability of Hejiazhuang warping dam during its impoundment operation by using ABAQUS finite element software， put forward the ideas of seepage prevention and reconstruction such as clay inclined wall and geomembrane and calculated and analyzed the stability and seepage characteristics of each reconstruction scheme. The results show that： the numerical simulation method used in this paper is feasible compared with traditional methods; as a water and soil conservation measure， Hejiazhuang main warping dam did not consider long-term water storage in the original design. If the water storage is normal according to the design standard， its stability does not meet the requirements， so it needs to be reinforced and reconstructed， and it is difficult to achieve the expected effect only by using the way of upstream dam slope slowing down; both the geomembrane reconstruction scheme and the clay inclined wall reconstruction scheme can improve the safety coefficient of dam body and reduce the position of phreatic line and reduce the seepage; the scheme of laying geomembrane on the upstream slope of the original dam body and the laying of clay inclined wall with the thickness of 3 m can meet the stability requirements.

Key words： warping dam; fluid-solid coupling theory; ABAQUS; seepage prevention and reinforcement; seepage analysis; stability analysis

黃土高原地区传统淤地坝作为一项水土保持工程措施，在建造时没有采取防渗措施，不具备长期蓄水的功能。为了应对山西省水资源短缺的现状，对过去建设的大量淤地坝提出了蓄水加固改造的思路[1-2]，而淤地坝蓄水运行加固改造的关键技术问题是坝体的防渗和稳定性。

早期，受计算工具的限制，渗流分析主要采用流网法、电模拟试验法等，边坡稳定分析常使用极限平衡法。随着计算机技术的发展，数值分析方法逐渐成为渗流和稳定性计算的主要方法[3]。在土坝渗流作用下进行稳定分析时，一般将渗流场和应力场视为两个互不影响的场分别进行计算分析，黄茂松、毛昶熙等[4-5]使用有限元法对坝坡进行渗流计算，将计算结果作为初始条件，再进行稳定计算。实际上，坝体的渗流场和应力场并不是单独作用的，渗流场的渗流体积力和渗透压力会以外荷载的方式作用于坝体，改变坝体应力场，而应力场的变化会通过改变土体孔隙率和渗透系数来影响渗流场[6-7]。

随着有限元法的发展，土坝在渗流作用下的稳定计算愈加符合实际情况。20世纪中期，Biot[8]以有效应力理论为基础，建立了土体三维固结理论，为孔隙介质流固耦合研究奠定了基础;在此基础上柴军瑞、陈晓平等[9-10]以均质土体的渗透特性为基础，提出了渗流场和应力场耦合分析的数学模型，进行了解法讨论，并建立了相应的非线性流固耦合分析模型;针对边坡、隧道和基坑开挖等工程，李宗坤、Asadollahi、平扬等[11-13]使用有限元法对其进行流固耦合分析，验证了流固耦合分析的合理性。

本文在考虑渗流场与应力场耦合的基础上，利用强度折减的有限元法对贺家庄骨干淤地坝进行渗流和稳定性分析。根据工程实际情况，提出了改造措施和方案，并分析了各方案对坝体渗流和稳定性的影响。

1 计算原理

1.1 流固耦合计算原理

对于淤地坝来说，由上下游水位差形成的水压力通过透水介质以渗透体积力的形式作用于土体，其大小和分布规律将直接影响应力场和位移场;坝体应力场的改变，使岩土介质产生压缩变形和固结，导致土体孔隙比发生变化，从而改变土体的渗透系数。ABAQUS软件通过建立以应力场和渗流场为未知量的数学模型来实现流固耦合分析。应力场和渗流场耦合有限元模型的矩阵形式[11]为

渗流边界条件提供水头，应力边界条件提供外荷载，变化的渗透系数由水-土特征曲线确定，以各土体单元节点的位移和孔隙水压力为未知量进行求解。

1.2 强度折减法基本原理

在理想弹塑性有限元计算中，常使用强度折减法得到边坡稳定安全系数，基本原理：将土体抗剪强度参数黏聚力c和内摩擦角φ按式（2）进行折减，得到新的黏聚力cm、内摩擦角φm并用于边坡稳定计算，通过不断增大折减系数Fr，直至土坡达到临界破坏状态，对应的折减系数Fr即为边坡稳定安全系数。

1.3 本构模型

有限元强度折减法常使用岩土材料中的理想弹塑性模型，如Mohr-Coulomb模型和Drucker-Prager模型，这两种模型各有特点，Mohr-Coulomb模型计算稳定可靠，能描述岩土材料的屈服特性[14]。本文使用Mohr-Coulomb模型进行计算。

2 模型设置及验证分析

2.1 工程概况

贺家庄骨干淤地坝工程位于山西省运城市郑沟流域中游。该坝坝型为均质碾压土坝，筑坝材料为中轻粉质壤土。大坝高23.0 m，坝顶高程为453.0 m，坝顶宽为4.0 m，坝顶长为110.0 m，上游边坡1∶2.5，下游边坡1∶2、1∶1.5，下游马道在坝高12 m处、宽1.5 m，工程等级为5级。坝体剖面见图1，工程平面布置见图2。上游校核洪水位为450 m，在该工况下上游水深20 m，下游校核洪水位为430 m，在该工况下下游水深0 m。总库容为59.4万m3。上下游均采取植物护坡。

2.2 模型设置

考虑到坝基对渗流和应力稳定分析的影响，上下游各设置50 m长、20 m深的坝基作为计算区域。坝基底部约束水平和竖向位移，坝基两侧约束水平位移，上下游坝坡、河道和坝基两侧均为透水边界;模型整体施加重力荷载，上游坝坡施加静水荷载及等效的孔隙水压力;模型整体设置初始饱和度为1。本文使用CPE4P四节点平面应变四边形单元，原坝体计算模型共剖分139 208个单元、140 353个节点;当上游坝坡有材料分层时，对其进行网格细化，局部细化网格见图3。

土工膜厚度通常为毫米级别的，在数值模拟中很难对其进行建模计算。毛昶熙、介玉新等[15-16]提出土工膜在数值模拟中可按当量渗透系数来处理，即把很薄的土工膜等效为有一定渗透系数且厚度较大的材料。根据土工膜防渗效果等效原则，要求土工膜在主要防渗方向（厚度方向）上满足下式：

实验室中通过渗透试验测得的土工膜渗透系数一般为1×（10-13～10-15）m/s，本文取0.5 mm厚的土工膜，其渗透系数为1×10-14 m/s，等效厚度为3 m，等效渗透系数为1.0×10-10 m/s。

模型各部位材料参数见表1。

2.3 模型验证

对原坝体进行流固耦合分析，强度折减法通常有三种失稳判据：①在给定的迭代次数及特定限值条件下，计算不能满足所要求的收敛条件，则认为坝体失稳;②绘制模型内某一特征节点的位移与折减系数的关系曲线，当关系曲线出现明显拐点，即该特征节点位移突然增大，则认为坝体失稳;③当模型内的等效塑性区域贯通坝体时，则认为坝体失稳。本文采用被大多数学者使用的第一种判據，得到原坝体安全系数为1.080。同时采用瑞典圆弧法和简化Bishop法计算得到的原坝体安全系数分别是1.060和1.068，可以看出流固耦合法计算的安全系数大于极限平衡法所得安全系数，但相差仅1%～2%，该结论与其他研究者所得结论[14-17]一致。图4为使用流固耦合方法和水力学两段线法得到的坝体浸润线，流固耦合方法所得渗流逸出点高度较水力学两段线法的高2%，两种方法计算所得浸润线位置基本一致，证明本文使用流固耦合方法对坝体进行渗流和稳定性分析是可行的。

3 改造思路及方案

在蓄水状态下，原坝体安全系数不满足规范要求，易发生失稳破坏，需要进行加固防渗改造，而该坝下游有大面积耕地不宜占用，故以改造上游坝坡为主。贺家庄骨干淤地坝附近的土壤以红黏土为主，将红黏土作为防渗斜墙材料时，其渗透系数可达到1×10-9 m/s。土工膜作为近些年来被国内外广泛采用的防渗材料，具有防渗性能好、造价低廉、施工方便快捷等优点。因此本文防渗改造思路主要为三点，一是放缓上游坝坡;二是在上游坝坡铺设黏土防渗斜墙;三是在上游坝坡铺设复合土工膜，复合土工膜规格为两布一膜（250 g/m2）。其中放缓上游坝坡设置边坡系数分别为2.75和3.00两种方案;上游坝坡铺设黏土斜墙设置上游边坡系数m分别为2.50、2.75和3.00三种方案。改造示意见图5。

黏土斜墙防渗方案的上游坝坡从上至下依次为：30 cm厚干砌石护坡、50 cm保护层、3 m厚黏土斜墙（指水面处垂直厚度，各方案稍有不同）、20 cm厚垫层。复合土工膜防渗方案依次为：30 cm厚干砌石护坡、50 cm保护层、复合土工膜、20 cm厚垫层，下游坝坡维持不变。各防渗方案设置见表2。

4 计算结果和分析

各方案渗流和稳定计算结果见表3。典型方案B1和C1的浸润线与原坝体的对比见图6。

典型方案B1和C1临界破坏状态塑性应变见图7。

计算结果表明：

（1）当放缓上游坡时，随着上游坡度的变缓，渗径随之延长，渗流溢出点高度逐渐降低，单宽渗流量逐渐减小，与原坝体相比，方案A1、A2的渗流溢出点高度分别降低0.58%、1.95%，单宽渗流量分别减小1.95%、4.06%;方案A1、A2安全系数分别为1.083、1.091，均小于规范要求的1.15，渗流溢出点水力坡降分别为0.69、0.55，均大于允许水力坡降0.5，改造效果不明显。

（2）黏土斜墙防渗方案可以有效地降低水流进入原坝体的入渗点高度，从而降低浸润线，减小渗流量，增强坝体稳定性，与原坝体相比，方案B1、B2和B3的渗流溢出点高度分别降低69.53%、74.82%和76.47%，单宽渗流量分别减小69.77%、73.95%和76.74%，安全系数分别增大34.63%、38.52%和39.35%，3个方案的渗流溢出点水力坡降和安全系数均满足渗流安全和坝体稳定要求。随着黏土斜墙底部水平厚度的增加，方案B1、B2、B3的渗流溢出点高度和单宽渗流量也逐渐减小，但整体上变化幅度逐渐减少。

（3）复合土工膜防渗性能好，能够有效地减小渗透量、降低浸润线，与原坝体相比，采用复合土工膜防渗的方案C1渗流溢出点高度降低93.37%，单宽渗流量减小92.23%，安全系数增大57.69%，渗流出口水力坡降为0.11，小于允许水力坡降。

（4）在坝体失稳破坏过程中，塑性应变最先发生在坝基中部，随着破坏程度的加深，塑性应变区域延伸至坝体，最终临界破坏状态下，形成由坝脚至上游坝顶处的类圆弧状的塑性应变区域。原坝体及方案A1、A2的临界破坏状态塑性应变仅发生在坝体区域，而方案B1、B2、B3和C1的临界破坏状态的塑性应变区域会延伸至坝基2～3 m深处，说明部分坝基参与了整体抗滑，提高了坝体稳定性，所以黏土斜墙防渗方案和复合土工膜防渗方案的安全系数值也相应更大。

5 结 论

本文使用流固耦合方法对贺家庄淤地坝蓄水加固改造方案进行渗流和稳定性分析，并对各改造方案效果进行比较，得到如下结论：

（1）采用流固耦合方法，对改造前蓄水情况下贺家庄淤地坝进行渗流和稳定性分析，所得安全系数与使用极限平衡法得到的安全系数相差1%～2%，浸润线位置与传统水力学方法得到的结果十分接近，渗流逸出点高度相差2%，验证了本文所使用的流固耦合模型计算结果的可靠性。

（2）贺家庄淤地坝若按设计标准正常蓄水，其渗流安全和坝体稳定性均不满足要求，需要进行防渗加固改造，而仅使用放缓上游坝坡的措施很难满足正常蓄水要求。

（3）对贺家庄淤地坝上游坝坡采用黏土斜墙进行防渗，与改造前相比，改造方案B1、B2、B3渗流逸出点高度

降低63%～75%，单宽渗流量减少63%～73%，坝体安全系数提高31%～37%，均能满足渗透和稳定性的规范要求，但方案B1工程量最小。

（4）采用复合土工膜进行防渗改造，能使渗流逸出点高度

降低93.37%、单宽渗流量减少92.23%、坝体安全系数提高57.69%。与方案B1比较，其防渗效果更好些。

（5）经分析，在原坝体上游坡铺设土工膜方案和铺设厚度为3 m的黏土斜墙方案均是可行的。从防渗效果上考虑，铺设土工膜方案更优。具体采用哪种方法需结合当地材料、经济等因素综合考虑。

参考文献：

[1] 刘卉芳，曹文洪，秦伟，等.淤地坝在流域水土保持措施中的贡献研究[J].中国农村水利水电，2011（1）：55-58，64.

[2] 谷黎明，郝瑞霞.基于Autobank的苏家庄淤地坝防渗改造及渗流分析[J].水电能源科学，2019，37（7）：58-61.

[3] 李广信.高等土力学[M].北京：清华大学出版社，2004：114，182.

[4] 黄茂松，贾苍琴.考虑非饱和非稳定渗流的土坡稳定分析[J].岩土工程学报，2006，28（2）：202-206.

[5] 毛昶熙，陈平，李祖贻，等.渗流作用下的坝坡稳定有限单元分析[J].岩土工程学报，1982，4（3）：87-106.

[6] 张延军，王恩志，王思敬.非饱和土中的流-固耦合研究[J].岩土力学，2004，25（6）：999-1004.

[7] 郑立夫，高永涛，周喻，等.基于流固耦合理论水下隧道冻结壁厚度优化研究[J].岩土力學，2020，41（3）：1-11.

[8] BIOT M A . General Theory of Three Dimensional Consolidation[J]. Journal of Applied Physics， 1941， 12（2）：155-164.

[9] 柴军瑞，仵彦卿.均质土坝渗流场与应力场耦合分析的数学模型[J].陕西水力发电，1997，13（3）：4-7.

[10] 陈晓平，茜平一，梁志松，等.非均质土坝稳定性的渗流场和应力场耦合分析[J].岩土力学，2004，25（6）：860-864.

[11] 李宗坤，陈丽刚，韩立炜.基于ABAQUS渗流与应力耦合的边坡稳定性分析[J].人民黄河，2011，33（2）：103-104.

[12] ASADOLLAHI P，TONON F. Constitutive Model for Rock Fractures： Revisiting Barton's Empirical Model[J]. Engineering Geology， 2010，113（1）：11-32.

[13] 平扬，白世伟，徐燕萍.深基坑工程渗流-应力耦合分析数值模拟研究[J].岩土力学，2001，22（1）：37-41.

[14] 张晓咏，戴自航.应用ABAQUS程序进行渗流作用下边坡稳定分析[J].岩石力学与工程学报，2010，29（增刊1）：2927-2934.

[15] 毛昶熙，段祥宝，李祖贻，等.渗流数值计算与程序应用[M].南京：河海大学出版社，1999：22-24.

[16] 介玉新，李广信.有限元计算中土工合成材料渗流问题的处理[J].水利水电科技进展，2009，29（6）：42-43，62.

[17] 王宏权，裴广龙，刘夫江，等.基于ABAQUS强度折减法的边坡安全系数敏感性研究[J].三峡大学学报（自然科学版），2014，36（6）：43-46.

【责任编辑 赵宏伟】