Redefined Extended Cubic B-Spline Functions for Numerical Solution of Time-Fractional Telegraph Equation
2021-04-27MuhammadAminMuhammadAbbasDumitruBaleanuMuhammadKashifIqbalandMuhammadBilalRiaz
Muhammad Amin,Muhammad Abbas,Dumitru Baleanu,Muhammad Kashif Iqbal and Muhammad Bilal Riaz
1Department of Mathematics,National College of Business Administration&Economics,Lahore,54660,Pakistan
2Department of Mathematics,University of Sargodha,Sargodha,40100,Pakistan
3Department of Mathematics,Faculty of Arts and Sciences,Cankaya University,Ankara,06530,Turkey
4Department of Medical Research,China Medical University Hospital,China Medical University,Taichung,40402,Taiwan
5Institute of Space-Sciences,Bucharest,077125,Romania
6Department of Mathematics,Government College University,Faisalabad,38000,Pakistan
7Department of Mathematics,University of Management and Technology,Lahore,54700,Pakistan
ABSTRACT This work is concerned with the application of a redefined set of extended uniform cubic B-spline (RECBS)functions for the numerical treatment of time-fractional Telegraph equation.The presented technique engages finite difference formulation for discretizing the Caputo time-fractional derivatives and RECBS functions to interpolate the solution curve along the spatial grid.Stability analysis of the scheme is provided to ensure that the errors do not amplify during the execution of the numerical procedure.The derivation of uniform convergence has also been presented.Some computational experiments are executed to verify the theoretical considerations.Numerical results are compared with the existing schemes and it is concluded that the present scheme returns superior outcomes on the topic.
KEYWORDS Extended cubic B-spline;redefined extended cubic B-spline;time fractional telegraph equation;caputo fractional derivative;finite difference method;convergence
1 Introduction
In recent years,fractional calculus has gained a remarkable importance.Fractional derivatives and integrals have manifold applications in science and engineering such as fluid mechanics,chemical physics,electricity,control theory,biomedical,epidemic diseases,hydrology,electrochemistry,probability theory,signal processing,heat conduction and diffusion problems [1–7].Many researchers developed fractional-order models to describe real-world problems and studied their analytical and numerical solutions [8–11].These models involve different types of fractional derivative operators [12–15].The fractional telegraph equation is one of the fundamental mathematical models arising in the study of electrical signals in transmission line and wave phenomena [16–18].Basically,it belongs to the family of hyperbolic partial differential equations.Several numerical and analytical techniques have been proposed for solving these type of equations.In [19],the authors employed Adomian decomposition method for solving time and space fractional telegraph equations.Dehghan et al.[20] proposed variational method to explore the series solution to multi space telegraph equation.The authors in [21],employed Homotopy analysis method to explore the analytical solution of telegraph equation involving fractional time derivative.Later on,Hayat et al.[22] used Homotopy perturbation technique to study time fractional telegraph equation.They handled TFTE for both brownian and standard motion.In [23],Wei et al.applied fully discrete local discontinuous Galerkin finite element method to solve fractional telegraph equation.Hosseini et al.[24] studied the numerical solution of fractional telegraph equation by means of radial basis functions.Srivastava et al.[25] employed reduced differential transformation method for second order hyperbolic time fractional telegraph equation in one dimensional space.Wang et al.[26] analyzed anH1-Galerkin mixed finite element method for the numerical solution of time fractional telegraph equation.Modanli et al.[27] solved fractional order telegraph equation by means of Theta method.Xu et al.[28] applied Legendre wavelets direct method for solving fractional order telegraph equation.In [29],Wang et al.utilized spectral Galerkin approximation to study the approximate solution of TFTE.Kamran et al.[30]studied the numerical solution of TFTE by means of a Localized kernal-based approach.Here,in this work,we consider the following fractional order telegraph equation.
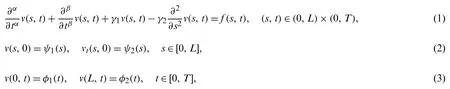
whereψj(s)andφj(t) (j=1,2)are given andrepresent the Caputo fractional derivatives of orderαandβ,respectively.It is worth mentioning that in (1),α∈(1,2] andβ∈(0,1].However,this work is restricted to the class of problems involvingα=β+1 andα=2β.
In this paper,we have studied the application of a redefined form of extended cubic B-spline(ECBS) functions for the numerical treatment of time-fractional Telegraph equation (TFTE).These functions are generalized forms of cubic B-spline functions involving one free shape parameter which provides the flexibility to modify the shape of the solution curve [31].Although,the degree of the piecewise polynomials is enhanced by one and the continuity of RECBS remains of order three.A finite-difference formula is used for the discretization of the Caputo time-fractional derivative.Usually,in collocation techniques,the Dirichlet’s type end conditions are imposed where the basis of spline functions vanish,but the typical ECBS functions do not vanish at boundaries.We have employed RECBS functions for spatial discretization,as these basis functions die out on the boundaries where the Dirichlet’s types of conditions are specified.The present approach is novel for the approximate solution of fractional PDEs and as far as we are aware,it has never been employed for this purpose before.
The manuscript is composed as:Section 2 describes the redefined extended cubic B-spline functions.In Section 3,the numerical method has been explained.In Section 4,the stability analysis of proposed method is presented.In Section 5,we have derived the results for theoretical convergence.The approximate results and discussion are reported in Section 6.Finally,the concluding remarks have been given in Section 7.
2 Redefined Extended Cubic B-Spline Functions
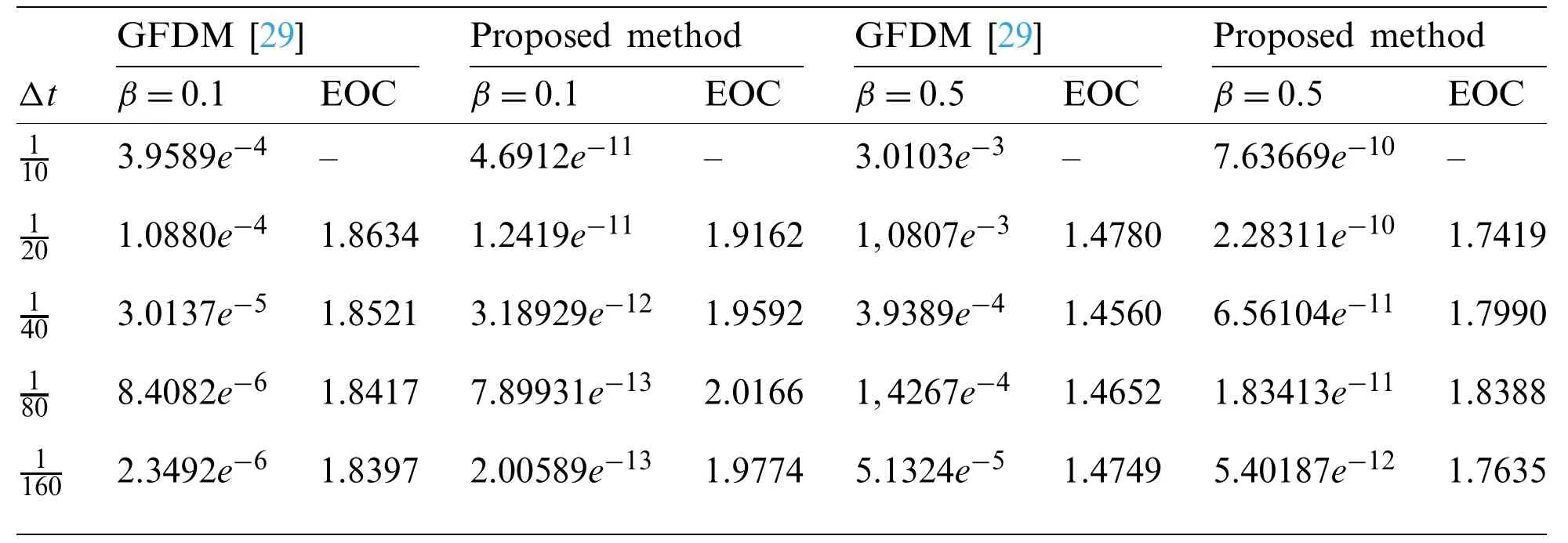
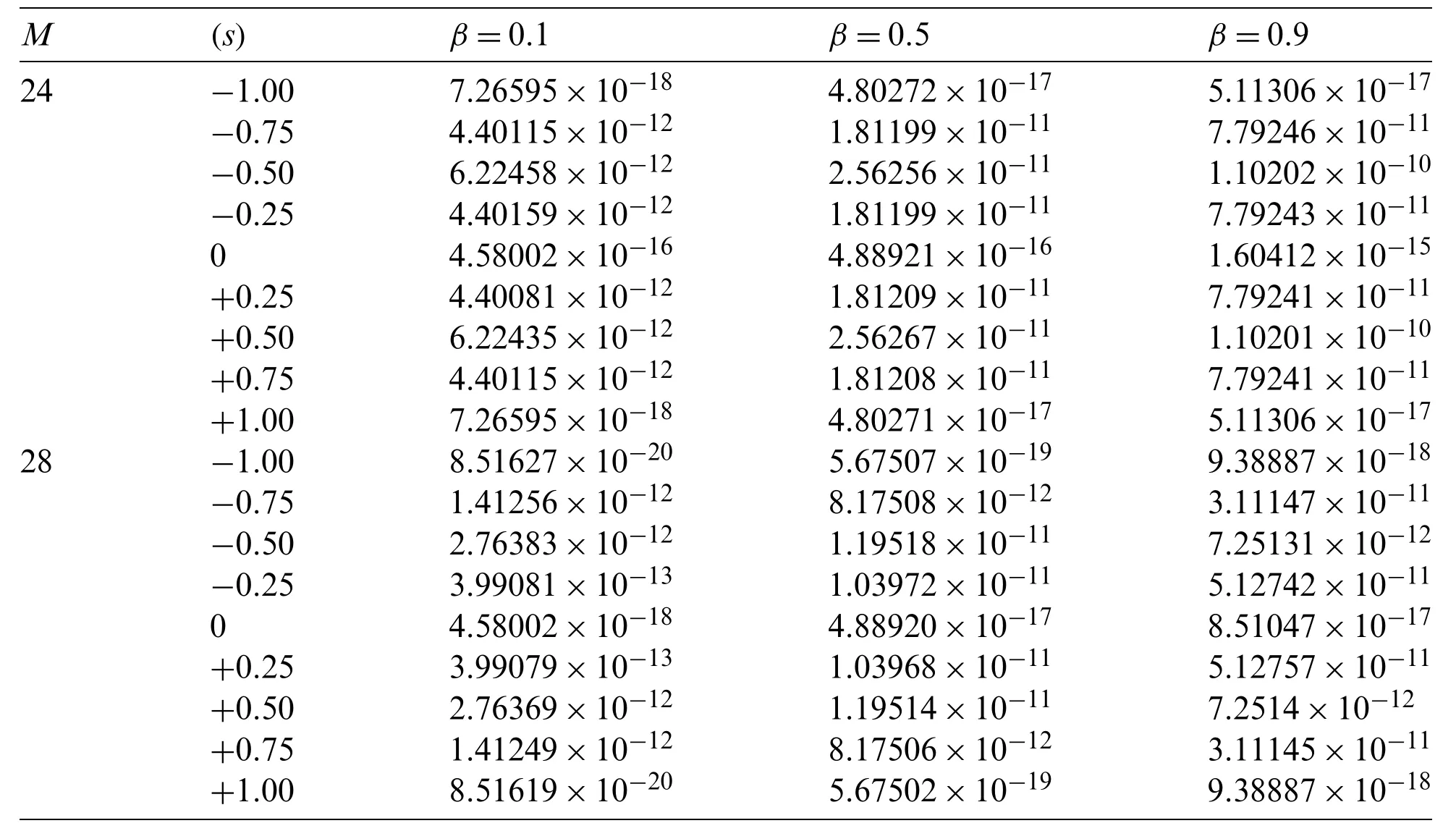
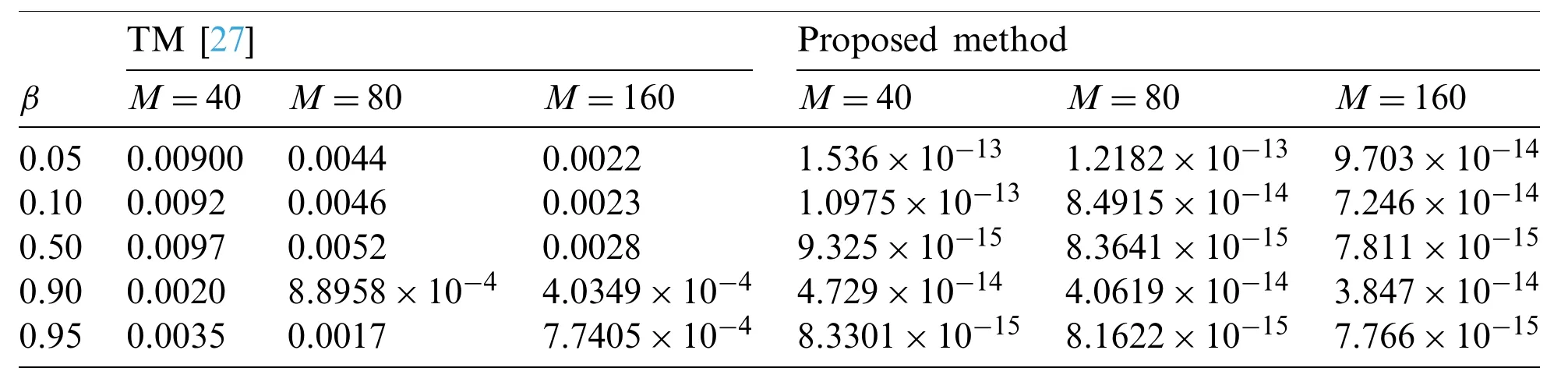
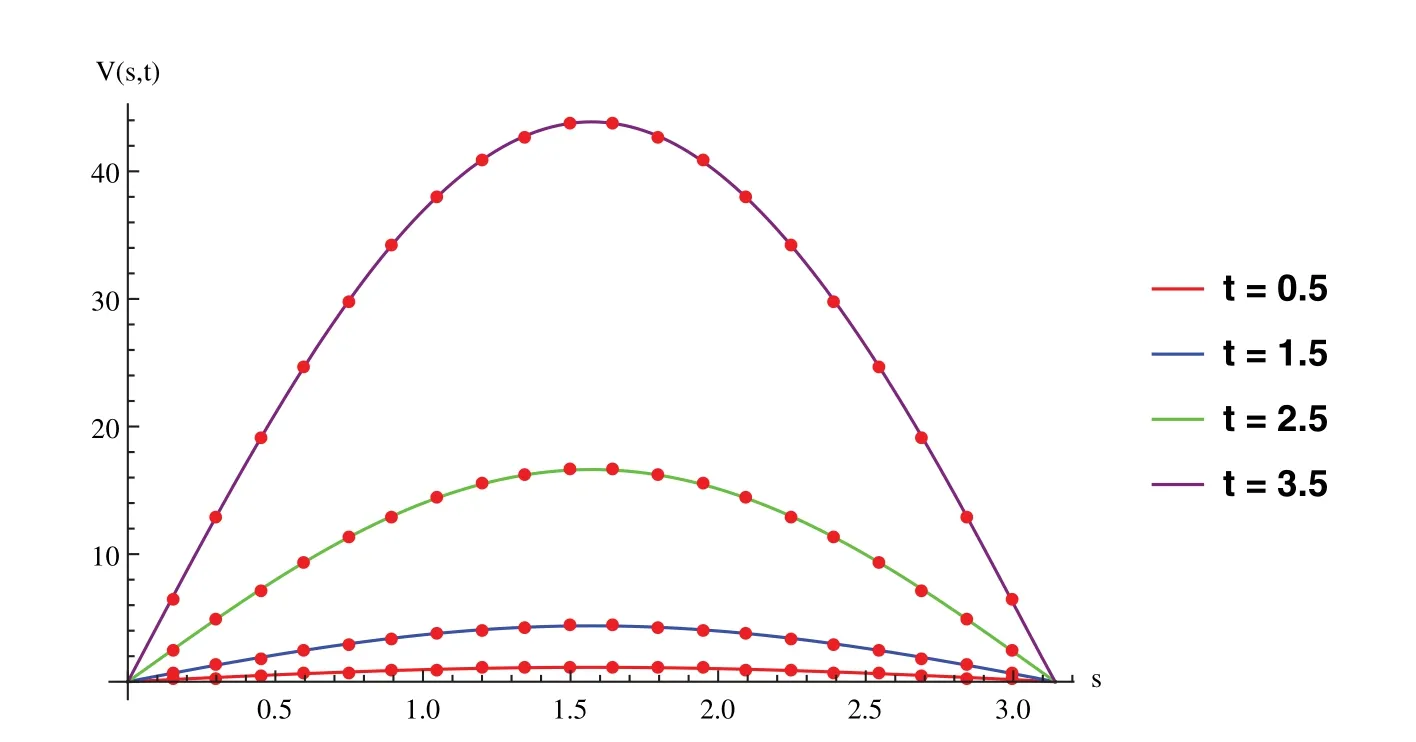
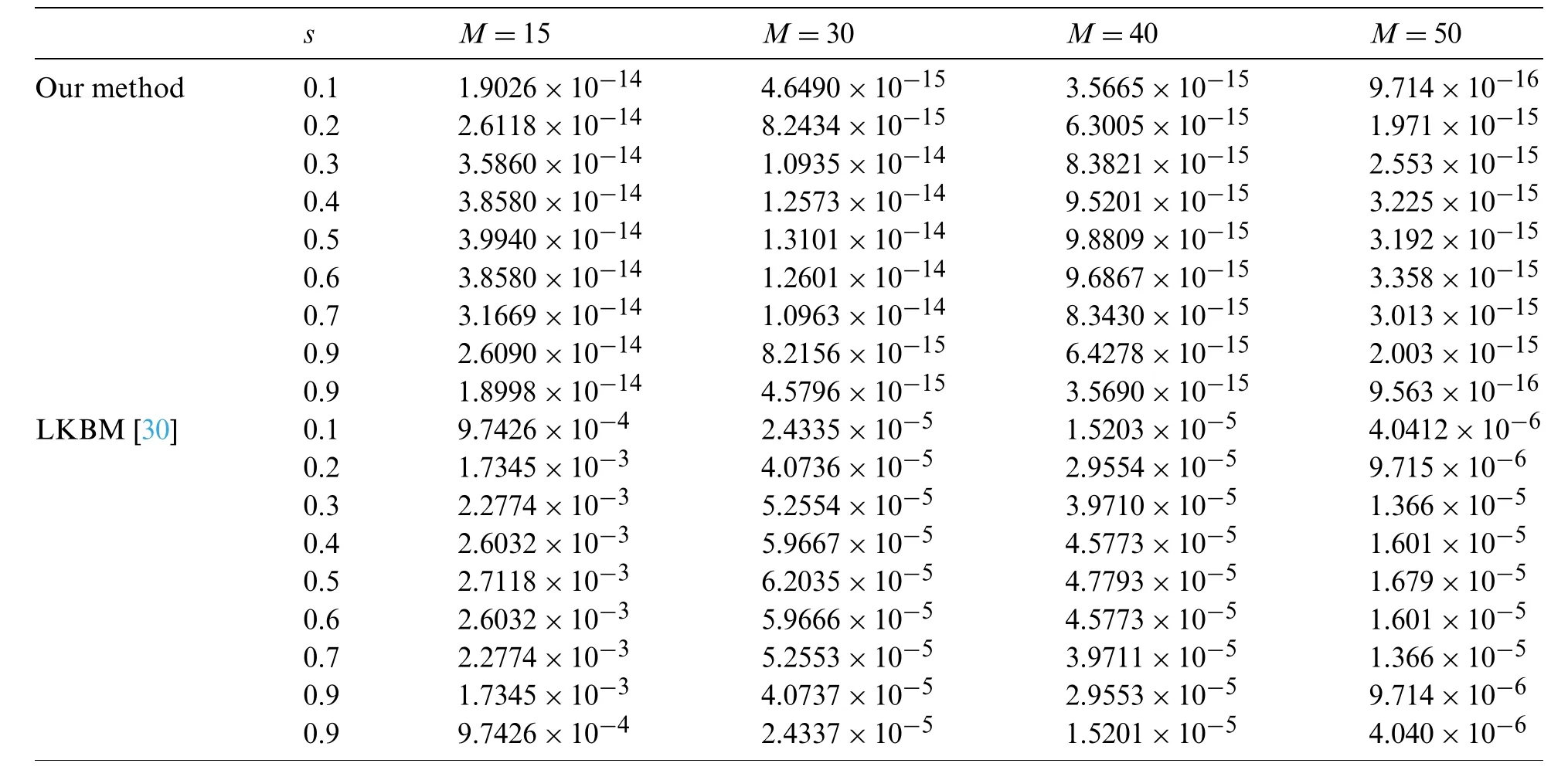
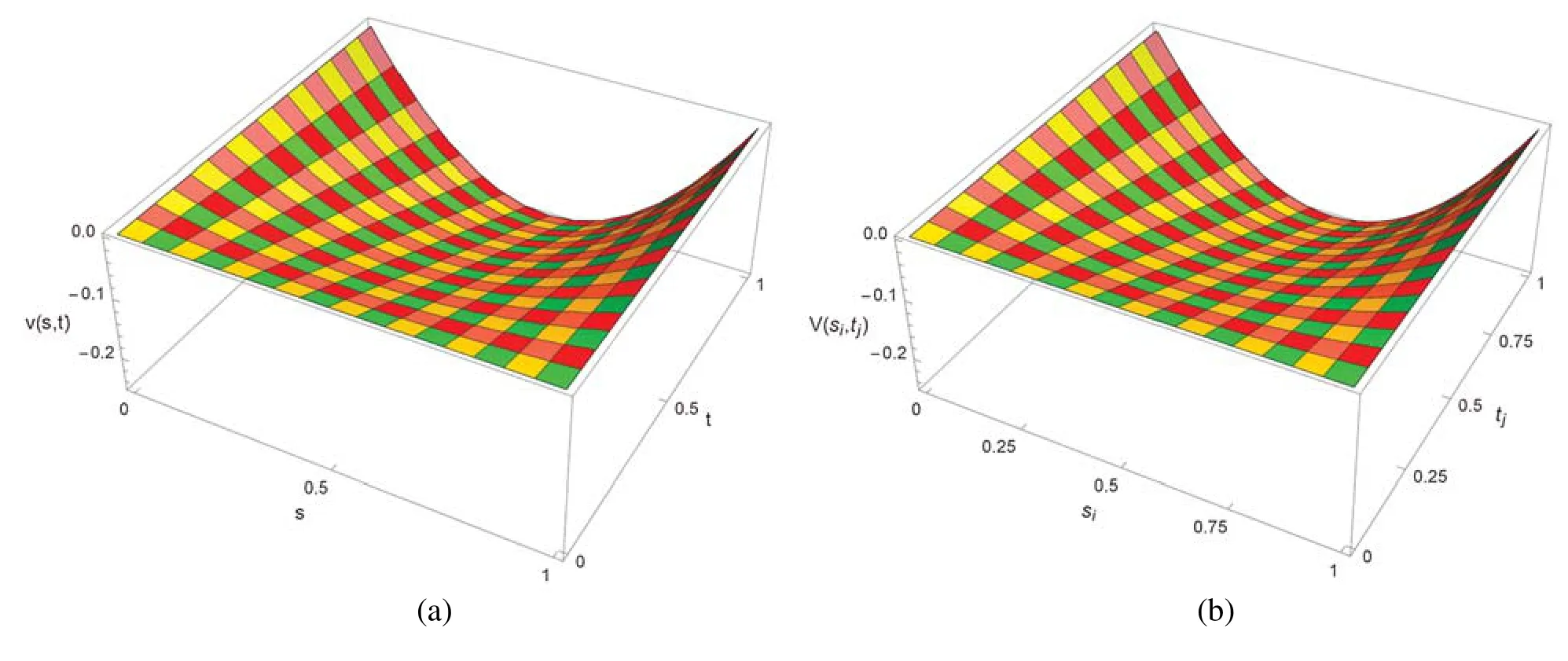
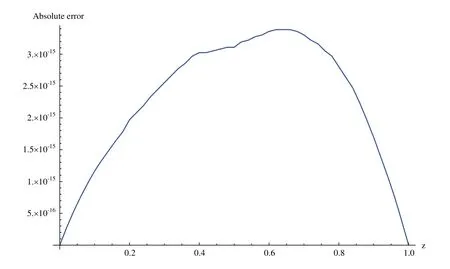
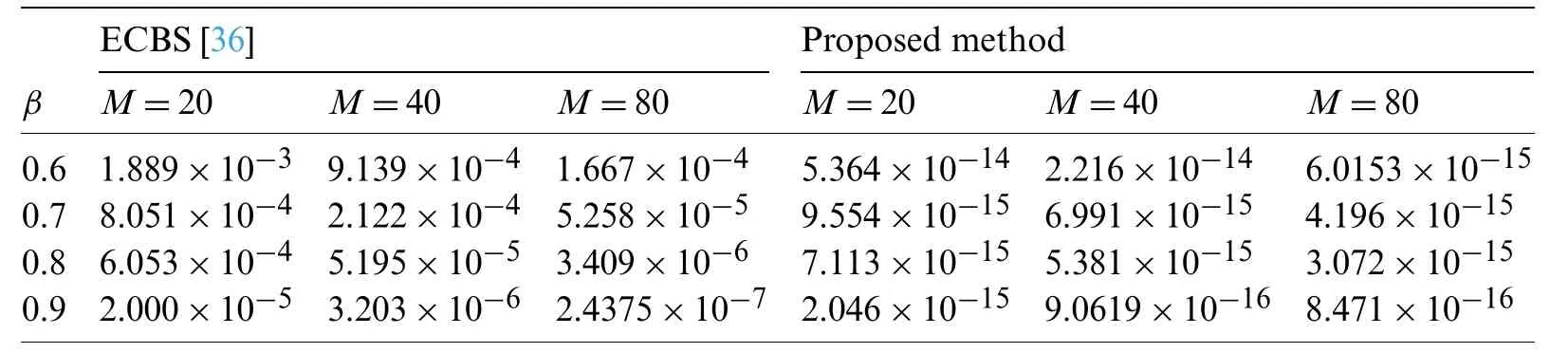
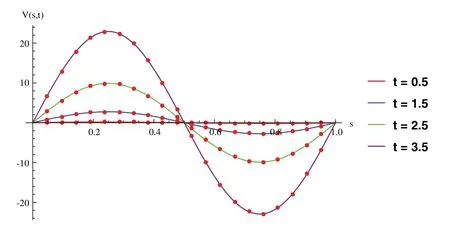
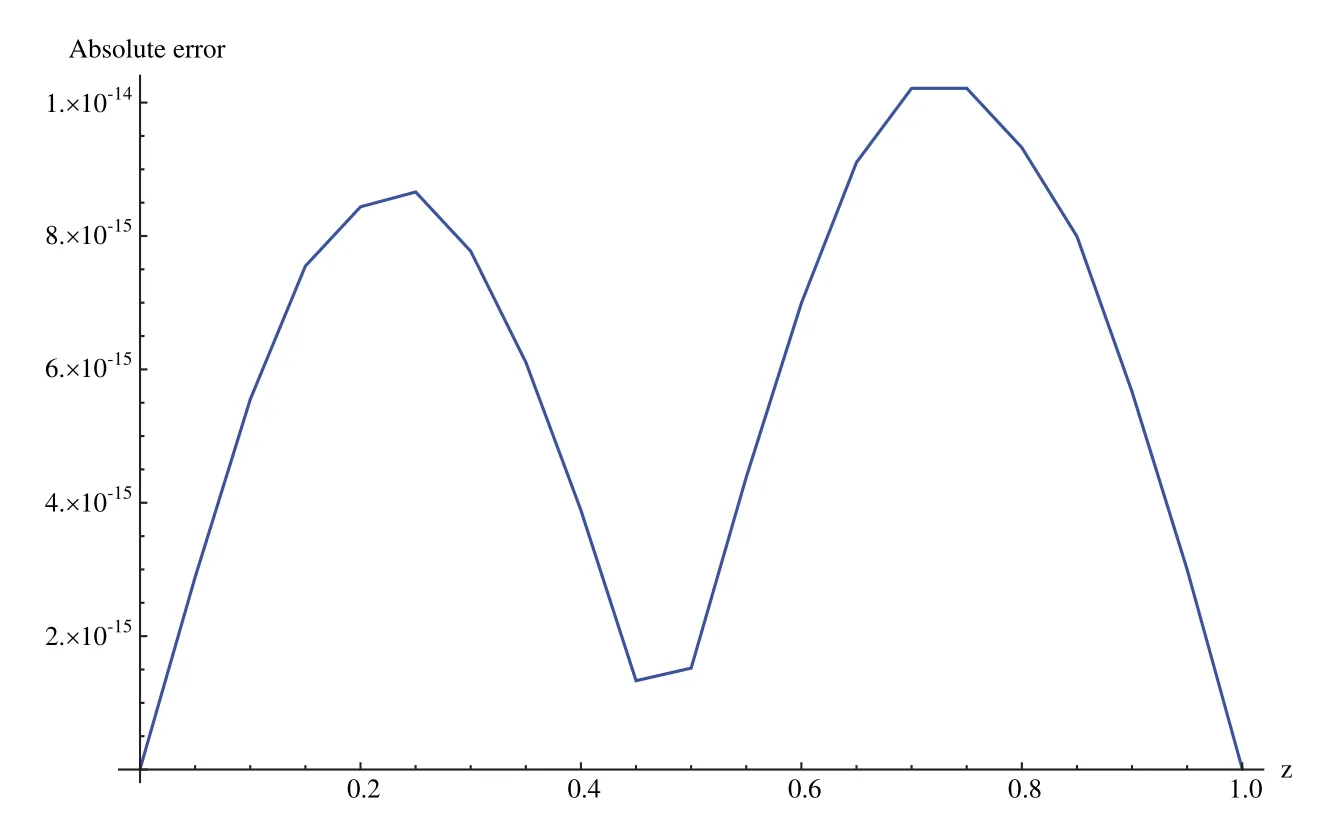
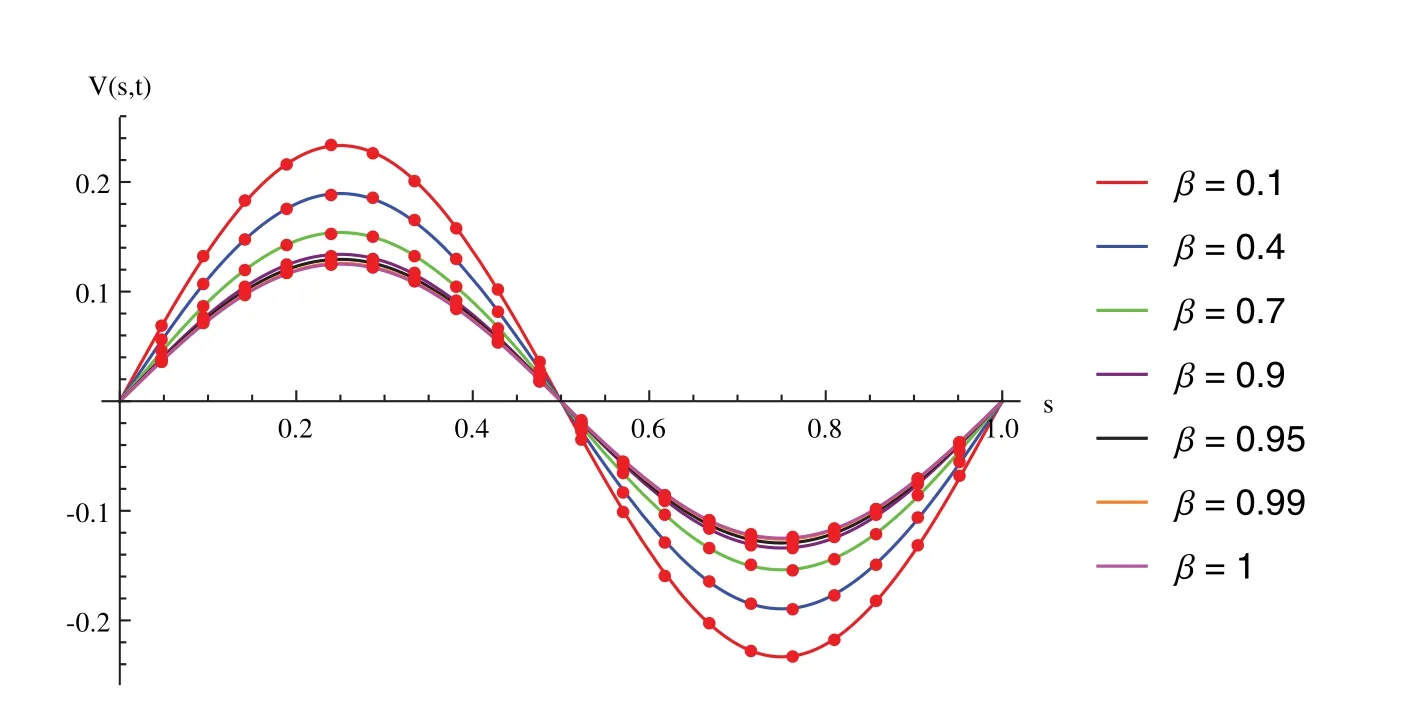
Suppose the spatial domain [a,b] be portioned intoMparts of equal lengthh=such thata=s0 whereξm(t)are real constants andλm(s,κ)are ECBS functions [32]: where−8 ≤κ≤1 is responsible for fine tuning the shape of the curve.The approximate solution(V∗)rm=V∗(sm,tr)and its first two derivatives with respect to space variables,atmth knot andrth time step,in terms ofξmcan be expressed as whereThe ECBS functionsλ−1,λ0,...,λM+1do not vanish at the boundaries when Dirichlet type end conditions are imposed.Therefore,we redefine these functions in such a manner that the resulting basis vanish at the boundaries [33].We eliminateandfrom Eq.(4) as where the weight functionΦ(s,t)and redefined ECBS (RECBS) functions are given by We divide the time domain [0,T] intoRsubintervals [tr,tr+1] s.t.tr=rΔt,r=0,1,2,...,RandΔt=.The Caputo’s time fractional derivative att=tr+1,forα∈(1,2],can be discretized as wherepj=(j+1)2−α−(j)2−α,υ=(tr+1−w)and(Eα)is the truncation error. Also whereρ1is constant and •pj∈Z+,∀j • 1=p0>p1>p2>p3>···>pr,pr→0 asr→∞ •(2p0−p1)++(2pr−pr−1)−pr=1 Similarly, whereqj=(j+1)1−β−(j)1−β,υ=(tr+1−w)and(Eβ)is the truncation error. Also whereρ2is constant and •qj∈Z+,∀j • 1=q0>q1>q2>q3>···>qr,qr→0 asr→∞ Substituting (10) and (12) in (1) att=tr+1,we get Using theta-weighted scheme forθ=1,Eq.(14) takes the following form where Forr=0,v−1appears in Eq.(15).We use the initial conditions and substitutev−1=v0−Δtψ2(s)to get the following equation Forr=1,2,...,R,Eq.(15) is reshaped as Now,we discretize the spatial domain [a,b] byM+1 equally spaced knotsa=s0,s1,s2,...,sM=bsuch thatsm=s0+mh,m=0,1,...,Mand assume that the RECBS approximationV(s,t)for the exact solutionv(s,t)is given by whereΦ(s,t)and(s,κ)are defined in (8) and (9),respectively. The initial solution is given in (2).However,the control pointsξiatt=t1are required to start the main scheme (17).For this purpose,(18) is substituted into (16) to get the following system of equations Using (18) in Eq.(17),we obtain Eq.(20) represents a set of(M+1)equations involving(M+1)unknowns.This system of equations is solved to forand their values are plugged into (18) to get the required solution at(r+1)th time level. We apply Fourier method to study the stability of our numerical method.Letanddenote the Fourier growth factor and its approximate value.We introduce the error termas whereUsing (21) in (20),the error equation at(r+1)st time level is given by If=εreινmh,whereι=andν=,then (22) is reshaped as After simplifying (23),we get the following result where Forr=0,the expression (23) takes the following form Now,assuming |εr|≤(1+η1)|ε0|forr>1,we use (24) to proceed as Consequently,following [34],we have Hence,the scheme stable. whereand The boundary conditions can be rewritten as Moreover,following [34],we have Now,we introduceandForr=0,Eq.(25) transforms into following relation Involving the absolute values ofand,we obtain Hence,employing the end constraints,we get≤F1h2,where F1is independent of spatial grid spacing. Utilizing the boundary conditions,we obtain≤Fh2. Hence,the last result is true for allr.Using the result[34],we get Consequently,using (26) and (27),we get Hence,in the light of above discussion together with (11) and (13),we conclude that the scheme isO(h2)accurate in spatial direction.However,(11) and (12) imply that the truncation error in temporal direction isO(Δt2−α+Δt1−β).This work is restricted to the class of problems involvingα=β+1 andα=2β.Therefore,theoretically the scheme isO(Δt2−α)whenα=1+βandO(Δt1−α/2)whenα=2β. To investigate the accuracy of presented technique,some numerical experiments are presented.For this purpose,following error norms have been used Also,the experimental order of convergence (EOC) is computed by following important formula [35]: Example 6.1.As the first experiment,we take the following multi term TFTE [29] whereα=β+1 and The exact solution of the problem isv(s,t)=t2sin(πs). The absolute error and temporal order of convergence for Example 6.1 along temporal direction usingM=24 and different values ofβare reported in Tab.1.It can easily be seen that our results are more accurate than the scheme based on generalized finite difference method(GFDM) [29].In Tab.2,we have computed the absolute errors by settingM=24,28 andΔt=0.1 corresponding to different grid points in spatial direction.Tab.3 gives spatial order of convergence(EOC) subject toβ=0.6 andΔt=0.1.The experimental rate of convergence of the current method is found to be in line with the theoretical appraisal.Fig.1 shows the physical behaviour of approximate solutions at different time levels whenβ=0.1,M=24 andΔt=0.1.The 3D visuals of exact and numerical solutions withβ=0.1,M=24 andΔt=0.1 are shown in Fig.2,whereas,Fig.3 depicts the absolute error between the exact and approximate solutions usingβ=0.1,M=36 andΔt=0.1. The piecewise defined approximate solution for Example 6.1 using proposed algorithm,whenβ=0.50,−1 ≤s≤1,M=20,Δt=0.01,is given by Example 6.2.Consider the TFTE [27] Table 1:Experimental order of convergence (EOC) for Example 6.1 when M=24 using different values of β Table 2:Absolute errors for Example 6.1 when Δt=0.1 using different values of β Table 3:Experimental order of convergence (EOC) for Example 6.1,when β=0.6 and Δt=0.1 whereα=2,0<β≤1 and Figure 1:Exact and numerical solution for Example 6.1 at different time levels when Δt=0.1,β=0.1 and M=24 Figure 2:Exact and approximate solution for Example 6.1 with M=24,Δt=0.1 and β=0.1.(a) 3D plot for exact solution.(b) 3D plot for approximate solution Figure 3:Absolute error for Example 6.1 when M=36,β=0.1 and Δt=0.1 The analytical solution to this problem is sin(s)(t3+1). The approximate analytical solution for Example 6.2 using proposed method,whenβ=0.50,0 ≤s≤π,M=20 andΔt=0.01 is given by The absolute numerical errors in RECBS solution for Example 6.2 settingΔt=hat different values ofβare listed in Tab.4.It is clear that our results have better agreement with the exact solution in comparison to the theta-method (TM) [27].Fig.4 shows the physical behaviour of approximate solutions at different time levels whenβ=0.5,M=40 andΔt=0.025.The 3D visuals of exact and numerical solutions withβ=0.5,M=40 andΔt=0.025 are shown in Fig.5.Whereas,Fig.6 depicts the absolute error between the exact and approximate solutions usingβ=0.75,M=40 andΔt=0.025. Table 4:Absolute error norms for Example 6.2 using different values of M and β Figure 4:Exact and numerical solution for Example 6.2 at different time levels when Δt=0.025,β=0.5 and M=40 Example 6.3Consider the multi term TFTE [30] whereβ=α−1 Figure 5:Exact and approximate solution for Example 6.2 with Δt=0.025,β=0.50 and M=40.(a) 3D plot for exact solution.(b) 3D plot for approximate solution Figure 6:Absolute error for Example 6.2 when M=40,β=0.75 and Δt=0.025 The exact solution is(s2−s)t. The numerical solution for Example 6.3,whenα=1.50,0 ≤s≤1,M=20,Δt=0.01 is given by The absolute numerical errors in RECBS solution to Example 6.3 usingΔt=0.1,α=1.95 corresponding to different grid points are listed in Tab.5.It is observed that our results are better than the localized kernel–based method (LKBM) [30].Fig.7 shows the physical behaviour of approximate solutions at different time levels whenα=1.5,M=100 andΔt=0.01.The 3D visuals of exact and numerical solutions withα=1.5,M=100 andΔt=0.01 are shown in Fig.8.Whereas,Fig.9 depicts the absolute error between the exact and approximate solutions usingα=1.5,M=100 andΔt=0.01. Table 5:Absolute error for Example 6.3 when Δt=0.1 for different values of s and α=1.95 Figure 7:Exact and numerical solution for Example 6.3 at different time levels when Δt=0.01,M=100 and α=1.5 Figure 8:Exact and approximate solution for Example 6.3 with M=100,Δt=0.01 and α=1.50.(a) 3D plot for exact solution.(b) 3D plot for approximate solution Example 6.4 whereα=2β, Figure 9:Absolute error for Example 6.3 when M=100,α=1.50 and Δt=0.01 The analytical solution ist2+βsin(2πs).The piecewise defined approximate solution for Example 6.4,whenβ=0.6,0 ≤s≤1,M=20,Δt=0.01 is given by The comparison ofL2−normfor Example 6.4 usingh=5,Δt=,(R=20,40,80)is reported in Tab.6.It is found that our proposed algorithm has better accuracy when compared to ECBSM [36].Tab.7 shows the comparison of the calculated values of the order of convergence with proposed method for different values of spatial grid pointsMusingβ=0.75 andΔt=0.01.Fig.10 shows the physical behaviour of numerical solutions at different time levels whenβ=0.5,M=40 andΔt=0.01.The 3D visuals of exact and numerical solutions withβ=0.5,M=40 andΔt=0.01 are shown in Fig.11,whereas,Fig.12 depicts the absolute error between the exact and approximate solutions usingβ=0.5,M=40 andΔt=0.01.Fig.13 represents the behaviour of solution curve for different values ofβ. Table 6:Absolute error norms for Example 6.4 using different values of M and β Table 7:Experimental order of convergence for Example 6.4 using different values of M and Δt=0.01 Figure 10:Exact and numerical solution for Example 6.4 at different time levels when Δt=0.01,β=0.5 and M=40 Figure 11:Exact and approximate solution for Example 6.4 with M=20,Δt=0.01 and β=0.5.(a) 3D plot for exact solution.(b) 3D plot for approximate solution Figure 12:Absolute error for Example 6.4 when M=20,β=0.5 and Δt=0.01 Figure 13:Exact and numerical solutions for Example 6.4 with different values of β This work is concluded with following remarks: 1.An efficient algorithm based on a redefined set extended basis splines is proposed for numerical solution of multi-term time-fractional telegraph equation. 2.The fractional time derivatives have been considered in the Caputo sense. 3.The finite difference formulae have been used to discretize time-fractional derivatives while the discretization of spatial derivatives has been achieved by means of redefined extended B-spline functions. 4.The spatial discretization used in this manuscript is superior to the other existing methods because the proposed method give continuous approximation with high accuracy to the solution curve of the unknown function and its derivatives at each and every point of the range of integration. 5.The stability of presented algorithm has been proved along temporal grid. 6.The theoretical results show that the accuracy of presented numerical approach in spatial direction is of orderO(h2)whereas in time direction it isO(Δt2−α)whenα=1+βandO(Δt1−α/2)whenα=2β. 7.The numerical rate of convergence is in the line with theoretical results. 8.The comparison of error norms reveals that in terms of accuracy and straightforward implementation,the proposed algorithm performs better than the methods in [27,29,30,36]. Acknowledgement:We thank Dr.Nauman Khalid,Govt Post Graduate College,Faisalabad,Pakistan for his assistance in proofreading the manuscript. Funding Statement:The author(s) received no specific funding for this study. Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
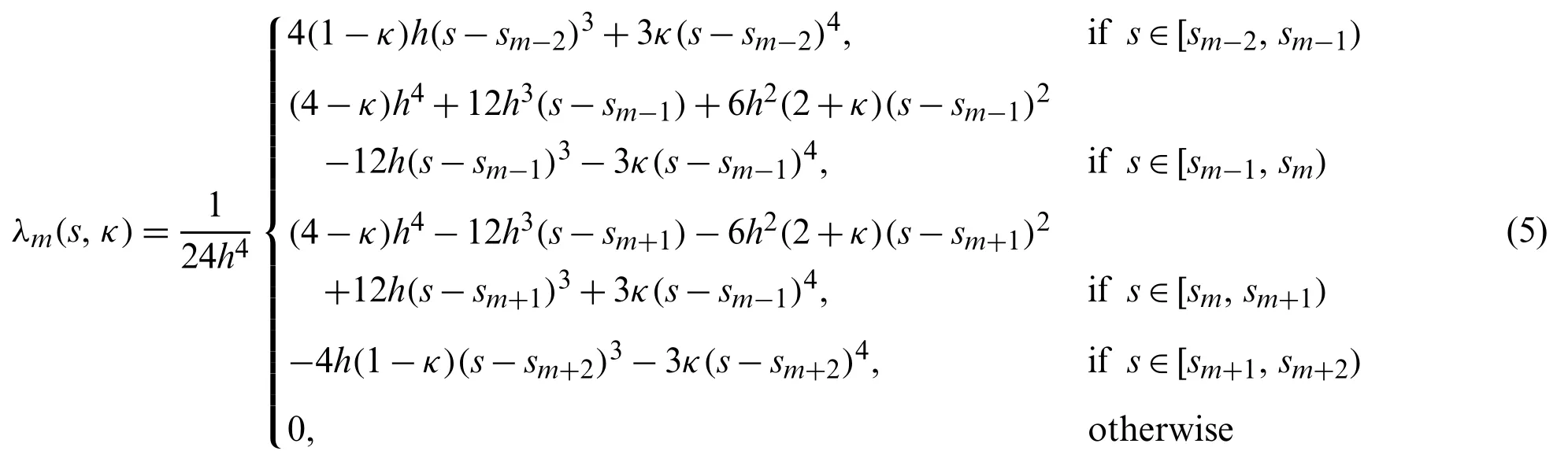



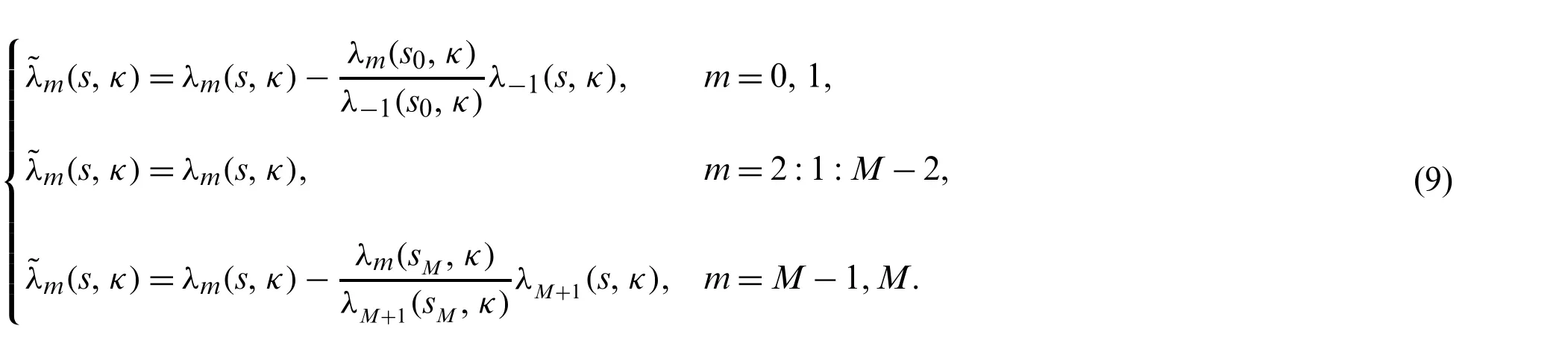
3 Numerical Technique




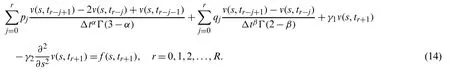
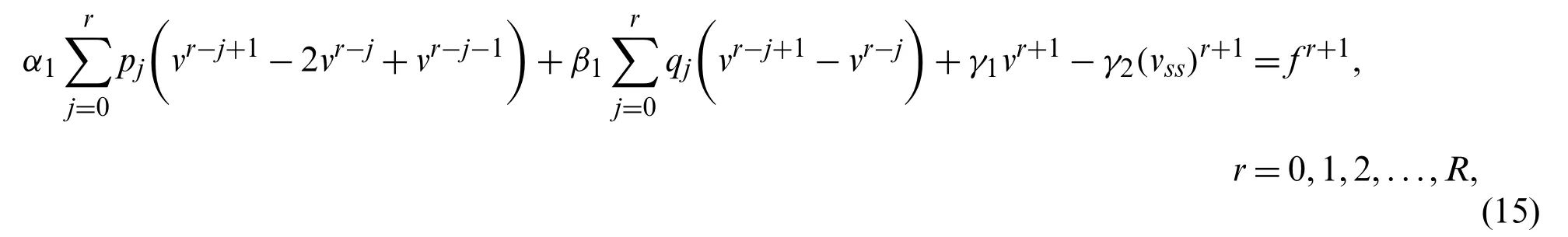
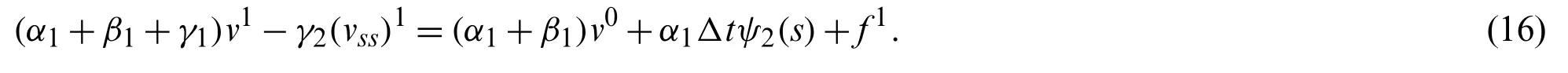
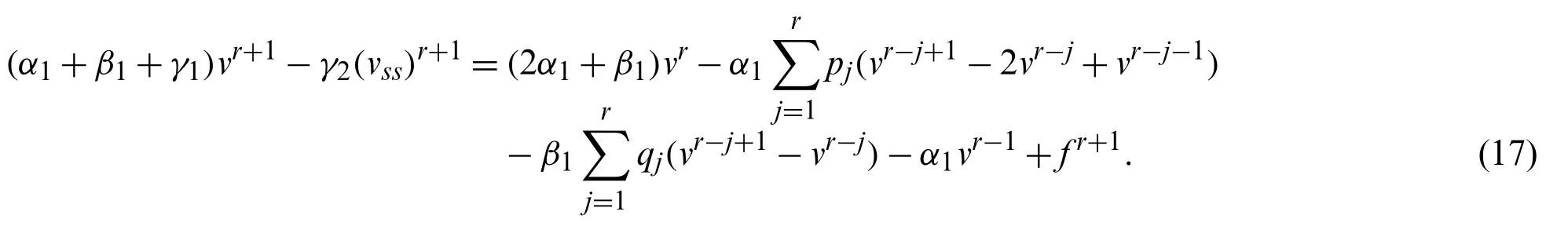


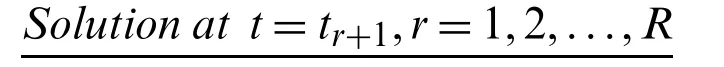

4 Stability


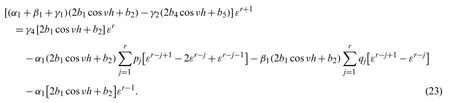

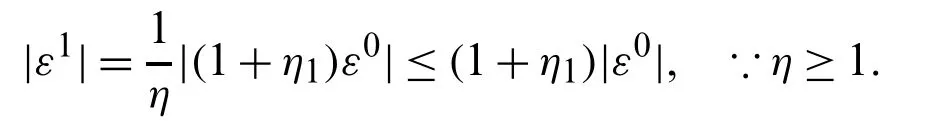

5 Convergence
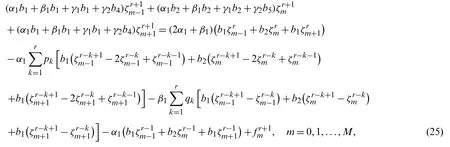


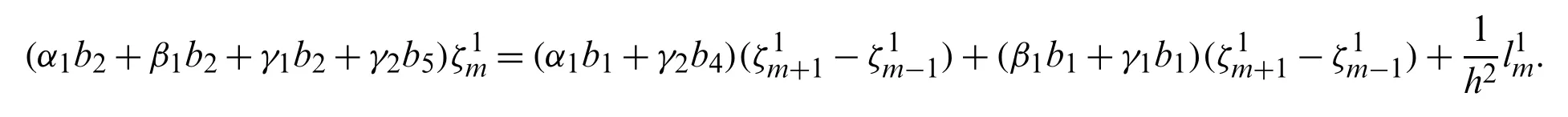
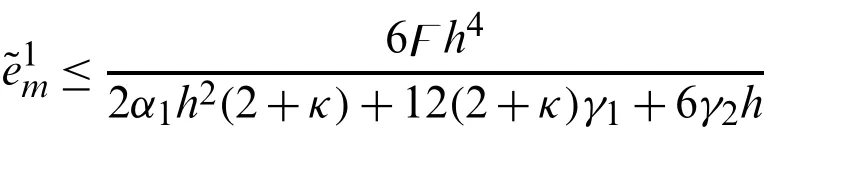

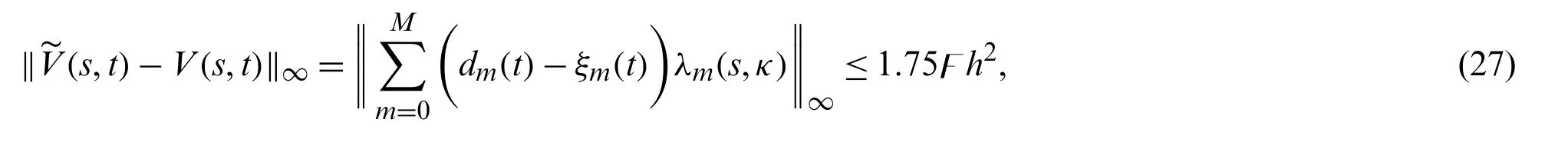
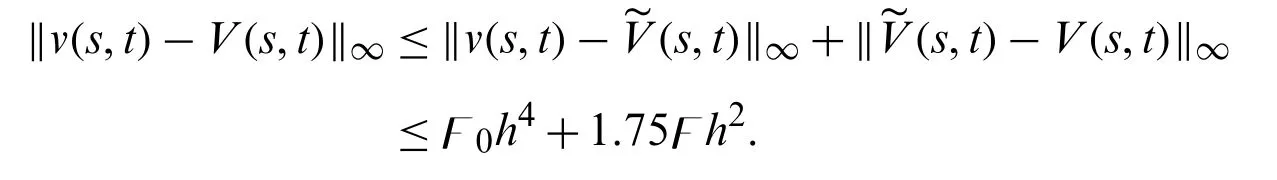
6 Numerical Results

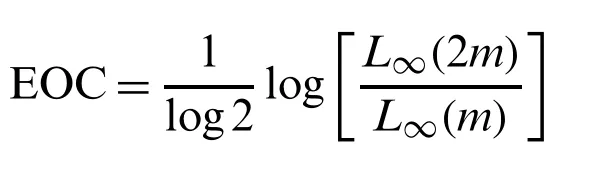
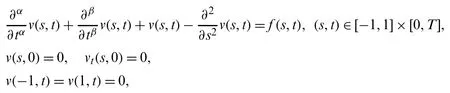
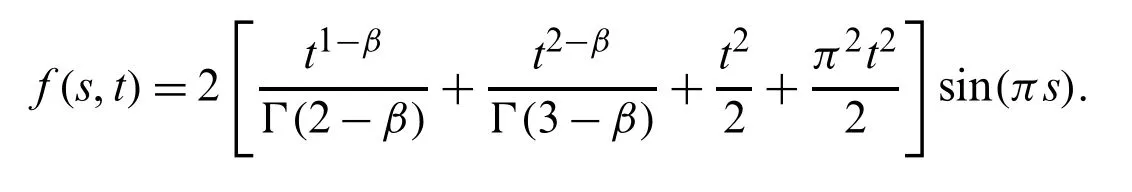

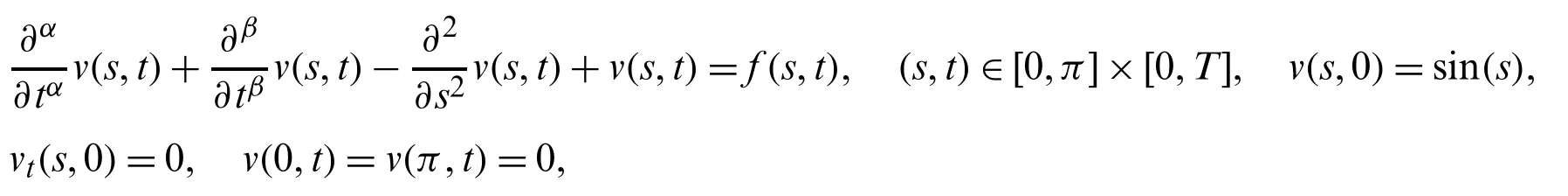






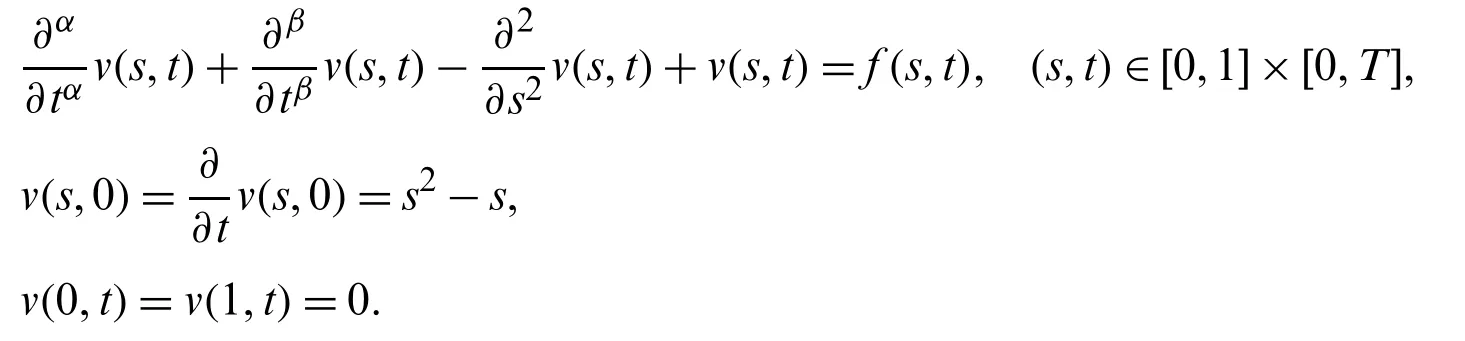
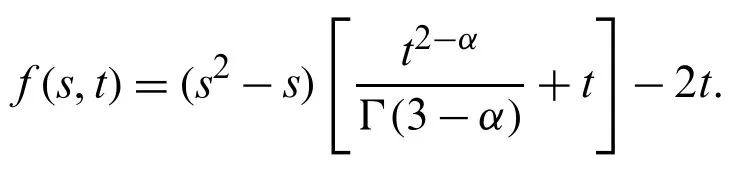





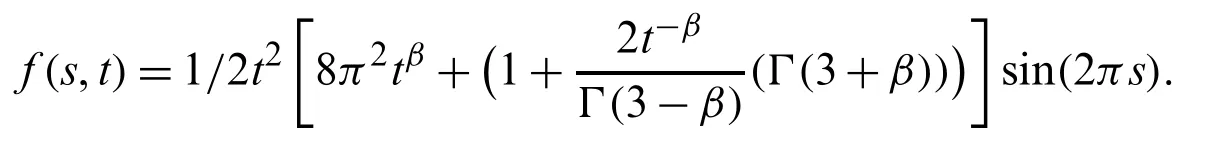



7 Conclusion
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- Nonlinear Problems via a Convergence Accelerated Decomposition Method of Adomian
- Exact Run Length Evaluation on a Two-Sided Modified Exponentially Weighted Moving Average Chart for Monitoring Process Mean
- An Effective Feature Modeling Approach for 3D Structural Topology Design Optimization
- Three-Dimensional Modeling of the Retinal Vascular Tree via Fractal Interpolation
- Experimental and Numerical Study on the Shear Strength and Strain Energy of Rock Under Constant Shear Stress and Unloading Normal Stress
- Eliciting Requirements from Stakeholders’Responses Using Natural Language Processing
