Exact Run Length Evaluation on a Two-Sided Modified Exponentially Weighted Moving Average Chart for Monitoring Process Mean

Piyatida Phanthuna,Yupaporn Areepongand Saowanit Sukparungsee

Department of Applied Statistics,King Mongkut’s University of Technology North Bangkok,Bangkok,10800,Thailand

ABSTRACT A modified exponentially weighted moving average (EWMA) scheme is one of the quality control charts such that this control chart can quickly detect a small shift .The average run length (ARL)is frequently used for the performance evaluation on control charts.This paper proposes the explicit formula for evaluating the average run length on a two-sided modified exponentially weighted moving average chart under the observations of a first-order autoregressive process,referred to as AR(1)process,with an exponential white noise.The performance comparison of the explicit formula and the numerical integral technique is carried out using the absolute relative change for checking the correct formula and the CPU time for testing speed of calculation.The results show that the ARL of the explicit formula and the numerical integral equation method are hardly different,but this explicit formula is much faster for calculating the ARL and offered accurate values.Furthermore,the cumulative sum,the classical EWMA and the modified EWMA control charts are compared and the results show that the latter is better for small and intermediate shift sizes.In addition,the explicit formula is successfully applied to real-world data in the health field as COVID-19 data in Thailand and Singapore.

KEYWORDS Explicit formula;average run length;modified EWMA chart;AR(1) process;exponential white noise

1 Introduction

Statistical analysis is important for confirming consistency and has received interest from many business areas requiring increased reliability.In the manufacturing industry,statistical process control is used extensively and a control chart is one of the quality control tools and has been applied in many fields such as finance [1],health [2] and medicine [3].In 1924,Shewhart created the first control chart which can detect a large-sized process shift quickly [4].Next,the exponentially weighted moving average (EWMA) chart [5] and the cumulative sum (CUSUM)chart [6] were developed and found to be faster for small shift detection.In addition,other new control charts have been developed,one of which is the modified EWMA control chart.Patel et al.[7] expanded the modified EWMA control chart from a fusion of the characteristics of the Shewhart and EWMA control charts that could detect a small size shift quickly and was more effective for autocorrelated data.The modified EWMA statistic is based on the classical EWMA statistic by using past observations with additional consideration of changes in the recent past for pairs of observations in the process.Next,Khan et al.[8] increased the performance of the modified EWMA scheme by maintaining a constantrin the last term of the modified EWMA statistic.

The average run length (ARL) [9] is the average number of in-control observations before an out-of-control signal occurs and is classified based on two stages:ARL at the initial mean(ARL0) and ARL when the process mean has shifted (ARL1).It is now a popular performance measure for a control chart and has been frequently used for research evaluation with many methods,such as Monte Carlo simulation,a Markov Chain approach,a Martingale approach,a numerical integral equation (NIE),and an explicit formula.All of these methods can be used to approximate the ARL but only the last one can be calculated using the least time and obtained the accuracy ARL.For research examples,Flury et al.[10] simulated the ARL to evaluate the multivariate EWMA control chart performance with highly asymmetric gamma distributions.The Markov Chain approach was used by Chananet et al.[11] for the ARL evaluation of EWMA and CUSUM control charts based on the zero-inflated negative binomial (ZINB) model.The Martingale approach was predicated by Sukparungsee [12] to approximate the ARL with optimal parameters of one and two-sided EWMA control chart.

There are many examples in the literature of using the explicit formula and the NIE method for the ARL on control charts.First,Suriyakat et al.[13] presented an explicit formula and a numerical method to solve the ARL on an EWMA control chart for a first-order autoregressive(AR(1)) process with an exponential white noise.Meanwhile,Busaba et al.[14] proposed numerical approximations of ARL on a CUSUM chart for an AR(1) model with exponential white noise.Next,Pecharat et al.[15] derived an explicit formula and a numerical integration scheme for the ARL on a CUSUM control chart for a moving average process of order q (MA(q)) with an exponential white noise.Later,Peerajit et al.[16] solved the NIEs for the ARL for a long memory process with non-seasonal and seasonal autoregressive fractionally integrated moving average (ARFIMA) models on a CUSUM control chart.After that,Sukparungsee et al.[17]analyzed explicit formulas of the ARL for an EWMA control chart using an autoregressive model.Moreover,Sunthornwat et al.[18] reported an explicit formula and a numerical technique to find the ARL on an EWMA control chart for a long memory ARFIMA process,and also presented the evaluation of ARL of an EWMA control chart for a long memory ARFIMA process with optimal parameters [19].Recently,Peerajit et al.[20] introduced the ARL evaluation for CUSUM chart on a seasonal autoregressive fractionally integrated moving average (SARFIMA) process with an exponential white noise by using explicit analytical solutions.

Autoregressive models are often used on control charts in the recent literature [21–23].The order of an autoregressive model is the number of immediate previous values used to predict the present value.A first-order autoregressive model considered in this research is an appropriate process for numerous data sources in real life such as environmental [24],physical [25] and industrial [26] data.Moreover,the modified EWMA control chart can be effectively used with an autocorrelated data.

In this paper,we present the explicit formula to evaluate the ARL on a two-sided modified EWMA control chart for the AR(1) process with an exponential white noise,which is the error term with an exponential distribution that has been studied recently [27–29].In the next section,the AR(1) process features are shown and applied to a modified EWMA scheme.Following this,the ARL is calculated using the explicit formula and the NIE method,and after that,the performance of the schemes to detect shifts between the CUSUM,the classical EWMA and the modified EWMA control charts with simulated and real-world data are reported and compared.

2 Control Chart and Process

2.1 Classical and Modified EWMA Control Charts

The modified exponentially weighted moving average (EWMA) control chart introduced by Patel et al.[7] and Khan et al.[8] were adjustments of the classical EWMA scheme.Let {Xt}fort=1,2,3,...be a sequence of random variables on the AR(1) process with meanμand varianceσ2,andλis an exponential smoothing parameter,where 0<λ<1.The modified EWMA statistic with adjusted constantris expressed as:

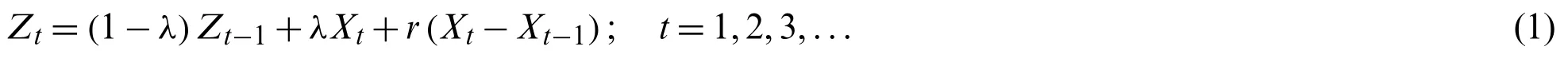
and the asymptotic variance ofZtisFrom Eq.(1),we can show that

(1) Ifr=0,the classical EWMA statistic coincides withZt=(1−λ)Zt−1+λXt.

(2) Ifr=1,the primal modified EWMA statistic coincides withZt=(1−λ)Zt−1+λXt+(Xt−Xt−1).

The upper and lower control limits of the classical EWMA control chart are:

and the bound control limits of the modified EWMA control chart are:

whereμis the process mean,σis the process standard deviation andLandLmare suitable control width limits.

2.2 CUSUM Control Chart

The cumulative sum (CUSUM) chart has been widely used to detect small shifts similar to the EWMA chart on the control process and was initially proposed by Page [6].Let {Xt} fort=1,2,3,...be a sequence of random variables on the AR(1) process with meanμand varianceσ2.The upper CUSUM statistic can be expressed by:

whereqis usually called a reference value or a constant of CUSUM chart,Z0=uis an initial value withu∈[0,b] andbis an upper control limit (UCL).

2.3 Modified EWMA Chart for the AR(1)Process

The equation of observations for the AR(1) process in the case of an exponential white noise is defined as:

whereXt (t=1,2,3,...)is a sequence of random variables,ηis a suitable constant,φis an autoregressive coefficient(|φ|<1),and εtdenotes white noise sequences of the exponential distribution(εt～Exp(β)).

The modified EWMA statistic under the upper bound assumption for the AR(1) process substituted from Eq.(5) into Eq.(1) can be arranged by recursion:

whereZ0=uis the initial value.Therefore,

Zt=(1−λ)u+(λφ+rφ−r)Xt−1+(r+λ)εt+(r+λ)η.

The corresponding stopping time for detecting an out-of-control process on a two-sided modified EWMA control chart can be written as:

whereais the lower control limit andbis the upper control limit.IfZtis in an in-control process and substituted with the term of εt,then

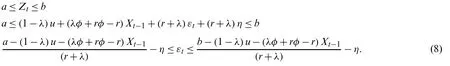
The ARL of the modified EWMA control chart with the AR(1) model is given by:

whereθis the change-point time,Eθ(·)is the expectation under the assumption that the changepoint occurs at timeθ.

3 Integral Equation Method for Solving ARL

For analytical solutions,the ARL on the modified EWMA control chart with the AR(1)model is developed under the condition of a unique integral equation.L(u)is defnied for an initial ARL andIn accordance with the method of Champ et al.[30],L(u)can be found as:

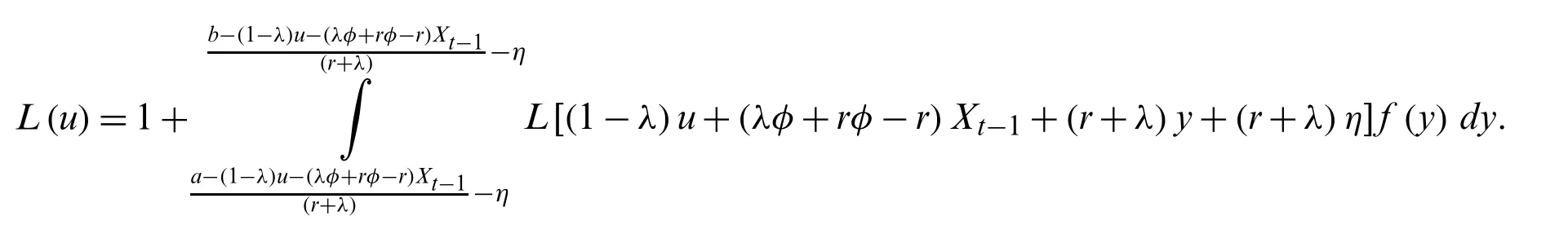
Ifk=(1−λ)u+(λφ+rφ−r)Xt−1+(r+λ)y+(r+λ)ηis defined for changing the variable of integration,thenL(u)is transformed as:

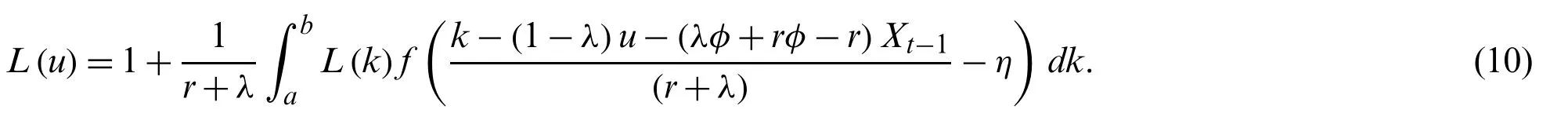
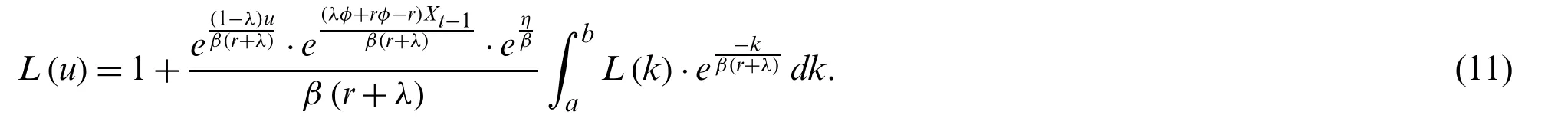
From Eq.(11),the existence and uniqueness of the solutions for the integral equation are proved by the mathematical theory.The integral equation for solving the ARL on the modified EWMA chart with the AR(1) process is proved that can be existed and has a unique solution by using Banach’s fixed point theory [31].

Theorem 1:LetXbe a complete metric space(V,‖·‖).Ifis a contraction mapping whereby:X→X,thenhas a unique fixed pointx.

Theorem 2:LetXbe a complete metric space(V,‖·‖).:X→Xis a contraction mapping ifLis any vector inXandhas a Lipschitz constantc∈[0,1)such thatand

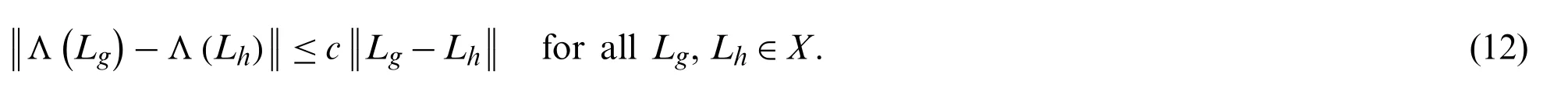
Proof:For a first part,letbe a contraction mapping in the complete metric space(V,‖·‖)whenL0∈V,and define a sequence {Ln}n∈Ngiven byLn+1=forn≥0.Show thatsuch that {Ln}n∈Nis supposed to be Cauchy sequence,so

‖Ln+1−Ln‖=‖−−1)‖≤c‖Ln−Ln−1‖≤cn‖L1−L0‖

where ‖L1−L0‖ is a finite number.After that,using this solution and the triangle inequality for allm>n≥Ncan be solved as:

whereε>0 andc∈[0,1).Therefore,the sequence {Ln}n∈Nis a Cauchy such that:

Thus,Lis called a fixed point of.

Next part has to show that this fixed point is unique.GivenLg,Lh∈Vin the complete metric space(V,‖·‖)for allu∈[a,b],then Eqs.(11) and (12) are considered as:

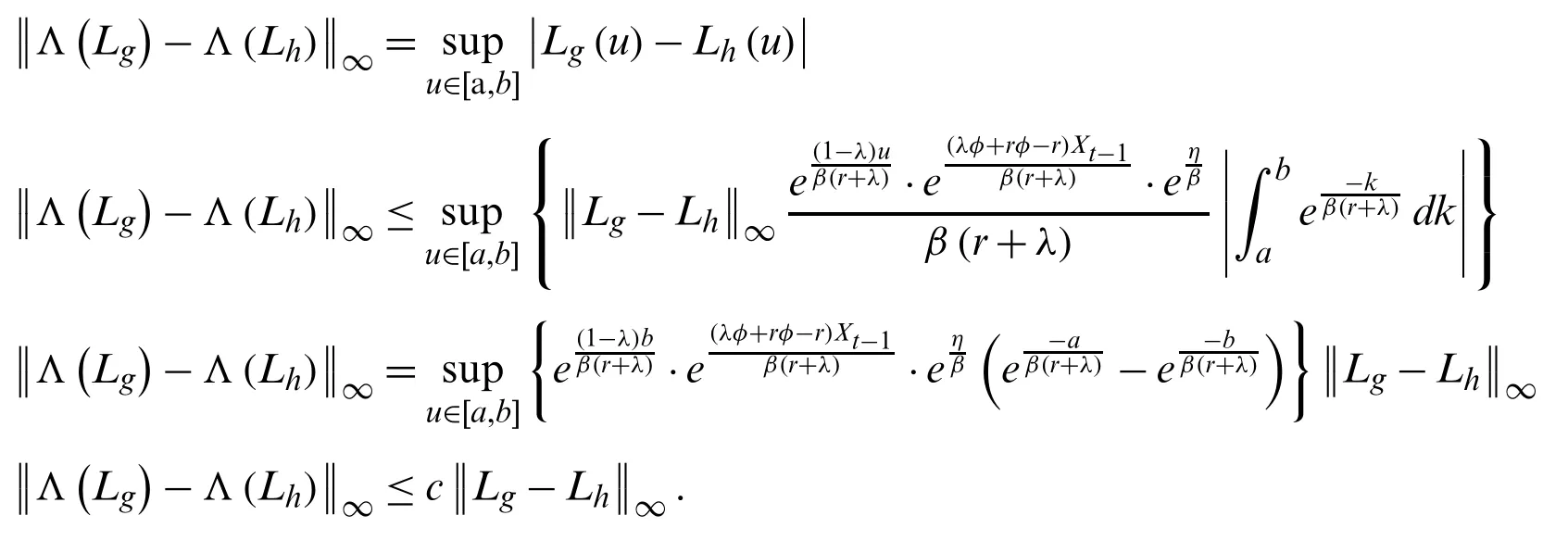
4 Explicit Formula for ARL

The explicit analytical solutions of the ARL on the modified EWMA control chart with the AR(1) model constructed after checking for unique solutions are:

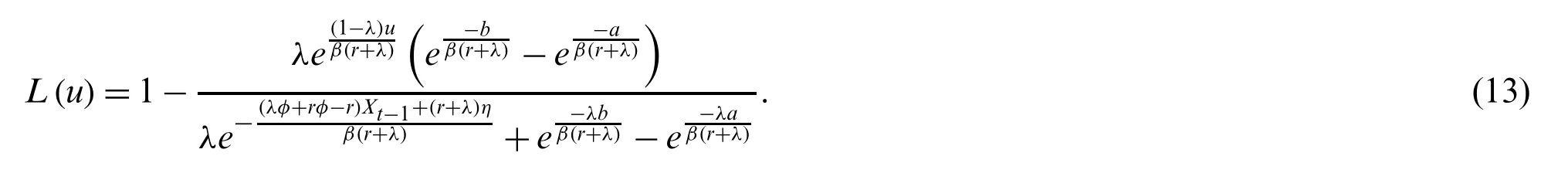
Proof:In the first step,the solution of Eq.(11) as:is determined as:which is a constant andsuch that it can be rewritten as:

ConsiderDand take turnsL(k)with Eq.(14),then

Finally,by substituting constantDfrom Eq.(15) into Eq.(14),thenL(u)can be found:

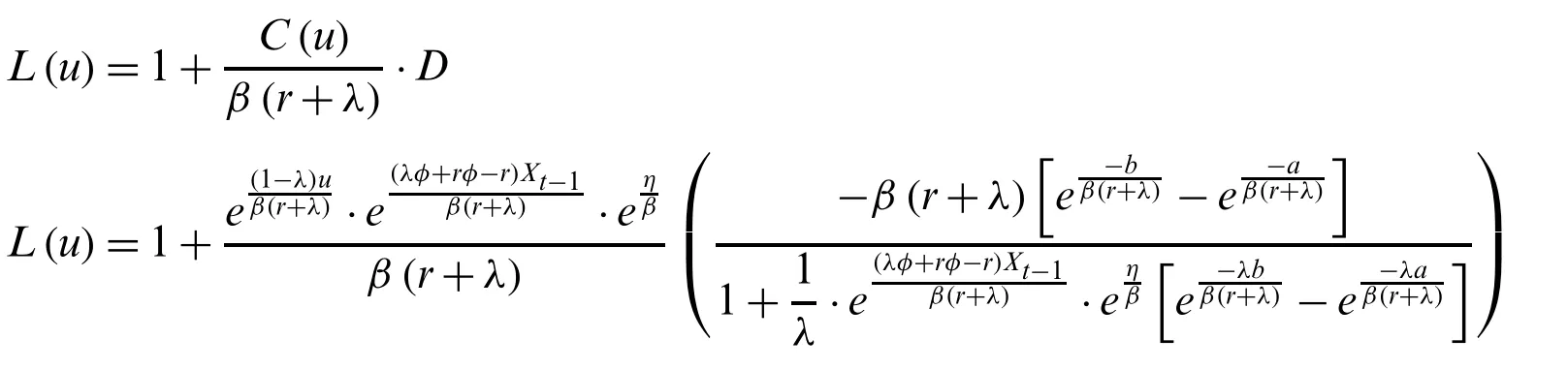
Therefore,the solution to Eq.(13) is obtained.

For an in-control process,the exponential parameter is set toβ=β0and the explicit formula withβ0called ARL0can be written as:

On the other hand,the exponential parameter for an out-of-control process is defined asβ1=(1+δ)β0,whereβ1>β0andδis the shift size such that the explicit formula ofβ1can be described as:

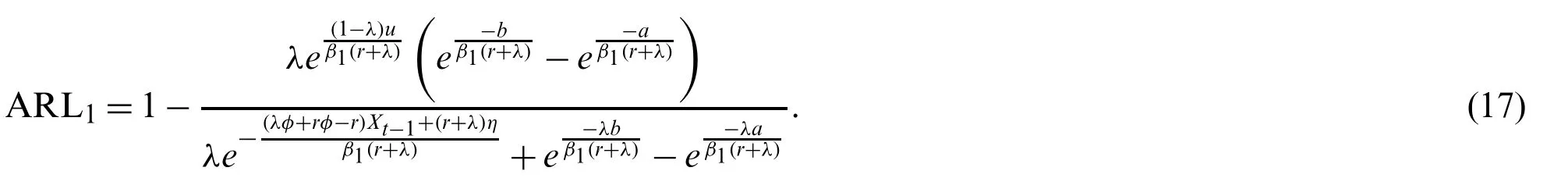
5 Numerical Method for Solving the Integral Equation

The NIE method is used to solve the ARL for the AR(1) process of the two-sided modified EWMA control chart in Eq.(10).The ARL solution orLNIE(u)is approximated with themlinear equation systems over the interval [a,b] by using the composite midpoint quadrature rule [32].This NIE method is proposed for the two-sided modified EWMA control chart by using the length ofmequal divided intervalsand the middle point of thejthintervalTherefore,the ARL solution of the NIE method can be rewritten as:

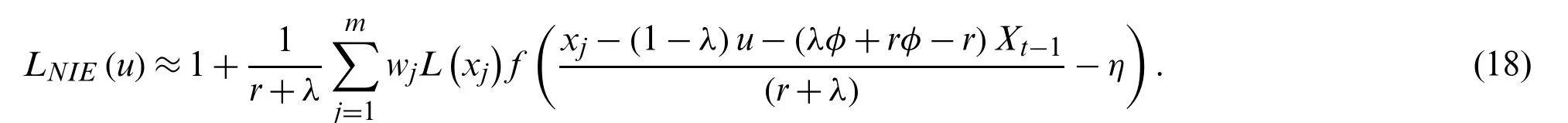
6 Comparison of the ARL Results

In this section,the performances of the explicit formula and the NIE method are compared by using the ARL solutions such that the NIE method determines the number of division pointsm=1,000.ARL0of 370 is used for the experiments with the classical and modified EWMA control charts and the AR(1) process;a lower ARL value signifies better effective detection.For the in-control process,the initial parameter valuesβ0=1,u=1,X0=1 as this process mean are determined.In addition,the process mean is tested with shift sizes(δ)of 0.01,0.02,0.03,0.04,0.05,0.06,0.08,0.10,0.20,0.30,0.40,0.50,0.60,0.80 and 1.00.The optimization procedure in Fig.1 can be summarized as follows:

Step 1:Specifyλ,φ,η,rand ARL0.

Step 2:Determine the initial values of the process mean on an exponential distribution as:β0,u,X0.

Step 3:Computebwhenais known by using Eq.(13) for the explicit formula or Eq.(18)for the NIE method.

Figure 1:The summarized processing diagram

Step 4:Compute ARL1from thebsolution in Step 3 by shifting mean(δ)whereβ1=(1+δ)β0.

The efficiency comparison of the ARL between the explicit formula and the NIE method is measured using the absolute relative change (ARC) [33] which can be calculated as:

Table 1:Comparison of ARL values on the modified EWMA control chart with the AR(1) model using explicit formulas against the NIE method given λ=0.05,η=2,r=1,a=0 at φ=0.1(b=0.333987011),φ=−0.1 (b=0.408730497) for ARL0=370

In addition,the speed test results are computed by the CPU time (PC System:Windows 10 Education,i7-6500U CPU@2.50 GHz Processor,8.00 GB RAM,64-bit Operating System)in seconds.

Table 2:Comparison of the ARL values between the CUSUM,the classical EWMA and modified EWMA control charts given λ=0.05,η=2,a=0 at ARL0=370

The performance comparison of the explicit formula and the NIE method is explained with the ARL,the ARC and the CPU time (Tab.1).The first results indicate that the ARL values of the explicit formula are similar to those of the NIE method according to the ARC criterion such that ARC solutions are very low and converge to 0.For the CPU time for calculating the ARL,the explicit formula is faster than the NIE method by around 9 s.

The performance of the modified EWMA control chart on varying scales of constantr,different bound control limits [a,b] and variousλare further tested by using the relative mean index (RMI) [34] which can be written as:

whereARLi(c)is the ARL of the control chart for the shift size of rowi,ARLi(s)is the smallest ARL of all of the control charts on rowiand the RMI value is smaller,then the control chart has more performance for detecting shifts.

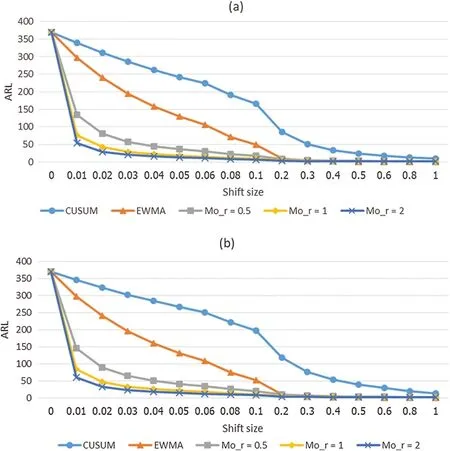
Figure 2:Plot of the CUSUM,the classical EWMA and modified EWMA control charts given(a) φ=0.2 and (b) φ=−0.2

The CUSUM,the classical EWMA (r=0),the classical modified EWMA (r=1) and the modified EWMA control charts with adjustedr=0.5 andr=2 measured a capability by using the ARL and the RMI atφ=0.2,−0.2 for ARL0=370 are compared and reported in Tab.2 and Fig.2.When the process mean is shifted,the ARL results of the modified EWMA control charts have abrupt decrease and lower values in small and intermediate shifts.For large shifts,the classical EWMA chart is obtained the least ARL.Therefore,the performance of modified EWMA control charts is better than the classical EWMA scheme for small and intermediate shifts.Moreover,the results show that the CUSUM chart has lower performance than modified EWMA control charts for all levels of shifts.From ARL and RMI comparisons,the modified EWMA control charts with higherrvalues are more effective.

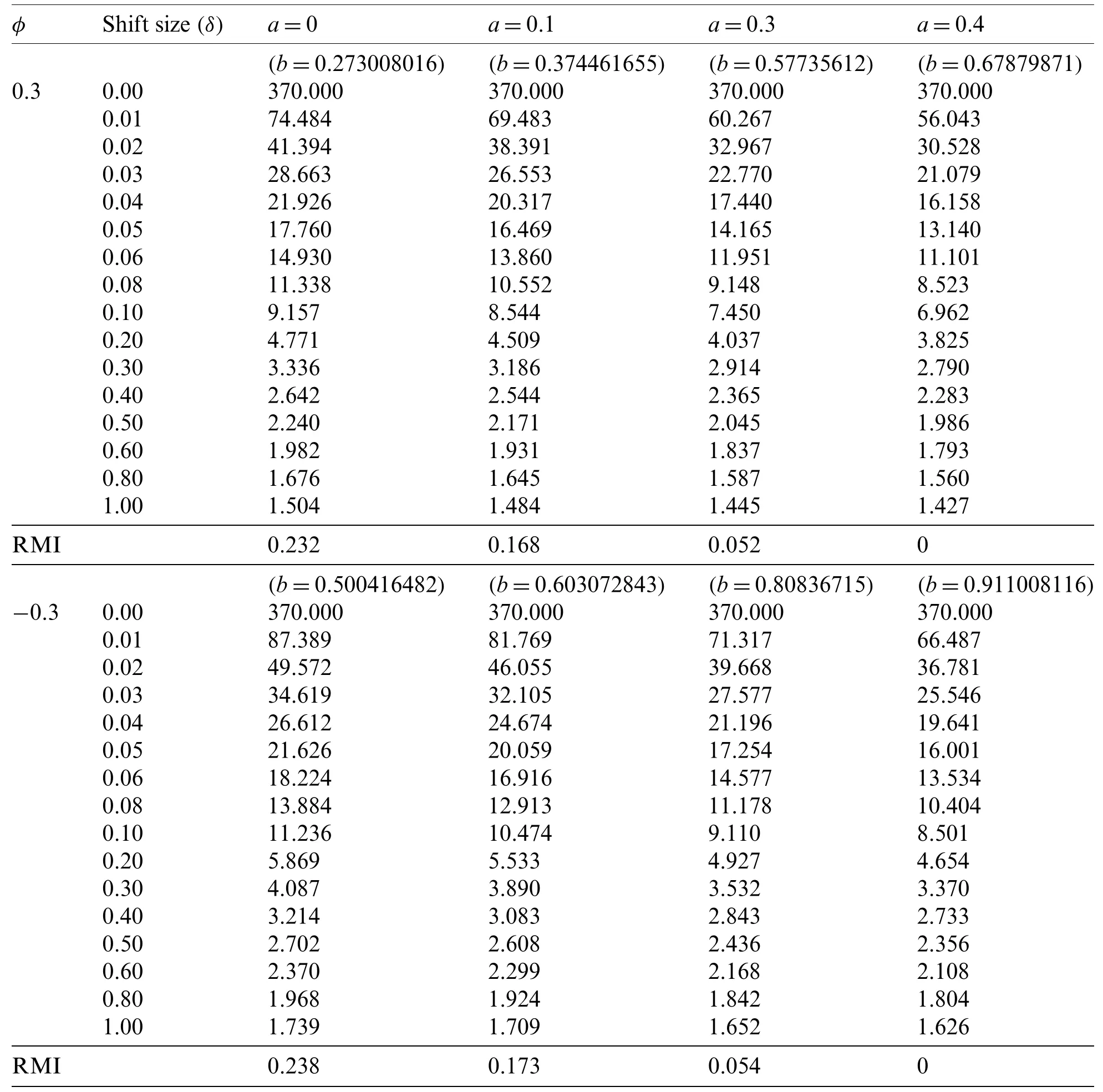
Table 3:Comparison of the ARL values on the modified EWMA control chart with difference control bounds given λ=0.05,η=2,r=1 at ARL0=370

For Tab.3,the ARL results with ARL0=370 show the performance of the modified EWMA control chart on various bound control limits [a,b] forφ=0.3,−0.3 anda=0,0.1,0.3,0.4.The RMI values of the lower bounda=0.4 are 0.When the lower bound (a) is higher,then the modified EWMA control chart can detect better shifts when comparing the ARL and the RMI values in one direction.

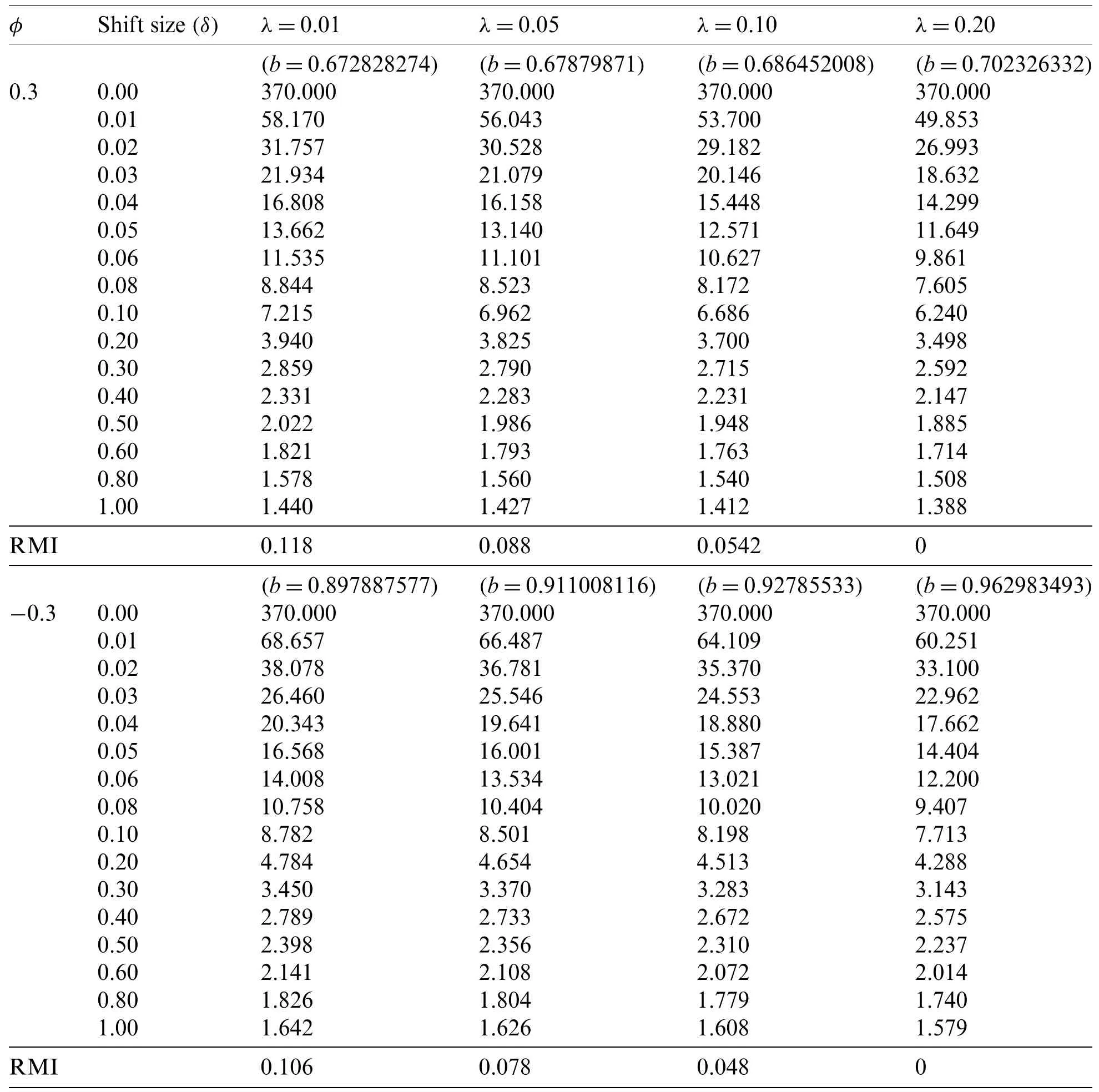
Table 4:Comparison of the ARL values on the modified EWMA control chart with various λ given η=2,r=1,a=0.4 at ARL0=370

Moreover,the modified EWMA control chart is compared for variousλ=0.01,0.05,0.10 and 0.20 at ARL0=370,a=0.4 andφ=0.3,−0.3 (Tab.4).The RMI values ofλ=0.20 are 0.The ARL and the RMI results show that moreλvalues affect for increasing a detected performance of the modified EWMA control chart.

Figure 3:Plot of the noise residual of COVID-19 data in Thailand

Figure 4:Plot of the noise residual of COVID-19 data in Singapore

7 Application to Real Data

As an example,the modified EWMA control chart is applied to COVID-19 data in Thailand and Singapore [35,36] such that the 100 days of newly infected cases are studied when the more summation of 100 cases.These data are checked to a suitable AR(1) process with an exponential white noise at parameters of COVID-19 data in Thailandβ0=34.78,η=10.06,φ=0.664 and Singaporeβ0=159.47,η=48.99,φ=0.863.Moreover,their error term have be tested an exponential distribution and plotted graphs in Figs.3 and 4,respectively.

Table 5:Comparison of ARL values between the CUSUM,the classical EWMA and modified EWMA control charts for COVID-19 data in Thailand with β0=34.78,η=10.06,φ=0.664,a=0 at λ=0.05 and ARL0=370

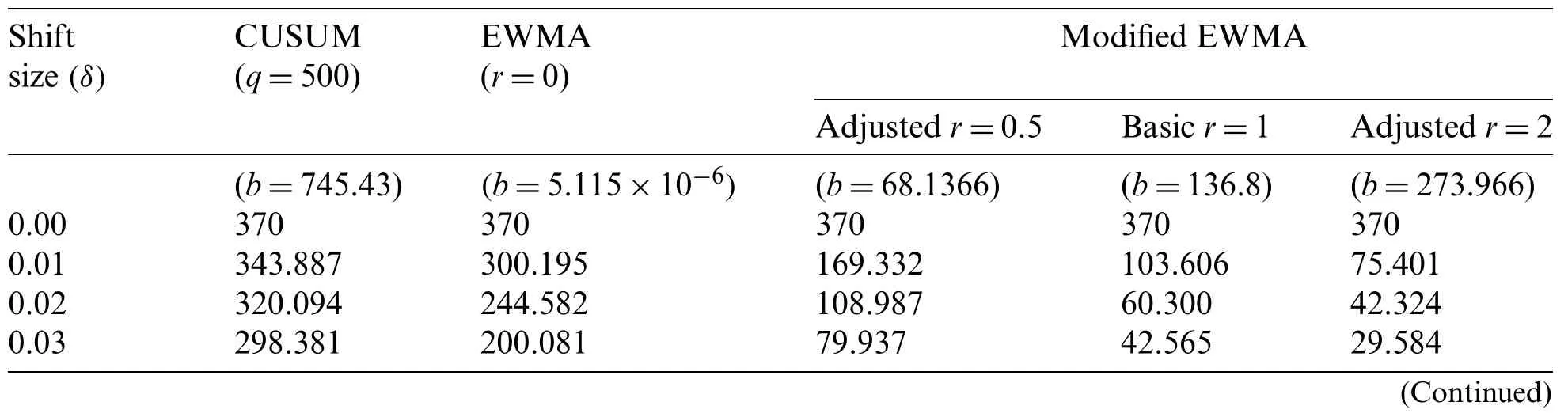
Table 6:Comparison of ARL values between the CUSUM,the classical EWMA and modified EWMA control charts for COVID-19 data in Singapore with β0=159.47,η=48.99,φ=0.863,a=0 at λ=0.05 and ARL0=370

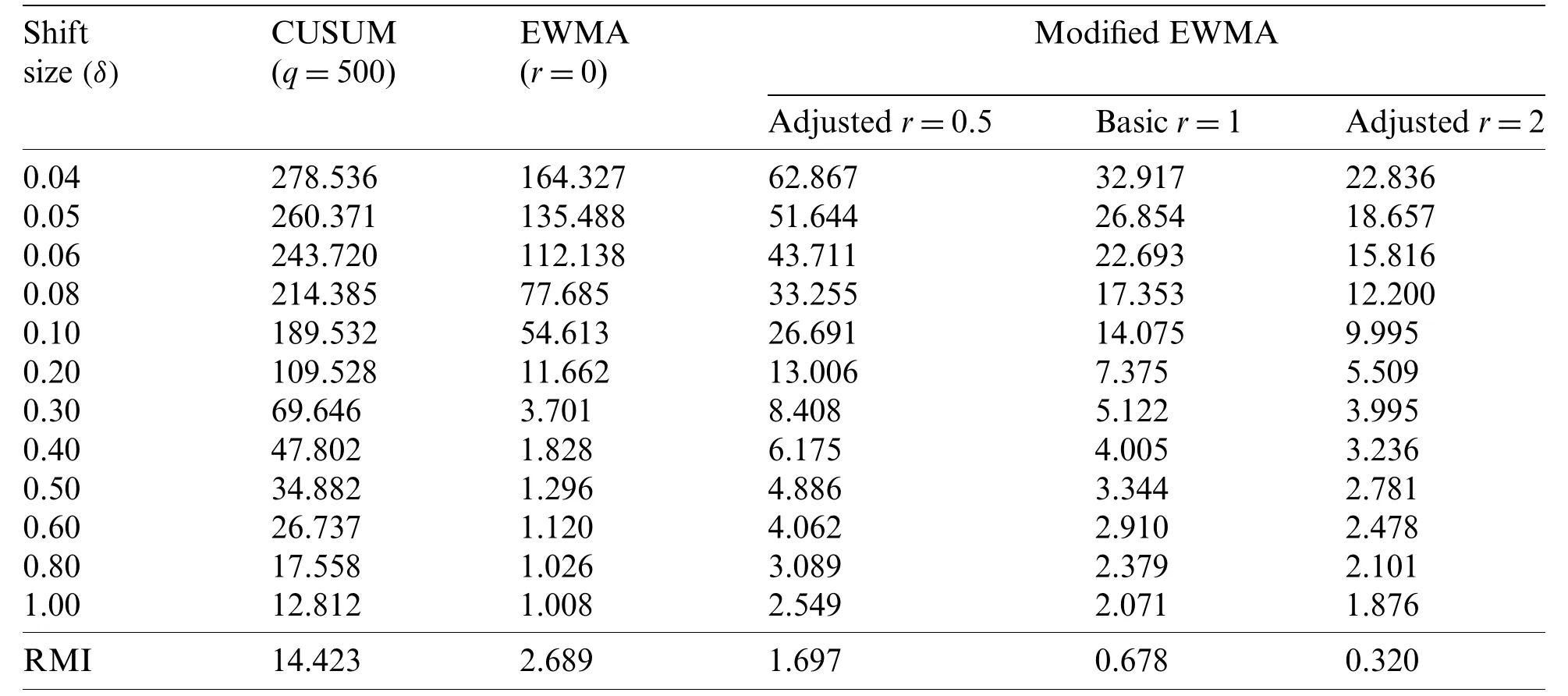
Table 6:Continued

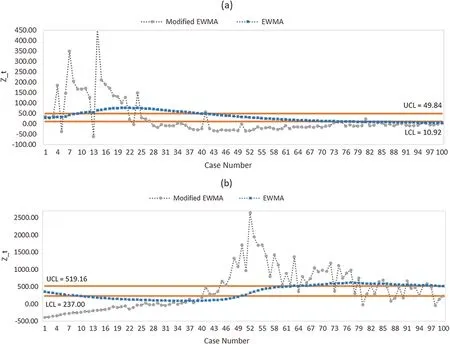
Figure 5:Plot of the classical EWMA and modified EWMA control chart with r=2 for COVID-19 data in (a) Thailand and (b) Singapore

From Tabs.5 and 6,the results of ARL and the RMI are used to compare the CUSUM,the classical EWMA and modified EWMA control charts with real-world data of COVID-19 data in Thailand and Singapore.The results are in accordance with the simulation data in Tab.2 and show that the modified EWMA control chart adjusted for highrperforms well for small and intermediate level shifts.

In Fig.5,the modified EWMA control chart withr=2 and the classical EWMA control chart are plotted by calculatingZtof COVID-19 data in Thailand and Singapore at the exponential smoothing parameterλ=0.05 with the optimal control width limit of EWMA chartL=2.615 [37] and the calculated control width limit of the modified EWMA chartLm=0.204 at bound control limits of Thailand [10.92,49.84] and bound control limits of Singapore[519.16,237].The results show thatZtvalues of the modified EWMA control chart withr=2 exceed the bound since the 4thobservation,whileZtvalues of the classical EWMA control chart are the out-of-control limit at the 9thobservation for Thailand.In Singapore,Ztvalues of the modified EWMA control chart withr=2 exceed the bound since the first observation,while the classical EWMA control chart signals an alarm in the 10thobservation.Therefore,the modified EWMA control chart can detect shifts more quickly than the classical EWMA control chart.

8 Discussion and Conclusions

The performance of a control chart can be evaluated by using the ARL.In this paper,the explicit formula and the numerical integral equation (NIE) method of ARL solutions are established on a two-sided modified EWMA control chart for an AR(1) process with an exponential white noise.The ARL results of both methods are computed and their performances compared via the ARC and the CPU time.The explicit formula shows the actual values of the ARL and is faster calculation than the NIE approach.Moreover,the ARL and RMI results are compared between the CUSUM,the classical and modified EWMA control charts with variousr,for which the latter provides better detection for small and intermediate shifts.Next,the performance of the modified EWMA control chart is tested on various bound control limits and is found to be better for higher upper bound values.In addition,this model is applied to the real-world data (COVID-19 data in Thailand and Singapore),with which it obtains similar results as with the simulated data;this result supports the excellent performance of the modified EWMA control chart.In future research,we will establish the optimal bound control limits of the modified EWMA control chart and hope to extend our approach to many new control charts currently under development for different processes.

Funding Statement:The research was supported by King Mongkut’s University of Technology North Bangkok Contract No.KMUTNB-62-KNOW-018.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.