Behavior of High Strength Concrete Filled Square Steel Tube Stub Columns with Inner CFRP Tube Under Biaxial Eccentric Compression
2021-04-27ZhijianYangGuochangLiYanLangandZengmeiQiu
Zhijian Yang,Guochang Li,*,Yan Lang and Zengmei Qiu
1School of Civil Engineering,Shenyang Jianzhu University,Shenyang,110168,China
2Department of Building Engineering,Suqian College,Suqian,223800,China
ABSTRACT This paper studies the contribution of CFRP (carbon fiber-reinforced polymer) to the mechanical behavior of high strength concrete-filled square steel tube (HCFST) under biaxial eccentric compression.The new type of composite member is composed of an inner CFRP tube and an outer steel tube with concrete filled in the two tubes.The finite element analysis was made by ABAQUS on the behavior of high strength concrete filled square steel tubular columns with inner CFRP circular tube subjected to bi-axial eccentric loading.The results obtained from the finite element analysis were verified with the experimental results.In addition,the load-deflection curves in the whole process were calculated and analyzed,which can be divided into three segments:Elastic phase,plastic phase,descending phase.Based on the load-deflection curves,the stresses analysis on the core concrete,CFRP tube and steel tube were conducted.The confinement effect of the CFRP tube improves the ductility of HCFST-CFRP stub column.CFRP ratio and eccentricity affect the ultimate bearing capacity of HCFST stub column.Finally,a calculation formula of ultimate bearing capacity was proposed in the paper.
KEYWORDS CFRP tube;concrete-filled square steel tube;high strength concrete;bi-axial bending;stub column
1 Introduction
Concrete filled steel tube columns have been widely used in high rise building,bridge and other projects because of their high bearing capacity,good seismic performance,fire resistance and so on.Compared with concrete-filled circular steel tube column,the connection between column and beam of concrete filled square steel tube (CFST) column is more simple and convenient,therefore,the CFST columns have been widely applied in building [1].
The confinement effect of square steel tube to concrete is inferior to circular steel tube,which causes the CFST column could not perform as well as concrete filled circular steel tube column.Therefore,the circular CFRP tube was embedded into the CFST column to improve the confinement effect of square tube.Some results have shown that the CFRP tube,steel tube and concrete can work well together in CFST column with inner CFRP tube.Li et al.[2–4] conducted test on the behavior of CFST-CFRP specimens subjected to axial load and pure bending.The results showed that the confinement effect of the CFRP tube increased ductility of CFST stub columns remarkably.The inner CFRP was not only to overcome the disadvantages of the highstrength concrete,but also to improve the bearing capacity and the stability of CFST for slender column.The flexural stiffness and the ultimate load of CFST can be substantially improved by the inner CFRP tube.Feng et al.[5,6] studied the CFST with GFRP-confined concrete core;18 stub columns were tested with different concrete strengths,GFRP tube thickness and steel tube thickness in comparison to four traditional composite columns.Test results showed that the strengths of concrete,FRP,and steel could be effectively utilized at different stages.Feng et al.[7]investigated the seismic performance of CFST with GFRP confined concrete core column;the test result showed the specimens exhibited favorable energy dissipation and ductility,even when the columns were subjected to high axial loads.
In actual engineering,the column of structure bears not only vertical load but also wind and earthquake load.Especially for the corner columns in buildings,they may be subjected to bi-axial eccentric compression.Previous researchers have done many works on CFST under eccentric load,but the achievements about CFST columns under biaxial load are few.Mursi et al.[8,9] revealed the beneficial effect of use of filled concrete on delaying the onset of local buckling and global buckling behavior of column,and presented a numerical model to consider the coupled effect of local and global buckling under biaxial conditions.Li et al.[10] reported the test results of high strength concrete filled square steel tube columns considering the slenderness ratio and steel ratio.Guo et al.[11,12] studied concrete filled rectangular steel tube columns subjected to biaxial bending,and the results showed that steel plate appeared local buckling after the specimen reached the ultimate bearing capacity.Liang et al.[13,14] developed a new multiscale model accounted for the effects of local buckling and high strength materials for CFST slender beam-columns under biaxial bending.Li et al.[15,16] carried out an experimental study on the behavior of CFSTCFRP slender column subjected to biaxial eccentric loading,the experimental results showed that the failure mode of HCFST-CFRP was similar to that of HCFST,the steel tube and the CFRP worked together well before failure under bi-axial eccentric loading.Idris et al.[17] conducted test on six square FRP-HSC-steel DSTCs under axial and cyclic lateral load considering the effects of axial load,column aspect ratio,steel tube size and concrete fill.The results showed that the square DSTCs exhibited ductile behavior,filled concrete made a significant increase in the lateral drift capacity.Li et al.[18] proposed a new type of composite column that concretefilled square steel tubular stub column stiffened with an encased I-section CFRP profile,and performed biaxially eccentric compression test on the composite column considering the effects of concrete compressive strength,steel yield strength,and steel ratio.Li et al.[19] conducted eccentric compression tests on high strength concrete fille d high strength square steel tube stub columns,and put forward Formulas to predict the P/Pu-M/Mu curves.
Since the CFST column with inner CFRP tube is a new composite member,limited studies have been conducted on this new composite column under bi-axial eccentric compression and its behaviors have not been understood for engineering applications.This paper experimentally and numerically investigated the behavior of CFST stub column with inner CFRP tube under biaxial eccentric compression.The tests were conducted on fourteen specimens with variations of eccentric ratio,steel ratio,CFRP ratio and concrete strength.The formulas to predict the P/Pu-M/Mucurves were proposed for the stub column under bi-axial eccentric compression.
2 Experiment
Fourteen specimens were designed to study the behavior of high strength concrete-filled square steel tube (HCFST) with inner CFRP tube short column under biaxial eccentric compression.The varied parameters were steel ratio,CFRP ratio,eccentric ratio and concrete strength.The cold-formed square tube was used.The CFRP tube was fabricated by unidirectional carbon fiber sheets.The height of specimen is 600 mm,the width of the square steel tube is 200 mm,and the diameter of CFRP tube is 125 mm.The cross section of HCFST-CFRP column is shown is Fig.1,and the details of the specimens are listed in Tab.1.The material properties of steel and FRP are listed in Tabs.2 and 3.
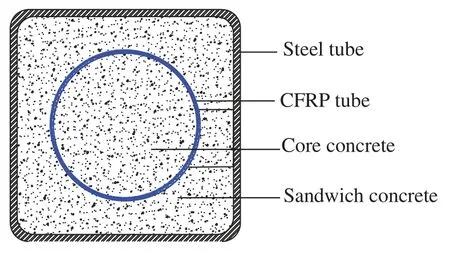
Figure 1:Cross section of HCFSST-CFRP column
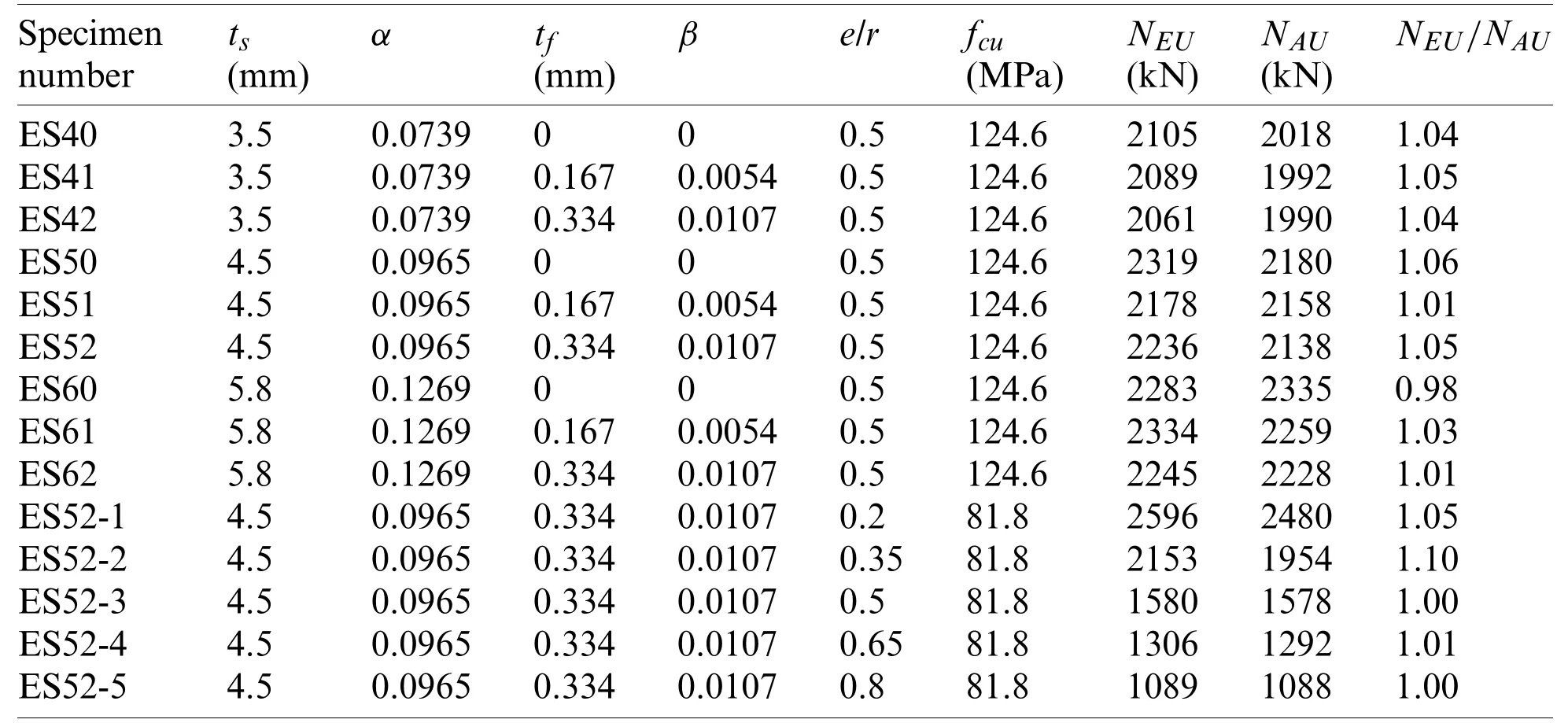
Table 1:Details of the specimens

Table 2:Material property of steel tube

Table 3:Material properties of CFRP
The typical failure mode is shown in Fig.2.It can be seen that the most common exterior failure characteristic of compressive zone is local buckling,crushed sandwich concrete,and broken CFRP,but inner concrete got little crack because of the confinement effect of CFRP tube.The sandwich,inner concrete and adhesive of CFRP appeared cracks in tensile area.

Figure 2:The failure mode of compressive zone of HCFSST-CFRP stub column (a) steel tube(b) sandwich concrete (c) CFRP and inner concrete
3 Finite Element Analysis
The FEA model developed through ABAQUS/Standard was used to simulate high strength concrete filled square steel tube stub columns with inner CFRP tube under biaxial eccentric compression.
3.1 Material Constitutive Model
3.1.1 Steel
The elastic-plastic constitutive model provided by ABAQUS which meets Von Mises yield criterion and Isotropic strengthening rule was adopted to simulate the constitutive relationship of steel.The bilinear constitutive model of steel was used to simulate the steel,shown as follows:

3.1.2 Concrete
The damaged plastic model provided by the ABAQUS library was adopted to simulate the concrete.Considering the concrete was confined by steel tube and CFRP tube,the stress–strain relationship of the concrete proposed by Han was applied for ABAQUS finite element analysis [20].The fracture energy-crack displacement model was used to simulate the tension stress–strain of concrete [21].

wherex=ε/ε0,y=σ/σ0,η=1.6+1.5/x,σ0=f′c(MPa),ξ=fyAs/fckAc,ε0=εc+800ξ0.2×10−6,
In the above equations,fyandfcare the yield strength of steel and the cylinder strength of concrete,respectively;AcandAsare the cross-sectional area of concrete and steel,respectively;fckis the characteristic concrete strength.

whereGfis fracture energy;coefficienta=1.25dmax+10,dmaxis the maximum particle diameter of coarse aggregate.
3.1.3 CFRP
The CFRP tube was assumed to be linear elasticity.The fibers were ruptured when reaching the ultimate strain so the fibers could not take the load,the specific expression as follows:

where,σfis the ultimate stress of the fiber;Efis the modulus of elasticity;εfis the ultimate strain.
3.2 Contact and Boundary Conditions
Fig.3 shows the model of a HCFST-CFRP tube short column under bi-axial eccentric compression.The steel tube and concrete were modeled with 8-node brick elements (C3D8R),and a quad-node first-order reduced integration shell element (S4R) was chosen for CFRP tube.A 1/4 symmetrical model was adopted to improve the model calculation speed,and the contact constraint relationship between materials was simplified.The 1,2,3,and 4 faces were symmetrical along the XZ plane,and the 5,6,7,and 8 faces were symmetrical along the XY plane.
The contact between the core concrete and the CFRP tube,and the contact between the sandwich concrete and CFRP tube were all established with tie to achieve the purpose of displacement coordination and simplifying the model.The contact between the steel tube and the concrete used hard contact,the friction coefficient is 0.6.Considering that numbers of materials were involved in the model and the degree of non-linearity is relatively large,small sliding was adopted to establish the sliding relationship of interface contact.
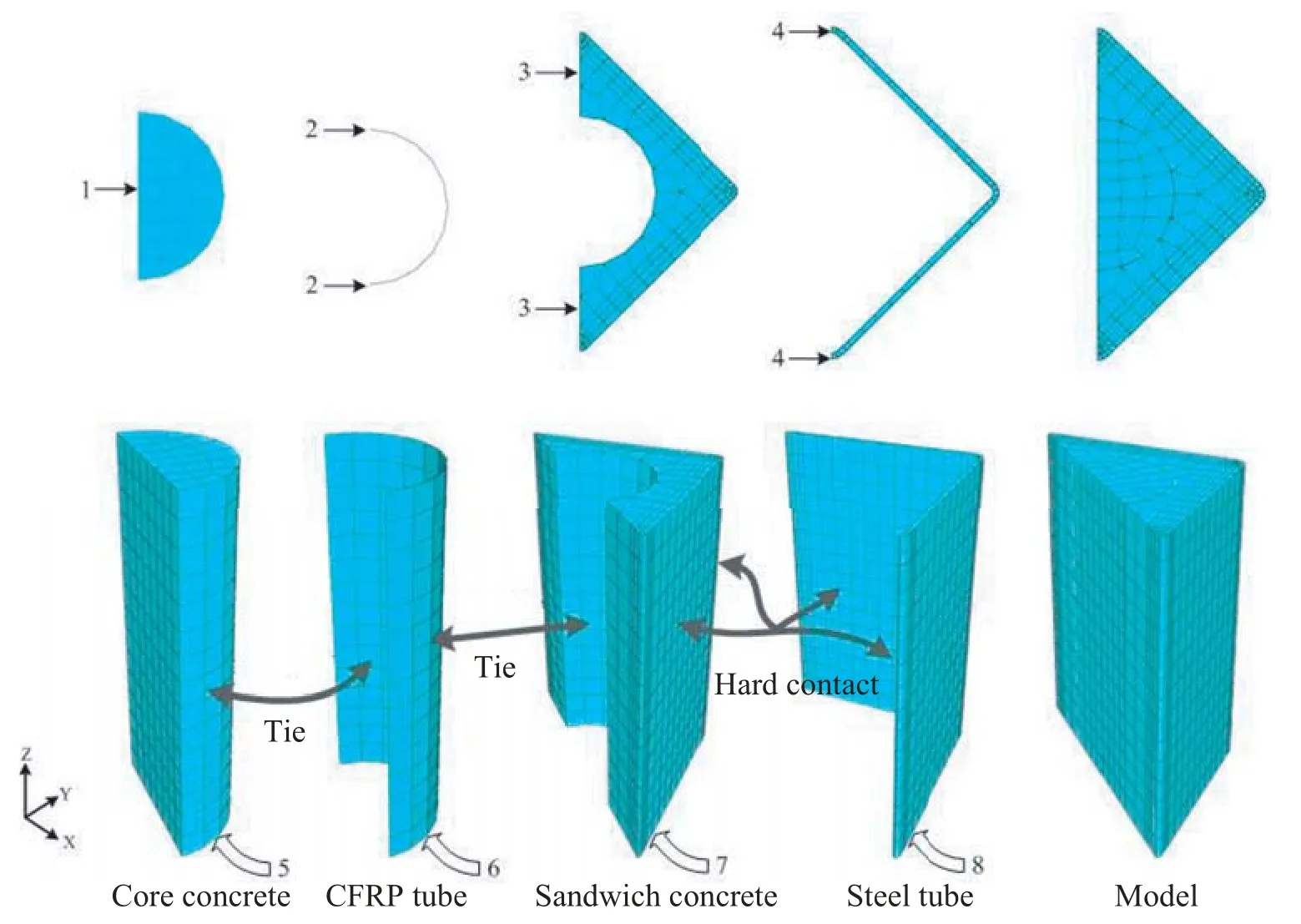
Figure 3:Finite element model
3.3 Results Comparison between FEM and Test
In order to verify the accuracy of the ABAQUS finite element model,the calculation results were compared with the measured results.It can be seen from Fig.4 that the failure mode of the finite element model is consistent with the test.Fig.5 shows the comparison between the finite element analysis calculation curve and the experimental load-deflection relationship curve.It can be seen that the finite element calculation curve is in good agreement with the measured curve.

Figure 4:Failure mode of the specimen

Figure 5:(Continued)
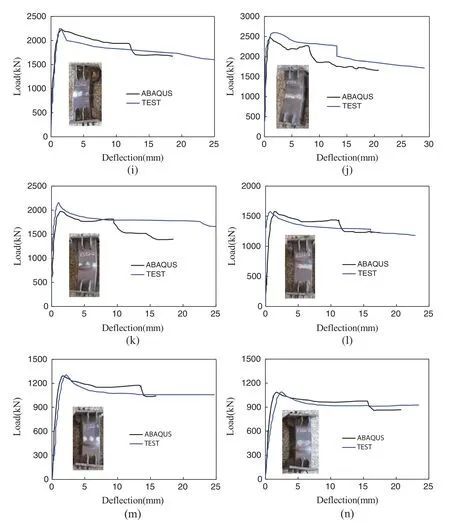
Figure 5:Load-deflection relationship curves (a) ES40,(b) ES41,(c) ES42,(d) ES50,(e) ES51,(f) ES52,(g) ES60,(h) ES61,(i) ES62,(j) ES52-1,(k) ES52-2,(l) ES52-3,(m) ES52-4,(n) ES52-5
After the HCFST-CFRP short column reached its ultimate bearing capacity,the steel tube began to enter the plastic stage.As the load increased,the steel tube in the central compression zone section of specimen appeared local buckling.
3.4 Discussion and Analysis
The loading process of HCFST-CFRP tube short column under biaxial eccentric compression is shown in Fig.6.As shown in Fig.6a,in the initial stage of loading,the lateral deflection of the mid cross section of the specimen was small,and the steel tube and concrete were both in the elastic stage.At this time,the CFRP tube did not play any substantial role.As shown in Fig.6b,as the load increased,steel tube and concrete successively entered the elastoplastic or plastic state.The load was very close to the ultimate bearing capacityNue,and the core concrete of the specimen (including sandwich concrete and concrete filled in CFRP tube) began to appear significant expansion.The sandwich concrete was in a weakly constrained area,causing its volume expansion rate to be relatively fast.At this time,the mid cross section of the steel tube in the compression zone began to appear buckling deformation.Although it was not obvious,the volume expansion (longitudinal micro-crack development) of the sandwich concrete and buckling development of the steel tube were faster.Due to the coordination deformation of the entire specimen,a certain degree of volume expansion also occurred in the core concrete,but because it was in a strongly constrained area,the volume expansion was not as obvious as the sandwich concrete.The CFRP tube began to generate hoop tensile stress,which makes the core concrete less prone to large volume expansion.At this time,due to the bending deformation of the specimen,concrete appeared lateral micro-cracks in the tensile section of the middle section.As shown in Fig.6c,when the loading progress continued,the bearing capacity of specimen declined and the deformation increased,the buckling of steel tube in the compression zone becomes significantly larger,and the nearby concrete was crushed.The transverse cracks of the concrete in the tension zone have already begun to extend into the core concrete through the CFRP tube,which caused a part of the core concrete to be in tensile failure state.The CFRP tube also failed to withstand lateral tension and caused fiber bundles separation and cracking began.At the end,the core concrete in the compression zone continued to undergo volume expansion due to cracks,which caused the nearby constrained fibers to not withstand corresponding deformation and break.At this time,the corresponding load was defined as the failure loadNbe.
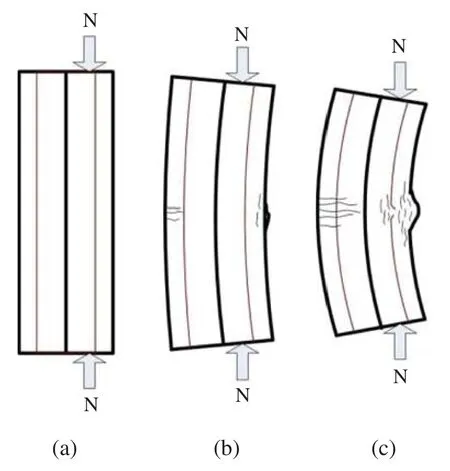
Figure 6:Failure process of specimen
According to the loading process of the HCFST-CFRP tube short column under bi-axial bending,the load (N)-deflection (μm) relationship curve can be divided into four sections:OA section (elastic stage),AB segment (elastoplastic phase),BC short (falling segment).Point D on the curve indicates that the CFRP suddenly broke,as shown in Fig.7.

Figure 7:Typical load-deflection curve
3.5 Stress Analysis
3.5.1 Stress Analysis of Concrete Core
The specimens ES52 series with different eccentricity were considered.As the bearing capacity of specimen attained peak load,the longitudinal stresses distributions of concrete are shown in Fig.8.For the confinement effect of CFRP tube,when eccentricity ratio is small or zero,concrete stresses are under compressive state.The stress of inner concrete is greater than concrete cubic strength (fc).The mechanism of inner concrete is enhanced and the longitudinal stress distribution of inner concrete and sandwich concrete is discontinuous.As the eccentricity increases,the range of compressive stress is narrower,tensile stresses appears,and the ultimate bearing capacity decreases.
Fig.9 shows the longitudinal stress distribution of the concrete when the column reaches the ultimate bearing capacity.It can be seen from the Fig.9 that as the eccentricity increases,the area of the concrete tension zone gradually increases,the area of the compression zone gradually decreases,and the maximum compressive stress continues to increase.
3.5.2 Stress Analysis of Steel Tube
Fig.10 shows the Mises stress distribution of the steel tube.It can be seen from the Fig.10 that when the load is small (Point A),the full section of the steel tube is basically in the elastic stage,and the stress distribution at the flat plate and the corner area is relatively uniform.When the ultimate bearing capacity (Point B) is reached,the whole section enters plasticity.The stress at the corner area reaches the maximum.
3.5.3 Stress Analysis of CFRP Tube
Fig.11 shows the maximum principal stress distribution of the CFRP tube in the process of loading.Its shows that the distribution of the maximum principal stress of the CFRP tube is uneven when the load was small (Point A),and the maximum value does not exceed 485 MPa,there is basically no confinement on the inner concrete.When the load reaches the ultimate bearing capacity (Point B),the maximum principal stress of CFRP tube reached 1404 MPa.At this time,the maximum tensile stress of the CFRP tube is not distributed in the middle section of the specimen.As the load continues to increase (Point C),the maximum principal stress begins to converge towards the middle section of the CFRP tube,and the maximum principal stress value reaches 2325 MPa.As the load continued to increase,the maximum principal stress increased until the CFRP can not withstand the volume expansion of the inner concrete and fracture.Fig.12 shows the distribution of the principal stress vector of the CFRP tube.It can be seen that the maximum principal stress direction is the tangential direction along the circumferential direction.
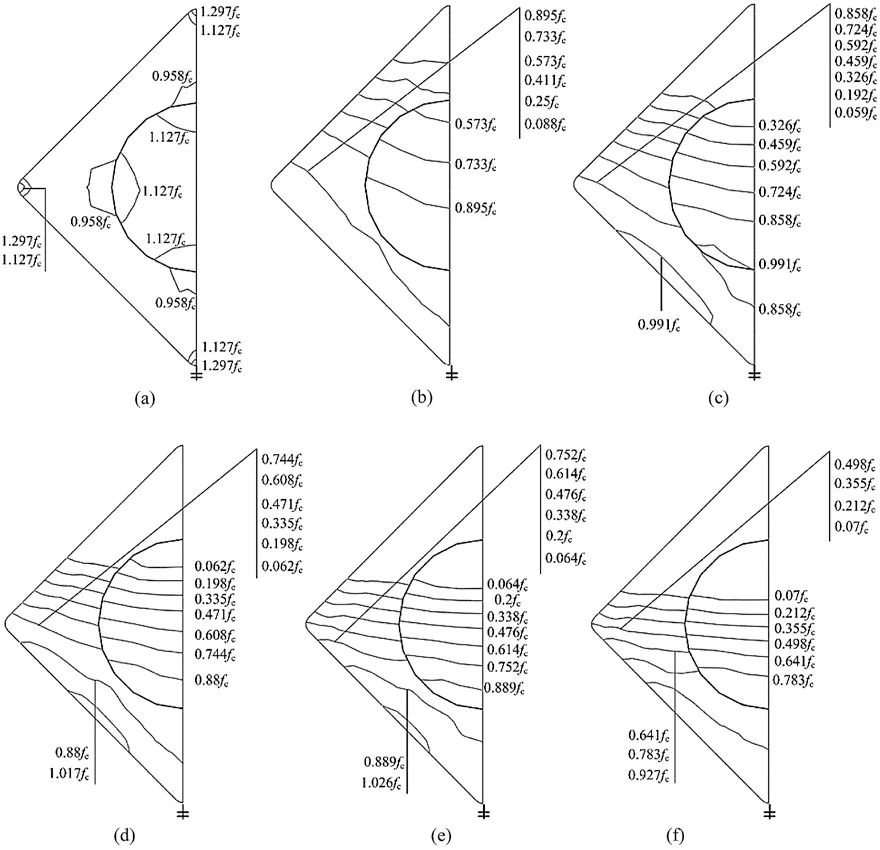
Figure 8:Longitudinal stress distribution of concrete at mid-height (a) ES52-0,(b) ES52-1,(c) ES52-2,(d) ES52-3,(e) ES52-4,(f) ES52-5
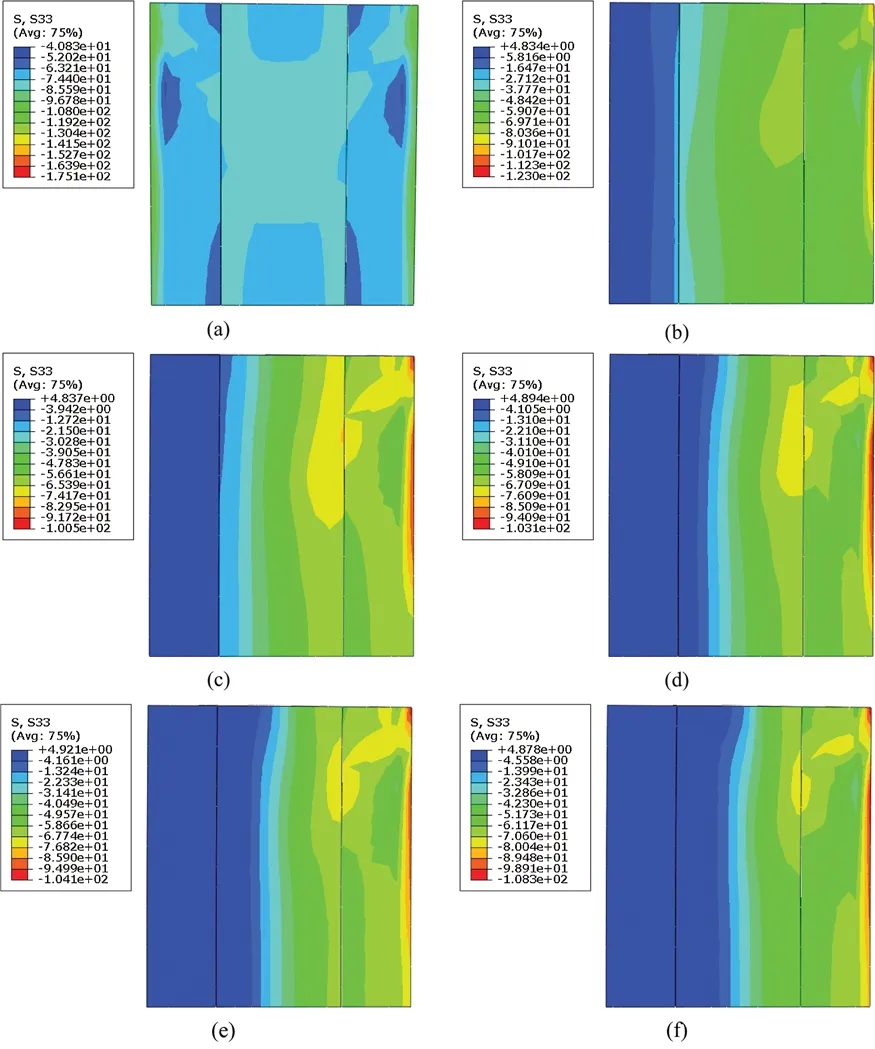
Figure 9:Longitudinal stress distribution of concrete at B point (a) AS52,(b) ES52-1,(c) ES52-2,(d) ES52-3,(e) ES52-4,(f) ES52-5
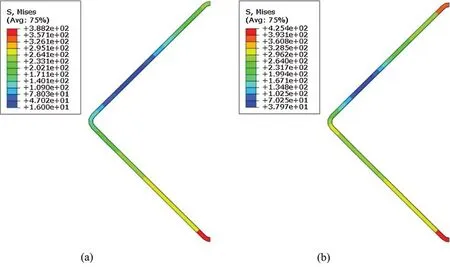
Figure 10:Mises stress distribution of steel tube at mid-height (a) Point A,(b) Point B
4 Parameters Analysis
Based on the results of finite element analysis,the influence of CFRP ratio and eccentricity on the behavior of HCFST-CFRP tube under biaxial eccentric compression was analyzed.Fig.13 shows the load-deflection curve of different CFRP ratio and eccentricity.It can be seen from Figs.13a–13c that the CFRP ratio has little effect on the ultimate bearing capacity of members,but it can increase the later bearing capacity of the member with a growth rate of 8.2% to 15.8%,which improves the ductility of member.The Fig.13d shows that the ultimate bearing capacity of the member reduced as the eccentricity increase,and the fracture of CFRP is delayed.
5 Calculations of Ultimate Bearing Capacity
The CFRP began to affect the mechanism of HCFST-CFRP stub column after ultimate bearing capacity,therefore,the compressive strength of CFRP can be negligible compared with steel and concrete.So,it is found that inner CFRP tube is helpless for enhancement of ultimate bearing capacity of HCFST-CFRP stub column.Based on the research on CFST stub column,Han [21] gives following formula as calculation for ultimate bearing capacity of CFST.


Figure 11:The maximum principal stress distribution of the CFRP tube (a) A point,(b) B point,(c) C point,(d) D point

Figure 12:The distribution of the principal stress vector of the CFRP tube,(a) B point,(b) C point
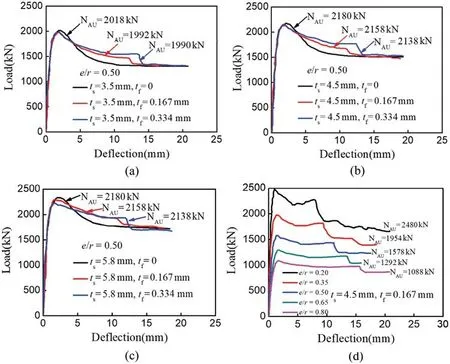
Figure 13:The load-deflection of different parameters (a) ts=3.5 mm,(b) ts=4.5 mm,(c) ts=5.8 mm,(d) e/r
Considered the loading position is on the plane of symmetry,the formula is simplified as following:

where,Mux=Muy=
Based on the parameter of specimen ES52,FEM was used to drawN/Nuvs.M/Mucurves,as shown in Fig.14.The FEM results indicate that ultimate bearing capacities between HCFSTCFRP and CFST stub column are approximate,and in agreement with the test results.After a great deal of calculations,Fig.14 shows that FEM results are mostly on left of curve drawn based on Eq.(3).It is safe that the formula studied by Han [21] is used to calculate ultimate bearing capacity of HCFST-CFRP stub column.
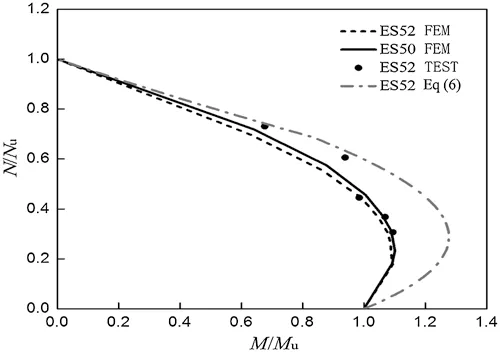
Figure 14:N/Nu vs. M/Mu interaction curves
6 Conclusions
(1) The CFRP ratio contributed little to the ultimate bearing capacity of HCFST-CFRP tube column under biaxial eccentric compression and can be ignored.The failure modes of HCFST-CFRP tube and CFST specimens were similar;the local buckling appeared at the mid-height of steel tube.
(2) The mechanical behavior of inner concrete could be improved by CFRP,then longitudinal stress distribution of innermost concrete and sandwich concrete were discontinuous.Ductility of HCFST-CFRP stub columns was better than HCFST.
(3) Confinement effect of CFRP tube to inner concrete mainly began to take effect after steel tube buckled.This is due to enhancement of ductility of HCFST-CFRP stub column.The ultimate bearing capacity of specimen decreased with the increasing of eccentricity.
(4) The formula is suited and safe to calculate the ultimate bearing capacity of HCFST-CFRP stub column under biaxial eccentric compression.
Funding Statement:This research was funded by Key Projects of National Natural Science Foundation of China (51938009),National Natural Science Foundation of China (51878419) and(51808353).
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- Redefined Extended Cubic B-Spline Functions for Numerical Solution of Time-Fractional Telegraph Equation
- Maximum Probabilistic and Dynamic Traffic Load Effects on Short-to-Medium Span Bridges
- Alcoholism Detection by Wavelet Energy Entropy and Linear Regression Classifier
- Number Entities Recognition in Multiple Rounds of Dialogue Systems
- Dynamic Pricing Model of E-Commerce Platforms Based on Deep Reinforcement Learning
- Peridynamic Modeling and Simulation of Fracture Process in Fiber-Reinforced Concrete
