土石坝溃决人员生命损失评估方法研究

胡 亮，钟 启 明，陈 亮

(1.河海大学 土木与交通学院，江苏 南京 210098； 2.南京水利科学研究院，江苏 南京 210029； 3.水利部土石坝破坏机理与防控技术重点实验室，江苏 南京 210029)

大坝溃决是一种低概率高风险的灾害。据水利部大坝安全管理中心统计[1]，我国共有水库98 460座，1954～2019年，共有3 541座大坝发生溃决。随着大坝除险加固工作的深入开展和安全管理水平的提高，我国溃坝事故明显减少。统计资料显示[1]：2000～2019年，我国共溃坝84座，年均溃坝4.2座，年平均溃坝率0.4×10-4，已明显低于世界年平均溃坝率(2.0×10-4)，与日本等发达国家的溃坝率接近(日本年平均溃坝率0.4×10-4)，标志着我国已进入低溃坝率国家行列。但近年来极端气候频发、地质运动加剧导致大坝出险事故频发，甚至发生溃坝。如2018年汛期，新疆射月沟水库大坝和内蒙增隆昌水库副坝发生溃决，给下游人民生命安全带来重大威胁。为完善大坝风险管理体系，减少大坝溃决造成的生命损失，作为大坝风险管理体系的重要组成部分，建立可靠的生命损失评估方法显得尤为必要。

1 国内外研究现状

为研究大坝溃决生命损失规律，构建大坝溃决损失评价指标体系，建立生命损失评估方法，协助大坝风险决策制定，国内外许多研究人员对大坝溃决损失进行了研究。但由于致灾环境复杂，生命损失受到定性与定量因素的耦合作用，造成致灾因子体系的不确定性与灰色性，使得生命损失难以定量评估。目前国内外的评估方法总体可分为3类：① 基于数理统计与回归分析的方法，这类模型操作简单但依赖使用者的风险管理经验，评估精度不足；② 通过物元对比分析建立标准物元集的方法，这类模型很大程度上依赖于标准物元集的数据均匀性，但尚未解决不同参数量化过程统一的问题；③ 结合概率论与可靠度等方法建立的动态分析方法，这类方法理论上是最能描述生命损失过程机理的评估方法，但由于研究起步较晚，对于生命损失过程中的各评价指标阈值的选取还有待深入研究。表1给出了国内外目前常用的溃坝生命损失评估方法。

本文基于前人的研究成果，同时广泛调查分析了有实际溃坝生命损失统计数据的案例，开展生命损失评估影响因子的研究，将影响因子分为主要影响因子和次要影响因子，构建了各影响因子的定量分析方法。在此基础上建立了生命损失评估方法，为溃坝生命损失评估提供定量化的分析方法。

2 生命损失评估影响因子分析

在溃坝风险体系中，最为重要的是研究生命损失与承灾体、致灾因子之间的关系，风险人口是溃坝损失的主要承灾体，也是生命损失致灾因子的直接作用对象。致灾因子是指自然或人为环境中，能够对人类生命产生不利影响的事件，根据影响因素对生命损失的影响程度的强弱可分为主要影响因子与次要影响因子。

2.1 主要影响因子分析

通过借鉴Graham、周克发等人的研究成果，将主要影响因子选定为：警报时间、溃坝洪水严重性、风险人口对溃坝理解程度与风险人口密度等四大因素。

2.1.1警报时间

警报时间(WT)是生命损失影响的重要因素，警报时间的长短直接影响着风险人口的撤离与风险决策的制定。目前对于警报时间还没有较为统一的定义，较为常用的有3种(如图1所示)：一是警报时间发布至洪水到达风险人口原所在地的时间段[5]；二是风险人口接受到警报至洪水到达风险人口原所在地的时间段[17]；三是风险人口接受警报至洪水到达风险人口所在地的时间段[19-20]。第三种定义综合考虑了风险人口疏散的动态过程，无疑更贴近现实情况，但鉴于统计资料的局限性，本文选取第二种警报时间的定义。

图1 警报时间定义概念Fig.1 Alarm time definition

表1 国内外常用溃坝损失评估方法对比Tab.1 Comparison of commonly used dam break loss assessment methods at domestic and abroad

2.1.2溃坝洪水严重性

溃坝洪水严重性(SD)为洪水对居民与建筑物等破坏程度的参数，也是造成风险人口死亡的直接因素，溃坝洪水的强弱与坝型、库容、溃坝模式、下游地形等因素有关，一般以某计算断面的洪水水深与洪水流速的函数关系表示为[5]

SD=D×V

(1)

式中：D为水深，m；V为流速，m3/s。

溃坝洪水的破坏机理主要包括3个部分：洪水水深、流速以及洪水上升速度。主要的作用体现在对房屋建筑的破坏及人在水中的活动稳定性、机动性等方面。本文基于国内外常用的经验方法将洪水等级分为5个等级(见表2)[5，21]。

表2 洪水等级划分Tab.2 Classification of flood levels

2.1.3风险人口对溃坝理解程度

风险人口对溃坝事件的理解程度(UD)在很大程度上影响着生命损失的大小，风险人口的理解程度主要包括对洪水警报的信任，对逃生必要性、措施、路径的认识，对洪水可能的淹没范围等情况的了解。理解程度的研究是对个体风险研究的重要因素，这些因素与政府的宣传组织和群众受教育程度等有关。

本文基于前人研究经验，按照风险人口对溃坝洪水理解人数占比将理解程度分为5个等级(见表3)[7]。

表3 理解程度等级划分Tab.3 Classificationof of understanding levels %

2.1.4风险人口密度

风险人口密度(DP)是指风险人口总数PAR与淹没区域面积S之比：

DP=PAR/S

(2)

风险人口密度影响着人员应急疏散及抢险救援等应急救援行动，风险人口密度越大越不利于人员的应急疏散与抢险避险工作的落实。

前人已经对警报时间、溃坝洪水严重性与风险人口对溃坝理解程度等因子进行了较为广泛的研究，但对于风险人口密度对溃坝生命损失的影响研究较少。通过对国内拥有调查资料的8个溃坝案例进行分析发现[5]，在警报时间、洪水严重性等参数条件相似的情况下，风险人口密度越大则相应的死亡率越高(如图2所示)。所以在建立评估方法时需考虑风险人口密度对生命损失的影响。

图2 人口密度与死亡率关系Fig 2 Relationship between population density and mortality

2.2 次要影响因素分析

与主要影响因素的影响作用相比，次要因素影响较弱且作用效果并不如主要因素清晰，但当次要因素在某些极有利或极不利状态下，对溃坝生命损失也有着不可忽略的影响。通过对已知因素进行分析，筛选出影响较大的7个因素建立次要因素集合。

(1) 溃坝时间。溃坝时间是指溃坝事故发生的时间，影响着警报时间的长短与风险人口理解程度，若溃坝发生在节假日或群众休息时间则由于人员聚集不利于群众应急避险，若溃坝发生在夜间，则不利于群众对于突发事故采取应急避险措施与分辨灾害情况与寻找避险路径[17]。

(2) 天气。天气影响着溃坝洪水的演进与风险人口的应急避险行为。在台风、暴雨天气中，警报率与撤离成功率都会大大降低。

(3) 与坝址距离。一般来说风险区距坝址距离越远，洪水严重性越低，警报时间越长。

(4) 应急预案。是否具备应急预案及其实施情况直接关系着死亡人口的数量。

(5) 坝高。坝高对于溃口洪水流量过程具有重要的影响，坝高越大，溃坝洪水具有的势能越大，溃口流量和流速也随之增大。

(6) 库容。库容决定着溃坝洪水的演进历程与淹没历时，库容越大，溃坝造成的洪水严重性越强，对下游风险区的破坏作用越强烈。

(7) 建筑易损性。建筑类型与坚固程度关系着风险人口的避难成功率。在高洪水严重性下，结构性差的房屋不仅不能为风险人口避难，反而会因为无法抵抗洪水而倒塌，导致人员伤亡。

3 生命损失评估模型

通过对具有统计资料的16座大坝溃坝数据进行统计分析，基于双对数坐标构建了风险人口与生命损失的函数关系。充分考虑警报时间、溃坝洪水严重性和风险人口对溃坝理解程度、风险人口密度等4个主要影响因素和溃坝时间、天气、与坝址距离、应急预案、坝高、库容、建筑易损性等7个次要影响因素，对建立的风险人口与生命损失的函数关系进行修正，建立了生命损失评估模型，并通过16座已溃大坝的生命损失数据对模型的合理性进行了验证。

3.1 模型函数关系

风险人口(PAR)是指溃坝洪水淹没范围内的人数，也是溃坝灾害的主要承灾体，参照经验定义风险人口为暴露在洪水深度大于0.3 m的居民[2]。本文通过对16座水库大坝的溃坝数据收集与分析发现[5-6]，风险人口与生命损失数据之间存在着一定的函数关系(见表4)，通过对数据进行拟合，构建了风险人口与生命损失的函数关系(如图3所示)。

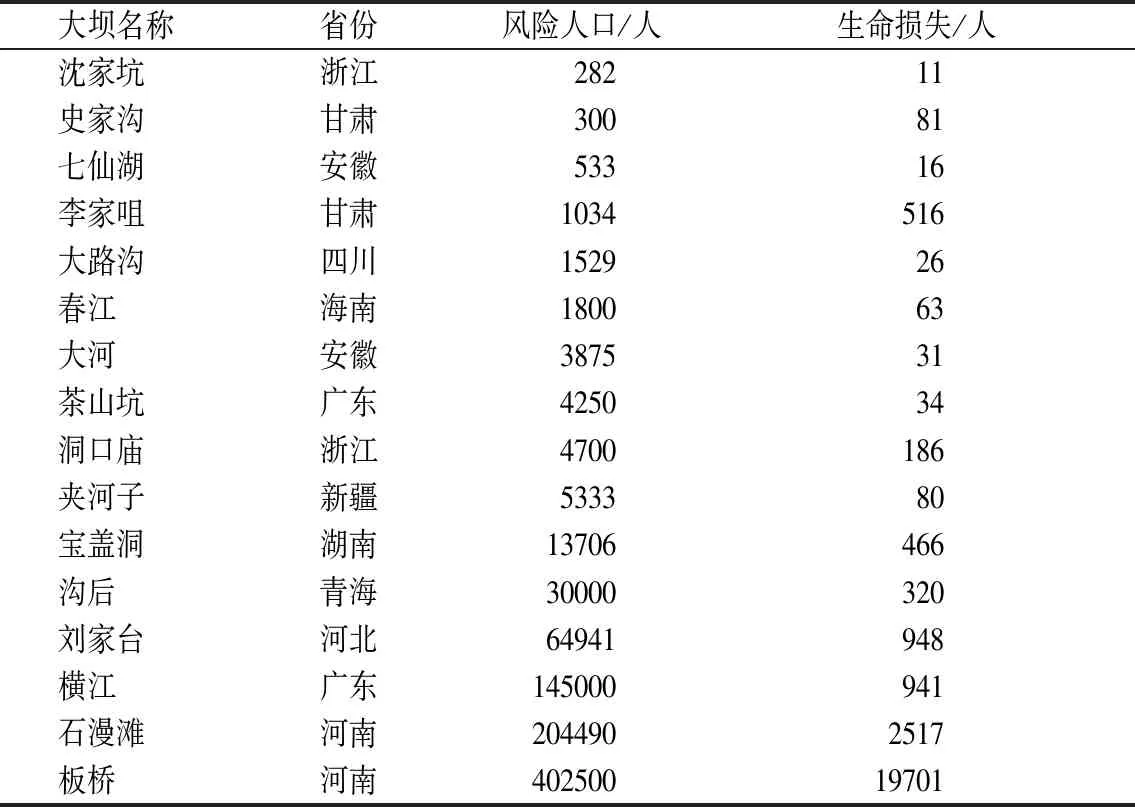
表4 16座大坝风险人口与生命损失统计值Tab.4 Statistics of population at risk and loss of life for 16 dams

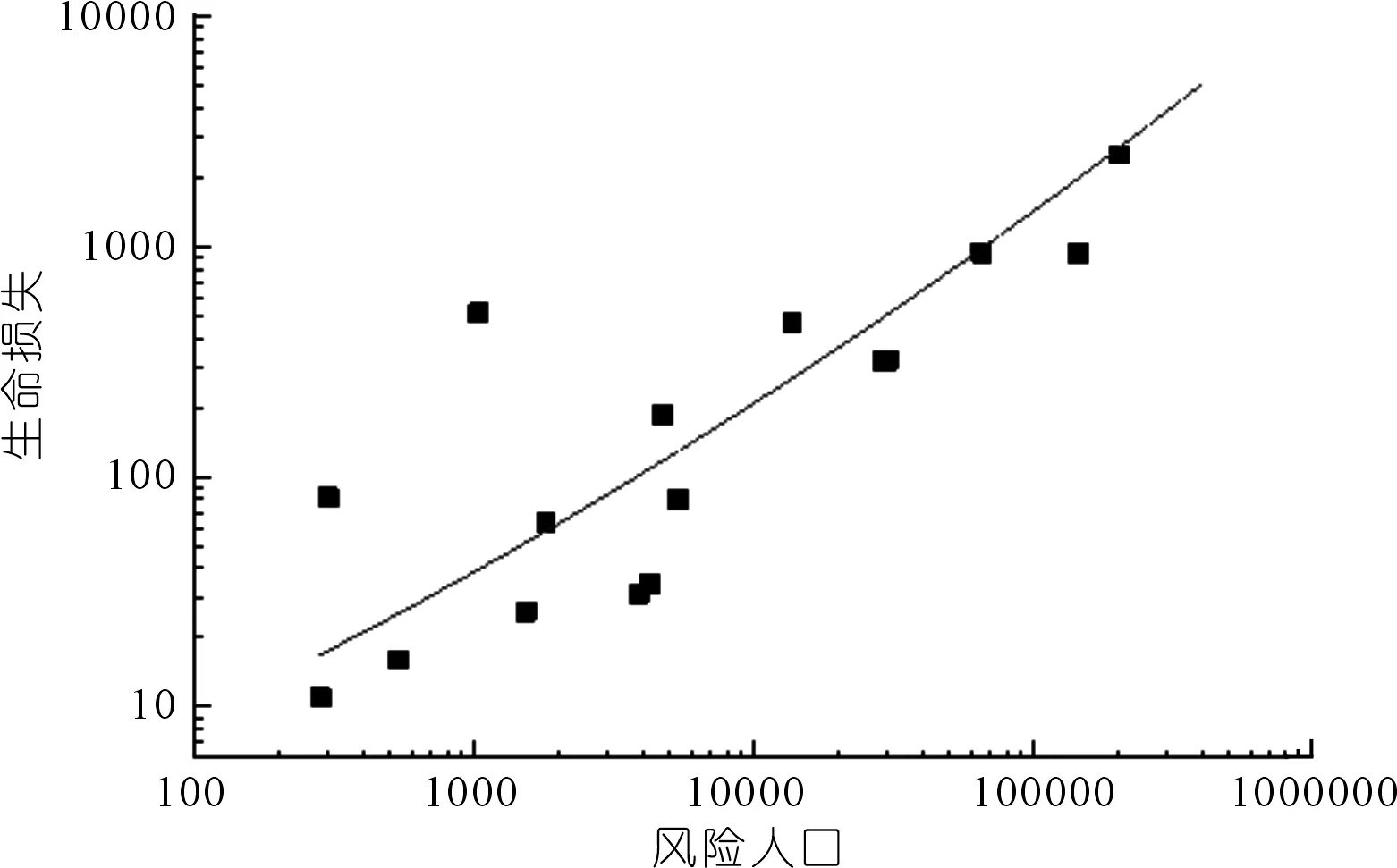
图3 风险人口与生命损失关系Fig.3 Relationship between risk population and loss of life

风险人口与生命损失的关系式：

(3)

式中：L为生命损失初步计算值；PAR为风险人口总数；A、B为常数，A的取值与人口密度DP有关(见表5)，B取0.06。

表5 常数A取值Tab.5 Suggested value for constant A

由于建立风险人口与生命损失关系式时已考虑了风险人口密度，因此在评价溃坝生命损失时还应考虑其他3个主要影响因子和7个次要影响因子，需要对式(3) 进行修正。通过修正将无法统一量化的参数用修正系数的形式体现，反映各影响因素对生命损失的影响程度，修正后的生命损失值函数表达式为

LOL=α·β·L

(4)

3.2 主要影响因素修正系数

在生命损失的主要因素中，风险人口密度已在式(3)中体现，作者建议的其他3个影响因素的修正系数取值见表6。

表6 主要影响因素修正系数取值Tab.6 Suggested values of correction factors for major influencing factors

3.3 次要影响因素修正系数

在评估生命损失时不仅仅需要考虑警报时间等主要因素的影响，还受到溃坝时间、天气、与坝址距离等因素的影响，这些因素的影响虽然没有主要因素的影响程度大，但这些因素在极不利或极有利的情况下对生命损失也有着重要影响。作者建议的次要因素修正系数取值见表7。

表7 次要因素修正系数取值Tab.7 Suggested values for the correction factors of minor factors

3.4 模型验证

为验证生命损失评估模型的合理性，对前述的16座已溃大坝的进行生命损失评估验算，计算结果见表8和图4。通过计算结果分析发现，有12组案例估算结果在±50%以内，占比75%；15组案例结果在±100%以内，占比94%；对4组估算结果在±50%外案例进行分析，4组案例实际损失人数均较少，对评估结果敏感性大，评估损失数与实际损失数相差在60人以内，平均误差值小，评估结果稳定，符合实际情况。计算结果表明本文建立的生命损失评估模型较为可信。

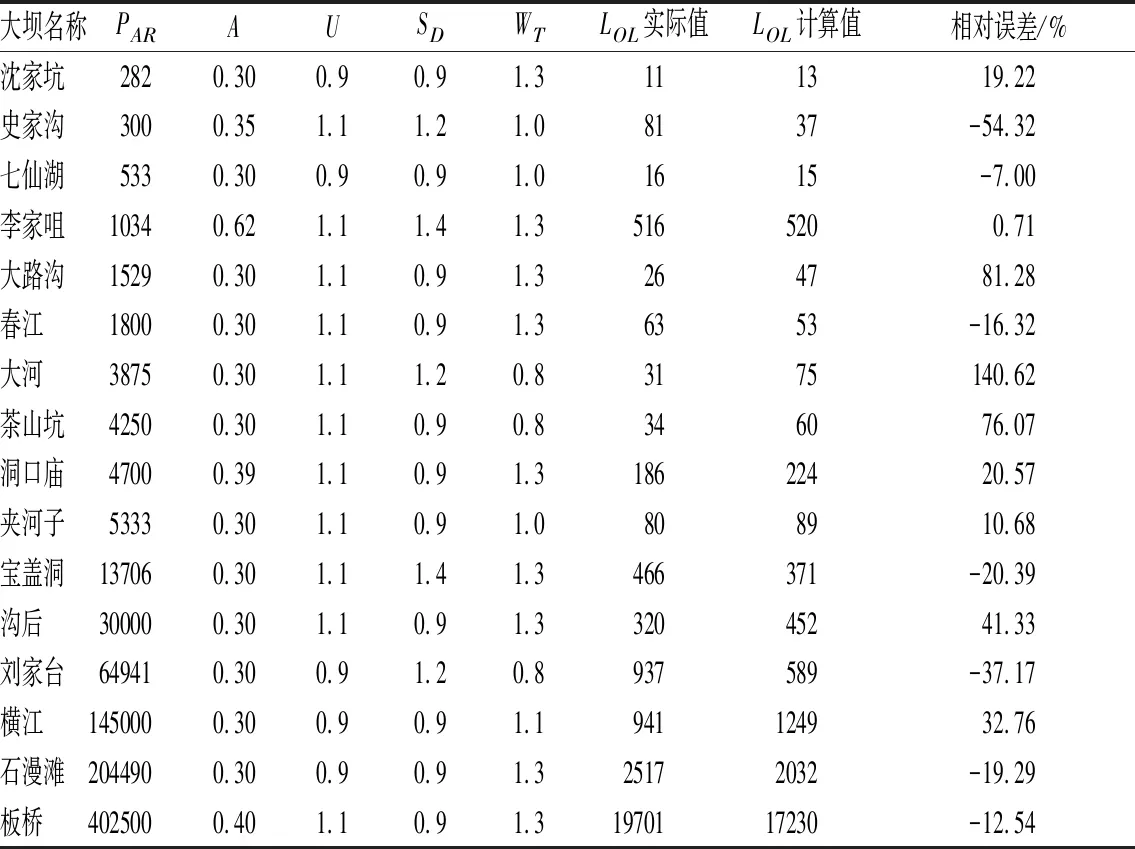
表8 案例验算结果Tab.8 Analysis of cases verification results

图4 案例验证结果对比Fig.4 Verification of model result by real dam break cases

4 模型应用

2018年7月31日，我国新疆哈密市沁城乡射月沟水库由于遭遇超标准洪水发生漫顶溃坝事故，导致下游二宫村头宫队与二宫队共16名群众死亡。由于此次溃坝事故发生年代较近，拥有完整可信的调查资料，为了进一步检验模型的适应性，采用本文建立的生命损失评估模型对此案例进行计算分析。

4.1 溃坝概况

新疆哈密市沁城乡射月沟水库位于沁城乡二宫村头宫队上游2 km处。射月沟水库工程正常蓄水位为1 492.53 m，设计洪水位1 494.57 m，校核洪水位1 496.43 m；射月沟水库总库容为677.90万m3，调洪库容219.93万m3[22]。射月沟水库大坝坝型为沥青混凝土心墙坝，最大坝高41 m[22]。

水库所在区域于2018年7月31日凌晨2：00开始降雨，5：00后雨量增大降暴雨，大量洪水涌入库区造成大坝漫顶破坏，10：15大坝左肩溃口形成，10：50溃坝结束，最终溃口如图5所示。由于溃坝洪水流量大，洪水流速快，冲击力强，导致下游发生人员伤亡。此次溃坝造成下游二宫村头宫队与二宫队共16名群众死亡。据调查，由于当时正值大雨，雨具缺乏，群众也不相信西北地区会有洪水来临，导致部分群众不愿撤离，甚至部分已经撤离群众不顾劝阻从高地返回，这也是导致人员伤亡的重要原因。

图5 从上游拍摄射月沟水库大坝最终溃口Fig.5 Final breach of the Sheyuegou Reservoir dam from the upstream

灾情发生后，当地政府迅速组织救援，出动解放军、武警、公安等力量共1 800余人参与救援，紧急转移安置5 583人。

4.2 溃坝洪水分析

采用参数模型和经验公式计算大坝漫顶溃决后的溃口峰值流量与洪水演进后下游断面处的峰值流量，进而分析下游风险区的洪水淹没情况和严重程度。选取南京水利科学研究院开发的心墙坝漫顶溃坝参数模型[23]计算射月沟水库溃坝时的溃口峰值流量，模型主要输入参数见表9。同时选取下游群众聚居地(头宫队和二宫队)处的断面，采用经验公式计算洪水特征[24]，其中，头宫队和二宫队分别位于坝址下游2 km和6 km处。

表9 射月沟水库溃坝模拟主要参数Tab.9 Main parameters of dam break simulation of Sheyuegou Reservoir

对于溃口峰值流量采用(5)式计算[23]：

(5)

式中：QM为溃口峰值流量；Vw为水库库容；g为重力加速度，取9.8 m/s2；hw为溃坝水深；hd为坝高；hb为溃口深度；h0为单位坝高，取1 m。

由式(5)得出射月沟水库溃坝时溃口的峰值流量为4 856.1 m3/s，这与新疆自治区相关部门开展的洪水调查获得的溃坝洪水峰值流量为4 304 m3/s的结论基本一致，相对误差为12.8%。

对于下游断面处的洪水峰值流量，可采用(6)式计算[24]：

(6)

式中：QLM为距离坝址Lm处的洪水峰值流量；L为距坝址距离；k为经验系数，其中，山区取1.1～1.5，丘陵地区取1.0，平原地区取0.8～0.9[24]，本文取k=1.0；v为断面处的洪水平均流速，其中，山区一般取3.0～5.0 m/s，丘陵地区取2.0～3.0 m/s，平原地区取1.0～2.0 m/s[24]，本文取v=2.0 m/s。

将式(5)的计算成果代入式(6)计算下游断面峰值流量，获得坝址下游2.0 km(头宫队)处的洪水峰值流量为2 829.5 m3/s，坝址下游6.0 km(二宫队)处的洪水峰值流量为1 542.2 m3/s。洪水的淹没情况和头宫队、二宫队居民点示意图见图6～8。

对于风险区洪水严重程度，除式(1)的计算方法外，也可采用(7)式计算：

(7)

式中：w表示淹没断面平均宽度。

通过测量发现，下游2 km(头宫队)处断面的平均宽度为400 m，计算得出洪水严重性SD为7.1 m2/s，依据表3可得，洪水严重程度为较高；下游6 km(二宫队)处断面的平均宽度为400 m，计算得出洪水严重性SD为3.9 m2/s，依据表3可得，洪水严重程度为较低。

图6 洪水淹没范围Fig.6 Flooded area

图7 头宫队地图Fig.7 Map of the Tougongdui resident site

图8 二宫队地图Fig.8 Map of the Ergongdui resident site

4.3 生命损失评估

通过调查确定坝址下游二宫村头宫队与二宫队风险人口总数为440人(其中头宫队234人，二宫队206人)，实际死亡人数16人，淹没面积2.4 km2，人口密度184 人/km2。警报时间较为充分(WT为0.8 h)，群众理解程度为“模糊”。洪水强度通过计算得到头宫队处洪水强度为7.1 m2/s，强度等级为较高；二宫队处洪水强度为3.9 m2/s，强度等级为较低。由于溃坝发生在上午，群众应急反应能力较强。溃坝时正值强降雨，不利于人员避难与警报传递。大坝溃决后，当地政府迅速组织救援，紧急疏散大批群众，极大减小了人员损失。其余影响因素参数不详者均取为1.0，具体参数取值见表10。

表10 模型计算参数取值Tab.10 Model calculation parameter value

对于二宫队，同理可得：L=10A·lgPAR+B·(lgPAR) 2=8；主要影响因素修正系数α=0.792，次要影响因素修正系数β=0.891，将L和α、β代入式(4) 可得：LOL≈6人。

通过计算得到头宫队与二宫队的死亡人数为16人，与实际情况相符。

另外，选择国内外常用的其他模型与本文模型的计算结果进行比较，其他模型的表达式和参数见表2，各模型的计算结果对比情况见表11。

表11 各模型计算结果对比Tab.11 Comparison of calculation results of each model

通过各模型计算结果的对比发现，本文模型可较好地评估新疆射月沟水库溃坝案例的生命损失情况，表明本文模型的适应性和可靠性。

5 结 语

基于国内外生命损失评估模型研究现状的评估，并通过对16座已溃大坝生命损失的调查与分析，确定了生命损失评价指标，明确了各影响因素的定义与作用机理，在此基础上提出了一个新的生命损失快速评估方法。通过案例验证与新疆射月沟溃坝案例的反馈分析验证了模型的合理性。另外，通过与国外其他模型的对比分析发现，本文所提的方法具有评估过程简单、准确率高等优点，且在次要因素未知的情况下依旧有较好的评估结果。