基于PCA-HUP模型的洪水预报不确定性分析
——以信江流域梅港站为例
2021-04-27冻芳芳,刘沁薇,王淑梅,刘建伟
冻 芳 芳,刘 沁 薇,王 淑 梅,刘 建 伟
(1.江西省水文局,江西 南昌 330000; 2.江西省上饶市水文局,江西 上饶 335100)
水文模型应用于洪水预报时,除了水文过程本身固有的自然不确定性外,还存在模型输入、模型参数和模型结构的不确定性,这些不确定性的存在必将导致洪水预报成果存在不确定性[1-3]。关于如何定量描述洪水预报成果不确定性的研究一直是水文领域的热点。纵观国内外关于洪水预报不确定性分析的研究,大体上可以分为基于不确定性要素耦合途径和基于预报总误差分析途径两类[4]。不确定性要素耦合途径的实质是分析预报过程中各环节的主要不确定性因子,估计其概率分布,再将这些不确定性耦合到洪水预报模型中,从而量化预报成果的不确定性[5-8];预报总误差分析途径不直接处理模型输入数据、模型结构和参数的不确定性,代之以处理其综合误差(即终端输出误差),算法上不依赖于具体的水文预报模型,可以与任何模型相耦合,最终以后验分布的形式直接提供模型输出变量概率分布的估计,量化洪水预报成果的不确定性[4,9-10]。
水文不确定性处理器(HUP)是预报总误差分析方法的一种,被广泛应用于洪水预报不确定性分析中[11-14]。针对采用最小二乘法估计HUP模型参数过程中存在的多重共线性问题,Yao等[15]提出采用主成分分析技术(PCA)对传统HUP模型进行改进,避免了HUP模型中似然函数求解过程中的多元共线性问题。
本文以江西省信江流域梅港水文站为研究对象,采用PCA-HUP模型分析洪水预报不确定性,在提供类似于传统定值预报结果的同时,可实现预报成果的不确定性定量评估,为进一步提升信江流域防洪减灾决策的科学水平提供技术支撑。
1 方法原理
1.1 HUP基本理论
设H0为预报时刻已知的实测流量,Hn,Sn(n=0,1,2,…,N)分别为待预报的实测流量、确定性水文模型的预报流量,估计值分别用hn,sn表示,N为预见期的长度。根据贝叶斯原理及任意的观测值H0=h0,在Sn=sn的条件下,可求得Hn的后验密度函数[10-11]:
(1)
式中:hn为Hn的估计值;sn为Sn的估计值;h0为预报时刻已知的实测流量;fn为Hn的似然函数;gn为先验密度函数。
预报量后验分布函数的形式复杂,为了简化计算及推求预报量后验分布的解析解,一般先通过正态分位数转换将非正态的流量序列分布转换为亚高斯分布,在正态空间中对先验分布式和似然函数式进行线性假设,并采用最小二乘法对相关参数进行估计[11]。
令Q表示标准正态分布,q表示相应的标准正态密度函数,则Hn与Sn转换后的正态分位数可分别表示为
Wn=Q-1(Γ(Hn)),n=0,1,2,…,N
(2)
(3)

在获得Hn和Sn的正态分位数Wn和Xn后,通过假定转化空间中的流量过程服从一阶马尔可夫过程的正态-线性关系,构造了如下的先验分布函数:
Wn=cWn-1+G
(4)
式中:c为参数,G为不依赖于Wn-1的残差系列,且服从N(0,1-c2)的正态分布。
通过假定正态空间中的各变量Xn,Wn,W0服从正态-线性关系,构造了如下的似然函数:
Xn=anWn+dnW0+bn+Θn
(5)

在正态空间中,进一步推出Wn的后验密度函数:
(6)
(7)
通过下式可获得原始空间中预报流量的分布函数为
(8)
根据公式(8)预报流量的分布函数,可计算任一分位点的预报值,如50%概率对应的中位数预报及90%置信度对应的预报区间(5%概率和95%概率对应的分位数组成的区间)。
1.2 PCA-HUP模型
由先验分布(式(4))可以看出,似然函数(式(5))中的自变量Wn和W0之间存在明确的线性关系,会导致公式(5)存在多重共线性问题。采用传统最小二乘法进行参数估计,会使得估计的回归系数不唯一,导致回归方程不稳定。因此,Yao等[15]采用主成分分析技术(PCA)对传统HUP模型参数估计方式进行了改进。
主成分回归的基本思想是对原始回归变量进行主成分分析,将线性相关的自变量转化为线性无关的新综合变量,采用新综合变量建立模型回归方程。针对变量Wn和W0。考虑它的线性变换:
(9)

Xn=bn+b1Z1+b2Z2
(10)
由于各个主成分之间是相互独立的,为此可采用最小二乘法估计公式(10) 中的参数bn,b1和b2,进而克服了自变量间的多重共线性问题。
将公式(9)带入到公式(10)中,公式(5)可进一步表示为
(11)
即,an=b1a11+b2a12,dn=b1a21+b2a22
3 应用研究
梅港水文站为信江流域主要控制站,位于信江下游余干县梅港乡。梅港水文站集水面积15 535 km2,占信江总流域面积的97.4%。1952年4月设站,有流量、水位、降雨量、蒸发量、含沙量等测验项目。实测最高水位为1998年的29.84 m(吴淞基面),实测最大流量为2010年的13 800 m3/s。本研究中,采用2012~2019年共10场洪水资料对PCA-HUP模型进行率定验证,其中2012~2017年的8场洪水用于模型率定,而2019年的2场洪水用于模型验证。场次洪水的确定性预报值是通过新安江模型预报获得。
图1给出了实测系列和模型预报系列的经验累积分布函数及三参数对数威布尔分布函数的拟合效果图。从图1可以看出,三参数对数威布尔分布函数能很好地拟合实测系列和模型预报系列。

图1 实测系列和模型预报系列的拟合效果Fig.1 Fitting effect of the measured series and prediction model series
表1给出了基于PCA-HUP模型的率定期8场洪水的分析结果,并与原始预报成果进行了对比分析。其中,PCA-HUP模型的确定性系数和洪峰相对误差指标值是基于PCA-HUP模型提供的中位数(Q50)预报结果计算获得,而离散度和覆盖率指标值是基于PCA-HUP模型提供的90%置信度下的预报区间计算获得。

表1 基于PCA-HUP模型的预报评估结果(率定期)Tab.1 Evaluation results of flood forecast based on PCA-HUP Model(rate period)
从表1中的中位数(Q50)预报结果来看,就确定性系数指标而言,8场洪水的确定性系数指标值均为0.99,高于原始预报的平均确定性系数为0.92;就洪峰相对误差指标而言,8场洪峰的相对误差绝对值的平均值为0.40%,远小于原始预报的6.23%。在分析的8场洪水中,经PCA-HUP模型处理后,8场洪水的确定性系数均增大,且洪峰相对误差均减小,表明经PCA-HUP模型处理后,洪水预报精度整体上有明显的提高。从90%置信度下的预报区间来看,就离散度指标而言,其值在0.20~0.21之间,平均值为0.20;就区间覆盖率指标而言,其值在91%~100%之间,平均值达97%。在离散度较小情况下,保证了较高的覆盖率。
图2给出了率定期2场洪水的实测值、原始预报、概率预报模型的中位数预报(Q50)及90%置信度下的区间预报成果。从图2中可以看出,90%置信度的预报区间很好地描述了洪水预报的不确定性,且覆盖了绝大多数的实测点据。
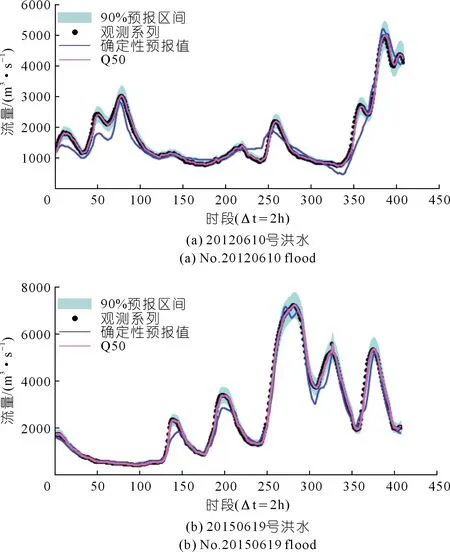
图2 率定期2场洪水的PCA-HUP模型预报成果Fig.2 Forecast results of PCA-HUP model of two floods in rate period
表2给出了基于PCA-HUP模型的验证期2场洪水的分析结果,并与原始预报成果进行了对比分析。从表中可以看出,就中位数(Q50)的预报结果而言,2场洪水的确定性系数值均为0.99,高于原始预报的平均确定性系数0.91;而2场洪峰的相对误差绝对值的平均值为0.28%,远小于原始预报的7.15%。就90%置信度下的预报区间而言,2场洪水的离散度均值为0.20;而区间覆盖率的均值为0.98。与率定期结果相似,在离散度较小情况下,保证了较高的覆盖率。

表2 基于PCA-HUP模型的预报评估结果(验证期)Tab.2 Evaluation results of flood forecast based on PCA-HUP Model(verification period)
图3给出了验证期2场洪水的实测值、原始预报、概率预报模型的中位数预报(Q50)及90%置信度下的区间预报成果。从图中可以看出,90%置信度的预报区间同样很好地描述了验证期2场洪水的预报不确定性,且覆盖了绝大多数的实测点据。
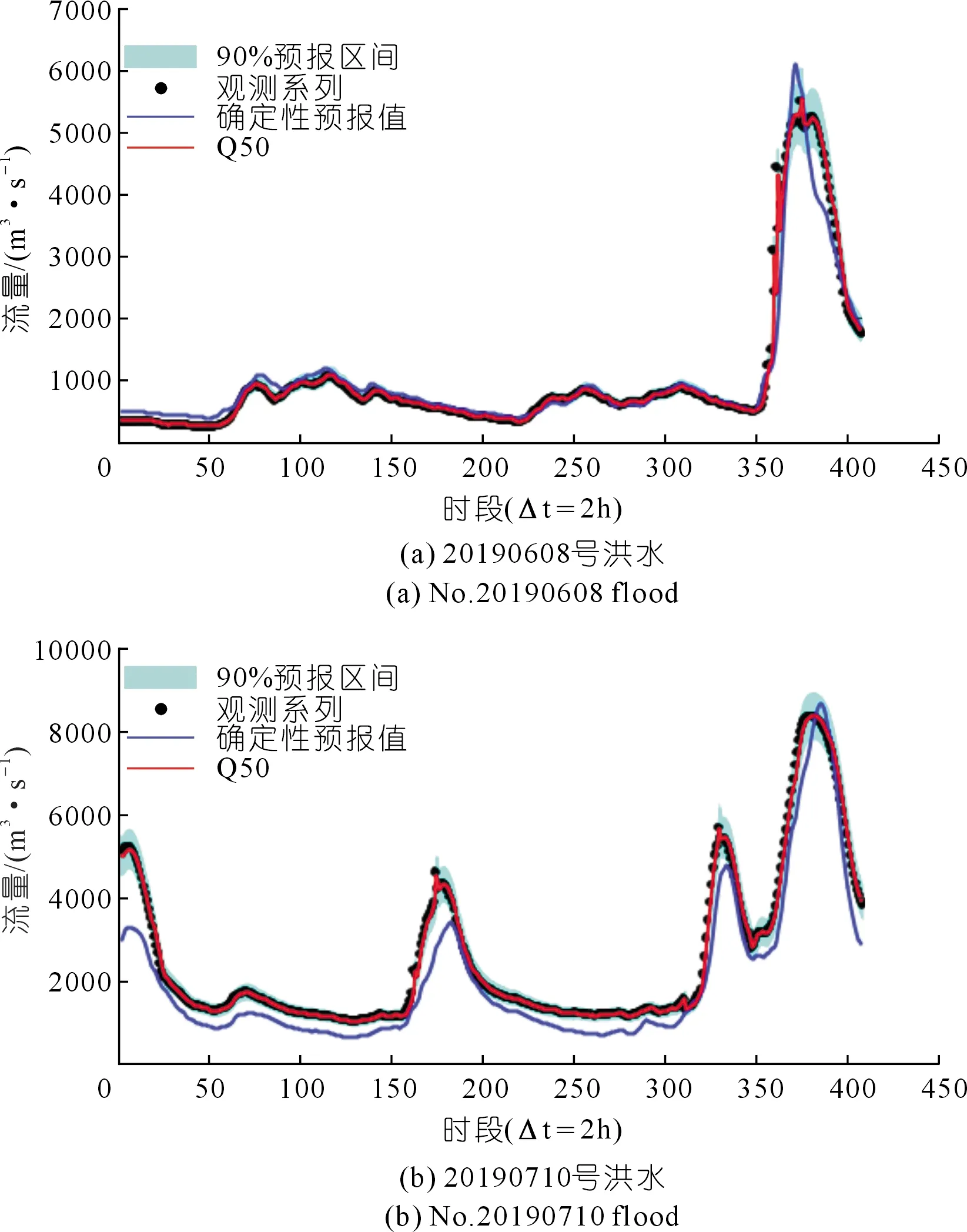
图3 验证期2场洪水的PCA-HUP模型预报成果Fig.3 Forecast results of PCA-HUP model of two verification periodic floods
4 结 论
以信江流域梅港站为例,采用PCA-HUP模型对洪水预报不确定性进行了分析,在提供中位数(Q50)定值预报结果的同时,也提供了90%置信度下的预报区间成果。主要结论如下:
(1) 基于确定性系数指标和洪峰相对误差指标,评估了原始确定性模型预报精度和PCA-HUP模型的中位数(Q50)预报精度。结果表明:无论是在率定期还是在验证期,PCA-HUP模型的确定性系数平均值均高于原始预报的确定性系数平均值。经PCA-HUP模型处理后,洪水预报精度整体上有明显的提高。
(2) 基于离散度和覆盖率指标,评估了PCA-HUP模型计算的90%置信度预报区间的可靠性。结果表明:率定期和验证期10场洪水的覆盖率均在90%以上,且离散度均在0.20左右,具有较高的可靠性。
