1951-2018年华南前汛期暴雨特征分析——以韶关市为例

周嘉琦, 陈世发

(韶关学院 旅游与地理学院， 广东 韶关 512005)

随着全球气候变暖，气候异常事件明显增多，各地极端降水事件频现，暴雨是我国常见的气象灾害之一，其特点是长时间、强度大，导致洪涝灾难的发生，对人们生命安全和生产、生活安全带来非常大的危难[1-3]。因此，重视暴雨观测、研究暴雨特点，是气象灾害预防工作的基础。

国内外学者们对暴雨气候特征进行了相关研究，Barredo[4]研究表明，1970—2005年欧洲的暴雨灾害加重的主要原因不是气候异常，是人口暴增而导致脆弱性增加的结果。广东前汛期降水为全年降水量的40%～60%，前汛期降水的多少直接影响到广东省汛期的旱涝[5-7]；艾卉等[8]从暴雨日数、暴雨强度和暴雨贡献率，分析广州汛期的暴雨的变化特征；李明华等[9]认为，惠州城区50 a的雨日气候特征应全面研究雨日及不同强度雨日的气候统计特征；凌良新等[10]认为，潮州市暴雨主要发生在4—9月，而且暴雨天气的发生时间有提前的趋势。虽然对不同区域的暴雨有所研究，但针对前汛期暴雨的研究相对较少。

华南地区是我国汛期最长的区域，暴雨气候有地域差异，对气候变化反映也不尽相同。为探讨前汛期(4—6月)不同等级暴雨变化的趋势、突变点和周期变化规律及重现期，本文选取韶关市1951—2018年的日降水资料目的在于探讨：(1) 韶关市前汛期暴雨、大暴雨事件变化特征及其与降水的关系；(2) 前汛期暴雨、大暴雨事件的周期变化规律；(3) 前汛期暴雨、大暴雨事件的重现期。本研究以期找出长时间前汛期不同等级暴雨的变化趋势和周期变化规律，有利于更加全面了解韶关市的气候变化特征，对于预测气候灾害，及防灾减灾有重大意义。

1 研究区概况与研究方法

1.1 研究区概况

韶关市处于广东省的北部，北江的中上游地区，对内连接珠三角，具有重要的经济、生态地位。山地丘陵地形显著且北部依靠南岭，气候属于中亚热带季风气候，季风气候明显，雨热同期，多年平均降水量为1 618.91 mm(1951—2018年)，降水丰富且集中，易发生涝灾、泥石流和滑坡等灾害。

1.2 数据来源与方法

1.2.1 数据来源 本文运用中国气象共享服务网提供的1951—2018年韶关市气象站降水资料(日降水量)，分别算出前汛期暴雨、大暴雨的频次和降水量，再通过Excel，SPSS，Origin，Matlab，Furfer等软件进行数据处理。

1.2.2 前汛期的确定和暴雨等级的方法 华南地区降水呈现双峰型特征，其中主峰为6月，次锋为8月。每年4—6月，华南地区受大型降水过程主要受冷暖空气及华南低空西南急流的影响，往往造成雨量大，持续时间长，形成汛期，称为前汛期[1,11]。

我国气象上规定，24 h降水量有50 mm或以上的雨，定义为“暴雨”[12]。根据降水强度分为三级。其范围在50～99.9 mm，则定义为“暴雨”；100～199.9 mm，定义为“大暴雨”；200 mm以上，定义为“特大暴雨”。由于该研究区在1951—2018年的前汛期期间的24 h降水量无大于200 mm，因此本文仅研究暴雨和大暴雨两个等级的情况。

1.2.3 降水变率 降水变率是指降水量的年(或季、月)际变化，是降水绝对变率(又称降水距平)。它是指某地实际降水量与同期多年平均降水量之差与多年平均降水量的百分比，具体计算公式如下[13]：

(1)

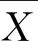
1.2.4 Morlet小波分析方法 小波分析是以Fourier变换为基础，运用三角函数来表示信号和解释时域成分的一种研究方法[14]，通过小波函数变换判断某段时间的周期振荡特点。基本小波为平方可积函数t，t∈L2(R)，对t伸缩和平移得一簇函数，即连续小波t，再计算小波变换系数和小波方差，本文采用的Morlet小波为：

(2)

式中:kφ=10，分析小波为:

(3)

式中:c>0,b∈R；c为尺度参数；d为平移参数。

(4)

Morlet小波系数的实部表示不同特征时间尺度信号在不同时间上的分布和位相，正的小波系数反映出分析对象在该时间段为偏多期，反之为偏少期，零值则为突变点。

1.2.5 Man-Kendall趋势检验与突变 本文采用Man-Kendall (M-K检验)是非参数秩次统计检验法，用于研究降水变化趋势与突变分析。M-K检验应用于水文和气象要素分析[15]，在Man-Kendall趋势检验中，n个独立的、随机变量同分布的样本为时间序列数据Xi(i=1,2,3,…,n)；假设是双边检验。对于所有的i，j≤n，且i≠j，xk和xj的分布是不相同的。定义检验统计量S：

(5)

(6)

式中:取值如下:

(7)

当M-K统计量公式如下：

(8)

此外，M-K法还可研究突变检验：把具有n个样本量的时间序列为Xi(i=1,2,3,…,n)，确定统计量：

(9)

式中:j=1,2,…，i；k=1,2,…，n。在假设时间序列随机独立时:

E[Sk]=k(k-1)/4 1≤k≤n

(10)

(11)

将标准化：

(12)

UBk=-UFk,i′=n+1-I,i′=12,L,n,…,

(13)

最后，将UBk和UFk的值分别组成曲线，当UBk或UFk的值大于0，则表明降水量为上升的特点，反之则相反；如果和两条曲线出现交点，且交点在а值临界线之间，那么交点为突变开始。UBk大于临界值，则变化明显。

1.2.6 皮尔逊三型频率曲线 根据皮尔逊三型频率曲线对于概率事件预测的优越性，本文用于分析韶关市前汛期不同等级的暴雨数据，计算其重现期，对当地的暴雨频次进行预测，为当地防洪防旱工作提供数据支持。

皮尔逊三型频率曲线的绘制要求求出指定的频率P所对应的随机变量xp，也就是对密度曲线进行积分[16]，即：

(14)

求出等于及大于xp的累计频率p值。实际操作还可通过变量转换，则：

(15)

式中:x,Cv,Cs为3个统计参数,分别代表均值、离差系数和偏态系数。频率计算就是如何从样本资料中估算3个参数值,比如矩法公式、极大似然法、概率权重矩法等,但图解适线(即“三点法”)来确定参数较简便。

频率曲线绘制后，可在频率曲线上求频率P的设计值xp。由于“频率”比较抽象，可用水文学的“重现期”表示。两者的关系式为：当频率p<50%，重现期T为：

T=1/P

(16)

当频率P>50%，重现期T为：

T=1/(1-P)

(17)

2 结果与分析

2.1 前汛期暴雨变化特征

2.1.1 前汛期暴雨变化特征 对1951—2018年韶关市前汛期的降水特征进行统计，结果表明：前汛期年降水变率极大值为2.36，出现在1957年；1963—1992年中(除了1970年、1972年、1973年、1974年、1975年的相对变率分布在0.00%～50%)，其余年份降水相对变率较稳定，均分布在0.00%～-50%；1993—2018年中，降水较多的年份有10 a，分别是1993年、1994年、1998年、2001年、2005年、2010年、2012年、2014年、2015年、2016年，降水较少的有16 a且降水变率小于35%，分别是1995年、1996年、1997年、1999年、2000年、2002年、2003年、2004年、2006年、2007年、2008年、2009年、2011年、2013年、2017年、2018年。其中，降水变率大于50%的有1954年、1957年、1962年、1993年、2010年、2015年共6 a。综上，说明68 a间，降水变率差异大，但总体在增加。

前汛期暴雨变率变化曲线与降水变率基本一致，前汛期暴雨变率最大值为2.70，出现在2015年。1951—1955年大部分年份的降水较多；降水较少的年份主要分布在1956—1992年、1997年、1999年、2001年、2002年、2007年、2008年、2011年、2014年、2017年、2018年，其中，降水变率为-100%的有1967年、1970年、1979年、1985年、1986年共5 a，即这五年的暴雨量为0 mm。而降水变率大于100%的有6 a，分别为1954年、1962年、1993年、2005年、2010年、2015年。说明90年代以后暴雨变率变化大，极端降水发生的频率高，极端事件增多的趋势一致。

前汛期暴雨对前汛期降水的平均贡献率为27%，最大暴雨贡献率为65.7%，出现在2015年。前汛期暴雨贡献率大于40%的有13 a，分别为1953年、1954年、1955年、1962年、1972年、1993年、1995年、1996年、2000年、2003年、2005年、2015年、2016年，均为前汛期暴雨贡献率高峰期。

由韶关市1951—2018年前汛期降水变率与前汛期暴雨变率和前汛期暴雨的贡献率(图1)可得，在1992年以后前汛期暴雨变率有明显的增大，而降水变率也明显加大，即近30 a极端降水事件发生几率将加大。过去68 a间，以1992年为界点，降水变率差异大，即1992年以后易出现洪涝灾害。

图1 1951-2018年韶关前汛期降水变率与前汛期暴雨

分析韶关市68 a间4—6月逐月暴雨量占前汛期雨量比例的年际变化特征(图2)，可以看出：4月累积暴雨量<5月累积暴雨量<6月累积暴雨量，但是部分年份出现差异。比如、1951年、1983年、1996—2000年、2004年、2007年中4月的暴雨量为前汛期暴雨量之首，其中1951年4月暴雨量占前汛期降水的比例高达33%；而5月暴雨量的比例为最高的年份则有1980—1982年、2010—2015年、其中2015年的比例是各年份中前汛期逐月暴雨占前汛期降水的比例的最高值、为49%；而6月暴雨量的比例为最高的年份有1952—1968年、1990—1995年、2005年、2009年、2016—2018年，其中1995年的比例占46%为最高。综上，4月份的累积暴雨量占前汛期雨量的比例最小，5月、6月份的累积暴雨量占前汛期雨量的比例较大，但是部分年份的前汛期逐月暴雨量变化差异大，在气象观测中应加强关注，为韶关市防洪抗旱灾做好预测。

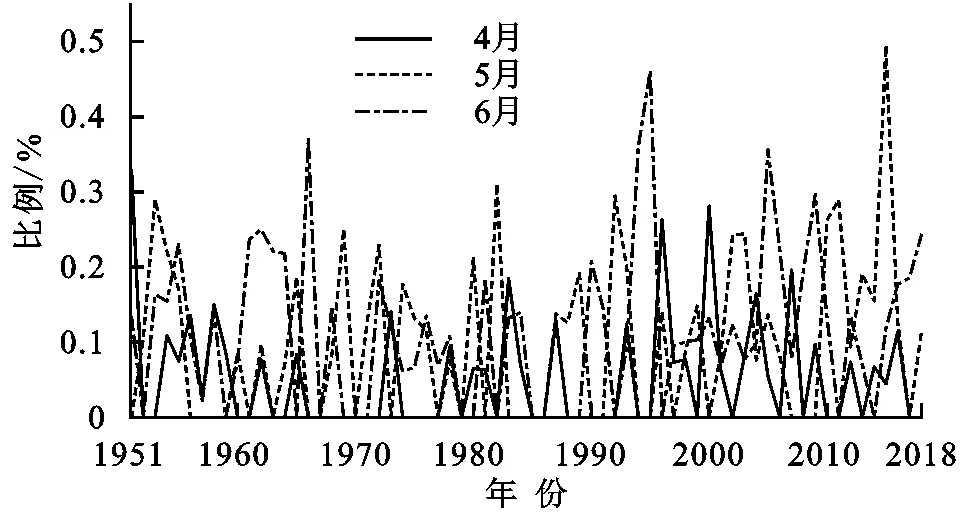
图2 不同年份4-6月逐月暴雨占前汛期雨量比例

2.1.2 前汛期不同等级暴雨多时间尺度变化特征 1951—2018年韶关市出现暴雨频次共为341 d，全年平均暴雨频次为5 d，年极大值为12 d，出现在2015年、2016年，而有个别年份无暴雨出现(1986年)；68 a间韶关前汛期出现暴雨频次198 d，前汛期年平均暴雨频次为3 d，极大值为9 d，出现在2015年，有5个年份前汛期未出现暴雨，分别是1967年、1970年、1985年、1986年；另外68 a间前汛期暴雨频次约占全年暴雨频次的58.06%。由此可见，前汛期暴雨对全年暴雨有较大影响，导致韶关市发生旱涝灾害的几率变大。

分析全年暴雨频次和前汛期暴雨频次变化特征发现(图3)，二者变化曲线基本一致，在过去的68 a间，前汛期暴雨频次总体呈波动上升的趋势，气候倾向率为0.02次/a，上升趋势明显。

图3 全年暴雨频次和前汛期暴雨频次变化

从暴雨日数的年际变化来看(图4)，1951—2018年的暴雨雨日共175 d，年平均暴雨雨日为2.6 d，其中1951年、2005年、2016年最多，为7 d，1967年、1969年、1970年、1979年、1985年、1986年、1990年最少为0 d，暴雨日数的变化幅度较大；出现大暴雨雨日共23 d，年均0.34 d，其中2015年、1993年最多，为3 d，出现大暴雨日数为0 d的有50 a，且大暴雨日数的年际变化趋势为从无到剧烈增加，说明韶关市68 a来发生大暴雨事件的变率较大，对韶关市同期的农业、水利和防洪抗灾的影响较大。综上，68 a间前汛期发生暴雨的频次最多且对同期韶关市暴雨贡献较大，大暴雨发生频次虽少，但因其降水量大，一旦发生易增加韶关市旱涝事件。

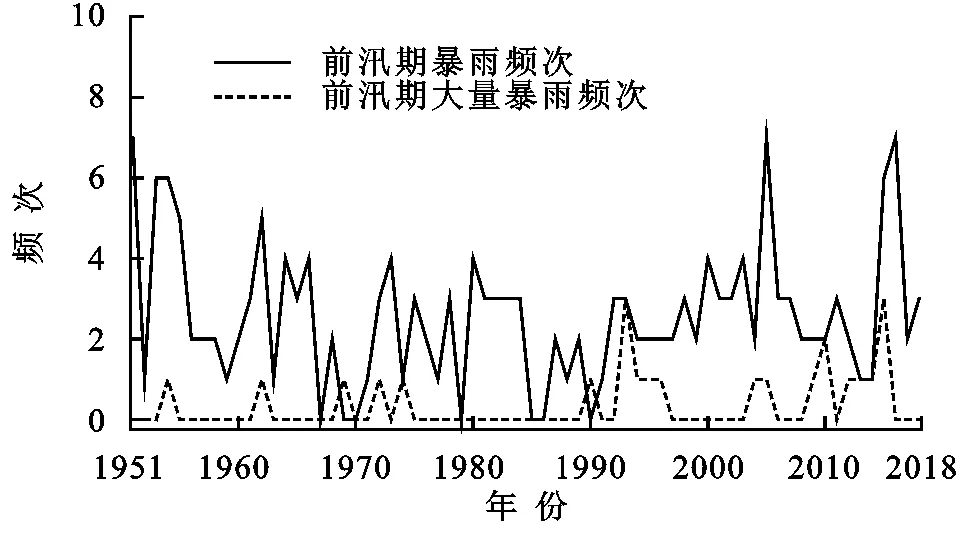
图4 前汛期暴雨、大暴雨频次年际变化

2.1.3 韶关市前汛期不同等级暴雨量的Man-Kendall趋势检验与突变分析 通过Man-Kendall法对68 a来韶关市的前汛期不同等级的暴雨量进行趋势检验与突变分析，结果见表1和图5所示。68 a来韶关市大暴雨等级的降水量呈明显上升趋势，通过了显著性检验(|Z|值大于1.28)，韶关市1951—2018年来前汛期的大暴雨等级的雨量上升趋势显著。而暴雨等级的降雨量的变化趋势，未通过显著性检验(|Z|值小于1.28)，韶关市前汛期暴雨下降趋势不显著。

由图6A可知，前汛期暴雨从1951—1998年、2007—2016年有明显的上升趋势，并且通过了0.05显著性检验(U0.05=1.96)。在1952—1955年中，UF(k)大于0.01显著水平(U0.01=2.56)，这表明在1952—1955年中韶关市的暴雨量增加的趋势十分显著。根据UF(k)和UB(k)曲线交点的位置，确定韶关市前汛期暴雨量的变化存在4个突变点，分别为1953年(上升趋势)；1957年(下降趋势)；2006年(下降趋势向上升趋势的转变)以及2015年(平稳趋势向下降趋势的转变)。

表1 韶关市前汛期不同等级暴雨变化趋势的M-K检验结果

图5 前汛期暴雨、大暴雨总量年际变化

由图6B可知，大暴雨的UF曲线的变化趋势并没有通过0.05显著性检验(U0.05=1.96)。在1951年、1952年中，UF(k)大于0.01显著水平(U0.01=2.56)，所以韶关市前汛期的大暴雨在1951年、1952年间的上升趋势十分显著。在1960年、1961年、1963—2018年中、UF(k)大于0.01显著水平(U0.01=2.56)、所以韶关市前汛期的大暴雨在此期间的下降趋势十分显著。

图6 韶关市前汛期不同等级暴雨量M-K统计曲线

2.2 韶关市前汛期不同等级暴雨日数的周期性分析

由图7的前汛期不同等级68 a来暴雨日数序列的小波变换时频分布图，可知在不同等级中都存在多重时间周期尺度上的镶套复杂结构现象。

由图7A可得，前汛期暴雨明显可见存在6～9 a短期震荡周期、12～18 a的中期震荡周期、22 a的长期震荡周期。为了得到更加准确的降水量周期特征，计算前汛期不同等级的暴雨日数的小波变换方差，得出其主要周期(图8)。由图8A可得，暴雨频次序列存在22 a的主振荡周期，其中15 a，8 a，6 a的振荡周期也明显可见。从图7A的变化规律看，1951—1990年韶关前汛期暴雨正处在6 a短期震荡的少降水期，2005—2018年韶关前汛期暴雨正处在8 a短期震荡的少降水期；68 a来存在着15 a的震荡期，期间经历了多→少→少→多→少→多→少→多→少→多十个循环交替；22 a的震荡周期是震荡信号最强的周期，且存在着少→多→少→多→少→多→少7个循环交替，其中在2018年的震荡周期等值线未闭合，则2018年以后在22 a周期上降水量将处于偏少降水时期。

图7 韶关市前汛期不同等级暴雨日数变化的小波变换实部的时频分布

由图7B可得，前汛期大暴雨日数明显可见存在4～8 a短期震荡周期、15～18 a的中期震荡周期、27～28 a的长期震荡周期。为了得到更加准确的降水量周期特征，图8通过计算前汛期不同等级的大暴雨日数的小波变换方差，可直接给出其主要周期。由图8B可得大暴雨日数序列存在27 a的主振荡周期，其中4 a，8 a，15 a的振荡周期也明显可见。从图7B的变化规律看，1951—1975年韶关前汛期大暴雨正处在4 a短期震荡的少降水期，2000—2016年韶关前汛期大暴雨正处在8 a短期震荡的少降水期；1990年来存在着15 a的震荡期，期间经历了多→少→多→少→多→少→多→少→多9个循环交替；27 a的震荡周期是震荡信号最强的周期，且存在着少→多→少→多→少5个循环交替，其中在2018年的震荡周期等值线仍未闭合，则2018年以后在27 a周期上降水量处于偏少降水时期。

1951—2018年韶关市的前汛期不同等级年际暴雨日数受多重震荡周期性规律控制，明显存在6 a和8 a的短期震荡周期、15 a的中期震荡周期以及22 a和27 a的长期震荡周期。其中从剧烈的震荡周期来看，27 a的长期震荡周期是韶关市前汛期暴雨日数的主要震荡周期，同时，6 a，8 a的短期震荡周期以及15 a的中期震荡周期都对68 a来韶关市年际前汛期暴雨日数的周期有一定的影响。

2.3 韶关市前汛期不同等级暴雨频次的重现期

采用皮尔逊三型频率曲线对韶关市前汛期不同等级暴雨频次的概率分布进行拟合，结合暴雨的分布特征和管理，为韶关市设计暴雨的雨型提供参考。对图9进行分析，在不考虑个别异常点的前提下，可得出以下结论：

前汛期暴雨频次：由图9A可得在Cs=2Cv时的理论分布对经验频率小于50%的拟合效果最好。当Cv=0.67时，出现暴雨频次为7的频率为2%～5%，重现期为20～50 a，即二十至五十年一遇，属于小概率事件；暴雨频次为6的频率为5%～10%，重现期为10～20 a；暴雨频次为5的频率为10%，重现期为10 a；暴雨频次为4的频率为10%～20%，重现期为5～10 a；暴雨频次为3的频率为20%～48%，重现期为2～5 a；暴雨频次为2的频率为50%～75%，重现期为2～4 a；暴雨频次为1的频率为75%～90%，重现期为4～10 a；暴雨频次为0的频率为90%～99%，重现期为10～100年。综上，年暴雨频次较多的属于小概率事件，如7次、6次、5次；年暴雨频次较少的发生概率较大，如3次、2次、1次和0次。

图8 韶关市前汛期不同等级暴雨日数小波方差

前汛期大暴雨频次：由图9B可得在Cs=Cv时的理论分布对经验频率小于50%的拟合效果最好。当Cv=1.95时，出现大暴雨频次为3的频率为2%～5%，重现期为20～50 a，即二十至五十年一遇，属于小概率事件；大暴雨频次为2的频率为5%，重现期为20 a；大暴雨频次为1的频率为5%～30%，重现期为3.3～20 a；暴雨频次为0的频率为30%～99%，重现期为30～100年。综上，年大暴雨频次较多的属于小概率事件，如2次；年暴雨频次较少的发生概率较大，如1次和0次。

综上，年暴雨频次较多的属于小概率事件，但对于研究暴雨洪水问题有重要意义；年暴雨频次较少的发生概率较大，对于水库兴利调节和研究枯水问题有较大意义。

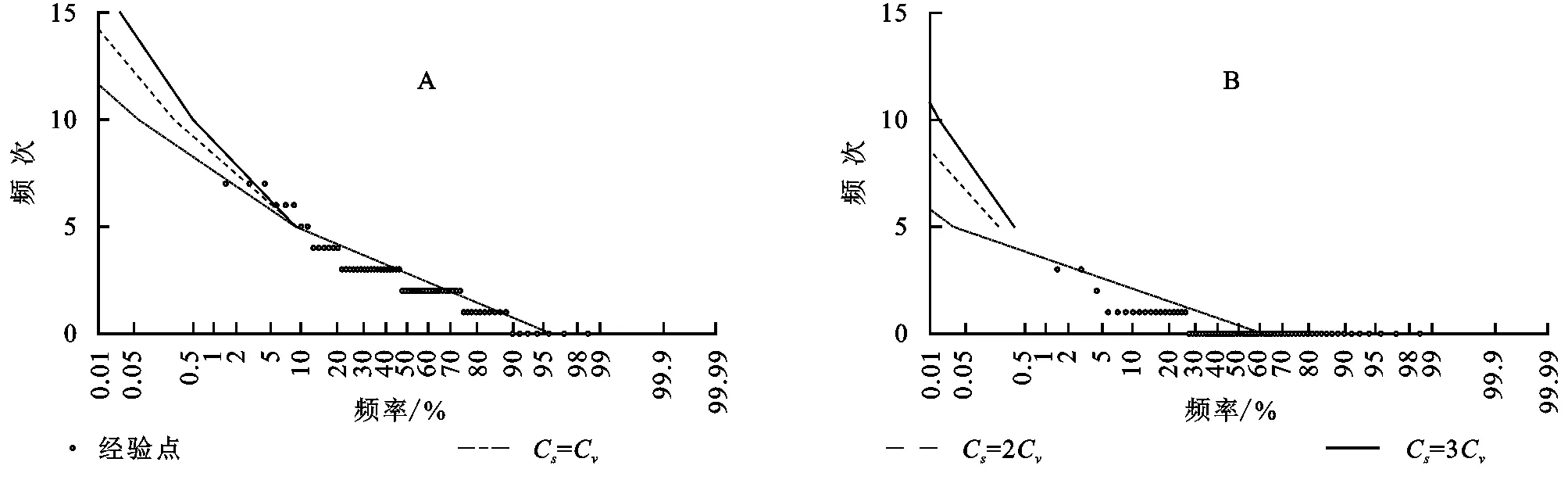
图9 韶关市前汛期不同等级暴雨频次累积频率曲线

3 结 论

(1) 前汛期暴雨对前汛期降水贡献大，平均贡献率为27%，暴雨的多少与前汛期降水呈正比关系。前汛期降水量呈明显的增加趋势，但降水变率差异大。而前汛期暴雨气候倾向率为0.02次/年，上升趋势明显。

(2) 暴雨的突变现象明显，大暴雨的上升或下降趋势显著。暴雨的UF曲线增加和下降趋势通过了0.05显著性检验(U0.05=1.95)，且有1953年、1957年、2006年、2015年4个突变点；大暴雨的UF曲线的大于置信水平，其UF曲线的变化趋势并没有通过0.05显著性检验。

(3) 68 a来韶关市的前汛期不同等级暴雨日数受多重震荡周期性规律控制，27 a，22 a的长期震荡周期是韶关市前汛期暴雨等级和大暴雨等级的暴雨日数的主要震荡周期。同时，4 a，6 a，8 a的短期震荡周期以及15 a的中期震荡周期都对68 a来韶关市年际前汛期暴雨日数的周期有一定的影响；暴雨日数的主要震荡周期是6 a，8 a，15 a，22 a，大暴雨日数为4 a，8 a，15 a，27 a。

(4) 年暴雨频次较多(7次、6次、5次)的属于小概率事件、频次较少(3次、2次、1次和0次)的发生概率较大；年大暴雨频次较多(2次)的属于小概率事件、频次较少(1次和0次)的发生概率较大。