基于遥感的科尔沁沙地蒸散发时空动态
2021-04-27张圣微高文龙杜银龙
张 鹏, 张圣微, 徐 冉, 高 露, 高文龙, 杜银龙
(1.内蒙古农业大学 水利与土木建筑工程学院, 呼和浩特 010018;2.内蒙古自治区水资源保护与利用重点实验室, 呼和浩特 010018; 3.内蒙古自治区农牧业大数据研究与应用重点实验室, 呼和浩特 010018; 4.内蒙古自治区鄂尔多斯水文勘测局, 内蒙古 鄂尔多斯 017020)
蒸散发作为连接地表能量平衡与水量平衡的关键纽带,又是联系生态环境与水文循环的重要因素[1]。蒸散发会消耗全球地表约60%的降水量,并以水汽的形式返回到空气中[2],干旱、半干旱地区(科尔沁沙地)占据我国国土面积50%以上,这部分地区降水较少,年降水量均在500 mm以下,而降水量要远低于潜在蒸散量[3],因此,想要深入了解区域生态环境问题、水循环与水文过程,准确的蒸散发是必不可少的,同时为地区水资源开发利用,荒漠化防治提供科学依据。
传统的ET测量技术(涡度相关、闪烁仪、波文比等)适用于均匀覆盖下垫面的单点ET计算,对于区域来讲,由于下垫面情况比较复杂,遥感方法被认为是计算区域ET唯一可行的方法[4]。经过数十年的发展,遥感估算蒸散发模型在理论与应用中取得了不少的成果,遥感模型在理论建设与遥感数据种类有较大的发展,其中主要的理论方法有:温度—植被指数特征空间法[5]、将遥感数据与传统方法相结合的遥感模型[6-7]、陆面过程与数据同化[8]、地表能量平衡模型等[9-10],应用较多的遥感数据有:Landsat系列数据、MODIS数据、AVHRR数据以及高分数据等。
到目前为止,应用最广泛的地表能量余项法是Bastiaanssen等人提出的地表能量平衡算法(SEBAL)[11-13]。它利用遥感的地表温度、地表发射率、NDVI和较少的地面气象观测数据(即日照时数和风速)来估计区域蒸散发。与其他使用遥感数据估算地表蒸散量模型相比,SEBAL模型具有以下优点[14]:(1) 避免了收集大量地面辅助数据;(2) 可以在每个区域进行内部定标过程来估算感热通量;(3) 基于Monin-Obukhov相似理论的内部迭代计算,避免了气温空间插值带来的不确定性。因此,SEBAL模型已被许多国家和地区成功地应用于地表热通量和ET的估算,并且经过多年的发展许多学者在不同方面对SEBAL模型进行了优化,ALLEN等人[15]在SEBAL模型的基础上加入了坡度与坡向函数,更加全面的考虑到高程的变化,进而开发出METRIC (Mapping EvapoTranspiration at high Resolution with Internalized Calibration)模型,因此METRIC模型在估算山地蒸散发中有着较高的精度;TANG等人[16]通过建立广义解析模型分析了感兴趣区以及遥感数据像元大小对于SEBAI模型结果的影响;之后TANG等[17]人通过对比SEBAL模型与Ts-Ⅵ三角模型(surface temperature-vegetation index triangle models)发现SEBAL模型能更好地估计感热通量和潜热通量。
近年来,表面通量建模涌现出许多新的思路和方法,其中引入非平衡热力学系统中最大熵增理论(maximum Entropy Production,MEP)就是其中之一。最大熵原理(maxEnt)和贝叶斯概率论是最大熵增理论的基础,由Wang和Bras经过系统的数学推导、理论分析和多次测试而发展起来的一种新型蒸散模型[18-19]。MEP模型与传统蒸散模型有较大的差异:(1) MEP模型是基于非平衡热力学理论,结合能量守恒、边界湍流等物理理论以及概率论而建立的蒸散模型[20];(2) MEP模型在求解表面通量时,仅需净辐射、地表温度、表面比湿作为已知条件,不通过风速和地表粗糙度等物理量来求解;(3) MEP模型的前提条件为地表能量闭合,以能量平衡方程作为地表通量解的数学约束条件[21]。MEP模型的创建经过了严密的推理与验证,起初Wang和Bras等[22]在估算陆面蒸散发过程中将最大熵增理论和地表能量平衡原理引入其中,并证明该方法的可行性;然后Wang和Bras等[23]认为植被在发生蒸腾的过程中内部的水分是饱和的,叶面气孔是一律张开的,此时植被蒸腾作用最强,由此建立植被蒸腾模型;最后Wang和Bras[19]对MEP模型进行了完善与验证,结果表明显热通量与感热通量二者具有良好的线性关系。自从MEP的建立,MEP模型已经得到越来越多学者的关注,大部分学者使用涡度数据对MEP模型进行验证,且验证地点多数为湿润地区,对于MEP模型在干旱半干旱地区的应用较少。Huang等[24]创新性的将MEP模型与地表辐射温度遥感数据结合,估算了时空分辨率分别为3 h和1°的全球蒸散和地表热通量,并首次给出了全球洋面热通量,以及极地地区的地表热通量;XU等[25]使用MEP模型结合站点涡度数据估算了亚马逊地区的蒸散发量,并使用MEP模型评估了MODIS ET产品,发现两者之间平均值差异较小,但是在空间上表现出较为明显的差异。随着MEP模型的不断完善与发展,MEP模型在水文学方面还存在较大的应用空间。
本文首先利用Landsat8与气象数据,估算MEP模型所需参数:净辐射(Rn)、相对湿度(RH)、地表温度(Ts),其次使用MEP模型与SEBAL模型估算研究区2016年5—10月的ET,使用涡度数据以及SEBAL模型进行验证并评估MEP模型在研究区的适用性,最后结合研究区不同土地覆被类型分析不同生态类型的ET变化特征,以期揭示科尔沁沙地不同生态类型区的水热条件的分布特征,从而为区域水资源的合理利用及荒漠化治理提供理论支持。
1 研究区概况及方法
1.1 研究区概况
研究区位于内蒙古自治区通辽市科尔沁左翼后旗阿古拉镇,地处科尔沁沙地南缘,地理坐标为122°33′00″—122°41′00″E,43°18′48″—43°42′24″N,面积约55 km2。总体上研究区地形自西向东、由南向北缓慢倾斜,西高东低。境内海拔最高为232 m,最低为186 m。研究区为固定沙丘、半固定沙丘、流动沙丘相结合,坨甸相间分布,中间地带的草甸,农田和牧场镶嵌交错分布,沙丘、草甸、湖泊、农田和村庄分别占研究区总面积的54.5%,26.6%,5.2%,10.4%,3.3%。属于典型的半干旱荒漠化地区,温带半干旱大陆性季风气候,Ф20 cm蒸发皿多年平均水面蒸发量为1 400.3 mm,多年平均降水量为379.8 mm。研究区植被种类丰富,主要有差巴嘎蒿、沙蓬、少花蒺藜草、草麻黄、虫实、冷蒿、芦苇、羊草、蒲公英等。土壤类型有:砂土、壤砂土、壤土、黑钙土、栗钙土等。土壤中砂粒占80%以上,有的甚至达到100%。
沙丘、草甸试验站点分别设有高10 m的微气象观测塔,在塔的不同高度分别布设了风、温、湿梯度传感器,并布设了辐射及涡度相关系统。两个站点所安装的均为开路式涡度通量观测系统,附加了温湿度传感器用于修正涡动相关系统所测定的空气温湿度。站点的涡动相关系统架高分别为2.62 m,4.61 m,采集频率均为10 Hz。具体观测项目见表1。

表1 涡度相关塔测量项目及仪器
1.2 数据来源及处理
本文利用的遥感数据为Landsat-8/OLI影像(2016年5—10月),获取自USGS (https:∥earthexplorer.usgs.gov/)。取清晰度高、无云或云量较少的6期影像(5—9月),每月一幅,之后对影像进行几何校正、辐射定标、大气校正等预处理工作。
气象数据(气温、标准等压面的气压、露点温度)源自中国气象数据网(http:∥data.cma.cn/),使用通辽国家气象站实测数据(2016年5—10月)。其他气象数据(气温、风速、降水、土壤温度等)分别源自研究区试验站2016年(5—10月)沙丘与草甸两个观测站的实测数据。
涡度相关系统安装的理想条件是下垫面水平均一,气流稳定等,而在实际测量中,很难达到理想状态,因此涡度数据在使用前需要预处理,处理步骤主要有:异常值及野点剔除、坐标旋转修正、数据插补和求日平均等。
DEM数据为SRTM(ShuttleRadarTopographyMission)数据,经过简单裁剪拼接等处理工作后即可使用,其空间分辨率为30 m,由于空气温度随高程变化,因此需要DEM数据进行修正,数据来源于地理空间数据云(http:∥www.gscloud.cn/)。
1.3 MEP模型
Wang和Bras在估算蒸散发的过程中,引入最大熵增原理与地表能量余项法,这一方法使得估算蒸散发更加简便[19-28]。本次研究使用他们的研究成果,并给出基于最大熵增原理的蒸散发模型的推理过程和公式。
对于无植被覆盖的地表(裸地),熵增函数D(H,E,G)的计算公式如下:
(1)
式中:H是显热通量(W/m2);Is为H的热惯性参数(W·m2·K·s1/2);E是潜热通量(W/m2);Ia为E的热惯性参数(W·m2·K·s1/2);G为土壤热通量(W/m2);Ie为G的热惯性参数(W·m2·K·s1/2)。H,E和G是利用最大熵增原理,在Rn确定的前提下,运用拉格朗日乘数法极值化D(H,E,G),得到的计算公式:
Rn=E+G+H
(2)
(3)
E=B(σ)H
(4)
(5)
式中:Rn是净辐射(W/m2),计算方法见公式(14);qs为表面比湿(g/kg);Ts为地表温度(℃);σ为无量纲参数,可通过qs与Ts得出;I0为与显热通量独立的简洁表达式,在计算H的过程中需要利用二分法或牛顿迭代法,其计算精度需要提前确定并作为约束条件。
在MEP模型中认为,植被覆盖的地表为单一封闭冠层,这时G相对于H和E可忽略不计,即Is=0,冠层上的能量平衡可以表示为:RnEv+H,Ev和H的计算公式如下:
(6)
(7)
式中:Ev为植被蒸腾作用的潜热通量(W/m2),此时的Ts为叶面温度;qs为叶面的表面比湿。
1.4 MEP模型输入参数计算方法
MEP模型的优点在于输入参数少,只需要地表温度(Ts)、净辐射(Rn)以及表面比湿(qs),地表温度的计算使用Ren等[29-30]应用通用劈窗算法针对Landsat8数据开发的模型,公式如下:

(8)
式中:Ti是第10波段(Band 10:10.6~11.19 μm)的亮度温度;Tj是第11波段(Band 11:11.5~12.51 μm)的亮度温度;ε为第10波段与第11波段的比辐射率平均值;Δε为第10波段与第11波段比辐射率的差值;bk(k=0,1,…,7) 为劈窗算法的系数;bk的取值随着大气水汽含量的变化而有所差异。使用劈窗协方差表示方差比法(Split Window Covariance-Variance Ratio,SWCVR)可以计算大气水汽含量,计算公式如下:
W=a+bτj/τi
(9)
式中:W为大气水汽含量(g/cm2);a和b为系数从模拟数据中获得;τi和τj分别为i和j波段的大气透过率。
为了方便后续模型的计算以及数据验证,将表面比湿换算为相对湿度(RH),本文将Peng等[31]使用MODIS数据估算大气水汽含量方法移植到Landsat8数据,公式如下:
RH=e/es
(10)
(11)
(12)
式中:e为地面水汽压(hpa);es为饱和水汽压(hpa);Ta为大气温度(℃);Pa为大气压(hpa);W与qs之间有着良好的线性关系,使用通辽站的实测探空数据,得到W与qs的回归方程,如式(13):
qs=0.001(-0.682W2+6.677W-1.1123)
(13)
1.5 SEBAL模型
SEBAL模型[11-13]在世界上得到了广泛应用,在不同地区、气候类型以及不同土地覆被类型下,有大量学者对SEBAL模型进行了验证,相比其他遥感模型其精度相对较高,因此本文使用SEBAL模型进行对比验证,计算过程如下:
Rn的计算公式如式(14):
Rn=(1-α)RS↓+RL↓-RL↑-(1-ε0)RL↓
(14)
式中:Rs↓为入射短波辐射(W/m2);α为地表反照率;RL↓为入射长波辐射(W/m2);RL↑为出射长波辐射(W/m2);εo为宽波段表面热发射。
土壤热通量(G)计算公式如下:
(15)
显热通量(H)计算公式如下:
(16)
式中:ρair为空气密度(kg/m3);Cp为空气定压比热(取1 004.07 J/kg/K);Ts为地表温度或冠层的表面温度(K);Ta是2 m处的气温(K);dT为Z1与Z2两个高度之间的温差(K);rah是Z1与Z2之间空气动力学阻抗;Z1,Z2分别是指0.01 m和2 m高度处。
1.6 尺度扩展方法
遥感模型中计算出的ET是卫星过境时刻的瞬时ET,在实际应用中,往往需要的是日ET,在本次研究中通过式(17)进行日尺度扩展[29]。
(17)
式中:ET24为日蒸散量(mm);λ为水分汽化潜热指数;ETrF为卫星过境瞬时参考蒸散比(mm);Rn_24为卫星过境日的净辐射通量(W/m2);G24为全天的土壤热通量(W/m2)。
2 结果与分析
2.1 MEP模型反演结果验证
利用2016年5—10月沙丘和草甸两个观测站的涡度相关数据以及气象观测数据与MEP模型估算结果、SEBAL模型估算结果、地表参数进行对比。为了更好地评价两种模型,本文选用统计学中均方根误差(RMSE)、相对误差(MRE)与拟合系数(R2)作为评价指标,对比结果见表2与表3,图1。

表2 地表参数及MEP模型结果估算误差

表3 SEBAL模型估算误差对比
由表2与表3得到,MEP模型反演G值的均方根误差与相对误差最大分别为61.50 W/m2,34%,G的拟合系数最小为0.57;SEBAL模型反演E值的均方根误差最大为47.93 W/m2,G的相对误差最大为15%,拟合系数最低为0.32;地表参数验证结果相对较好,Rn的模拟结果误差较小,其拟合系数最高为0.98,Ts的平均相对误差最小为2%。由图1看出:SEBAL模型与MEP模型之间反演结果整体误差较小,其中MEP模型的H值偏高,G的误差相对较小,个别日期的E值有着较大的差异。
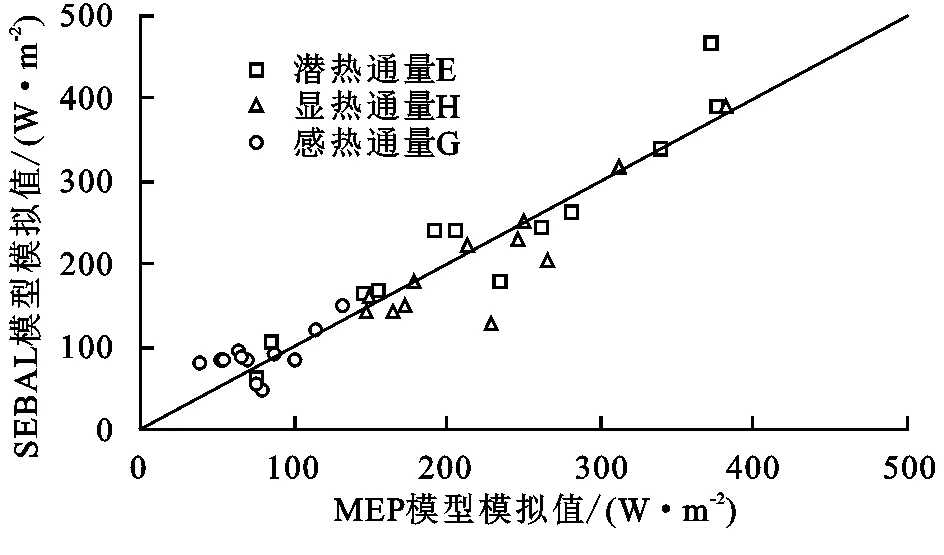
图1 MEP模型与SEBAL模型对比验证结果
利用沙丘和草甸观测数据,通过MEP模型分别反演了两点的日ET,使用实测ET数据、遥感估算的ET数据以及Penmam-Monteith模拟ET之间进行对比,对比结果见图2。

注:图中ET模拟为Penmam-Monteith模拟的ET值。
从图中看出MEP模型估算ET和实测ET变化趋势基本一致,个别日期有所差异,遥感估算ET与实测ET以遥感反演ET值与观测ET以及Penmam-Monteith模拟ET之间误差较小,结果表明MEP模型能在不同的土地覆被类型模拟出精度较高的ET值。研究区ET总体波动较为平缓,表现为5—6月呈上升趋势,7—8月相对较高,9—10月处于下降趋势。沙丘的ET明显低于草甸,随着降水量的变化,沙丘的ET波动较为剧烈。降水对ET有着较大的影响,当有降雨事件发生的日期ET会随之降低,出现一个波谷,降雨事件结束之后ET会有明显升高,出现一个波峰。总体来说:在不同土地覆被类型下,MEP模型可以估算出相对精确的ET以及较为合理的变化趋势。
2.2 MEP和SEBAL模拟ET的时空分布特征
本文通过MEP模型与SEBAL模型分别反演出研究区瞬时潜热通量,通过日ET尺度扩展方法的到日ET值,日ET时空分布见附图13,附图14。
研究区日ET最大可以达到7 mm以上,主要集中在湖泊,湖泊相对较为稳定,日ET值在4~7 mm;农田与草甸由于植被与农作物的影响日ET变化较为明显,尤其在6月、7月、8月,个别区域会有最大值出现,日ET保持在3~7 mm;沙丘日ET一直处于较低水平,保持在1~3 mm。
SEBAL模型与MEP模型得到的ET空间分布图在5—7月差异较小,8—10月差异较大,二者差异较大的区域在半固定沙丘,误差在0.5~1 mm;农田与草甸差异较小,误差在0.2~0.6 mm。主要原因有:(1) MEP模型以能量闭合为边界条件,而SEBAL模型会出现能量不闭合的情况,(2) 输入参数不同,MEP模型所需参数少,只需要3个地表参数,而SEBAL模型输入参数多,参数的不同引起结果差异,(3) 对于植被处理方法的不同:对于植被覆盖的地表MEP模型认为土壤热通量为零,直接计算显热通量,而SEBAL模型通过选取冷热点的方式估算显热通量,5—7月研究区处于春季,植被较少,8—10月研究区处于夏季植被生长茂盛,因此导致8—10月差异较大。
为进一步分析MEP模型与SEBAL模型的差异以及ET时空变化,按照不同土地覆被类型对ET时空分布图的ET平均值进行统计,得到各类土地覆被类型ET平均值变化曲线,见图3。

图3 2016年生长季不同土地覆被类型平均ET统计对比
随着时间的变化不同土地覆被类型下的ET值波动情况有所差异,但是整体呈现先增长后降低的变化趋势。5月所有土地覆被类型ET值均保持在较低水平,ET在2.5~4 mm;6月—8月大部分区域的ET值均有较为明显的升高,而沙丘地由于水分补给不充足反而降低;在9—10月ET呈现明显的下降趋势,10月除湖泊仍保持在相对较高的水平,其他区域ET值较低,ET空间分布情况与5月相似。湖泊、草甸、农田整体呈较高水平,受月份影响较为明显;沙丘波动较为明显,受月份影响相对较小,沙丘类型不同,ET分布有较大差异,其中固定沙丘和半固定沙丘相似,而流动沙丘ET处于较低水平,尤其在6—8月差异较为明显;村庄受人类活动影响较大,ET值分布相对较为集中并处于较低水平。
影响研究区ET时空分布的主要因素有:土壤类型不同,草甸地主要为黑钙土、栗钙土,沙丘地以砂土、壤砂土、壤土为主要的土壤类型,不同土壤类型下地表反照率有所差异,对太阳辐射的吸收也有差别[32],导致ET的不同;植被类型不同,随着生长季的到来植被的蒸腾作用所占蒸散发总量的比重越来越大,不同植被类型蒸腾作用有着较大差异,导致ET的不同[33];土壤含水量以及供水条件不同,农田与草甸地的土壤含水量较高且水分供应充足,而沙丘地土壤含水量低,地下水埋深较深,除天然降水外,没有其他水源供给,因此沙丘ET要低于农田与草甸[34]。
3 结 论
(1) 各地表参数以及ET估算值与地表观测数据一致性较高,MEP模型与SEBAL模型对于日蒸散量的估算较为准确与误差较小,表明两个模型结合遥感数据均可为研究区提供合理的地表参数与ET模拟值。
(2) 通过对两个模型的对比得出:两个模型对于ET的估算较为一致,MEP模型估算的ET值要略低于SEBAL模型的估算值,个别日期两个模型在沙丘地表现出较为明显的差异,误差在1.5 mm左右。导致差异的原因主要是由于边界条件、输入参数的不同以及对于植被处理方法的不同所导致。
(3) 研究区ET时空变化规律为:时间上ET呈现出5月较低,6—7月升高,8月达到最大,9月—10月呈下降趋势,且降低幅度较大的变化规律;空间分布表现为:湖泊一直保持较高态势,农田与草甸次之,沙丘最低的空间分布情况。影响ET主要因素有:土地类型以及土壤含水量不同、植被类型以及植被数量不同、人类活动。
