关于丢番图方程x3-1=1261y2

吴小英

(四川师范大学 数学科学学院,四川 成都 610068)

0 引言

设整数D>2,且无平方因子.丢番图方程

x3±1=Dy2

(1)

是一类重要的丢番图方程,对这类方程整数解的研究已产出大量的文献.柯召、孙琦在文[1,2]中证明了当且仅当D不含6k+1型素数时,方程(1)无非平凡解.但当D含6k+1型素因数时,方程的解的情况比较复杂，求解过程亦较为困难.2003年，罗明证明了x3+1=7y2仅有整数解(x,y)=(-1,0)，(3,±2)[3].2009年，瞿云云等人证明了x3+1=119y2仅有整数解(x,y)=(-1,0)[4].本文利用Pell方程的解所给出的递归数列的性质与同余式证明了丢番图方程x3-1=1261y2仅有整数解(x,y)=(1,0).

1 引理

引理1[5]若D是一个非平方的正整数,则Pell方程

x2-Dy2=1,x,y∈N+，

(2)

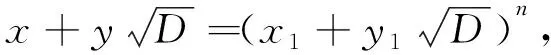
引理2[6]方程4x4-3y2=1仅有整数解(x,y)=(±1,±1).

引理3[6]丢番图方程x2-3y4=1仅有整数解(x,y)=(±2,±1),(±7,±2),(±1,0).

引理4[6]丢番图方程x4-3y2=1仅有整数解(x,y)=(±1,0).

2 主要结果

定理1 丢番图方程

x3-1=1261y2

(3)

仅有正整数解(x,y)=(1,0).

定理1的证明设(x,y)是(3)的解.因为gcd(x+1,x2-x+1)=1或3,故分以下8种情况进行讨论：

(I)x-1=a2，x2+x+1=1261b2,y=ab;

(II)x-1=13a2，x2+x+1=97b2,y=ab;

(III)x-1=97a2，x2+x+1=13b2,y=ab;

(IV)x-1=1261a2，x2+x+1=b2,y=ab;

(V)x-1=3a2，x2+x+1=3783b2,y=3ab;

(VI)x-1=39a2，x2+x+1=291b2,y=3ab;

(VII)x-1=291a2，x2+x+1=39b2,y=3ab;

(VIII)x-1=3783a2，x2+x+1=3b2,y=3ab，

这里，a≥0,b>0,gcd(a,b)=1.

情形(I)将第二式两边模13,得x2+x+1≡0(mod 13),解之得x≡3,9(mod 13),代入第一个方程，有a2=x-1≡2,8(mod 13).但模13的Legendre符号

故在该情形时方程(3)无整数解.

情形(II)将第一式的两边模13,得x≡1(mod 13).代入第二个方程，得3≡x2+x+1=97b2≡6b2(mod 13).因而， 2b2≡1(mod 13),解之得,b2≡7(mod 13). 但模13的Legendre符号

故在该情形时方程(3)无整数解.

情形(III)将第二式两边模8,得x2+x+1≡5(mod 8),解之得x≡3,4(mod 8),代入第一个方程，有2,3≡x-1=97a2≡a2(mod 8).这是不可能的.

故在该情形时方程(3)无整数解.

情形(IV)由第二个方程,得x=0，-1.但x=0，-1，均不满足第一个方程,故在该情形时方程(3)无整数解.

情形(V)将第二式两边模13,得x2+x+1≡0(mod 13),解之得x≡3,9(mod 13),代入第一个方程，有3a2=x-1≡2,8(mod 13)，解之得,b2≡5,7(mod 13).但模13的Legendre符号

故在该情形时方程(3)无整数解.

情形(VI)将第一式的两边模13,得x≡1(mod 13)，代入第二个方程，得3≡x2+x+1=291b2≡5b2(mod 13).因而，2b2≡1(mod 13),解之得,b2≡11(mod 13). 但模13的Legendre符号

故在该情形时方程(3)无整数解.

情形(VII)将第一式的两边模97,得x≡1(mod 97).代入第二个方程，得3≡x2+x+1=39b2(mod 97).因而，13b2≡1(mod 97).但模97的Legendre符号

故在该情形时方程(3)无整数解.

情形(VIII)将第一式代入第二式,得(2b)2-3(2522a2+1)2=1.由引理1知方程(2b)2-3×(2522a2+1)2=1的全部整数解可表示为

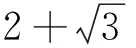
2522a2=yn-1,n∈Z.

(4)

容易验证以下的等式成立：

xn±1=2xn±3yn,yn±1=±xn+2yn；

(5)

(6)

xn+2=4xn+1-xn,x0=1,x1=2；

(7)

yn+2=4yn+1-yn,y0=0,y1=1.

(8)

对递归序列(8)取模13,得周期为12的剩余类序列，0，1，4，2，4，1，0，12，9，11，9，12.因而当且仅当n≡1,5(mod 12)时,yn≡1(mod 13).

因为n≡1,5(mod 12)，故n≡1(mod 4).令n≡4m+1，则由式(6),得

2522a2=yn-1=y4m+1-1=y4m-1+1=x4m+2y4m-1=

即 1261a2=x2m+1y2m.

(9)

又gcd(x2m+1,y2m)=2,故(9)可分解成

x2m+1=2c2,y2m=2522d2,a=2cd；

(10)

x2m+1=2522c2,y2m=2d2,a=2cd；

(11)

x2m+1=26c2,y2m=194d2,a=2cd;

(12)

x2m+1=194c2,y2m=26d2,a=2cd,

(13)

这里，c>0,d≥0,gcd(c,d)=1.

将(11)的第二式代入y2m=2xmym,得xmym=d2.故有

xm=u2,ym=v2,d=uv.

(14)

这里，u>0,v≥0,gcd(u,v)=1.

将(12)的第二式代入y2m=2xmym,得xmym=97d2.故有

xm=u2,ym=97v2,d=uv；

(15)

xm=97u2,ym=v2,d=uv.

(16)

这里，u>0,v≥0,gcd(u,v)=1.

类似于(14)，(15)无满足条件的整数解.

类似于(12)，(13)无满足条件的整数解.

综上所述, 丢番图方程x3-1=1261y2仅有整数解(x,y)=(1,0).