破解直角坐标系下三重积分的计算方法——大学生思维能力培养案例剖析

王俊梅，辛海军

(1.吕梁学院 数学系，山西 离石 033001；2.离石区教育科技局，山西 离石 033000)

0 引言

直角坐标系下三重积分的计算是高等数学中的难点.直角坐标系下三重积分的计算方法有“先单后重”(又称“穿针法”)和“先重后单”(又称“切片法”)[1，2].所谓“先单后重”，就是将三重积分的计算转化为：先计算一个定积分，再计算一个二重积分.同理，“先重后单”就是先计算一个二重积分，再计算一个定积分来完成三重积分的计算.对于学生而言，在定积分和二重积分的计算已经掌握的前提下，不管是“先单后重”还是“先重后单”，如何确定定积分的积分区间和二重积分的积分域都是难点.大多数学生即便能够机械套用这些方法，也不清楚为什么可以这么处理.如何选择“先重后单”和“先单后重”，“先重后单”和“先单后重”的本质是什么？引导学生提出问题、分析问题、解决问题的过程是学生数学思维能力、学习能力培养与提高的过程.

1 破解直角坐标系下三重积分的计算

1.1 “转化”——三重积分计算的数学思想

“转化”是重要的数学思想，它的核心是化未知为已知、化难为易、化繁为简、化曲为直等. 二重积分的计算是转化为两个定积分即二次积分的计算实现的.在简单回顾二重积分的计算思想之后，引导学生提出猜想：三重积分的计算是否可以转化为定积分和二重积分的计算？

将三重积分转化为定积分和二重积分有两种情况：“先单后重”和“先重后单”.这两种情况的区别在于：先计算定积分还是先计算二重积分.但是，不管是“先单后重”还是“先重后单”都会遇到同一个问题：如何确定定积分的积分区间和二重积分的积分域.以下为方便表述，必要时将一二三重积分的积分范围统称为“积分限”.

1.2 “数形结合”探寻三重积分计算方法的本质

运用“数形结合”思想，从积分表达式入手，借助积分域的图形，由三重积分探寻定积分和二重积分的积分限.首先，提醒学生明确三点：1.积分限是几何区域，它是积分变量的取值范围，因此它“限制”的对象仅是“积分变量”；2.由于积分限“限制”的对象是“积分变量”，所以有几个积分变量就应该有几维的积分限，即积分限的维数与积分变量的个数是相等的；3.因为三重积分提供的信息只有积分域Ω和积分表达式，所以新“积分限”的确定只能取决于Ω和被积表达式.然后，就可以引导学生着手研究如何由三重积分的积分域Ω和被积表达式确定新积分限.我们将重点展示和剖析如何探求定积分和二重积分的积分限.

(1)“单”限的确定

从定积分的被积表达式f(x,y,z)dz，可以看出：被积函数f(x,y,z)有三个自变量x,y,z，而积分变量却只有z.这意味着什么呢？当然是，在这个定积分中，只有z应该被看作变量，而x,y只能被看作“不变量”.将被积表达式中积分变量之外的变量称为“无关变量”.

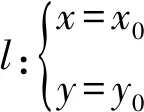
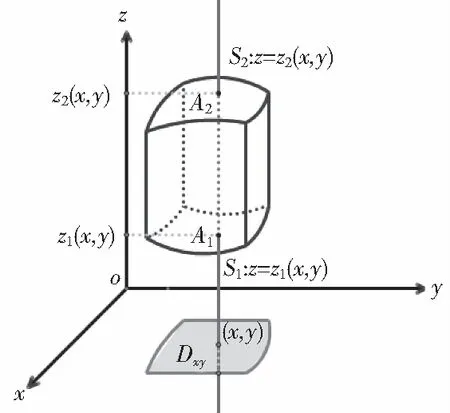
图1

(2)“重”限的确定

由二重积分的被积表达式F(x,y)dxdy，可以看出：被积函数F(x,y)有两个自变量x,y，而这两个自变量恰好也是积分变量，因此没有无关变量.没有无关变量意味着什么呢？它意味着：所求“重”限是一个不受无关变量影响，仅由Ω唯一确定的平面区域，它限定了积分变量x,y的取值范围，将其记作Dxy(见图1).显然，Dxy就是Ω上点的横纵坐标的取值区域，即Ω在xoy坐标面上的投影区域，可由Ω向xoy坐标面投影得到.

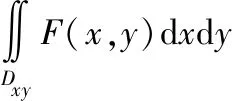
(3)“单”限和“重”限的关系

显然，平行于z轴的直线l要穿过Ω且产生两个交点，l必然穿过Dxy内部.也就是说，只有在区域Dxy内“穿针”，才可以在Ω中穿出线段A1A2，从而得到“单”限I(x,y).简言之，只有当(x,y)∈Dxy∂Dxy即(x,y)在“重”限Dxy内部时才能通过“穿针”得到“单”限I(x,y).事实上，所有“穿针”得到的线段的集合就是Ω(可能会缺失一些边界点).

下面，引导学生探寻另外一种情形.在这种情形下,为了便于观察图形,图示中选用了不同于情形1的积分域Ω,不影响研究过程和结论.

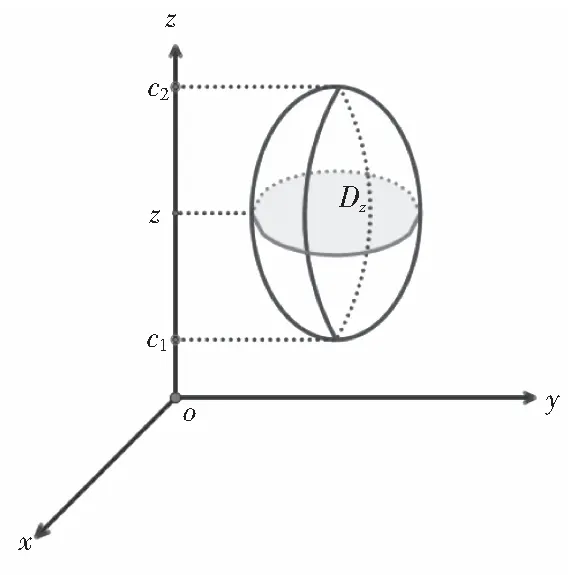
图2

(1)“重”限的确定

(2)“单”限的确定

由定积分的被积表达式G(z)dz，可以看出：被积函数G(z)有一个自变量z，而这个自变量恰好也是积分变量，所以没有无关变量.没有无关变量意味着：所求“单”限是一个不受无关变量影响，仅由Ω唯一确定的区间，它限定了积分变量z的取值范围，将其记作Iz(见图2).显然，Iz就是Ω上点的竖坐标的取值区间，即Ω在z轴上的投影区间，可由Ω向z轴投影得到.

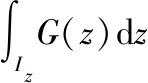
(3)“重”限和“单”限的关系

平行于xoy坐标面的平面要将Ω切出一个平面区域，必然经过Iz的内部.也就是说，只有在区间Iz的内部“切片”才可以在Ω上切出平面区域D(z)，从而得到“重”限.事实上，所有“切片”得到的平面区域的集合就是Ω(可能会缺失一些边界点).

2 在实践中总结内化、重构凝练、反思升华

2.1 总结内化

对比两种方法，学生们会发现：1.对于先积的积分，使用“穿针法”或“切片法”确定积分限.其中，只有一个积分变量时，在一维空间取值，用“穿针法”；有两个积分变量时，在二维空间取值，用“切片法”.2.对于后积的积分，都用“投影法”确定积分限.

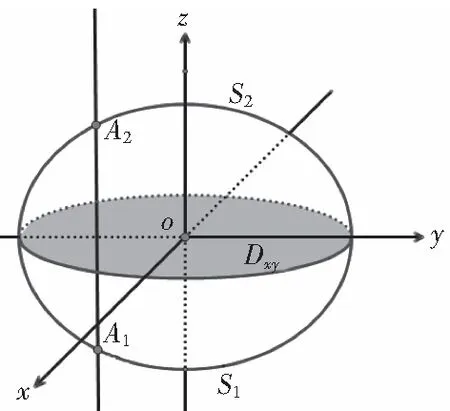
图3

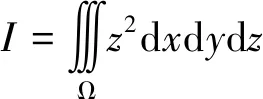
分析1：主要分析“先单后重”的定限过程

“穿针”定“单”限.用平行于z轴的直线穿过Ω，与下边界曲面S1和上边界曲面S2分别交于两点A1与A2，因此所求“单”限应为线段A1A2(见图3).

“投影”定“重”限.将Ω向xoy坐标面投影，会得到一个投影柱体，它的边界曲面是母线平行于z轴的柱面，这个柱面与xoy坐标面的交线所围成的区域就是所求“重”限Dxy(见图3).这样，学生就从几何角度，直观地看到了所求积分限.

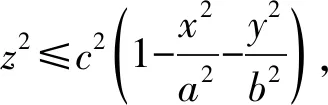
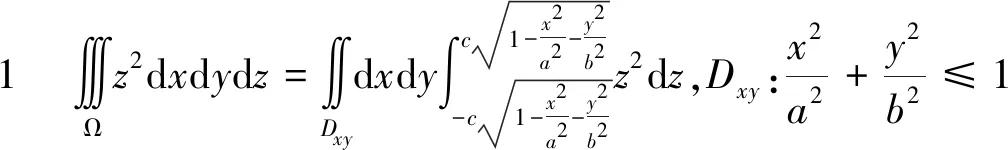
分析2：主要分析“先重后单”的定限过程

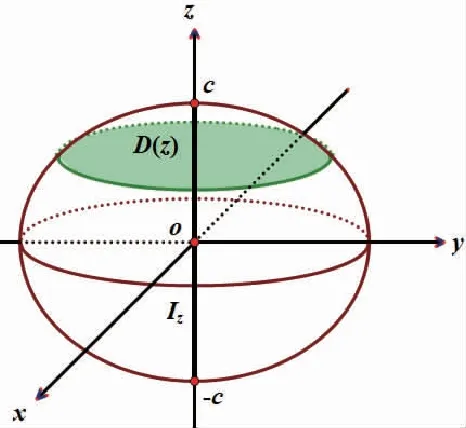
图4

“切片”定“重”限.用平行于xoy坐标面的平面切割Ω，切得平面区域D(z)(见图4).

“投影”定“单”限.将Ω向z轴投影，得到投影区间Iz(见图4).事实上，Iz也可由两个平行于xoy坐标面且与Ω均相切的平面截z轴而得.这样，学生就从几何角度，直观地看到了所求积分限.

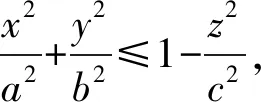
虽然两种方法都可算出三重积分，但学生很快就会发现“先重后单”计算量小很多，从而体会到：计算方法的选取非常重要.要求学生在练习过程中，认真总结两种方法的适用题型.

2.2 重构凝练

从几何和代数两个角度再次对定限方法进行总结凝练，将结论一般化.

几何角度操作时，平行于积分变量所在坐标轴(坐标面)向Ω“穿针”(“截面”)即可作出第一个积分限；将Ω投影到积分变量所在坐标面(坐标轴)便可作出第二个积分限.

代数求解时，先将积分域Ω表达式中积分变量和其余变量分离：分别置于不等号两边即可求得第一个积分限；再将上一步分离出来的积分变量在积分域Ω的表达式中置为某常数(这个常数的选取应使所求区间或区域达到最大)，便可求得第二个积分限.当边界曲面比较复杂时，常数的选取往往需要结合Ω的图形来确定.

2.3 反思升华

对破解三重积分计算方法的整个过程进行反思，将实践结果提升到理论高度.

在处理三重积分计算时，三个积分变量相互纠缠，处于一个复杂的矛盾之中.先将它们分别放在一个定积分和一个二重积分之中，降低矛盾的复杂度；然后将一个作为主要矛盾，另一个作为次要矛盾依次处理.这样，三重积分的计算就迎刃而解了(本节主要破解三重积分的计算方法).这是“道”层面的问题.

在探寻三重积分解法本质的过程中，应用“数形结合”思想，利用“形”这个有力的工具，直观地剖析了三重积分解法的本质.这充分说明了工具的重要性.这是“术”层面的问题.

3 结束语

践行“以学生为中心”理念、以知识为载体培养学生的空间想象能力、逻辑思维能力和创新思维能力是本节教学的初衷.通过引导学生提出问题、分析问题、解决问题，探寻三重积分计算方法背后的数学思想和本质，并在实践中总结内化、重构凝练、反思升华，逐步培养学生的思维能力.这样的教学对学生具有一定的挑战性.当他们面对困难、束手无策、缺乏自信时，一定要及时引导，并鼓励学生做到“战略上藐视，战术上重视”.首先，保持头脑冷静，要使学生相信，通过自己的冷静分析和不懈努力，问题的答案一定会越来越清晰.其次，充分运用工具，勇于尝试，不怕失败.鼓励学生运用已有的知识、能力、信息、技术等尝试每一个可能的想法；要让他们相信，不管成功的经验还是失败的教训，都会对自己的下一步行动有积极作用.我相信，在一次次这样具有“挑战度”的教学实践中，学生的思维能力一定会越来越强.