Kundu-Eckhaus方程的N阶达布变换和精确解

刘春萍，李 丽

(沈阳师范大学 数学与系统科学学院，辽宁 沈阳 110034)

0 引言

非线性薛定谔方程含有孤立子波解，它是解释非线性现象的重要模型之一.非线性薛定谔方程可以用来描述物理模型和物理现象，例如：玻色-爱因斯坦凝聚(Bose-Einstein condensation)、非线性光学(nonlinear optics)、等离子物理(plasma physics)、凝聚态物理、流体力学，以及描述等离子波，激光束在折射率与波幅有关的介质中传播等，它在数学和物理中应用十分广泛.在2010年，C.G.Latchio-Tiofack、Alidou Mohamadou、Timoleon C.Kofane、K.Porsezian 从可积性的角度考虑了非均匀1+1维耦合非线性薛定谔方程[1]，利用达布变换，在利用3×3 Lax对的基础上，得到了精确解.在2017年，S.Vijayalekshmi、A.Mahalingam、M.S.Mani-Rajan研究了具有更广义外势的非自治非线性薛定谔方程中光孤子的传播[2].

求解孤子方程的方法有很多，如：Hirota 双线性方法[3-4]，反散射方法[5-7]，齐次平衡法[8-9]，贝克隆变换法[10-11]，达布变换(DT)法[12-13]等.达布变换是由数学家Darboux在1882年发现的.利用达布变换求新解的步骤是：利用非线性微分方程的Lax对和常微分方程的谱理论，把非线性微分方程精确解的求解过程转化为代数过程.在知道种子解的条件下，通过代数运算求得新解.很多学者利用达布变换解决了很多问题.例如：邱德勤构造了显示的达布变换的解析表示，利用泰勒展开得到了KE方程的高阶怪波解.2016年，Ablowitz和Musslimani提出了非局域的修正Korteweg-de Vries(mKdV)方程和非局域sine-Gordon(SG)方程[14]，并证明了这些方程的可积性.2017年，Ji和Zhu 通过构造非局域mKdV方程的Darboux变换获得了一系列不同类型的精确解析解[15]，包括complexiton 解、怪波解、奇异的非局域解、扭结孤子解和反扭结孤子解.在[16]中利用离散N阶Darboux变换(DT)导出了耦合Ablowitz-Ladik方程的离散呼吸和亮孤子解.在[17]中研究了一种非标准的双极化过程，用于为PT对称耦合非局部非线性薛定谔方程(CNNLS)生成更一般的亮孤子和呼吸孤子解.在[18]中研究了具有谱问题的耦合非局部非线性薛定谔方程的Darboux变换.在[4]中提出了一种广义非局部非线性Gross-Pitaevskii(GP)方程，它可以简化为具有自诱导PT对称势的非局部GP方程.利用达布变换方法求解了具有自诱导对称势的非局域非线性薛定谔方程的亮孤子解和呼吸波孤子解[19].

在本文中，构造出KE方程的N阶达布变换，获得了N-孤子解.此外，令一些参数为0时，可得到简化的1-孤子解、2-孤子解和3-孤子解.得到了一些新的精确解，包括亮孤子解和呼吸孤子解，并显示了它们的动力学特征和弹性相互作用.

1 非局域非线性Kundu-Eckhaus方程的Darboux变换

1984年，一种非线性Kundu-Eckhaus方程被提出，形式如下：

iut+uxx+2|u|2u+4β2|u|4u-4iβ(|u|2)xu=0,β∈R.

(1)

式中下标表示偏导数，方程(1)的Lax 对形式如下：

Ψx=MΨ,Ψt=NΨ=(N2λ2+N1λ+N0)Ψ,

(2)

(3)

(4)

这里*为复共轭，u是关于空间变量x和时间变量t的函数，λ是谱参数.

构建方程(1)的达布变换，引入变换T:

(5)

(6)

(7)

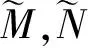
(8)

其中：

(9)

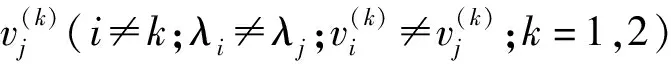
因此，给出了2×2的矩阵T，形式如下：

(10)

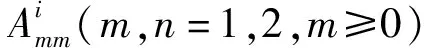
经过计算，可以得到如下形式的ΔT：

(11)

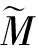
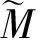
(12)

式(13)给出了方程(6)的新解和旧解的关系:

(13)

式(13)是通过方程(6)达布变换得到的.

证明设

(14)

得到的Bsl(1≤s,l≤2)是λ的2N或2N+1次多项式.

通过一些计算，λj(1≤j≤2)是Bsl(1≤s,l≤2)的根，公式(14)会有如下形式：

(Tx+TM)T*=(ΔT)C(λ).

(15)

其中

(16)

(Tx+TM)=C(λ)T.

(17)

通过比较方程(17)中λN的阶次，得到下列关系式：

(18)

(19)

(20)

(21)

易证Esl(1≤s,l≤2)是λ的N+1或N+2次多项式.通过计算，可以得到λj(1≤j≤2)是Esl(1≤s,l≤2)的根，因此，方程(21)具有下列形式:

(Tt+TN)T*=(ΔT)F(λ).

(22)

其中:

(23)

(Tt+TN)=F(λ)T.

(24)

通过比较方程(24)中的λN阶次，得到了以下方程

(25)

2 非局域非线性Kundu-Eckhaus方程的N-孤子解

为了利用达布变换求得KE方程的N-孤子解，我们首先选取一个种子解u=0,并且将这些解代入方程(2)、(3)，得到KE方程的两个基本解：

(26)

把方程(26)代入到(9)，我们可以得到

(27)

其中

为了获得方程(1)的N-孤子解，我们获得矩阵T:

(28)

(29)

根据方程(29)和克莱姆法则，得到

(30)

其中:

(31)

基于方程(9)和(27)，我们能得到

(32)

用达布变换方法得到KE方程的N-孤子解，形式如下:

(33)

(i)1-孤子解

为了获得方程(1)的1-孤子解，考虑N=1时，得到

(34)

其中:

(35)

因此，我们可以获得KE方程的1-孤子解:

(36)

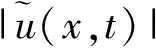
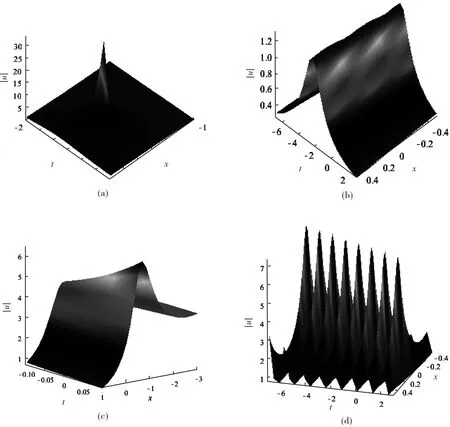
图1 方程(1)的1-孤子解

(ii)2-孤子解

为了获得方程(1)的2-孤子解，考虑N=2时，得到

(37)

其中:

(38)

因此，我们可以获得KE方程的2-孤子解:

(39)

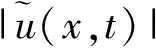
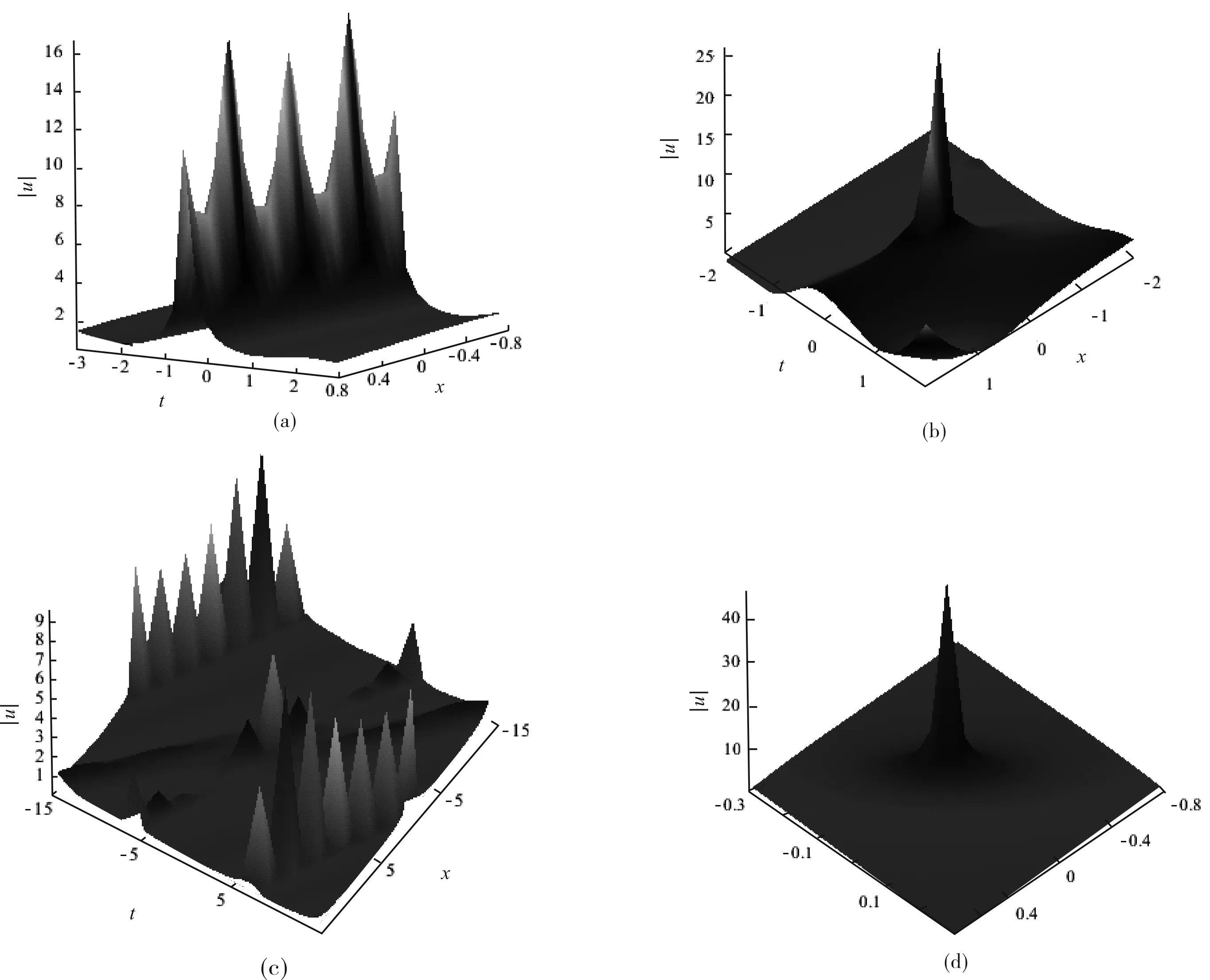
图2 方程(1)的2-孤子解

(iii)3-孤子解

为了获得方程(1)的3-孤子解，考虑N=3时，得到

(40)

其中:

(41)

因此，我们可以获得KE方程的3-孤子解:

(42)

3 结论

笔者利用达布变换求出KE方程的N-孤子解，首先从一个特殊的Lax对开始，从零解构造了一个非平凡的单孤子解，再从单孤子解构造出双孤子解，最后利用达布变换求出N-孤子解表达式.