水下无线传感器网络节点部署优化研究

孙宇晶

（沈阳化工大学，辽宁 沈阳 110000）

0 引 言

水下无线传感器网络（Underwater Wireless Sensor Network, UWSN）通常由规定的水下环境区域内一种或多种不同类型的传感器节点构成，这些不同种类的传感器节点一般会利用自身移动或人工的方式部署，最后实现特定的组网模式，并对该规定区域内的信息进行采集、收集和整理[1-2]。相较于陆地上的通信环境，水下环境较为复杂，其数据传输可靠性差，通常为了保证节点数据信息的成功传输，往往需要重发数据，此举使节点能量消耗过快，不仅提高了节点的部署成本，也会导致网络的连通率下降。因此在水下无线传感器网络的覆盖控制问题中，节点的部署至关重要。传感器节点部署将直接影响到节点能耗问题以及监测信息的准确性[3]。许多学者针对水下节点部署问题展开了研究，文献[4]针对节点的随机部署方式结合泰森多边形和狄洛尼三角法提出了基于深度调节的水下无线传感器网络节点部署方案，实现了大覆盖率及连通率，延长了网络生命周期；文献[5]主要针对移动受限节点部署方式产生的问题，提出了基于不均匀分簇半径可调的自部署算法，该算法不仅提高了网络性能，更提高了网络覆盖率。文献[6]研究了深度调节机制下的水下无线传感器节点部署优化算法，采用确定性感知模型，以沃罗诺伊多边形面积实现对目标区域的分层覆盖，以保证覆盖率；文献[7]融合智能鱼群算法提出了一种基于黏性流体算法的节点部署优化策略，该算法有效提升了覆盖度和均匀度。Yuanming Ding等人提出了基于移动节点部署的UWSNs双覆盖算法，该算法不仅保证了覆盖率并且减少了节点的能量消耗[8]。通过相关文献可知，优化水下无线传感器网络节点部署问题一般分为2个方向，即在不影响网络性能的前提下减少节点数量或是在节点数目固定的情况下优化网络结构，使得网络性能达到最优。

1 系统模型

1.1 节点感知模型

节点感知模型分为确定性感知模型、概率性感知模型，一般用于表达节点感知周围环境的能力。不同场景需要用到不同的感知模型。本文研究的环境为复杂的水下，因此采用确定性感知模型中的0-1感知模型。在二维平面中，0-1感知模型的感知范围为一个圆盘区域，假设一个节点作为其圆心，节点的感知半径为R，处于圆之外范围的节点皆无法被感知。0-1感知模型如图1所示。

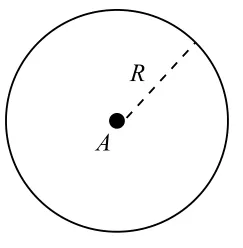
图1 0-1感知模型

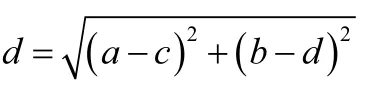
1.2 网络拓扑模型

Katti等人分析研究了水下无线传感器网络拓扑结构，如正方形网络结构、三角形网络结构以及六边形网络结构相对应部署方式的覆盖度和所需传感器节点个数。结果显示，三角形网络拓扑结构的覆盖范围更广，但相对所需节点数目也更多，部署成本较高；六边形网络拓扑结构所需部署的节点较少，但其数据传输不可靠；正方形传感器部署方案在节点个数和覆盖度两方面性能较平均。本文采用的网络节点部署优化指标为覆盖率和传感器节点数目。

2 算法设计

利用遗传算法求解上述优化问题的搜索空间为2N×N，其中N×N为网格点的数量，这是一个NP难题[9]。针对这一问题，我们可以利用遗传算法进行求解。本文中的传感器部署模型为0-1模型，非常适合使用二进制编码。在求解过程中，分别以网络节点数和覆盖率作为适应度函数对该问题进行求解，具体求解流程如下。

Step1：首先对传感器网络中的参数进行初始化，其中包括网格数量、格点间距离、网格类型、传感器覆盖范围等参数，然后对遗传算法中涉及的相关参数进行初始化，其中包括遗传算法的选择函数、变异概率和交叉方式等。

Step2：计算种群中个体的适应度函数，并计算个体是否满足覆盖率和传感器个数等条件，符合要求的个体，其适应度函数保持不变；不符合要求的个体，其适应度函数需要进行相应的修正。

Step3：根据适应度函数的大小对个体排序，选择相应的个体两两交叉，将得到的新个体放入下一代种群中，最后对该种群进行变异操作。

Step4：检查当前迭代数是否达到预设的最大迭代次数，如达到，则算法终止，否则跳到Step2。

算法流程如图2所示。

图2 算法流程

3 仿真实验

为验证本文所提算法的可行性，采用MATLAB a2015版本的软件进行仿真。在覆盖率给定时，需部署的传感器节点数量可利用遗传算法优化。假定水下二维目标水域的面积为90 m×90 m，把该区域划分为10×10的网格，需覆盖的目标位置在网格点上。假定该传感器网络在部署后需满足的覆盖率要求分别为90%、85%、80%和75%，将传感器部署在三角形划分的网格点上，其覆盖半径为12 m。设置初始种群为50，算法的最大迭代次数为200次。通过锦标赛法选择算子，交叉算子为两点交叉，变异算子的变异概率为50%。对个体进行随机初始化，0表示该位置未部署传感器，1表示该位置部署传感器，单个个体为10×10的0-1传感器部署矩阵。

将传感器的覆盖率作为适应度函数。当覆盖率满足要求时，适应度为传感器节点个数；当覆盖率不满足要求时，须对适应度函数进行修正，适应度=传感器节点个数/覆盖率。

目标覆盖率分别为92%、90%、84%、76%时，算法的优化过程以及传感器部署如图3～图6所示。

从图3（a）可以看出，在初始的100个迭代过程中，适应度函数降低较快，而在迭代后，最优适应度将不再变化。从图3（b）传感器部署图可以看出，最终的传感器部署仍存在部分冗余，这是因为初始种群数较低，增加初始种群个体数可以优化最终结果，但是计算时间将呈指数级增加。

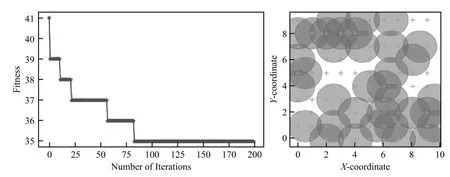
图3 覆盖率为92%时算法的迭代优化过程及传感器部署位置

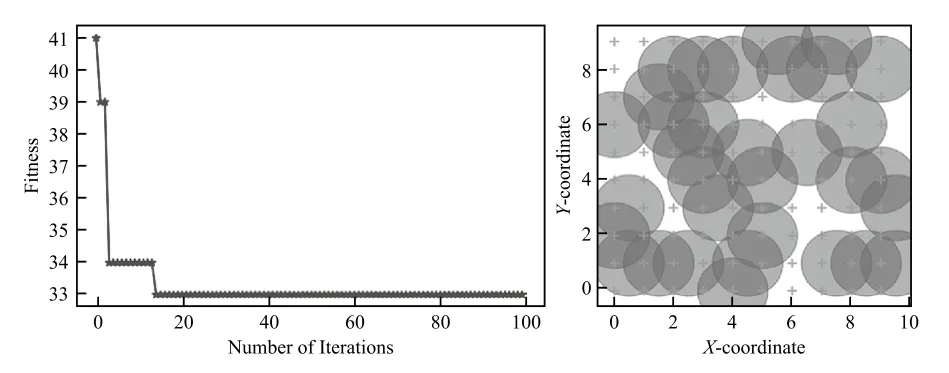
图4 覆盖率为90%时算法的迭代优化过程及传感器部署位置

图5 覆盖率为84%时算法的迭代优化过程及传感器部署位置

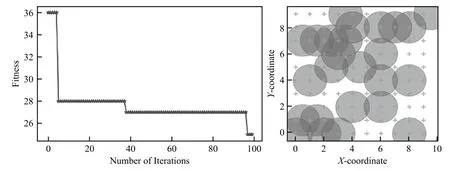
图6 覆盖率为76%时算法的迭代优化过程及传感器部署位置

4 结 语

从上述结果可以看出，本文设计的遗传算法具有快速收敛的特性，可以降低计算量和计算时间。当单个传感器的覆盖半径减少时，要保持覆盖率不变则需要增加传感器个数。当传感器的覆盖半径略大于网格点距离时（r＞d），传感器的利用效率较高。当传感器的覆盖半径变为d＜r＜2d时，传感器数量减少不明显，但网络覆盖范围会随r的增加而增大。