基于卷积网络和对抗式学习的雷达信号识别算法
2021-04-26何重航刘佳琪王宪栋刘洪艳
何重航,刘佳琪,王宪栋,刘洪艳,高 路
(1.北京航天长征飞行器研究所,北京,100076;2.试验物理与计算数学国家重点实验室,北京,100076; 3.中国人民解放军61336部队,北京,100094)
0 引 言
雷达是现代电子战中的关键作战装备,雷达信号的脉内调制特征分析是电子战领域一个重要研究内容,主要分析方法有时域自相关法、相位差分法和时频分析法。其中时频分析法是描述雷达信号在时域-频域二维平面上能量分布,以图像形式直观表现不同调制类型,常用的时频分析法有短时傅里叶变换、魏格纳-威利分布[1]、Choi-Williams分布以及平滑伪魏格纳-威利分布[2]等算法。常用的脉内调制识别的工作流程是通过时频分析法得到信号时频图像,再对时频图像进行特征提取得到特征向量,最后利用对特征向量实现对信号脉内调制的识别。随着人工智能、机器学习等技术的发展,卷积网络等一系列网络模型[3~6]在图像分类、人脸识别和目标检测等领域表现出优异的图像特征提取能力。文献[7]采用深度自动编码器结构,文献[8]采用卷积网络模型,两者都实现了脉内调制特征的识别,但是模型性能易受噪声影响;为解决信号低信噪比的问题,文献[9]采用更深层次的网络模型,文献[10]则采用多路通道的深度卷积神经网络,两者对低信噪比信号均具有较好的识别能力;文献[11]和文献[12]均采用多种图像特征融合的方法提高信号识别准确率;文献[13]则提出集成学习的方式,集成多种卷积网络提取的调制特征,文献[14]则将多个模型知识进行迁移,2种算法对低信噪比样本仍保持高准确率。
上述时频图像加网络模型的方法,在训练数据丰富情况下,具有良好的雷达信号识别性能,但现代战争对于电磁频谱资源管控严格,网络模型学习样本有限,且时刻面临新出现的信号样本,需通过学习新样本保持和提升识别性能[14~16]。针对新样本再学习的问题,本文提出一种基于卷积网络和对抗式学习的雷达信号识别算法,网络对新样本进行对抗式学习,在学习训练过程中网络各层参数自适应调整,从而实现对卷积网络的微调和更新,提升模型对新样本的识别率。
1 系统模型架构
1.1 信号模型
雷达脉冲信号可看作是信号和噪声两部分组成,其数学表达式为
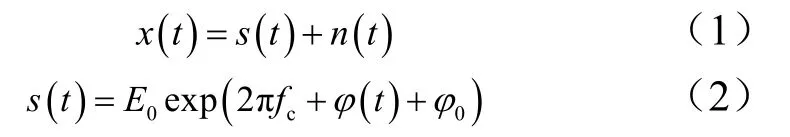
式中s(t)为雷达脉冲信号;n(t)为高斯白噪声;E0为信号幅度;fc为信号的载频;φ(t)为信号的瞬时相位变化;φ0为信号初始相位。雷达脉冲信号的脉内特征包括无意调制特征和有意调制特征,本文主要考虑脉冲有意调制特征的相位调制和频率调制特征。本文主要讨论以下 9种雷达信号脉内调制方式的识别:线性调频信号(Linear Frequency Modulation,LFM)、非线性调频信号(Nonlinear Frequency Modulation,NLFM)、科斯塔斯调频编码信号(Costas)、巴克码信号(Barker)、弗兰克编码信号(Frank)和4种多相编码信号(P1、P2、P3、P4)。
1.2 系统架构
系统工作流程主要分为 3步:模型预学习、模型再学习、模型应用。工作流程如图1所示。
第1阶段为模型预学习。结合新的深度可分离卷积方式,设计构造卷积神经网络,采用旧样本训练网络模型,将提取的信号时频图像特征,通过分类器初步实现对 9种雷达信号样本的识别,并保存卷积网络模型结构以及各层隐含参数。
第2阶段是模型再学习。采用对抗式学习的训练方式,将同样结构的卷积网络模型作为生成器,将旧样本数据标记为正标签,新样本数据标记为负标签,输入卷积网络模型和判别器,训练判别器;判别器训练完成后固定判别器参数,将新样本标注为正标签,训练卷积网络模型的隐含参数,使提取的新、旧样本特征向量相似,完成对生成器的训练。
第3阶段是模型应用。将新样本测试数据输入参数更新调整后的卷积网络模型(生成器),实现对新样本信号的识别。

图1 算法流程示意 Fig.1 The Structure of Algorithm
2 雷达信号时频变换
雷达信号数据通常是由采样得到的复数序列,包含丰富的时频域信息。通过时频变换的分析方法,将雷达脉冲信号的调制特征有效提取出来,变换形成信号时频图像。本文采用平滑伪魏格纳-威利分布的变换方式,能够较好抑制噪声导致的交叉项影响,平滑伪魏格纳-威利分布变换的表达式为

时频分布方法能够较好描述不同调制信号的能量在时间-频率坐标轴上的二维分布,将变换后图像进行灰度化作为网络模型输入,如图2所示。

图2 雷达脉冲信号时频分布 Fig.2 Time-frequency Transformation of Radar Pulse Signal
3 深度卷积神经网络
卷积网络最核心的是卷积层,由卷积运算代替传统矩阵乘法运算,提取输入图像特征。深度卷积网络模型层数越多、规模越大,提取特征的能力就越强,需要的内存资源也就越多,训练难度也更大,为了权衡网络模型特征提取能力和模型规模,借鉴具有代表性的 MobileNet网络的深度可分离卷积单元(Depthwise Separable Convolution),构造深度卷积网络模型。深度可分离卷积单元是卷积操作拆分为深度卷积(Depthwise Convolution)和逐点卷积(Pointwise Convolution)。深度可分离卷积操作是对每一个通道采用不同的卷积核进行卷积,再采用逐点卷积将多个通道输出进行拼接。深度可分离卷积单元的基本结构如图3所示。

图3 深度可分离卷积 Fig.3 The Depthwise Separable Convolution
标准卷积操作中卷积核尺寸为K×K,M为输入通道数,N为卷积核个数;深度可分离卷积中,深度卷积的卷积核尺寸是K×K,通道数为M,卷积核个数为1;而逐点卷积中卷积核的尺寸为1×1,通道数为M,卷积核个数为N。最终卷积的整体效果与标准卷积没有差异,但是极大的减少了计算量和模型的参数量。
卷积网络模型参数如表1所示。当模型中深度卷积的步幅为2时,可实现对输入特征图的降采样,最终通过平均池化操作将特征图尺寸变为1×1,由全连接层(fc1)输出特征向量,最终特征向量经过激活函数(Softmax)层,实现对9种雷达信号的分类。

表1 卷积网络模型参数 Tab.1 The Parameters of CNN Model
4 模型再学习
生成对抗网络(Generative Adversarial Network, GAN)主要包括生成器G(Generator)和判别器D(Discriminator),通过生成器与判别器的对抗式训练,使得生成器产生的生成样本尽可能与真实样本相似。本文,将旧样本经过卷积网络全连接层输出的特征向量看作真实样本,标注为正标签;将新样本经过卷积网络输出的特征向量看作生成样本,标注为负标签,输入为新样本的卷积网络则看作是生成器,判别器则是采用三层全连接层构成,判别器的结构如表2所示。

表2 判别器结构和参数 Tab.2 The Structure and Parameters of Discriminator
在训练过程中,需要判别器能够准确分出新、旧样本的特征向量,所以判别器D的损失函数为

式中x为旧样本信号的时频图像;z为新样本的图像;C表示已训练卷积网络模型;G表示再学习的网络模型(生成器);D(C(x))为判别器对旧样本特征向量的分类;D(G(z))为判别器对新样本的特征向量的分类。判别器可准确分辨2种特征向量,则D(C(x))接近1,判断旧样本特征向量为正类;D(G(z))接近 0,1-D(G(z))接近 1,判断新样本特征向量为负类。D(C(x))和 1 -D(G(z))分别取对数并相加作为判别器损失函数,最大化损失函数使判别器具有分辨能力。
生成器的损失函数如式(5)所示,生成器的目的是使判别器将由生成器得到的特征向量误判为正标签,判别器输出D(G(z))接近1,1 -D(G(z))接近0,最小化生成器损失函数使生成样本与真实样本差异最小。
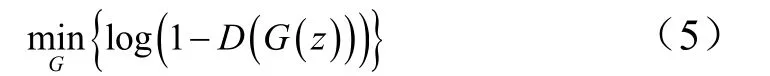
综合式(4)、式(5),生成对抗训练总损失函数:

4.1 判别器训练
通过模型预学习得到具有识别能力的网络,将网络模型所有参数固定不变,最后由全连接层(fc1)输出特征向量。通过网络模型分别提取旧样本特征向量标注为正标签,提取新样本特征向量标注为负标签,将正负样本输入判别器进行训练,训练过程如图4所示。在训练过程中采用反向传播算法将梯度传递到判别器各层,更新判别器的各层隐含参数,提高判别器新、旧样本的判别能力。
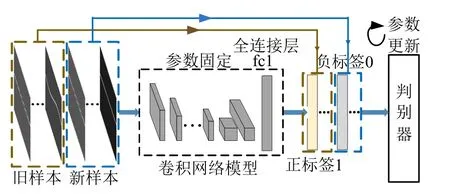
图4 判别器训练示意 Fig.4 The Training Procedure of Discriminator
4.2 生成器训练
生成器训练见图5,将新样本的特征向量均标注为正标签。通过反向传播算法将误差梯度传递到生成器中,更新生成器各层隐含参数。生成器和预训练模型结构完全相同,在生成对抗训练过程中,判别器和生成器进行交替训练更新,最终完成对生成器各层参数的更新,判别器分辨生成器输出特征向量的正负。
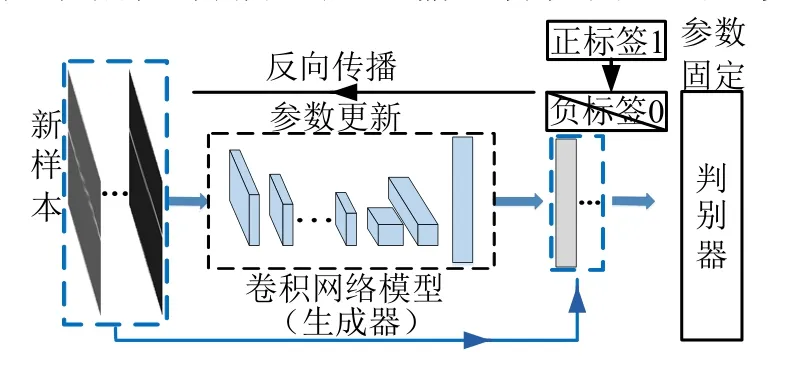
图5 生成器器训练示意 Fig.5 The Training Procedure of Generator
5 仿真试验分析
5.1 样本设置
9种不同调制方式的雷达脉冲样本数据具有相同的采样频率fs=256 MHz和相同的采样点数Ns=512,脉冲宽度τ=2 μs,脉冲信号调制参数设置情况见表3。
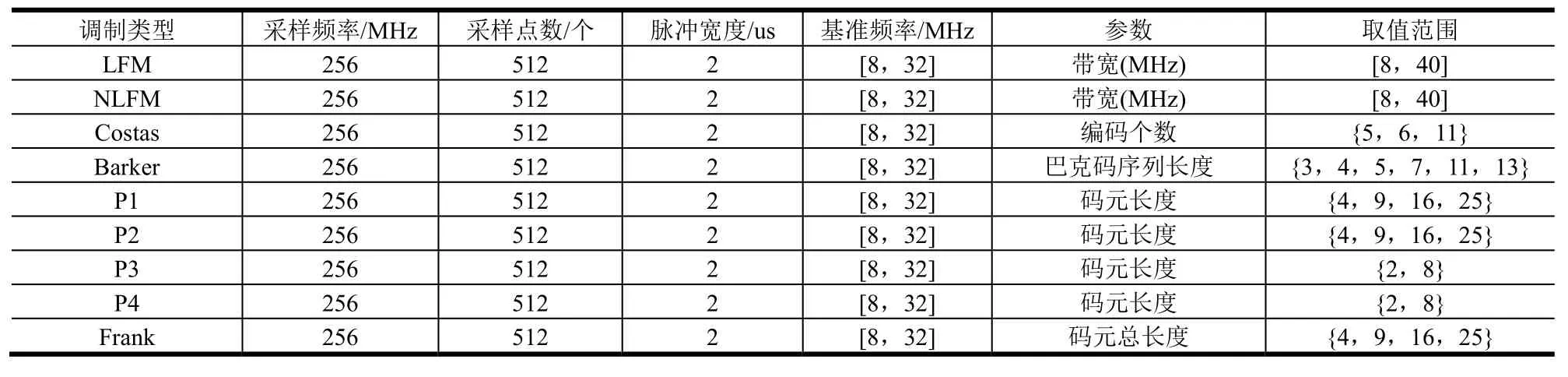
表3 脉冲信号样本参数 Tab.3 The Parameters of Pulse Signal Sample
每种调制类型 1000样本,信噪比分别设置为-4 dB、-2 dB、0 dB、2 dB、4 dB,每种信噪比下样本总数为9000,其中60%样本作为训练集,10%作为验证集,30%作为测试集。
5.2 仿真分析
a)模型预学习。
选择信噪比为0 dB样本集作为预训练数据集,输入模型的每一批样本数量为 12,迭代步数为 200;选择基于Adam算法的优化器,学习率设置为0.0001。模型训练过程如图6所示。

图6 卷积网络训练过程 Fig.6 The Training Procedure of CNN
训练后,模型对0 dB样本的测试集数据识别准确率为94.96%,测试样本的混淆矩阵如图7所示。
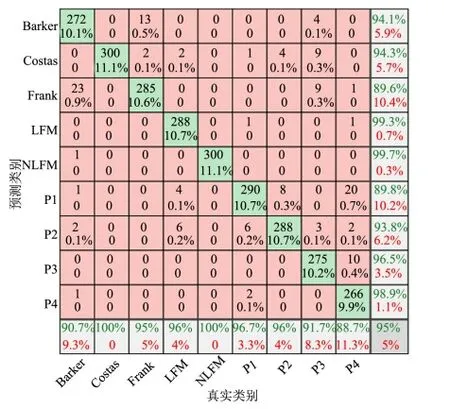
图7 0dB信噪比样本混淆矩阵 Fig.7 The Confusion Matrix of Samples at 0dB SNR
根据图7的混淆矩阵分析,在信噪比为0 dB条件下,模型整体具有较高的准确率,基本完成对LFM和NLFM信号的正确分类。因为Frank信号、Barker信号, P1、P2、P3和P4多相编码信号均为相位编码调制方式,所以信号时频图像较为相似,存在较多的误分类情况。
b)模型再学习。
将模型预学习中 0 dB信噪比样本作为旧样本数据,选择信噪比-4 dB、-2 dB、2 dB、4 dB 样本集作为新样本对抗式训练,训练中每一批输入样本数量为15,迭代步数为50,判别器和生成器优化均采用Adam算法优化器进行优化。训练前后模型的识别率见表4和图8。

表4 不同信噪比样本识别率 Tab.4 The Recognition Rate of Samples at Different SNR
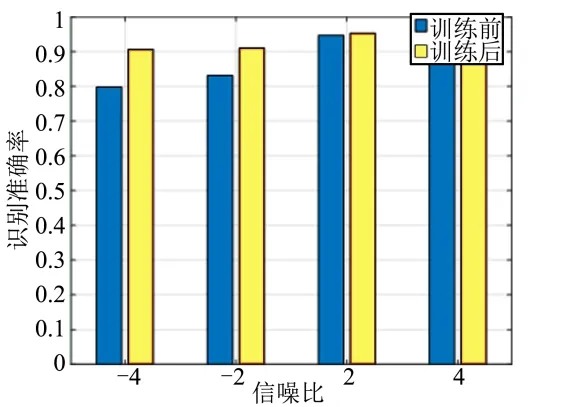
图8 不同信噪比样本识别率 Fig.8 The Recognition Rate of Samples at Different SNR
根据表4和图8分析,对于信噪比为-4 dB和-2 dB的新样本,经过对抗式训练后,更新了网络模型参数,识别准确率得到明显提高。进一步分析低信噪比条件下模型参数更新前后模型性能的变化,将对抗式训练前、后-4dB样本测试集的混淆矩阵进行对比(见图9)。
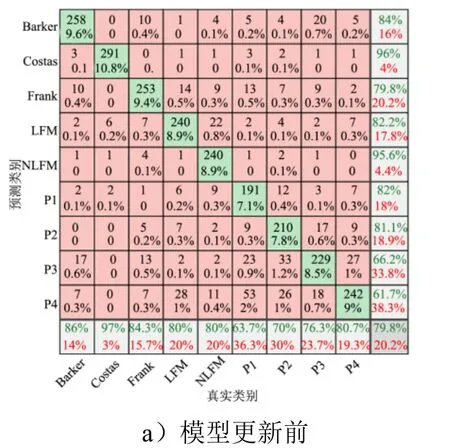
图9 -4dB信噪比样本混淆矩阵 Fig.9 The Confusion Matrix of Samples at -4dB SNR
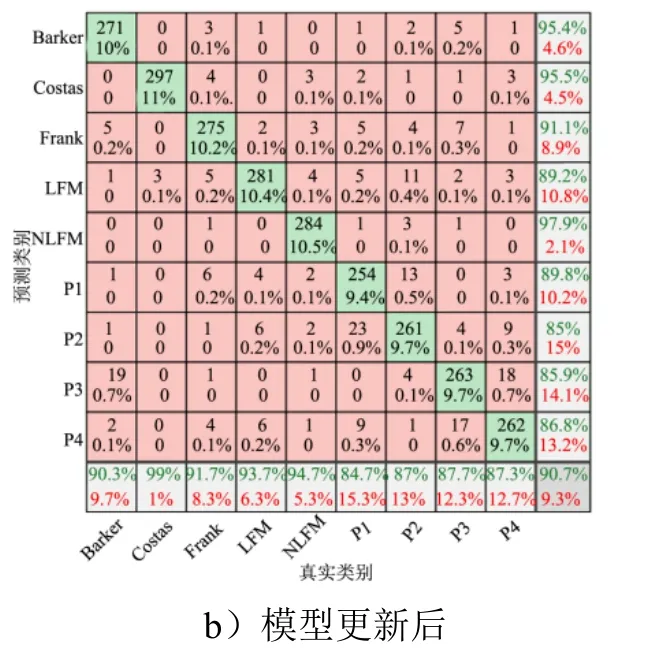
续图9
根据图9的混淆矩阵,-4 dB信噪比样本由于噪声影响,预训练的模型难以有效提取时频图像特征,对新样本存在较多的误分类。模型经过对抗式再学习后,对新样本整体准确率得到提高,试验结果表明经过对抗式学习后网络对低信噪比信号识别能力得到提升。
6 结束语
本文提出了一种基于卷积网络和对抗式学习的雷达信号识别算法,以对抗方式自适应调整、更新卷积网络模型参数,提高了网络模型对新增信号数据的学习能力,对-4 dB信噪比新样本的准确率提高了10.89%。为电子对抗、雷达对抗提供了坚实的技术支撑,也可以推广应用到通信信号等其他类型信号的识别领域。
