基于高斯伪谱法和有限差分结合的飞行器 燃料最优轨道转移优化

周珺仪，刘佳琪，焦胜海，段红亮，陈晓光

（1.北京航天长征飞行器研究所，北京，100076；2.试验物理与计算数学国家级重点实验室，北京，100076）

0 引 言

随着战场态势的日趋复杂，空间任务逐渐多样化，要求飞行器能够在短时间内快速完成多项任务。因此需要运载器在携带有限燃料的条件下，具备快速、多次机动至不同轨道完成任务的能力，且每次任务消耗的燃料越少，运载器能够执行的任务越多，其作战能力就越强。为了提高燃料的有效利用率，飞行器必须根据任务目标，自主规划燃料最优变轨方案。

燃料最优变轨[1～3]作为一个连续过程的优化问题，其本质是泛函求解极值的问题。常用的方法有直接法、间接法和混合法。直接法是对参数进行离散化，将问题转化为参数优化求解；间接法是基于极小值原理，将问题转化为两点边值求解；混合法则是将问题转化为具有约束的参数求解，用非线性规划方法进行求解。

伪谱法作为经典的直接优化法，已经广泛应用于深空探测卫星轨道优化[3]、临近空间高超声速飞行器制导优化[4]、日-火Halo转移轨道快速优化设计[5]、二级助推火箭多阶段轨迹优化[6]等领域。间接法[7～10]计算精度高，包括用于最优月球软着陆轨道的隐式打靶法、轨道转移的多重打靶法、全电推进卫星轨道优化的同伦解法等。

伪谱法收敛速度快，但控制曲线存在突变，不能直接应用于工程；有限差分法作为间接法的一种，结果精度高，但对初值猜测敏感，初值猜测误差过大会导致发散。为了能够快速得到任意空间任务需求下燃料消耗最少的精确轨迹，本文将高斯伪谱法和有限差分法结合，进行小推力变轨优化设计，提出考虑任务规划下常值推力短时间快速变轨最优燃料消耗的精确解，并给出相应的仿真结果。

1 模型建立

1.1 飞行器运动学模型

假设飞行器在中段飞行过程处于瞬时平衡状态；忽略除发动机推力之外的摄动，飞行器控制系统处于理想工作情况，不存在延时，则小推力飞行器动力学模型[3]为

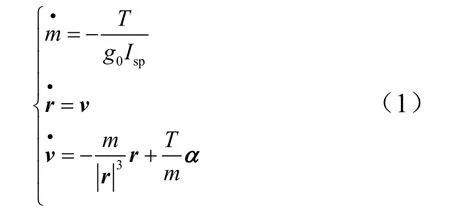
式中m为飞行器总质量；T为发动机推力大小；g0为重力加速度；Isp为比冲；r为飞行器的位置矢量；v为飞行器的速度矢量；α为推力方向的单位矢量。

1.2 高斯伪谱法

高斯伪谱法[1～6]本质上是在一系列配点处将状态变量和控制变量进行离散，并以离散点构造全局拉格朗日插值多项式来近似系统动力学方程，从而将连续的最优控制问题转换为非线性规划问题。

a）时域变换。

伪谱法求解时域为[-1，1]，因此要将实际求解时间[t0,tf]进行变换，引入转换变量τ∈[-1，1]，即：

式中t0为求解初始时刻；tf为求解末时刻。

b）状态变量x()τ、控制变量u()τ离散化。

通过对选取的高斯点构造插值多项式对连续状态变量x()τ、控制变量u()τ进行逼近，即：

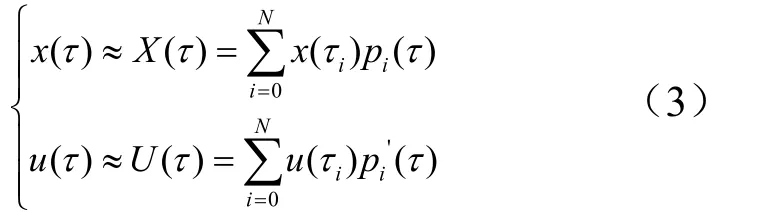
式中pi(τ)为插值基函数，插值基函数及其求导结果为：

c）状态方程转换。

状态变量x()τ对时间τ进行求导，将动力学方程转换为代数方程，即：

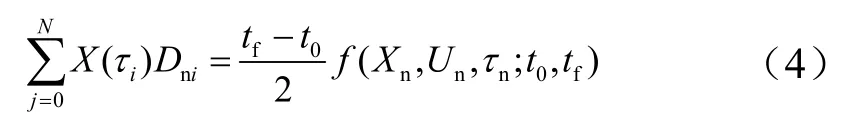
式中Dni为离散矩阵元素；f(Xn,Un,τn;t0,tf)为运动学方程。

d）目标函数。

对于燃料最优问题，存在目标函数：

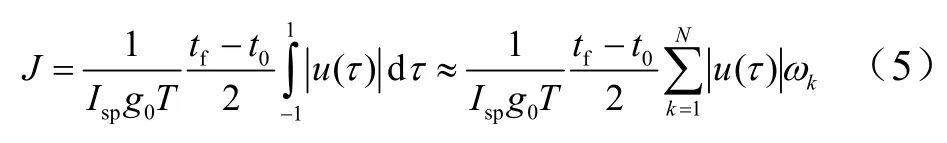
式中ωk为高斯权重系数，k= 1 ,2,…,N。

e）转换为NLP问题标准模式。

通过上述过程，将连续泛函最优控制问题转换为离散形式的NLP问题：

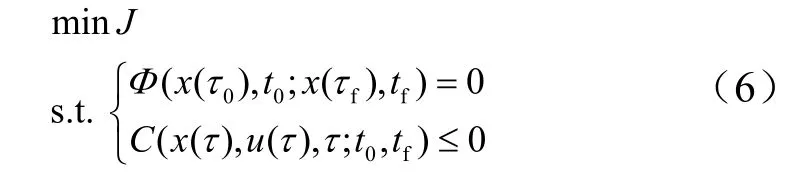
式中J为性能指标函数；Φ为边界条件；C为不等式约束条件。

1.3 燃料最优间接法

燃料最优性能指标：

根据最优控制理论，引入哈密顿函数：

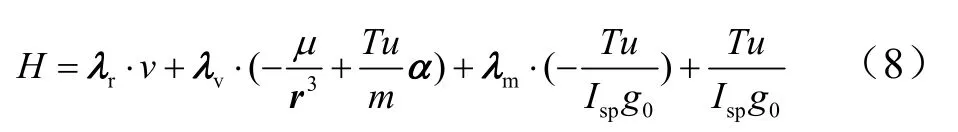
式中rλ，vλ，mλ均为协态变量；μ为引力系数。

由极小值原理，推出：

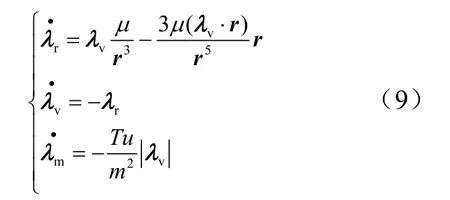
带入哈密顿函数，推出推力最优控制函数：

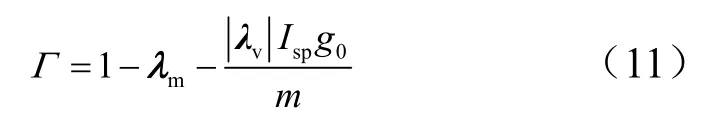
2 轨道优化方案设计

本文以飞行器多次自主机动进行轨道位置转移为研究背景，仿真选取 2个机动目标位置、一次实施机动变轨为例进行轨道位置转移分析优化。

2.1 飞行任务规划

已知飞行器初始位置R0、速度V0及初始姿态，在飞行过程中期望于t1内由目标A位置机动变轨到目标B位置附近伴飞，并保持相对静止时长t2。

2.2 模 型

以轨道转移为例，目标需要在T内完成轨道转移以及姿态调整，假设t1∈[a,b]，飞行器完成轨道转移，到达指定的目标。则终端约束条件为

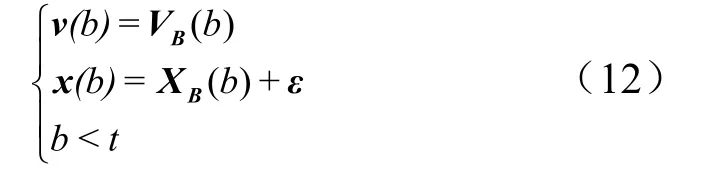
式中v(b)，x(b)分别为飞行器转移完成后在b时刻的速度和位置；VB(b)，XB(b)分别为b时刻惯性飞行器的速度和位置；ε为误差允许量。

控制量U=[αx,αy,αz,u]约束条件为

式中xα，yα，zα分别为推力沿x，y，z3个方向的分量；u为发动机控制量。

性能指标取燃料最优，有：

式中mf为飞行器燃料消耗质量。

2.3 优化模型

2.3.1 初值猜测

简化飞行器运动模型[11]：

引力加速度采用平方反比引力场模型时，对于飞行器位置变换，引力加速度变化不大，因此采用平均引力假设来近似引力计算。

对于常值推力发动机，最短时间飞行问题可以等价于燃料最优，因此，最优控制性能指标简化为

因此，对于伪谱法求解最优燃料消耗问题时，控制量可以通过基于脉冲推力的轨道求解获得近似解，加快求解速度，具体过程如图1所示。

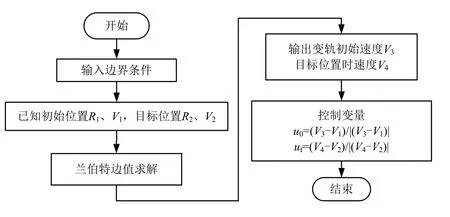
图1 优化过程 Fig.1 Optimization Procedure

2.3.2 有限差分法

最优控制模型可以简化为含未知参数的两点边值问题求解，针对本文求解14个方程组的边值问题，选择有限差分法进行优化。

考虑本文非线性方程组：

初始条件为

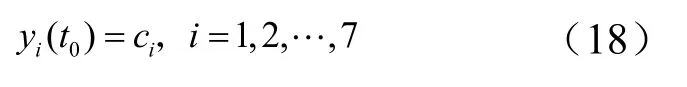
终端条件为

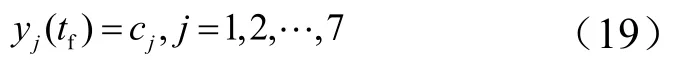
将区间t∈[t0,tf]等分为N个子区间，y(t)在ti处Taylor展开取t=ti+1=t+ih，忽略二阶以上部分，得一阶导数的前向差分近似：

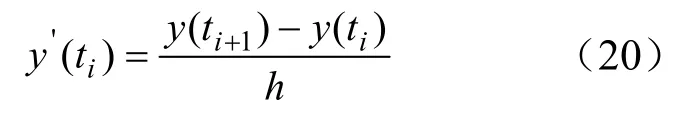
将区间离散化，在节点应用差分公式，得到新的代数方程组，以及方程组的近似Jocabi矩阵。

2.4 优化方案

优化方案如图2所示。

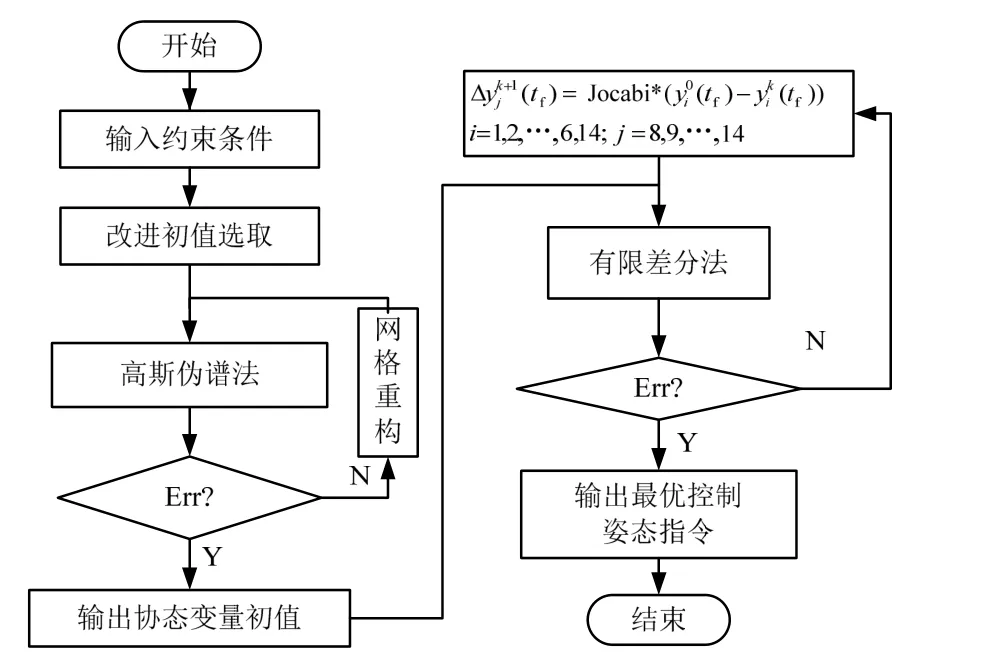
图2 优化方案 Fig.2 Optimize Process

如图2所示，首先，根据初始条件按Lambert问题求解近似控制变量初值，并将求得的变量初值带入Gauss伪谱法求解方程，取误差小于10-4快速求解协态变量近似值。然后，将求解的协态变量近似初值和初始状态变量带入间接法构成的边值问题进行求解，通过有限差分法继续优化。当满足精度要求时，结束优化，输出最优控制推力、姿态指令。

3 仿真校验

3.1 场景设定及参数设置

假设初始时刻有2个飞行器A、B，A和B相距5 km（方向随机设定），A、B逐渐拉开距离。C飞行器在初始时刻于A附近伴飞，要求C飞行器6 s后向B飞行器转移，40 s内完成轨道转移在B飞行器附近伴飞。

飞行器参数见表1。

表1 飞行器参数Tab.1 Aircraft Parameters

3.2 仿真结果

C飞行器40 s完成轨道转移后，飞行器剩余质量830.3 kg。仿真得到推力沿x、y、z三轴的控制变量同发动机开关控制量随时间变化的关系如图3a所示；飞行器质量变化同发动机开关控制量随时间变化的关系如图3b所示，发动机开机时间燃料持续消耗，飞行器质量呈线性下降，发动机关机时间，无燃料消耗，飞行器质量不变；飞行器的优化轨迹如图3c所示，飞行器在起始阶段发动机工作向预定目标轨道转移，中间发动机关机自由飞行，到预定目标附近发动机再次工作实现伴飞（图3中实线为控制变量，虚线为发动机控制量）。

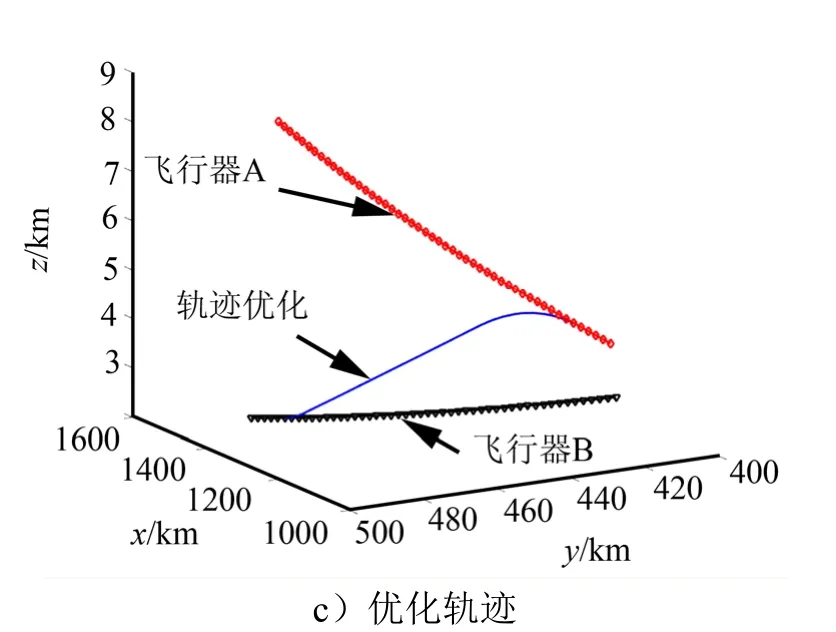
续图3

3.3 仿真验证

根据3.2节的仿真实例，采用高斯伪谱法同本文优化方案进行对比，验证本文方案能够快速收敛，能够应用于在线规划燃料最优转移轨道。表2为不同优化方案的结果、计算速度对比。通过表2可以发现，采用本文提出的优化方法，改进初值后的计算时长比随机初值的高斯伪谱法大大缩短，减少了计算量。同时，3种方法的飞行器剩余质量误差处于允许范围，验证了本文方法的准确性。

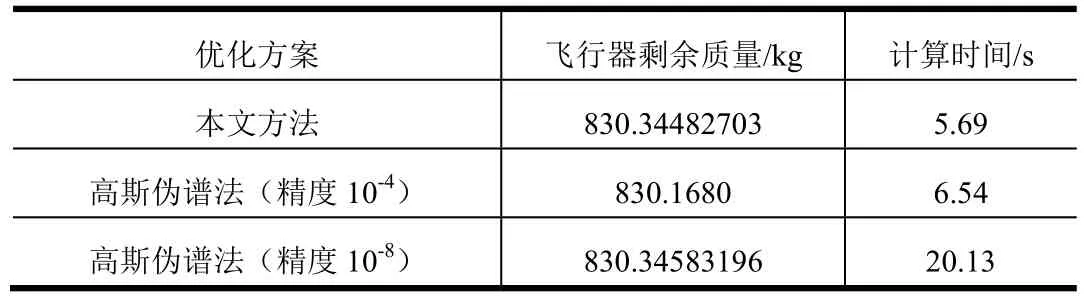
表2 方案对比Tab.2 Optimization Scheme Comparison

选取3种方法得到沿x轴的控制变量以及发动机开关曲线随时间的变化关系作为对比，仿真结果如图4所示（图4中实线为控制变量，虚线为发动机控制量）。

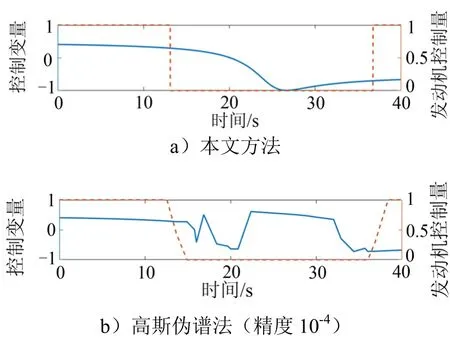
图4 x轴控制变量及发动机开关曲线变化关系Fig.4 Relationship between x-axis Control Variables and Engine Switch Curve

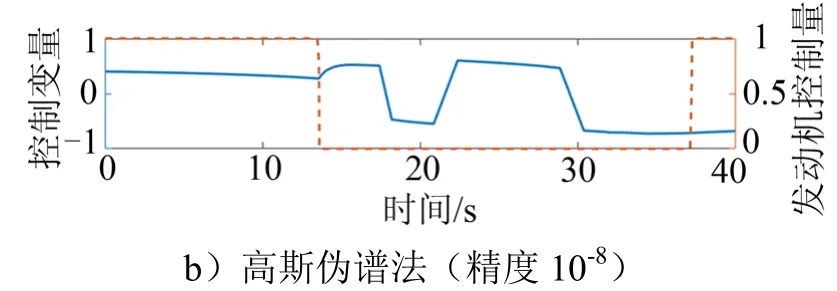
续图4

由图4可知，本文采用的结合法，控制曲线连续光滑；采用精度较低的高斯伪谱法，虽然能够快速计算出结果，但是推力控制曲线为变推力曲线，同实际情况不符，误差较大；采用高斯伪谱法同本文方法结果相差不大，但是曲线存在突变，计算时间过长，不能很好地适应快速变化的战场态势。

4 结束语

本文研究了飞行器在空间自主轨道转移优化的方法，提出了改进初值猜测的高斯伪谱法和有限差分法相结合的方法，分析了常值推力机动变轨燃料最优的轨迹优化问题，基于设定的场景和参数开展了轨道转移仿真分析。研究结果表明：相比高斯伪谱法，本文所用方法控制过程稳定无误差，收敛速度提高，计算结果精度更高，可满足战场空间任务快速、多样化的需求。