面对称结构战斗部破片特性能量分析方法

段 妍，赵红燕，张 健，周泽新，王骁峰

（1.空间物理重点实验室，北京，100076；2.北京宇航系统工程研究所，北京，100076）

0 引 言

近年来随着气动、控制等相关学科专业的高速发展，高速巡航导弹逐渐成为国内外导弹与飞行器研究的热点。这类飞行器的最大特点是飞行速度快、射程远、机动能力强和突防性能高。由于高速新型武器平台对机动类目标打击的军事需求，目前急需对基于此类武器平台的战斗部毁伤性能开展基础研究。

适应于高速飞行的需要，该类导弹的气动外形一般有别于常规速度的导弹和飞行器，通常为面对称结构。相应地，其战斗部舱段外形也往往具有面对称的特征，如近似为 D型的高爆战斗部[1]。针对高速飞行器舱段的外形特点，采用传统圆形截面战斗部结构将大大降低战斗部舱段的空间利用率。如果按照舱段外形匹配战斗部结构，则能够充分利用战斗部舱段的空间，设计出具有更大装填量和更大威力的战斗部，从而使此类高价值的武器平台发挥出更大的作战意义。因此，针对此类高速飞行器对战斗部的需求，需开展面对称复杂结构战斗部的毁伤特性研究，建立面对称战斗部毁伤过程的分析模型，为面对称战斗部毁伤能力分析及结构设计提供理论支撑。

传统的导弹通常为回转体结构，因而回转体也成为战斗部工程设计中最常用的结构，很多研究都是基于此类结构开展，早在1943年，Gurney[2]提出计算柱壳在炸药爆炸驱动作用下的速度公式；Charron[3]考虑了战斗部两端稀疏波的影响并对Gurney公式进行了修正；Lloyd[4]提出了有限长度柱壳Gurney公式，修正结果在Goto[5]和Lambert[6]的研究中得以成功运用；刘晋渤等[7]采用数值仿真的方法，对变锥度结构战斗部预制破片的飞散速度和飞散角度等特性进行了研究；Ning等[8]针对棱柱形破片战斗部的毁伤特性进行了试验及数值模拟研究，针对此类结构战斗部初速计算提出了修正的经验公式。然而对于三维复杂面对称结构战斗部而言，传统的工程方法难以满足精确计算战斗部毁伤威力空间分布规律的需求，针对其毁伤特性理论分析的研究还不够充分详实。本文建立了面对称结构战斗部的能量分析模型，采用修正的Hamilton原理求解面对称结构战斗部在爆炸载荷作用下的动力响应问题，得到结构变形的运动方程，并采用四阶Runge-Kutta方法进行求解，计算结果与地面静爆试验结果吻合较好，能够为战斗部的优化设计及威力评估提供理论依据。

1 结构分析模型

1.1 面对称战斗部结构特点

以棱柱型面对称结构为例，战斗部三维模型示意如图1所示。棱柱的3个侧面有1个面内嵌有刻槽钢板，用于在起爆过程中形成预控破片，另外 2个面为非破片面。战斗部上端盖为起爆端，下端盖为非起爆端。刻槽钢板通过螺钉与壳体连接。图1中虚线表示对称平面，定义战斗部对称平面上的破片列为中间列R0，对称平面两侧的破片列为侧列R±1,R±2。

图1 面对称破片战斗部示意 Fig.1 Schematic Diagram of Plane-symmetric Warhead

1.2 能量分析模型

内嵌刻槽钢板的面对称结构战斗部在内部炸药起爆后，壳体在爆炸产生的高压作用下迅速膨胀断裂，形成以高速破片为主的毁伤元作用于目标。整体结构可简化成由棱柱形装药、矩形刻槽钢板、铝合金侧板、上下铝合金端盖组成，如图2所示。刻槽钢板和铝合金侧板考虑其刚性位移和塑性变形，而端盖则假设成刚体，仅考虑其刚性位移。

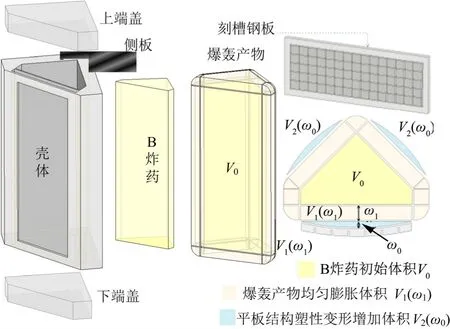
图2 面对称结构战斗部分析模型 Fig.2 Analytical Model of Plane-symmetric Warhead

图2给出了起爆后爆轰产物体积增加的示意，炸药初始体积为V0。假设起爆后产物均匀膨胀，则可计算出爆轰产物增加的体积V1(ω1)和V2(ω0)。其中V1(ω1)与壳体结构的刚性位移1ω有关，可根据装药形状计算得到。V2(ω0)则与板结构中心处的塑性变形量0ω有关，可根据板的变形构型计算得到。爆轰产物在任意时刻的体积可表示成式（1）的形式：

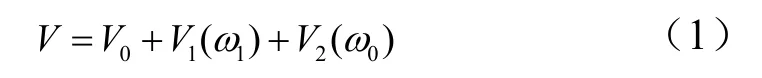
该模型从能量守恒的角度进行研究，即战斗部内装药爆炸过程中所释放出的总能量应消耗于如下几个方面：爆轰产物的内能、爆炸产物膨胀运动的动能、铝合金壳体和刻槽钢板的动能、壳体的塑性变形能。

a）爆轰产物能量分析。

爆炸产物总内能等于其质量与比内能之乘积，即：

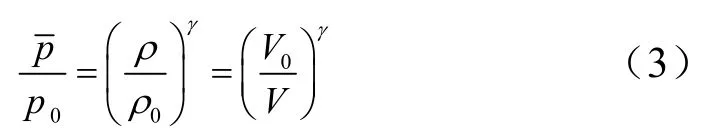
式中p0，0ρ分别为炸药初始状态的压力和密度，将式（3）代入式（2）：

鉴于：

式中Qv为炸药的爆热，在γ=3时，将式（1）、式（5）代入式（4）有：

以近似柱型装药对爆轰产物的动能进行计算，假设爆轰产物外边界的膨胀速度与壳体速度相等。战斗部爆炸后壳体由r0膨胀到rk，则产物体积变化为

式中h为平板厚度；r为壳体半径。

假设产物的膨胀速度v由装药中心到产物外边界rk达到最大速度v0，并且沿半径成线性分布：

由此，爆轰产物的动能可以表示为

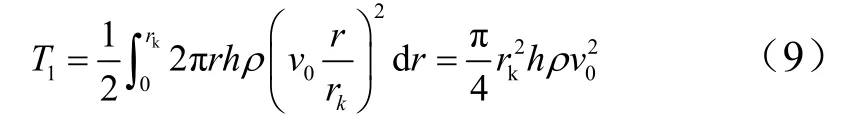
考虑到装药质量为

将壳体膨胀的速度1ω˙代入式（9），可把爆轰产物的动能表示为

b）壳体结构能量分析。

假设端盖为刚体，不考虑其塑性变形，端盖的质量为M，端盖的刚性位移为1ω，则端盖运动速度为1ω˙，端盖动能可表示为

刻槽钢板和铝合金侧板考虑塑性变形，位移有2个未知量：刚性位移ω1和板中心处的挠度ω0。对于矩形平板问题，采用薄板在小变形下的基本假设，若板的边长分别为2a和2b，则可给出平板的变形构型：

则变形壳体的位移和动能可分别表示为

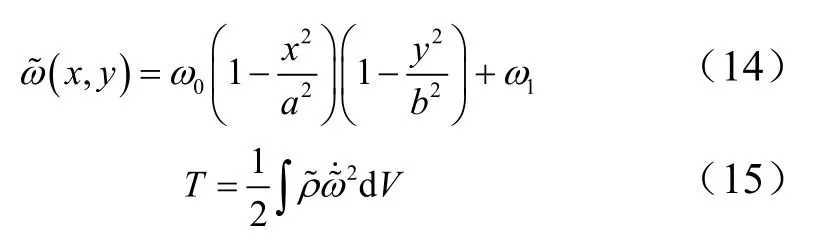
式中为平板密度；为变形壳体的速度。

计算壳体塑性变形能时，采用应变率无关理论，应用静态屈服条件及与之相关联的塑性流动法则，假定金属材料为理想钢塑性，采用弱相互作用的屈服条件为

式中0σ为金属的屈服强度。计算变形体的形变势能可以用应变能在整个变形体的体积上进行积分得到：

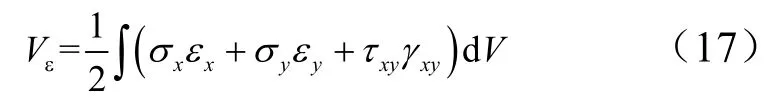
式中xσ，yσ，τxy为应力分量；xε，yε，γxy为形变分量。根据平板小挠度弯曲理论，可得到金属平板的塑性变形能为

2 动态响应分析

2.1 修正 Hamilton 原理

Hamilton原理可表述为：在2个瞬时t0和t1之间，描述物体真实运动的广义位移ξi（t）使得Hamilton作用量JH取驻值，即：

式中δJH为JH的变分；L为Lagrange函数，L等于系统的动能与系统的总势能之差：

式中Ω为体积域；S为面域；U为系统的变形能；Fbi为单位体积力做的功；为给定的边界力。

这是经典Hamilton原理，它适用于保守系统。对于非保守系统，如弹塑性系统则不能直接应用，做如下修改，即令修正的Hamilton作用量使下式成立：

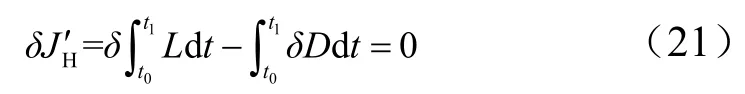
式中D为单位时间内系统的耗散能。对于弹塑性系统D则为物体的塑性功率，且：

式中Qj为广义力；为与广义力对应的广义应变率。式（21）即为修正的Hamilton原理，即在同一时间间隔内，在由系统的初始位置到达最终位置的所有与真实运动相邻近的可能运动中，真实的运动使泛函JH"取驻值[9]。

2.2 控制方程

根据面对称结构战斗部结构特点建立分析模型，令L=T-U，其中：T表示系统动能之和；U表示由炸药内能Ei和壳体变形能Vε组成的系统势能之和。由修正的Hamilton原理可得到：

式中qi为模型的运动参量。将模型各物理量代入上述各部分能量表达式中，可分别得到系统动能和势能的表达式：

式中T1为爆轰产物动能；T2为刻槽钢板动能；T3为铝壳动能；下标s和Al分别表示与刻槽钢板和铝壳侧板相关的物理量。将T和U代入式（23），则可得到关于战斗部壳体变形运动的控制方程，采用四阶Runge-Kutta方法可对其进行求解。

3 计算结果分析

采用地面静爆试验的方式，获取如图1所示战斗部破片速度分布规律。采用上述控制方程对其进行求解，计算结果与试验结果对比如图3所示。中间列破片R0初速最高，其次为侧列R±1，侧列R±2初速最低。除端部误差较大之外，其余误差都在 10%以内。由于分析模型中炸药采用了瞬时爆轰假设，刻槽钢板中心处破片速度最高，两端面呈现对称分布。而静爆试验中为端部起爆方式，起爆端破片初速整体略低于非起爆端，计算结果与试验测得的破片速度分布规律相比略有差异。但理论计算结果基本能反映出破片的速度分布特征，可以对面对称结构战斗部的破片速度和毁伤特性进行预测分析。

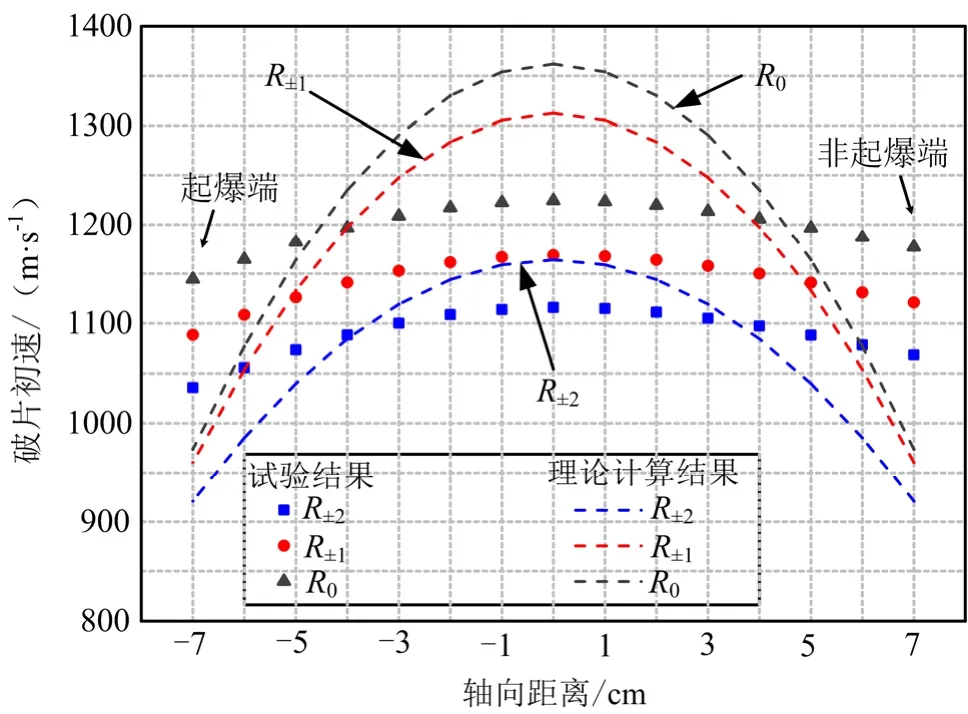
图3 理论计算结果与试验结果[8]对比 Fig.3 The Comparison Results between the Theoretical Calculationand Experimental Measurement

根据分析模型对战斗部壳体的变形运动过程进行分析，得到系统动能和势能占总能量比值随时间的变化，如图4所示。从图4中可以看出，在炸药爆炸驱动战斗部壳体变形的过程中，炸药的内能主要转化成了爆轰产物、壳体和破片的动能，破片的动能占到约20%，壳体的动能占到约 10%，而壳体的变形能所占比重很小，不足0.1%。

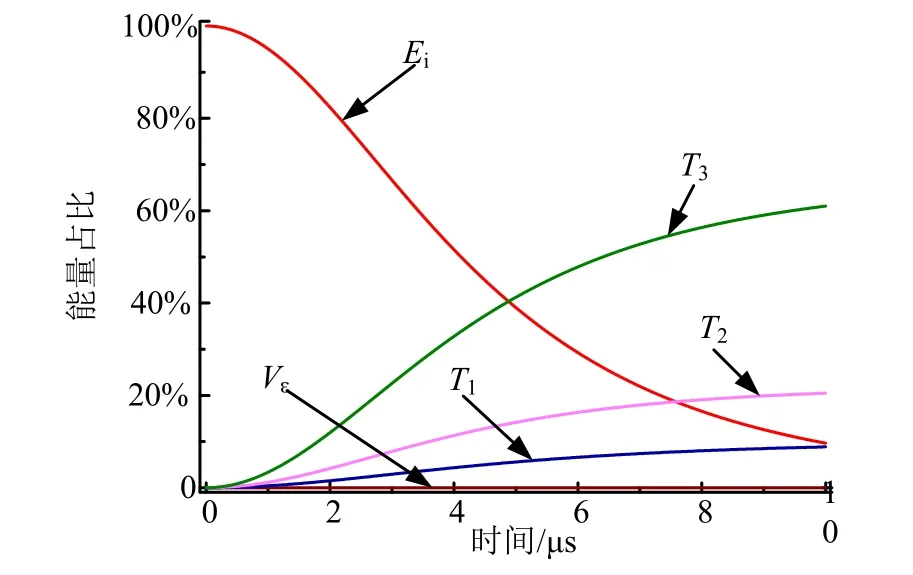
图4 系统各部分能量占比变化规律 Fig.4 Variation of Energy Composition of Every Part

图5为刚性运动速度1ω˙和变形速度0ω˙随时间变化曲线，图6为刚性位移1ω和塑性变形的最大位移0ω随时间变化的曲线。壳体刚性位移和速度增幅大于塑性变形位移和速度。随着炸药内能逐渐转化为壳体的动能和变形能，壳体刚性速度和变形速度逐渐趋于平缓。

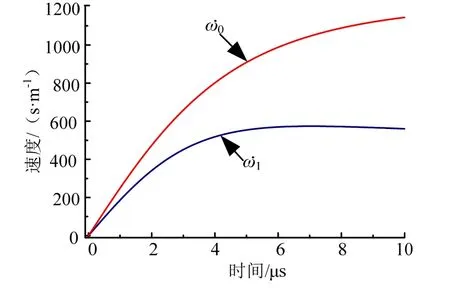
图5 刚性速度与变形速度变化规律 Fig.5 Variation of Rigid Velocity and Plastic Deformation Velocity

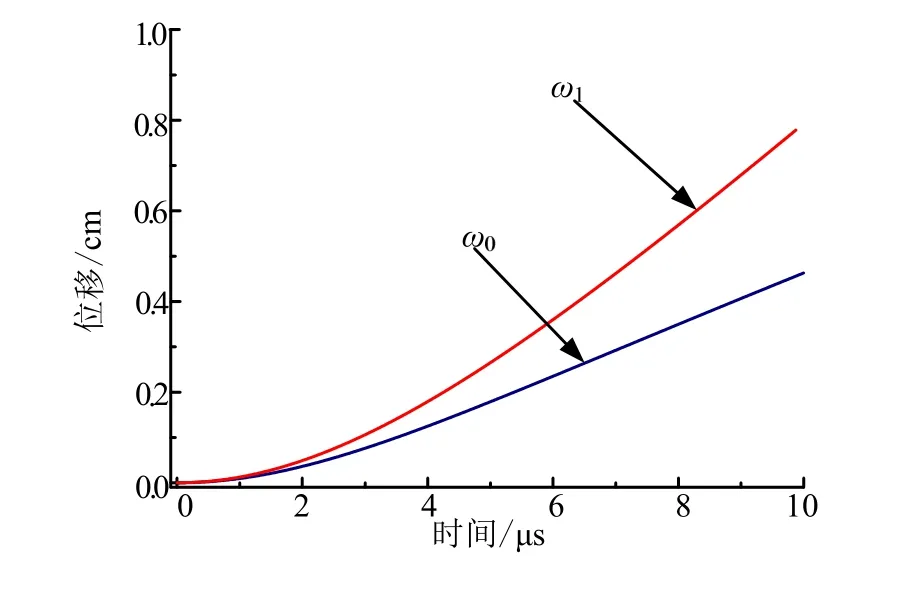
图6 刚性位移与塑性变形位移变化规律 Fig.6 Variation of Rigid Displacement and Plastic Deformation

4 结束语

本文基于能量分析方法建立了面对称结构战斗部在内爆加载作用下的动态响应过程的理论模型，基于修正的Hamilton得到壳体变形运动控制方程。通过求解控制方程得到壳体变形位移、破片初速及各部分能量随时间变化的规律，计算结果与试验结果吻合较好，验证了理论模型的合理性，对于面对称结构战斗部毁伤效能评估具有重要的理论价值和工程意义。