五相开绕组永磁容错电机零序电流开环容错控制策略

李琪琦，郑再平，李旭阳，杨 斌，王开春

（1.北京精密机电控制设备研究所，北京，100076；2.航天伺服驱动与传动技术实验室，北京，100076）

0 引 言

航空航天领域对可靠性有较高的要求，通常要求系统能够在发生故障后容错运行。多相电机在相数上的冗余可以在不改变硬件结构，只改变控制策略的情况下实现故障下的容错运行。因此，多相电机的容错控制策略成为国内外的研究热点。

目前，容错控制策略主要包括以磁动势不变为原则的容错控制策略和以转矩脉动最小为原则的容错控制策略。以磁动势不变为原则的容错控制策略又可以主要分为最优电流给定容错和降阶解耦矩阵容错[1]。以转矩脉动最小为原则的容错控制策略[2,3]和最优电流给定容错策略[4～6]通常在自然坐标系下通过滞环、PI或PR控制器跟踪交流电流实现。但滞环控制器开关频率不固定，PI控制器带宽有限，跟踪交流量的效果差，PR控制器结构复杂参数多，设计难度大。降阶解耦矩阵容错控制策略可以通过重构解耦矩阵实现在旋转坐标系下通过PI控制器跟踪直流量，因而受到广泛关注，Hyung-Min Ryu等提出一种正交的降阶解耦矩阵形式，采用该解耦矩阵进行坐标变换后电机故障下的数学模型与正常情况下几乎一致，只包含一相与转速无关的二倍频分量，可以视作扰动通过前馈抑制[7]。Hugo Guzman等学者针对五相永磁同步电机提出一种实现了故障后反电势幅值对称的不正交降阶解耦矩阵形 式[8]。赵美玲等构造了使磁场定向控制能够应用于容错状态的变换矩阵，通过解耦变换矩阵使得缺相后的电机电感、磁链矩阵对角化，从而实现了励磁电流分量和转矩电流分量的解耦控制[9]。但降阶解耦矩阵常会导致数学模型的不对称，需要额外的补偿措施。同时，故障相位置的不同，会导致降阶解耦矩阵和电机解耦变换后的模型的不同，增加了该控制策略的实现难度。

上述容错控制策略的研究多针对共中性点电机，即相电流和为零的约束必然存在，从而减少了一个控制自由度。本文的研究对象为采用陶瓷轴承的五相开绕组永磁容错电机，不存在相电流和为零的约束，同时陶瓷轴承阻断了零序电压形成轴电流的回路，不会对轴承造成损害。因而，可以通过4个控制自由度控制 4个相电流。基于开绕组容错电机的特点，本文针对一相开路故障下零序电流开环的容错控制策略开展研究，并进行仿真验证。

1 五相开绕组永磁容错电机的数学模型

多相永磁容错电机各相绕组间需满足电磁隔离的特点，因此定子通常设计为开绕组结构且各相互感为零。五相开绕组永磁容错电机主电路拓扑结构如图1所示。其中，OW-FPMSG为五相开绕组永磁容错电机，每相绕组与2个桥臂中点相连，构成一个H桥电路驱动一相绕组的形式，实现了相与相之间的电气隔离。

图1 五相开绕组永磁同步电机拓扑结构 Fig.1 Topological Structure Diagram of Five-phase Open-winding Permanent Magnet Fault-tolerant Motor

为方便对故障情况进行分析，建立了相坐标系下的五相永磁同步电机的数学模型。同时，为简化分析过程，假设电机建模满足理想条件，即：

a）不考虑电机内电磁场的饱和，不计磁滞和涡流损耗；

b）忽略定子表面开槽的影响；

c）转子无阻尼电阻，忽略机械损耗。

基于上述假设，可得磁链方程：

式中n=a，b，c，d，e；in为n相绕组的电流；Ln为n相绕组的自感；ψmn为与n相绕组交链的永磁磁链，其中：

式中ψ1为永磁体磁链基波分量幅值；3ψ为永磁体磁链三次谐波分量幅值；kn在n=a时为0，在n=b时为1，在n=c时为2，在n=d时为3，在n=e时为4；Ls为定子电感的恒定值；Ls2为定子电感脉动量的峰值；θ为交轴偏离定子A相轴线的电角度，定义0时刻d1和d3轴与α轴重合，则有θ=ωt+π/2，ω为电角速度。

对于永磁同步电机，只有定子需要施加电压，故电压方程为

式中Rs为定子电阻。

根据虚位移法，电磁转矩与磁共能的关系满足：

式中p为电机的极对数；为磁共能。

磁共能的表达式为

将式（6）带入式（5），在不考虑磁阻转矩且互感为0的情况下可得转矩公式：

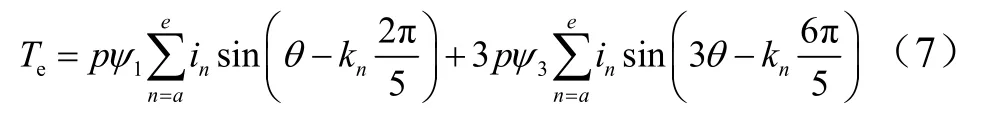
2 五相开绕组同步电机容错控制策略

2.1 容错电流

五相开绕组永磁容错电机由磁动势不变的约束条件可以得到：

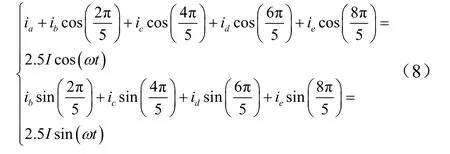
其中，各相电流的表达式为

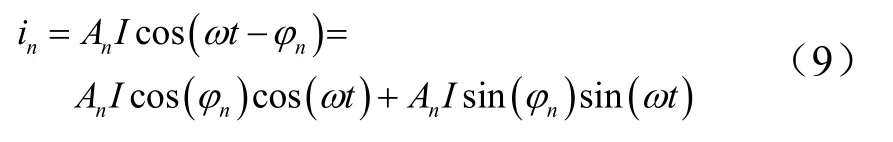
式中An为该相电流幅值相较于非故障时该相电流幅值的倍数；φn为该相电流相角。

An与φn两个变量将在下列推导中求得，令：

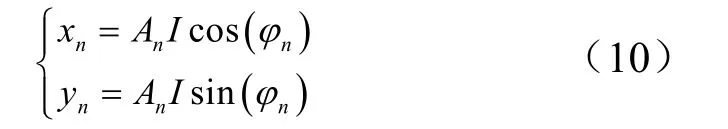
由式（8）至式（10）可得：

当一相发生开路故障时（以A相为例），则有xa=ya=0。此时，式（11）中的方程组只有 4个方程，但有8个未知量。为得到A相开路故障时的容错电流，需要额外的条件。

由式（8）可知，不考虑磁阻转矩的情况下，相转矩由相电流和与该相交链的永磁体磁链相互作用产生。磁动势不变的约束条件保证了故障后基波相电流与磁链基波分量的相互作用为恒值且与故障前一致。又由式（7）所示的相转矩公式可知，为实现转矩脉动为零，还需保证基波相电流与磁链三次谐波分量的相互作用为0，因此有：

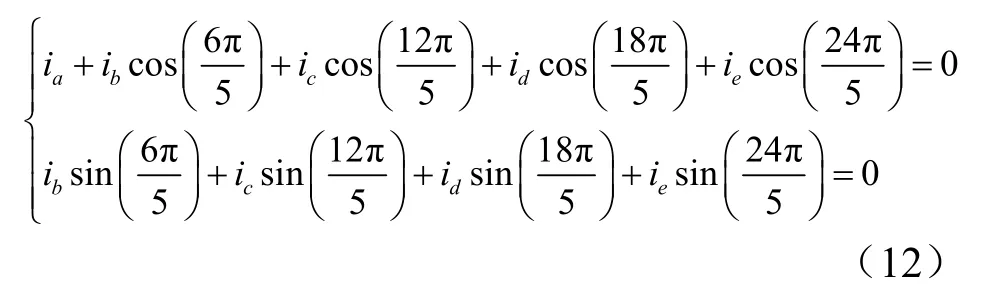
由式（9）、（10）和（12）可以得到4个方程组：

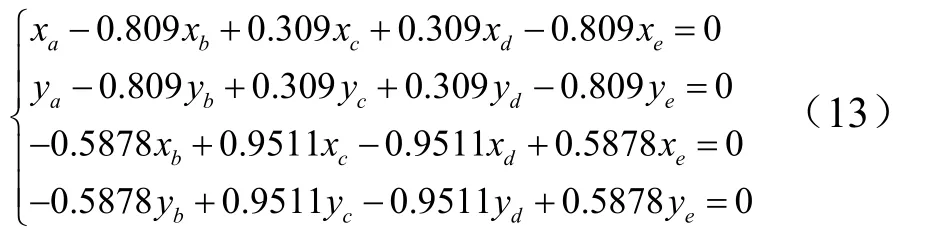
此时，A相发生开路故障时，式（11）和式（13）共包含8个方程可求解8个未知量，进而由8个未知量可以求解得到非故障相的基波电流：

同样，基于三次谐波电流在三次谐波空间产生恒定转矩、在基波空间不产生转矩的原则列写方程并求解，可以得到三次谐波电流：

由式（14）、（15）可知，基波空间和三次谐波空间互不产生影响，且三次谐波电流的相位与基波电流相位的 3倍有关，这使得通过注入谐波电流降低相电流峰值成为可能。

2.2 零序空间开环容错控制策略

五相开绕组永磁容错电机一相发生开路故障后，电机还有 4个自由度，在坐标变换后可以控制旋转坐标系下的 4个电流。由于本文采用的陶瓷轴承电机可以阻断零序电流的形成回路，零序电流可以开环，因此提出了一种零序空间开环的一相开路容错控制策略，其控制策略如图2所示。图2中，外环为转速环，实际转速与给定转速之间的偏差经过PI调节器后得到转矩Te的给定。自然坐标系下的五相反馈电流经过坐标变换，得到旋转坐标系下的id1、iq1、id3、iq3。采用id=0控制策略，即id1和id3的给定为0。与无故障情况下id1、iq1、id3、iq3和i05个电流环相比，图2中无零序电流环。

图2 零序空间开环控制策略 Fig.2 Block Diagram of the Zero-Sequence Space Open-Loop Fault-Tolerant Control Strategy

前向通道上由uα1、uβ1、uα3、uβ3得到ua、ub、uc、ud、ue时采用的 Clark-1需要在不同的开路故障时采用相对应的逆矩阵，由式（14）和式（15）可得A相开路时的Clark-1：

Park-1删除与零序相关的最后一行和最后一列，其他列不变，得到式（17）：

开路相的电流始终为零，在坐标变换过程中不影响d-q轴的电流，因此无论哪一相开路，反馈通道上的降阶解耦矩阵中只需在无故障的解耦矩阵基础上删除与零序空间相关的最后一行，无需删除故障相所在的列，即降阶解耦矩阵的前4行与故障前一致，如式（18）所示。因此图2所示的零序空间开环容错控制策略框图只需改变Clark-1即可适用于任意一相故障。

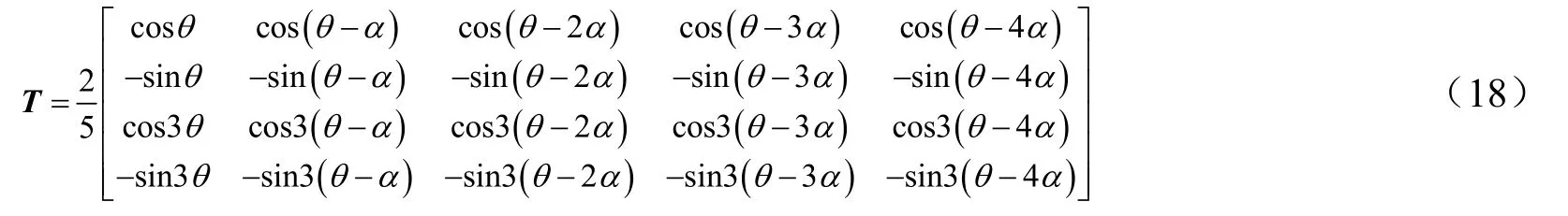
2.3 三次谐波电流注入

由式（14）和式（15）可以得到基波电流和三次谐波电流存在以下关系：

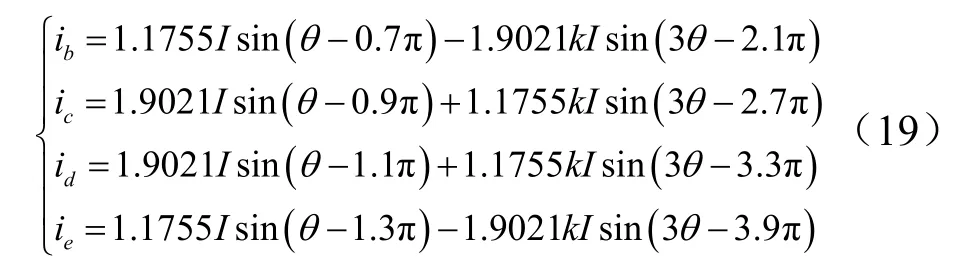
式中k为三次谐波电流的注入率。

由式（19）可得ib与ie的三次谐波电流与ic与id的三次谐波电流符号相反，因此必然存在两相电流幅值减小的同时另外两相电流幅值增加的情况。由式（7）可得正常工作时的相电流峰值I与转矩Te的关系为

当k＞0时三次谐波电流产生的转矩与基波电流的转矩同号，ib与ie的电流幅值增加，ic与id的电流幅值减小。由于ic与id的基波幅值比ib与ie大，因此选择合适的注入率可以降低相电流幅值的最大值。

本文所采用的电机共有 6对极，其基波磁链Ψm1为 0.0908 Wb，三次谐波磁链Ψm3为 0.0036 Wb。当Te=1时，根据式（19）和式（20），采用遍历寻优的方法可以得到相电流幅值随注入率的变化如图3所示。由图3可以得到，当三次谐波电流注入率为0.249时，相电流峰值的最大值最小，此时四相电流峰值相等，相较于未注入前，相电流峰值降低了15.8%。

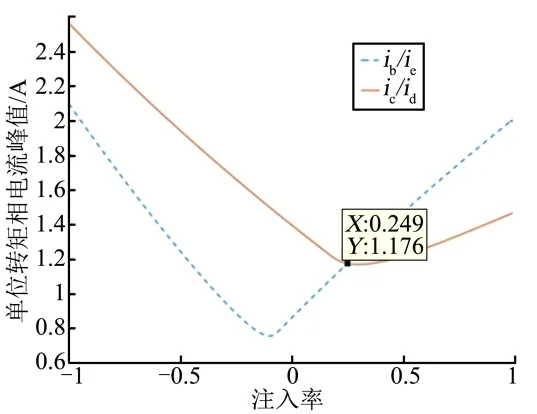
图3 电流峰值随注入率k的变化规律 Fig.3 The Diagram of the Variation of Current Peak Value with Injection Rate k

图4为不注入三次谐波电流的相电流波形，图5为以0.249为注入率注入三次谐波电流的相电流波形。

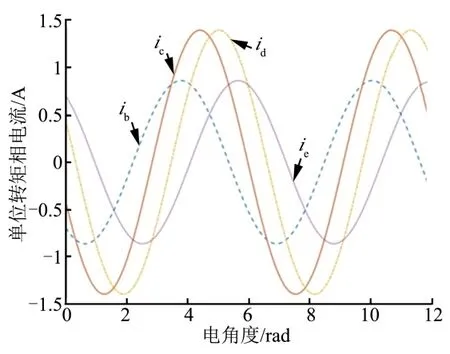
图4 不注入三次谐波电流的容错电流波形 Fig.4 Waveform Diagram of Phase Current without Injection of Third Harmonic Current

图5 注入率为0.249的容错电流波形 Fig.5 Waveform Diagram of Phase Current with Injection Rate of 0.249

3 仿真分析

3.1 仿真平台及参数

搭建仿真模型，其具体参数设置如表1所示，电机额定功率为20 kW，将电机中A相电流于电机模型中设置为0用于模拟A相绕组开路，并分别对第2节中提出的零序电流开环容错控制策略和使得相电流幅值最小的三次谐波电流注入率进行仿真验证。

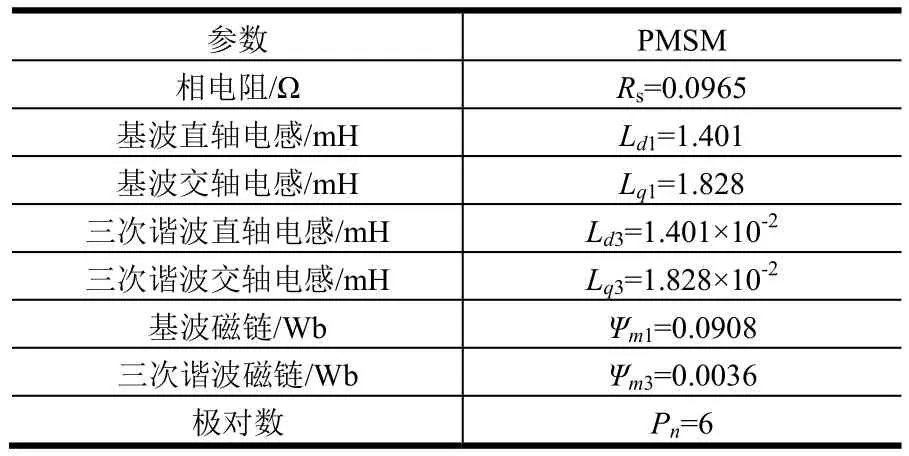
表1 仿真参数 Tab.1 Simulation Parameters

3.2 仿真结果及分析

仿真的工况为：给定转速 1500 r/min，负载转矩30 N·m，开关频率 10 kHz。图6为无故障时的转矩波形，转矩脉动的峰值约为1 N·m。

图6 无故障情况下输出转矩 Fig.6 Torque without Failure

图7为相同工况下，五相开绕组永磁容错电机A相开路时采用零序电流开环容错控制策略得到的转矩波形，转矩脉动与无故障情况下一致。图8为非故障相的容错电流波形，与图4所示的理论容错电流幅值和相位关系一致。

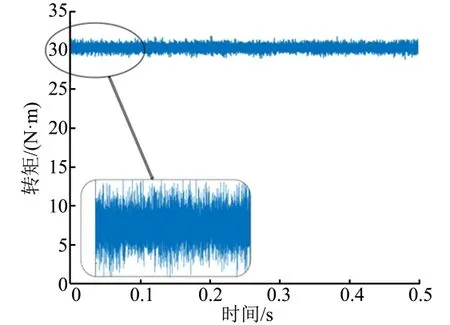
图7 A相开路采用零序电流开环容错控制策略时的输出转矩 Fig.7 Output Torque when the Zero Sequence Space Open Loop Fault-Tolerant Control Strategy is Adopted after the Phase A is Open

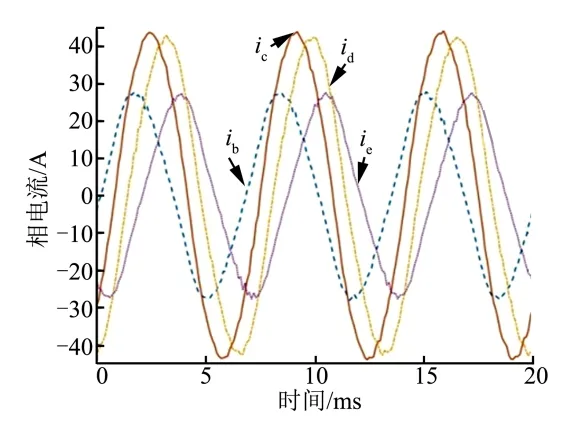
图8 A相开路采用零序电流开环容错控制策略时的非故障 相容错电流波形 Fig.8 Fault-tolerant Current Waveformwhen the Zero Sequence Space Open Loop Fault-Tolerant Control Strategy is Adopted after the Phase A is Open

图9为相同工况下，以0.249为注入率注入三次谐波得到的非故障相容错电流波形，与2.3节图5所示的理论相电流波形幅值和相位关系一致。由于注入的三次谐波电流会产生恒定的转矩，从而降低相同转矩下的基波电流峰值，因此相较于图8，相电流幅值降低了18.6%。

图9 注入率为0.249时的非故障相容错电流波形 Fig.9 Fault-tolerant Current Waveform when the Injection Rate is 0.249

4 结 论

针对采用陶瓷轴承的五相开绕组永磁容错电机提出了一种零序电流开环的开路故障容错控制策略，并通过仿真验证了该策略的有效性。具体结论如下：

a）采用陶瓷轴承的五相开绕组永磁容错电机无相电流和为零的约束，采用零序电流开环容错控制策略可以在一相开路故障下得到与无故障情况下相同的转矩脉动。

b）由于故障相的相电流始终为零，因此反馈通路上的降阶解耦矩阵只需在原矩阵的基础上删除与零序电流相关的最后一行，无需删除与故障相有关的列，因此降阶解耦矩阵不会随故障位置的不同而改变。

c）采用零序电流开环容错控制策略可以实现三次谐波电流的注入，其中注入率为0.249时，相电流幅值最低，相较于无注入情况降低了18.6%。