再入飞行器禁飞区规避近似解析制导方法

赵亮博，朱广生，庄 凌，宋加洪，卢宝刚

（1.北京航天长征飞行器研究所，北京，100076；2.中国运载火箭技术研究院，北京，100076）

0 引 言

再入飞行器的机动制导问题，一直是再入飞行器制导控制领域的研究热点[1～3]。飞行器再入制导过程具有非线性、时变性和不确定性等特点，其飞行路径除了需要满足过载、动压、热流率约束外，还需要满足由自然、军事等因素造成的禁飞区约束。

禁飞区约束是一种复杂的路径约束，现有禁飞区规避方法主要集中在离线最优轨迹解算中，如经典的数值求解方法伪谱法[4]，通过不同配点和多项式插值方式实现全局轨迹的优化求解。但是离线求解方法解算效率低，无法满足实时制导需求。随着探测技术发展，对禁飞区域的实时或近似实时探测成为可能，因此需要研究实现禁飞区在线规避的制导算法。文献[5]提出了一种考虑禁飞区的预测校正制导方法，利用航向角误差走廊的形式控制飞行器的侧向运动，当禁飞区等约束急剧变化时预测校正的制导方法易产生性能退化。文献[6]利用一种基于三触角预测方法的侧滑角瞬变策略，实现了禁飞区的规避，但机动轨迹的生成依赖于飞行器动力学方程积分而来的3个“触角”，计算代价大。

基于Dubins曲线的路径规划方法在机器人、无人机的轨迹规划中得到了广泛应用[7～9]。文献[10]第1次提出Dubins路径的概念，在转弯半径对车辆运动影响的分析上，设计了满足约束条件的最短路径并进行了理论证明，即满足曲率限制的最短曲线由圆弧与直线构成。文献[11]设计了基于 Dubins曲线的高超声速飞行器离线路径规划方法，但未结合具体的飞行器转弯能力和终端约束进行分析。

本文在对再入飞行器转弯能力分析的基础上，得出飞行器转弯半径和倾侧角的近似解析关系，结合Dubins曲线的路径规划方法生成禁飞区规避的制导策略。同时为修正规避引起的终端误差，建立基于能量运动模型来解析预测航程，通过割线法对倾侧角指令进行迭代修正，实现航程校正控制。通过速度倾角的反馈控制设计，满足终端高度约束。最后基于CAV-H的数学模型仿真验证了该算法在禁飞区绕飞规避的有效性，满足终端约束条件且计算效率高、实时性好。

1 飞行器运动建模

1.1 再入运动方程

本文研究的飞行器采用无动力滑翔的方式再入，采取倾斜转弯（Bank To Turn，BTT）的机动策略。为研究飞行器在大气层内的运动规律、分析飞行器转弯能力、设计制导策略，在不考虑地球自转影响的情况下，建立飞行器再入运动方程组为

式中r,λ,φ,V,θ,ψ分别为地心距、经度、纬度、速度、速度倾角和航向角；σ为倾侧角；g为重力加速度；L，D分别为气动升力和阻力，且：

式中ρ为大气密度；Sref为参考面积；CL，CD分别为升力系数和阻力系数。

由于飞行结束时间不确定，给航程解析预测带来了困难。为此，定义如下形式的无量纲变量e能量：

式中为无量纲的地心距，无量纲化参数为地球半径R0；为无量纲速度，无量纲化参数为，g0为海平面重力加速度。为解析预测航程需要，建立如下归一化的基于能量的运动方程：

式中为无量纲阻力加速度，无量纲系数为g0。

1.2 再入约束建模

本文考虑的终端约束有高度约束、速度约束及终端位置约束，以能量为自变量时表达式如下：

式中ef,rf,Vf,λf,φf分别为以能量为自变量描述的终端能量、地心距、速度、经度和纬度。

由于地理、军事等因素会造成飞行器不能在某些区域飞行，即禁飞区，通常用无限高圆柱表示。用经纬度及禁飞区半径rN描述禁飞区如下：

式中λz,φz分别为禁飞区中心的经度和纬度。

函数s((λz,φz), (λ,φ) )表示两点间的大地线长度：

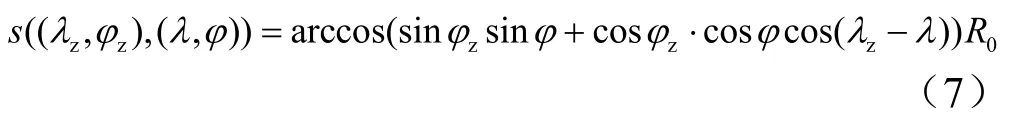
2 制导策略

本文将制导策略分为禁飞区规避制导和完成规避后的校正策略两部分设计，具体算法流程如图1所示。

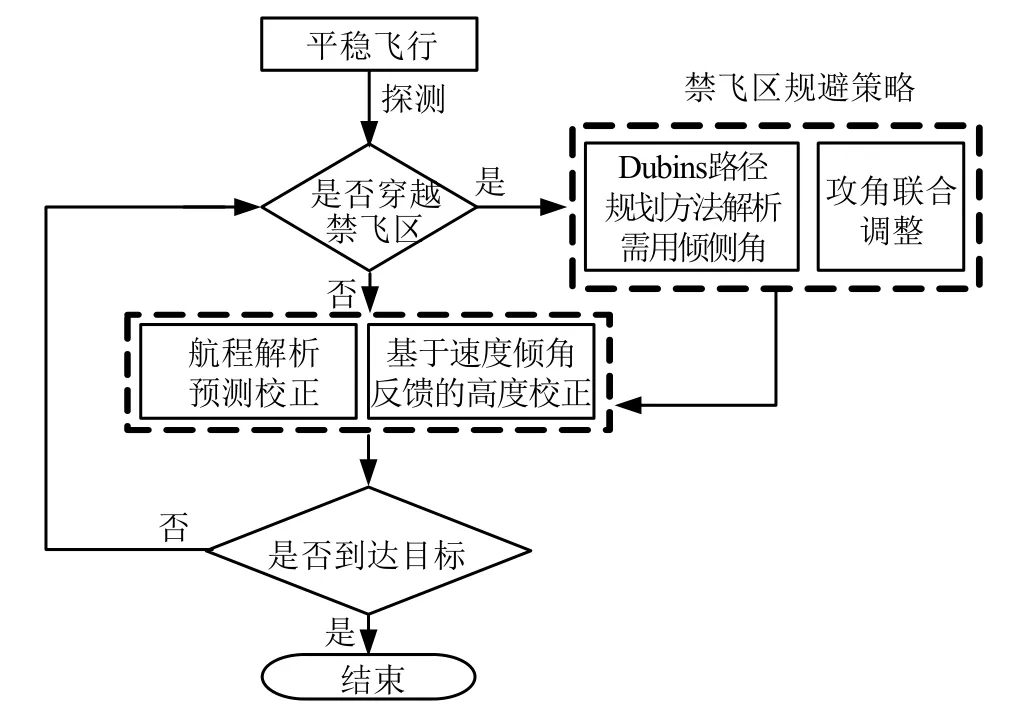
图1 制导算法流程 Fig.1 Guidance Algorithm Flow

2.1 转弯能力分析

为设计禁飞区规避策略，需要对飞行器的转弯能力进行分析。对于采用BTT机动方式的飞行器，通过倾斜升力面的方式使升力产生侧向分量，提供转弯的需用向心力。

假设转弯过程为无侧滑的平衡飞行状态，即转弯过程中速度倾角近似为零：

转弯过程中的需用向心力由升力的分量Lsinσ提供，定义转弯半径为rz，可得：

联立式（8）、式（9）可得：

在水平转动平面内忽略离心力项，可得机动转弯半径的近似解析解：

因此，一定转弯半径rz下倾侧角σ的近似解析解：

为验证该公式，针对CAV-H飞行器在高度50 km、速度 5000 m/s和高度 55 km、速度 5500 m/s两组不同的工况进行仿真验证。

图2 工况一：高度 50 km，速度 5000 m/s Fig.2 Condition 1: height 50 km, velocity 5000 m/s

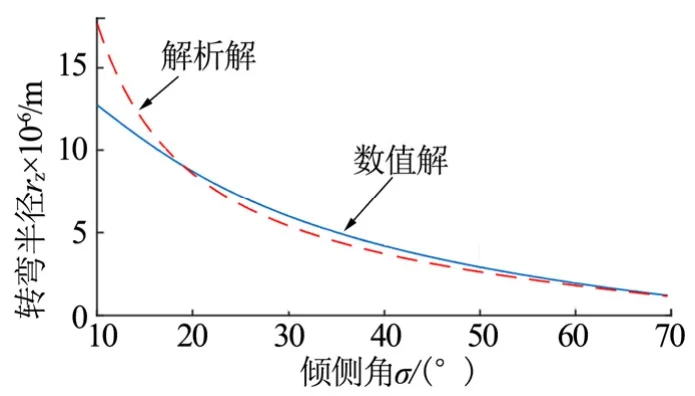
图3 工况二：高度 55 km，速度 5500 m/s Fig.3 Condition 2: height 55 km, velocity 5500 m/s

该公式建立在平衡滑翔飞行的基础上，可以用作该状态下倾侧角和转弯半径的解析计算。从图2、图3中可以看出，当倾侧角大于25°时解析解和数值解误差较小，式（12）可为机动策略的选取提供依据。

此外，在实际转弯过程中由于升力在铅垂方向上的分量减小，如果不对攻角加以调节会引起飞行高度的下降。为方便设计参考，本文给出了无攻角联合调节时机动转弯引起的高度损失近似估算公式。

假设转弯前后飞行器的高度分别为h1,h2，大气密度分别为ρ1,ρ2，根据大气密度的近似估算公式可得：

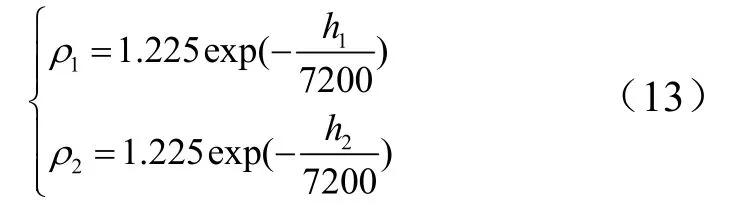
转弯后为维持平衡飞行，推导出大气密度变化规律：

因此，高度变化量Δh和倾侧角间的近似解析关系为

该关系式可用做转弯引起高度损失的近似估算，对机动策略的选取具有参考意义。

2.2 基于Dubins曲线的禁飞区规避策略

飞行器由起始状态调整至目标状态所经过的路径是经计算选择的一个起始转向圆rz1与一个目标转向圆rz2之间通过合适的公切线相连得到的有向曲线，此有向曲线即是一条Dubins路径[10]，如图4所示。

图4 Dubins路径 Fig.4 Dubins Path

依据 Dubins曲线的组成原理确定本文的绕飞策略，其中需要求解的变量包括 2次转弯的转弯半径rz1,rz2及转弯角度θ1,θ2。同时，针对转弯过程中可能出现的高度损失，采用攻角和倾侧角联合调整的方法设计攻角大小。具体的规避流程如图5所示。

图5 基于Dubins曲线的规避流程 Fig.5 Avoiding Process Based on Dubins Curve

假设对禁飞区的探测距离为rdet，即在距离rdet时发现禁飞区。对于半径为rz大小的禁飞区，Dubins曲线起始圆的最小转弯半径rz1计算公式为

由式（16）可得，飞行器探测到禁飞区的时机越早、探测距离越远，需用机动转弯半径越大。联合式（12）与式（16）即可求出规避禁飞区的需用倾侧角σrz1。同时，根据相切点位置通过解析几何的方式可求出转弯角度1θ的大小。

通过目标圆的半径rz2选取对应倾侧角σrz2大小时需进行判断，假设当前飞行状态下转弯半径rz对应的倾侧角为σrz，通过式（23）得出的倾侧角大小为σcmd，则：

然后，通过判断航向角误差是否为0，即飞行器是否瞄准目标点，作为转弯结束的标志并进入校正环节，不再计算目标圆旋转角度2θ。

由式（15）可得，转弯时如果不对总升力进行调节，会引起飞行器的高度损失。本文通过联合调整攻角的方式来调整升力，补偿高度损失，近似平衡滑翔飞行时存在如下关系式：

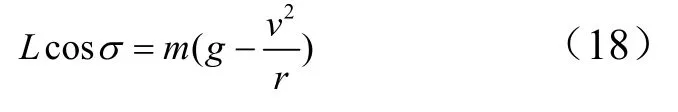
可求得该飞行条件下的需用升力，通过气动反插值的方式求出需用攻角。

需要指出的是，当倾侧过大时为了补偿高度损失所需用的攻角较大，大攻角飞行时升阻比低会产生较大的速度损失。因此需设定合理的攻角联合调节范围［αlow,αmax］，针对CAV-H飞行器，本文选取的攻角调节区间为[8°，15°]。

2.3 航程解析预测校正控制

完成禁飞区规避后，飞行器高度和速度会产生相应的损失。为满足终端约束，需对航程及高度进行校正。本文通过倾侧角大小的调节，实现航程的校正。根据文献[12]的推导，基于能量的运动模型进行航程预测：

式中(ef)为从能量e到能量ef的归一化预测航程，归一化变量为地球半径R0。此时，预测航程和待飞航程的差值：

式中s为当前真实的待飞航程，可通过式（7）并结合当前点和终点的经纬度坐标求出。

通过调节倾侧角大小的方式实现对航程的在线校正，采用割线法不断迭代倾侧角大小：

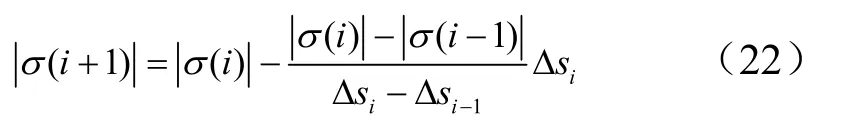
2.4 终端高度控制

在再入飞行的大部分时间内，飞行攻角处于最大升阻比大小附近，通常采用攻角剖面的形式设计攻角大小，同时实现满足过程约束：

式中αm为较大攻角，使飞行器在初始阶段快速达到平衡滑翔的飞行状态；αL/D为最大升阻比攻角；VL/D和Vm为设计变量，实现对不同飞行阶段攻角大小的控制。

在飞行末段，为实现满足终端高度约束，不采用攻角剖面的形式。本文通过设计一种速度倾角反馈控制的策略调整攻角大小，期望速度倾角dθ设计为

设计线性反馈跟踪控制律：

联合式（1）可求得需用升力Lc：

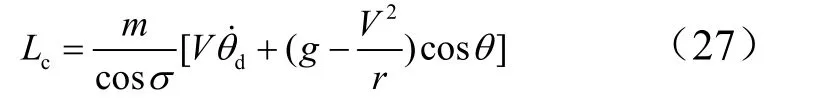
同样，通过气动反插值的方式求出需用攻角：

对于航向的控制采用传统航向角误差走廊的形式实现，在此不做赘述。

3 仿真结果及分析

本文采用CAV-H飞行器的数学模型，进行仿真验证[14]，仿真初始及终端条件见表1。

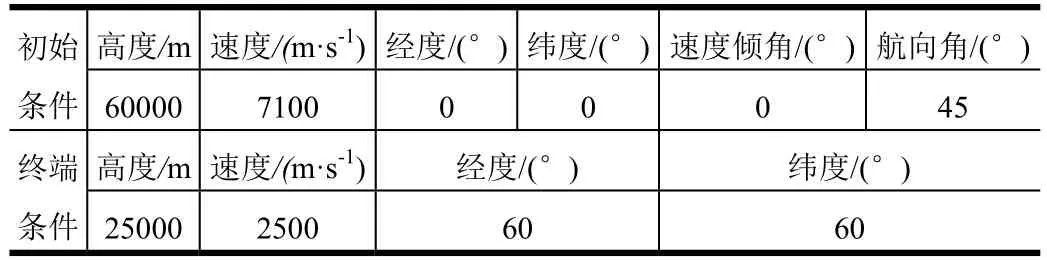
表1 初始条件及终端条件 Tab.1 Initial Conditions and Terminal Conditions

假设飞行器探测距离为2000 km，探测到禁飞区中心经纬度为（30°，40°），禁飞区半径500 km。通过Dubins曲线的路径规划策略生成的起始圆起点经纬度（20.92°，23.71°），旋转角度θ1=28.07°，旋转半径rz1=3750 km，对应的近似解析倾侧角大小σrz1=46.99°；校正制导起点经纬度（50.34°，48.80°），具体仿真结果如图6～9所示。

图6 CAV-H规避禁飞区三维轨迹 Fig.6 Three-dimensional Trajectory Formed by CAV-H Avoiding the No-fly Zone

图7 CAV-H规避禁飞区星下点轨迹 Fig.7 Subsatellite Track Formed by CAV-H Avoiding the No-fly Zone

由图6、图7可得，飞行器能够有效实现禁飞区的规避，其终端脱靶量611.80 m，精度较高。

图8为飞行器的高度、速度曲线，终端高度误差15.42 m、速度误差14.03 m/s，均在合理偏差范围内，且高度及速变化平稳。

图8 高度和速度曲线 Fig.8 Height and Velocity Curve

图9为飞行器的攻角和倾侧角曲线。

图9 攻角和倾侧角曲线 Fig.9 Angle of Attack and Bank Curve

飞行器分别在519.8 s和809.8 s进行了机动转弯，实现了禁飞区的绕飞规避和目标的重新瞄准。在接近目标时，攻角逐渐增大校正终端高度，同时连续调整倾侧符号修正航向误差。

4 结 论

本文提出了一种基于近似解析解的制导方法，能够有效实现禁飞区的绕飞规避，同时满足终端航程及高度约束，该方法具有以下特点：

a）对飞行器的转弯能力进行了分析，得到了机动转弯半径和倾侧角的近似解析关系；

b）结合 Dubins曲线的路径规划方法设计规避策略，结构简单、效率高；

c）通过对航程的解析预测和速度倾角的反馈设计，实现了终端航程及高度的控制，计算效率高、误差小。

通过数学仿真验证了算法的有效性，得到的近似解析关系对机动制导算法的设计也具有参考价值，工程实用性强。