正交多载波降噪差分混沌键控通信系统

贺利芳 吴雪霜 张天骐

(重庆邮电大学通信与信息工程学院 重庆 400065)

1 引言

混沌信号的研究始于上个世纪90年代，混沌是确定系统受到内部随机性影响后，对外表现出的一种无规则的有序行为，这种有周期的无序行为具有以下两个重要特征：(1)当初始值被确定，运动轨迹也将被确定；(2)在初始值未知的情况下，运动轨迹也未知[1]。这种对初始条件的极度敏感性，使得不同初始状态下的混沌信号在运动轨迹上有着巨大的差异，在长时间内难以被预测和捕捉到，因此在通信与信息领域展现出了诱人的应用前景和重大的实用价值[2,3]。

传统差分混沌移位键控(Differential Chaos Shift Keying, DCSK)通信系统作为扩频通信方案的重要代表，具有误码性能好和抗干扰能力强的优点，但存在传输速率低的缺点。为提升系统的传输速率，众多学者对DCSK提出改进。然而，传统的以DCSK为基础改进的多用户DCSK系统往往需要使用大量的延时单元和开关，极大程度上增加了系统的硬件复杂度[4-10]。为减少传统多用户DCSK通信系统中延迟电路和开关的使用，Kaddoum等人在文献[11]中提出了一种多载波差分混沌移位键控(MultiCarrier Differential Chaos Shift Keying,MC-DCSK)系统，使用多个不同中心频率的载波信号发送低速子数据流，分散了接收端由衰落或干扰引起的错误。文献[12]将多载波调制(MultiCarrier Modulation, MCM)和Hilbert变换技术与DCSK系统相结合，并利用凸优算法寻找最佳参数因子用于优化系统误码性能。文献[13]在MC-DCSK系统上做出改进，采用正交调制(Quadrature Modulation, QM)技术在同一频率的正、余弦载波上发送信息比特，将传输速率和频带利用率提高为MC-DCSK系统的两倍。文献[14]提出了一种基于子载波分配的多载波差分混沌键控降噪(MultiCarrier Differential Chaos Shift Keying system with Subcarriers Allocation for noise reduction, SA-MCDCSK)系统，使用N个载波重复发送参考信号用于在接收端进行平均操作，M-N个载波发送信息信号，这种方法虽然提高了误码性能和传输速率，但同时也牺牲了频带资源。

相比于传统多用户DCSK系统，本文所提正交多载波降噪差分混沌移位键控(Quadrature Multi-Carrier Noise Reduction Differential Chaos Shift Keying, QMC-NR-DCSK)系统采用多个载波传输低速并行的数据比特流，减小了因信道时延扩展引起的信号间干扰，有良好的抗多径干扰特性，且减少了开关和延时电路的使用，降低了系统的硬件复杂度。此外，在系统的接收端，采用滑动平均滤波器对参考信号和信息信号进行平均操作，降低了噪声的干扰，提升了系统误码性能。因此QMC-NRDCSK系统具有传输速率、带宽效率和误码性能好的优点。

2 QMC-NR-DCSK原理

Walsh码是一种同步正交码，具有良好的自相关特性和处处为零的互相关特性，常用于多用户通信系统中用于消除用户间干扰。Hadamard矩阵是一种元素为1和-1构成的正交矩阵，矩阵的任意两行或者两列都是完全正交的，且其阶数是4的倍数，等于任意一行(列)的所有元素的平方和。 2n阶Walsh码构造方式简单，可直接由多阶Hadamard矩阵展开取行得到， 2n阶Walsh码生成方式为[15]

其中, n =0,1,··· , W20=[1]。矩阵的每一行代表一个长度为P 的Walsh码，P =2n。

串并转换将需要传输的高速比特流数据转化为4(M-1)个低速并行的数据子流，其中bj={+1,-1}(j =1,2,···,4M -4), Tb和 Tc分别代表比特周期和码片周期，为便于后文理论比特误码率(Bit Error Rate, BER)公式的推导，取Tc=1。 将Tb和 Tc的比值定义为扩频因子β (β =Tb/Tc)。

图1为QMC-NR-DCSK系统的发送机结构。首先采用混沌信号发生器产生一段长度为β /P的混沌序列x「i/P⏋,k(i=1,2,···,β), 「·⏋表示向上取整。2阶Logistic映射工作在纯混沌状态，且利用该映射产生的混沌序列具有良好的数学统计特性，因此在本文中利用该映射产生混沌序列，2阶Logistic映射方程如式(2)[16]

图1 QMC-NR-DCSK系统发送机结构

最后，参考信号x (t) 在中心频率为f1的预定义载波上进行发送， dm1(t) 是 b4m-7和b4m-6分别调制x(t) 和y (t)后得到的扩频信号，在中心频率为fm(m=2,3,···,M)的余弦子载波上进行发送，与此同时，b4m-5和 b4m-4分 别调制x (t)和 y (t)，得到扩频信号dm2(t)在 中心频率为fm的正弦子载波上进行发送。dm1(t) 和 dm2(t)的表达式如式(6)和式(7)所示

x(t) , dm1(t) , dm2(t) 和 s (t)的带宽均满足奈奎斯特(Nyquist)定理，将带宽定义为B =(1+α)Tc，其中 α为升余弦滚降滤波器的滚降系数[17]，图2为s(t)的功率谱密度，为避免频带间干扰，在每个频带之间设置一段保护带宽Bs(Bs=B)。

由式(8)计算出QMC-NR-DCSK系统的平均比特能量Eb

图3(a)为QMC-NR-DCSK系统的接收机结构图。假设接收端子载波同步，且忽略不计发送端和接收端中带限信号和边带信号的影响。以解调第k帧中中心频率为 fm的正、余弦载波上传输的信息比特为例，解调过程可分以下3步进行

步骤 1 接收信号r (t) 与 载波c os(2πf1t+φ1)相乘，再经匹配滤波器后恢复出g (t); r (t)与相应的载波cos(2πfmt+φm) 和sin(2πfmt+φm)相乘，后再经过匹配滤波器恢复出gm1(t)和 gm2(t)。

步骤 2 将恢复出的信号g (t), gm1(t), gm2(t)进行采样，假设采样为理想采样，采样间隔设为iTc(i=1,2,···,β)。然后，将经采样后得到的离散信号都送入窗口为P的滑动平均滤波器进行平均操作，得到平均后的信号 hi,k,,，平均后的信号长度变为β /P 。以图3(b)中平均gi,k的滑动平均滤波器为例简述滑动平均滤波器的原理，其中，gi,k是 g (t)经采样后得到的离散信号，其原理可描述为：从送入信号的第1个码片开始，滑动平均滤波器将根据窗口大小每次对P个码片进行加和平均，直至平均完β 个码片。

步骤 3 平均后的信号分别与相应的参考信号进行相关运算，相关运算值表达式为

然后再经串并转换恢复出传输的信息比特。

3 传输速率、能量效率和带宽效率分析

混沌数字通信中，传输速率(Transmission Rate, TR)表示为单位时间内传输的比特数；能量效率(Energy Efficiency, EE)由传输信息比特的能量和总的传输能量的比值表示；带宽效率(Bandwidth Efficiency, BE)由传输速率(TR)和占用信道带宽的比值表示。为凸显Q M C-N R-D C S K系统在传输速率、能量效率和带宽效率方面的优势，在表1中将QMC-NR-DCSK系统与其它几种多载波系统进行了对比。对比结果显示：QMC-NR-DCSK系统的能量效率都优于其它几种多载波系统的能量效率，带宽效率和传输速率明显优于MC-DCSK,SA-MCDCSK和QMC-DCSK系统，是MC-DCSK系 统的4倍，QMC-DCSK系统的2倍。

图3 QMC-NR-DCSK接收机结构图

表1 几种多载波系统间TR, EE和EB的对比

4 QMC-NR-DCSK性能分析

采用MCM技术传输的信号，在实际传输过程中会受到建筑物、树木等障碍物的影响，经反射、折射、直射和衍射等多条路径到达接收端，为使推导的结果更贴近于实际传输中的误码率，采用图4中多径RFC信道模型作为QMC-NR-DCSK的信道模型，其中， αl和 τl为第l条路径上的信道参数和信道延迟，L为信道衰落路径数。假设由多径时延引起的衰落是平坦衰落，此时满足条件Bs≪Bc, Ts≫στ(Bs为 信号带宽，Bc为 信道相关带宽，Ts为时延扩展，στ为信号的符号周期)。

经图4中信道传输后，接收信号r (t)可表示为

由于中心频率为 fm的正、余弦载波上传输的信息比特b4m-7, b4m-6, b4m-5和b4m-4的解调方式相同，故以推导 b4m-7的BER公式为例推导QMCNR-DCSK系统的BER公式。 Z4m-7的表达式可表示为

将式(17)和式(18)代入式(19)，计算出b4m-7的BER公式为

则QMC-NR-DCSK系统在多径RFC信道下的瞬时BER公式为

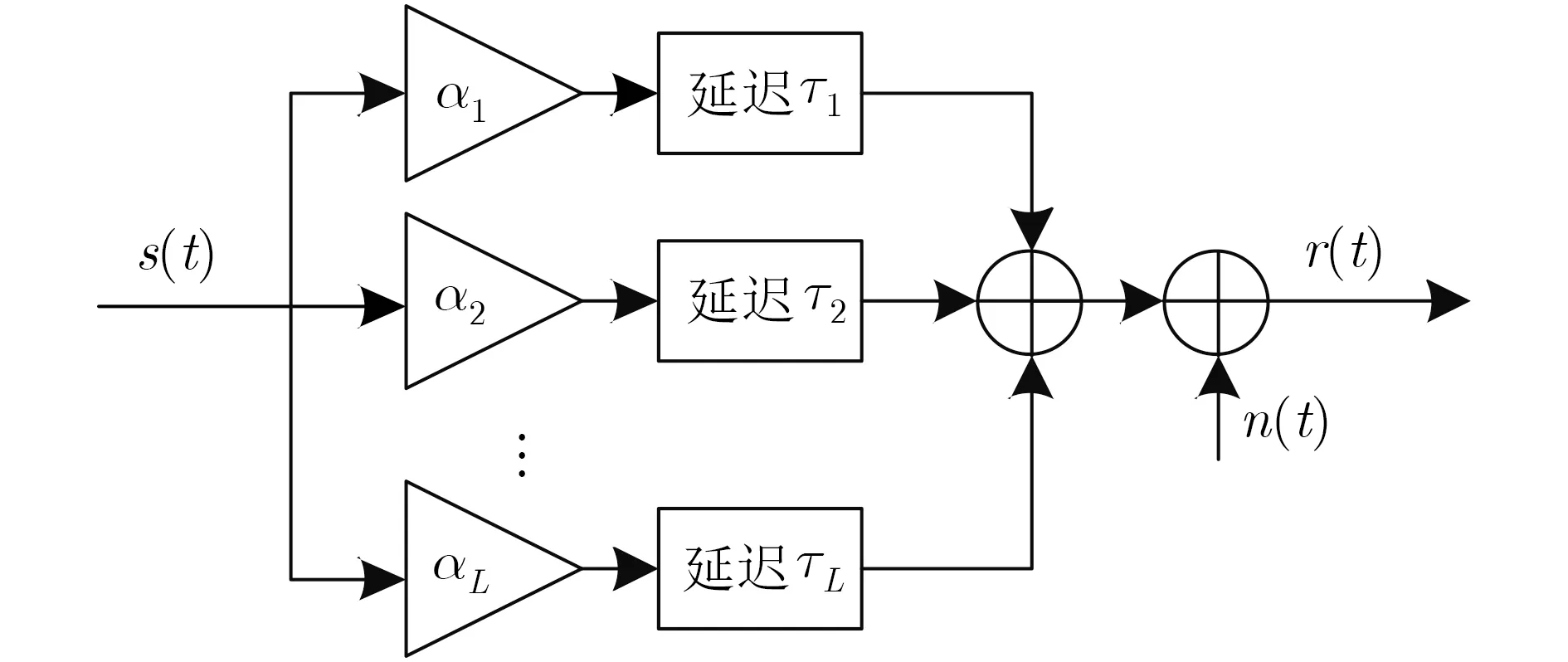
图4 多径RFC信道模型

对于多径RFC信道的L条独立且信道增益相同的路径，γb的概率密度函数表示为

由于信道参数是持续变化的，故QMC-NR-DCSK系统在多径RFC信道下的平均BER公式为

令α1=1,α2=···=αL=0 ， 有γb=Eb/N0，高斯信道下的BER公式表示为

5 系统仿真结果与分析

图5 为 [β,P,M]=[512,16,2],[512,16,8]时，QMC-NR-DCSK系统在两种不同信道下的BER随Eb/N0变化的曲线，其中，3径RFC信道的各项参数取值由表2中给出。图中仿真曲线和理论曲线没有较大的误差，重合良好，证明了BER公式推导的正确无误性。此外，由图中BER曲线的对比可以发现，系统BER随着M的增大而降低，验证了QMC-NR-DCSK系统采用大数量载波传输信息比特的可行性。

图5 两种不同信道下，M变化对BER的影响

表2 多径RFC信道参数取值表

图6为[β,P,M]=[512,16,8],[512,8,8],[512,2,8]时，QMC-NR-DCSK在两种不同信道下的BER随Eb/N0变化的曲线，3径RFC信道的各项参数取值由表2中给出。观察图中BER曲线可以发现，系统BER随着P的增加有明显的降低。在图6(a)中，P=16时的系统BER比 P =2时的系统BER降低了将近两个数量级；在图6(b)中， P=16时的系统BER比P=2时的系统BER降低了将近4 dB。可见采用滑动平均滤波器的降噪操作能有效降低系统的BER，在提升系统误码性能方面很有优势。此外，相比于M变化对系统BER的影响，P值变化对系统BER的影响更加明显。

图7中对比了 β 相同(β =256)，且占用频带数也相同的条件下，QMC-NR-DCSK与SA-MCDCSK,QMC-DCSK, MC-DCSK系统的BER曲线。图7(a)中，QMC-NR-DCSK系统的BER相比于MC-DCSK系统的BER降低了将近两个数量级，此时QMC-NR-DCSK系统的传输速率是MC-DCSK的4倍；观察图7(b)中BER曲线的对比结果，可以发现QMC-NR-DCSK系统的BER同样都优于其它几种系统。

图8为[ β,P,M]=[256,8,8]时，QMC-NR-DCSK系统在不同路径数下的BER曲线，L径RFC信道的各项参数由表2给出。从图8中仿真曲线可以观察到，系统BER随着L的增加而降低，且理论值和仿真值间的吻合性也越来越好。

图9给出了QMC-NR-DCSK([ β,P,M]=[512,16,8])系统BER随τ2变 化的曲线，系统BER随着τ2的增加而增加，但当 τ2的 取值为 P的倍数的时候，存在一个极小值，且这个极小值随着倍数的增加也是不断增大的，出现这种情况的原因是由于混沌序列的复制是将单个码片复制了P次，τ2延迟P次实际只造成了 接收端判决信号中一个码片的延迟。

6 结论

图6 两种不同信道下，P变化对BER的影响

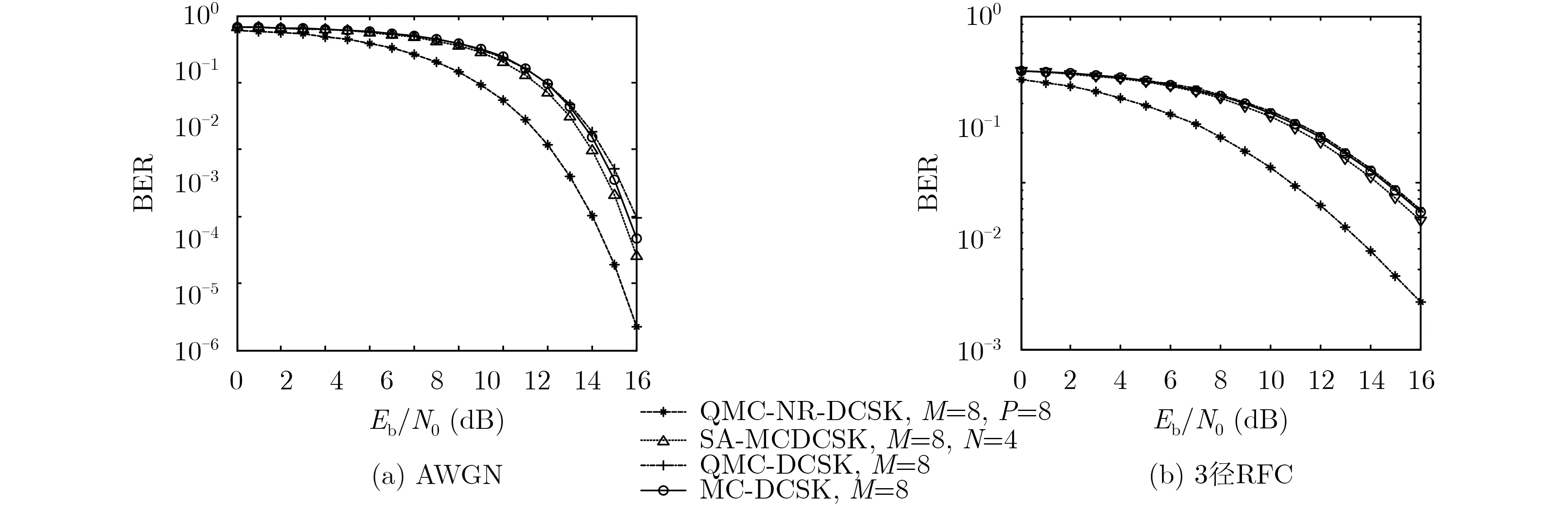
图7 两种不同信道下，不同系统误码性能对比图

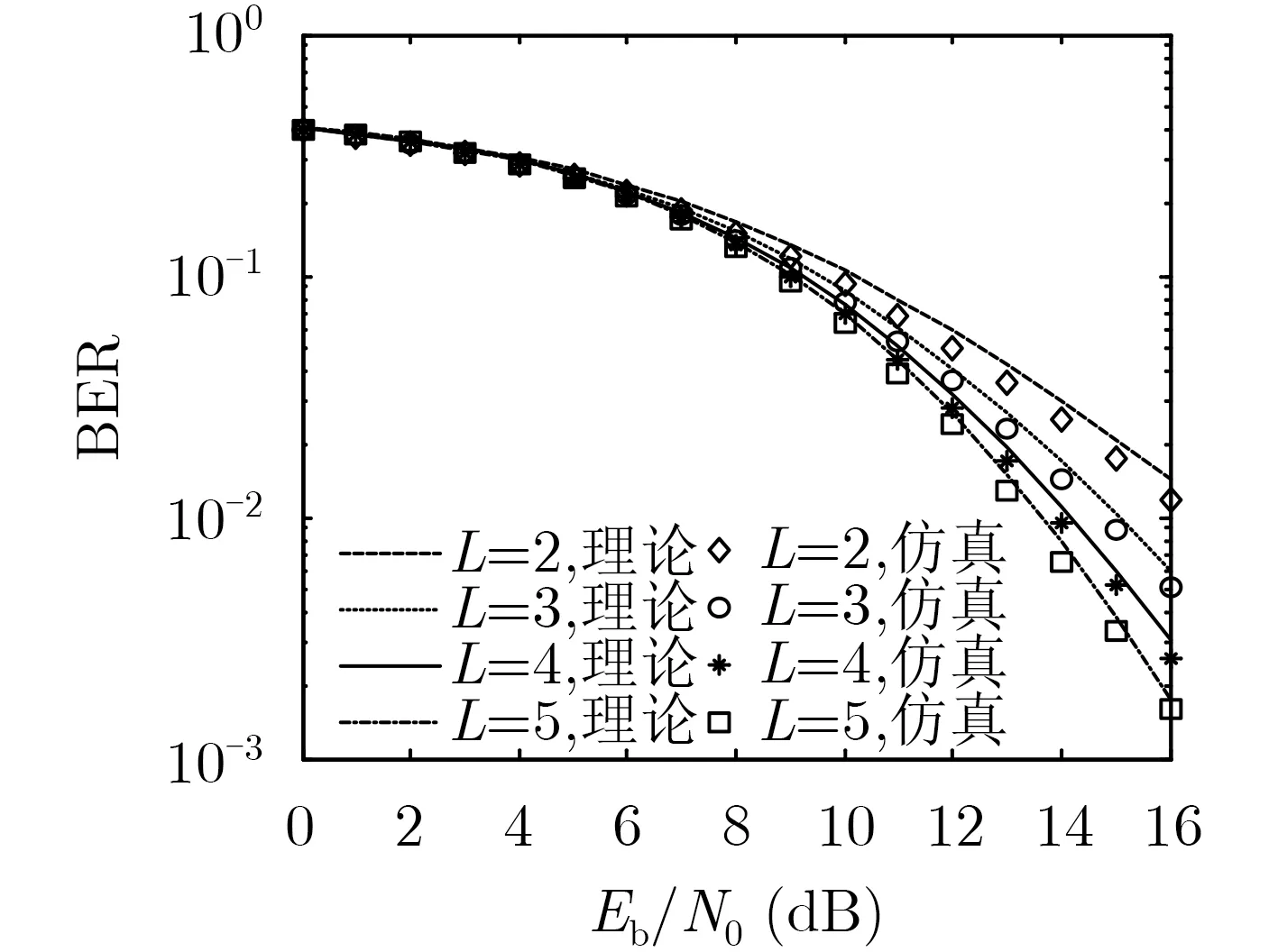
图8 BER随多径路数L变化的曲线

图9 BER随τ 2变化的曲线

本文提出的QMC-NR-DCSK系统结合QM技术和Hilbert变换，将传输速率提升为MC-DCSK系统传输速率的4倍，并结合滑动平均滤波器在降噪方面的优势，极大地改善了系统误码性能。通过仿真分析了平均次数、载波数量变化对系统BER的影响，增大平均次数和载波数可以提升系统误码性能，基于QMC-NR-DCSK系统BER随着载波数量的增大而降低这一特性，可采用大数量载波传输数据用于提升传输速率。此外将QMC-NR-DCSK系统与其它几种多载波系统进行对比，证实了QMCNR-DCSK系统性能的优良性。在现代无线通信系统中，常采用MCM, MIMO, OFDM(FDM), DSSS,FHSS, CDMA等对抗多径干扰，本文提出的QMCNR-DCSK系统满足了现代通信对系统高传输速率和良好误码性能的要求，为MCM技术在无线通信系统和无线广播中的应用提供了理论参考。