车联网中基于NOMA-MEC的卸载策略研究

张海波 刘香渝* 荆昆仑 刘开健 贺晓帆

①(重庆邮电大学通信与信息工程学院 重庆 400065)

②(移动通信技术重庆市重点实验室 重庆 400065)

③(武汉大学电子信息学院 武汉 430000)

1 引言

随着移动通信技术的发展以及移动终端设备的普及，新型车载终端应用对移动通信网络提出了更加严苛的要求。移动边缘计算(Mobile Edge Computing, MEC)技术的出现能够有效地解决这一挑战。MEC是一种新型通信架构，将具有计算、存储以及通信功能的服务平台安置在网络边缘，帮助移动终端用户将计算密集型、时延敏感型任务卸载到边缘节点进行处理[1,2]。MEC技术是第5代移动通信的一项重要技术，目前广泛应用于通信网络系统研究[3,4]。基于MEC的通信系统能够降低任务处理时间，同时减少移动终端设备的能耗以及传输成本[5-7]。在车联网场景下，新型的服务应用正在发展，如无人驾驶、超清视频、增强现实等[8]，MEC可以满足这些任务的高计算要求，而非正交多址(Non-Orthogonal Multiple Access, NOMA)技术的应用能够更进一步减少多任务卸载延迟的问题。

NOMA技术是第5代蜂窝网络的关键技术之一，通过为终端用户分配不同的功率，可以在同一频带上同时为多个用户提供服务，从而有效地提高频谱利用率[9]。NOMA已被视为在未来通信场景中增强系统容量的基本多址访问技术[10]。文献[11,12]将NOMA的上下行传输都应用于基于MEC的网络系统，并提出了基于Dinkelbach方法的迭代算法，最小化终端用户的卸载时延。文献[13]提出了两种用于V2X通信的中继辅助NOMA传输方案，有效地提高了用户的服务质量，减轻了流量拥塞并减少了任务延迟。

文献[14]研究了基于NOMA的卸载策略，但其中只包括关于正交多址接入(Orthogonal Multiple Access, OMA)或纯NOMA的卸载选择。文献[15]研究了NOMA技术在MEC下的卸载问题，利用混合型NOMA提高了卸载的信道利用率，但主要分析单个用户。文献[16]体现了在车联网中利用MEC可减少车辆任务卸载的时延和能耗，提高资源利用率。文献[17]讲述了NOMA在车联网中的可行性，可用于提高车联网的频谱效率。因此，在车联网下NOMA-MEC有效结合，能够进一步完善MEC技术在车联网中的应用，减少移动终端用户进行卸载的延迟和能耗；另外，现有关用户卸载的文献研究中，多是基于对能耗或者时延的单独优化。而在实际应用场景下，任务的卸载过程需要同时考虑到任务的时延敏感度和设备能耗的约束，而通过对混合NOMA-MEC卸载策略研究能够更加科学地完成任务卸载。

由此本文提出的混合NOMA-MEC卸载策略主要完成了以下工作：

(1) 将NOMA技术和基于MEC的车联网系统结合，构建了一个车联网通信模型，并利用NOMA的技术优势，更好地适应多用户应用场景，符合实际通信网络需求。

(2) 利用DQN合作博弈算法，通过竞争博弈确定信道选择，根据用户请求的任务属性以及卸载用户的数量，进行信道资源分配。通过合作博弈得到合作收益，以最大化用户效益。然后利用DQN，为用户选择最优的卸载策略。

(3) 设计了一种混合NOMA-MEC卸载选择机制，较全面地考虑到了目标优化函数的影响因子，从任务卸载的时延和能耗方面进行优化。主要是通过将部分用户按照传统OMA模式进行卸载，另一部分用户利用NOMA模式进行卸载传输来实现。

2 系统模型

在车联网下MEC通信网络系统中，车辆用户v ={1,2,···,V}通过同一个接入点与MEC服务器进行通信，并请求任务卸载至MEC服务器。该系统模型如图1所示，每个车辆用户卸载任务定义为Qv={Sv,Dv} ，其中Sv和 Dv分 别表示车辆用户v 需要卸载的任务大小和最大时延容忍度。

在NOMA-MEC的通信系统框架中，可以允许多个车辆用户在同一个时隙完成任务卸载。假设有两个车辆用户m和n同时请求任务卸载，若Dn≥Dm, m, n ∈{1,2,···,V}，那么在该模式下用户m和n可以同时在 Dm时隙内向MEC服务器进行卸载。车辆用户m和n的传输功率分别为和，在这需要指出如果用户m的信息在连续干扰消除(Successive Interference Cancelation, SIC)的第2阶段被解码，则用户m的性能与OMA相同，因此用户m的传输时延不会受到影响[18]。用户n的传输速率Rn在时隙Dm内为

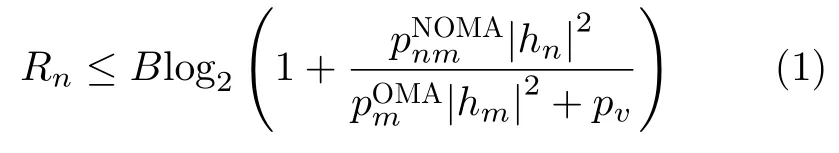
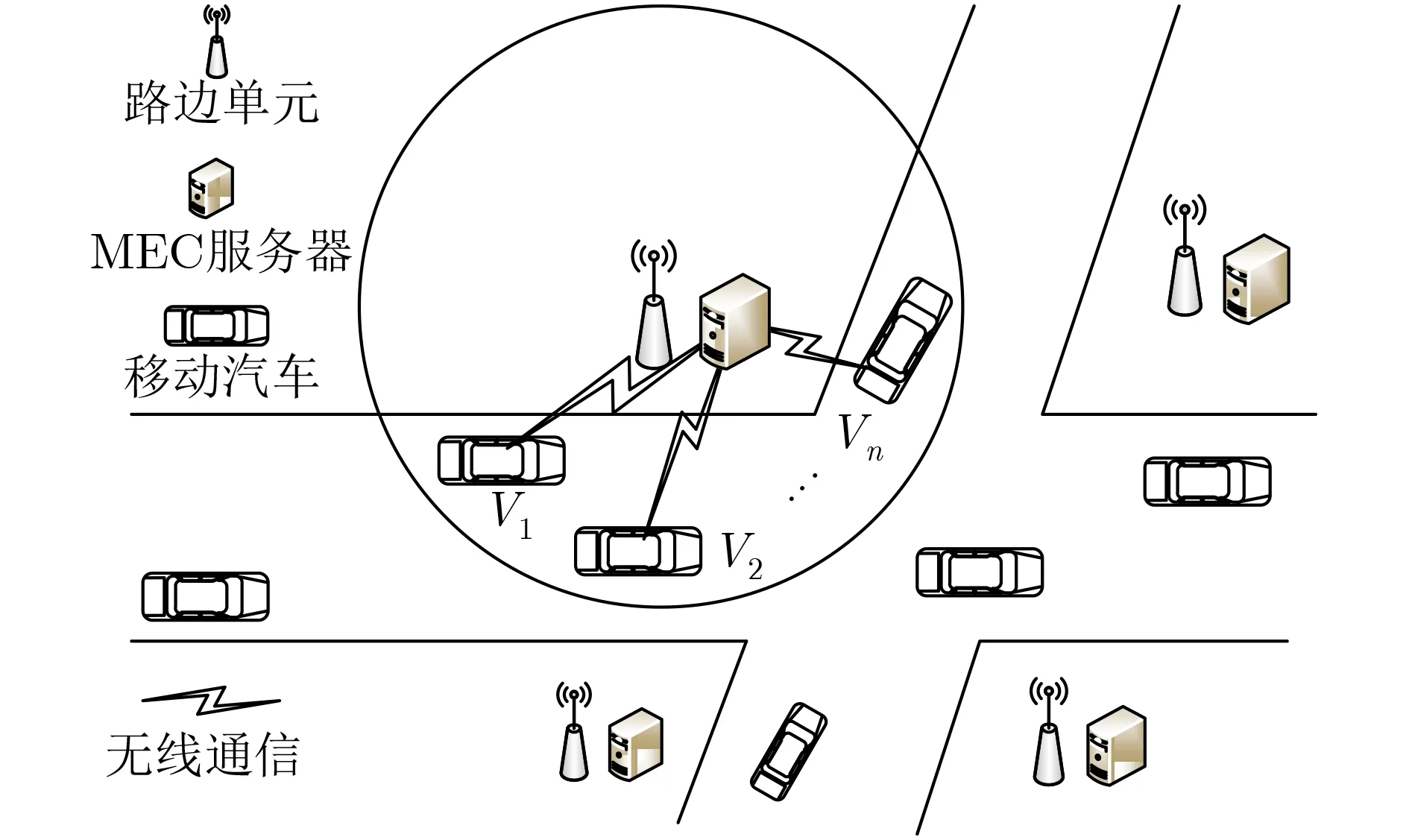
图1 系统模型图

3 混合NOMA-MEC卸载

混合NOMA-MEC卸载策略在最大限度满足任务的时延需求的同时，也能够减少任务卸载过程中的能量损耗。因此，混合NOMA-MEC卸载的优化目标主要是任务卸载的时延和能耗。具体来讲，在此过程中，优化目标是最小化总开销[19]，由式(4)表示

引理1在满足给定约束条件下，目标函数式(4)是一个非凸优化问题。

证明将优化目标函数式(4)转化为关于变量pNnmOMA和pNnnOMA的2元函数为

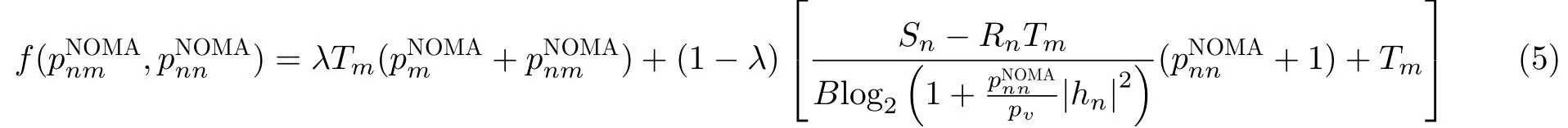
在上述目标函数里只含有两个变量因子，其余均默认为常量，因此简化为

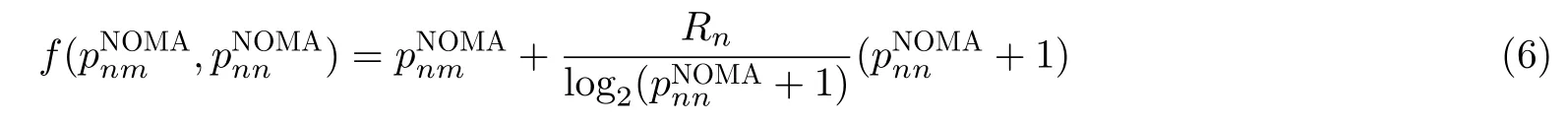
并求出其Hessen矩阵表达式为

上述矩阵存在余子式小于零的情况，因此可得优化目标函数式(4)是一个非凸优化问题。证毕为解决该问题，求出关于和最优的分配策略，本文设计了一种基于深度Q学习网络(Deep Q-learning Network, DQN)的合作博弈算法(DQN C ooperative Game algorithm, DCG)进行求解。

3 .1 基于DQN的合作博弈算法

3.1.1 博弈的第1阶段-竞争

DCG第1阶段需要定义一组竞争关系，根据优化目标函数的影响因子，车辆用户n进行卸载信道选择的过程属于竞争博弈关系，因此定义了用户α和 β 的竞争关系[ α,β]，此时用户n进行任务卸载与对应车辆用户α 和 β 的数学模型fn(α)和 fn(β)分别为

其中， Tα和 Tβ分别表示车辆用户α 和 β 的卸载时延，和分别表示车辆用户α 和 β 的传输功率，用户n进行任务卸载的能耗间隔Δ e如式(12)所示

式(10)和式(11)分别表示用户n进行任务卸载与对应车辆用户α 和 β 的能耗函数，式(12)表示车辆用户n匹配不同用户的能耗差，其中 φ表示任务卸载的能耗缓冲间隙，当满足 C1的约束条件时，任务将用户 β的信道进行混合NOMA-MEC卸载，反之 在用户α 的信道进行任务卸载。

3.1.2 博弈的第2阶段-合作

DCG的第2阶段需要根据目标函数的影响因子定义合作收益θg为

其中， θr和θc分别表示收入因子和成本因子，分别由任务卸载过程中产生时延的倒数和能耗构成。根据上述 公 式， θr和θg成正相关函数，θc和θg成 负 相关函数，因此最优的合作方案是收入因子尽量大，成 本因子尽量小，从而保证车辆用户效益的最大化。

3.1.3 博弈的第3阶段-基于DQN的价格调整

DCG的第3阶段需要通过DQN迭代学习为用户选择最优的卸载策略。DQN是一种将Q学习与神经网络相结合的算法，它使用深度神经网络作为Q值网络，并将Q表的更新问题转化为函数拟合问题，并通过相似的状态获得相似的输出动作，最终通过更新神经网络参数来估算最佳效用值[20]。基于Q学习的深度学习网络模型如图2所示。

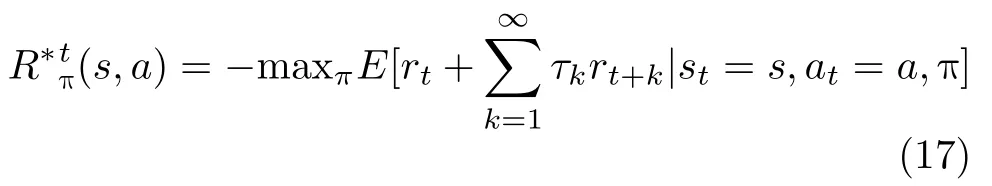
其中，rt表 示最小奖励，τk∈(0,1)表示定义为学习率，表示当前知识对先前学习知识的影响。基于DQN的合作博弈算法如表1所示。

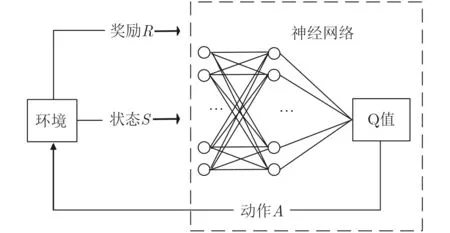
图2 深度学习网络模型图

表1 基于DQN的合作博弈算法

3.2 卸载机制选择

基于上述NOMA-MEC卸载机制的研究，车辆用户在请求完成任务卸载的策略也不再局限于单一的OMA或者NOMA方式，用户可以根据自身任务的属性选择更适合的卸载策略。任务在卸载的过程中会受到很多因素的约束和影响，如任务传输时延、卸载能耗、所需计算资源大小等。混合NOMA-MEC的卸载机制如表2所示。

关于表2的卸载机制，首先初始化任务 qv以及信道容量，并定义了关于用户最优的能耗容忍区间。行(2)定义了用户在NOMA-MEC策略卸载的成本函数，通过行(4)判断当前请求接入的用户数量是否超出在OMA通信网络系统容量，如果当前接入用户数量较少，直接选择传统OMA策略进行卸载，该策略能够减少卸载能耗以及传输成本；如果超过了系统容量则需要通过NOMA-MEC技术解决信道资源不足的问题。行(5)～(11)表示如果用户v 的能耗超出了最佳区间范围，则选择相对能耗表现更为优异的NOMA-MEC策略，如果卸载能耗属于最佳的 范围区间，因此需要比较二者传输时延以及成本。

4 仿真分析

本文基于MATLAB的平台进行仿真，相关网络模型参数设置是在IEEE 802.11p标准和参照3GPP TR36.885进行设定的[21]，假设车辆用户都匀速运动，且在任务卸载期间不会离开原MEC通信范围[22]。部分系统仿真参数表如表3所示。

对于基于DQN的算法，使用两个分别由128和64个神经元组成的隐藏层进行神经网络的设计。选择ReLU激活功能和Adam优化器，其他与DQN相关的参数[23]汇总在表4中。

图3是基于OMA模式、纯NOMA模式、混合NOMA模式下的单一用户卸载能耗图。由此可知，随着任务量的增加，卸载过程产生的能耗也越高；同时NOMA模式下的卸载策略相较于OMA模式会产生更高的能耗，而纯NOMA模式下能耗最高。产生上述现象的原因是NOMA技术能够提高频谱利用率，而香农信息容量理论证明最大频谱效率和最小能耗不能同时达到。

表2 混合NOMA-MEC的卸载机制

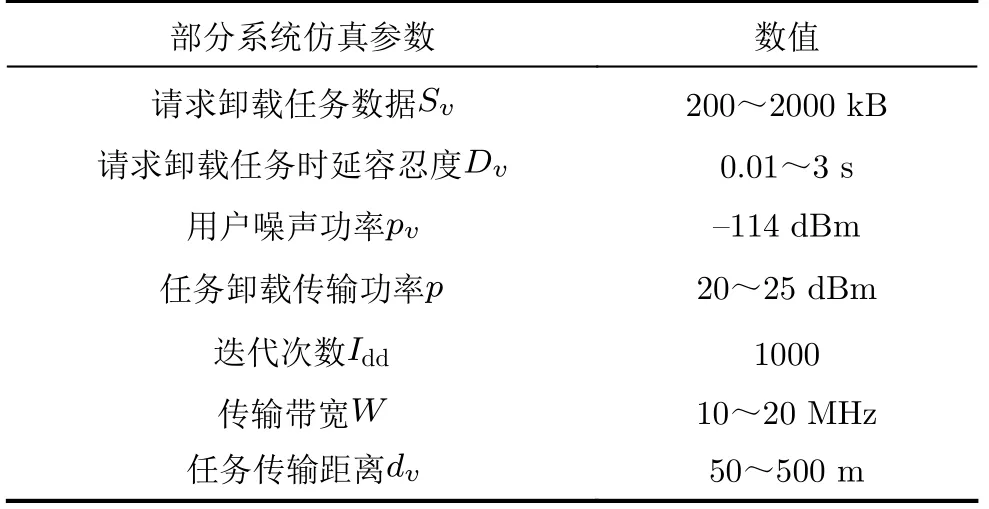
表3 部分系统仿真参数表

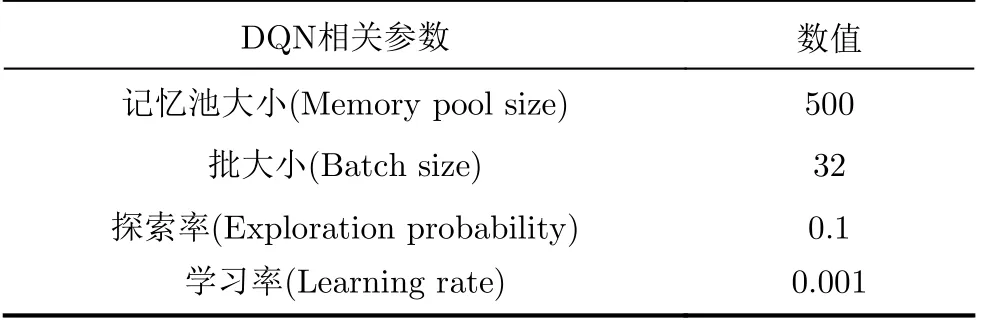
表4 DQN相关的参数

图3 任务大小与能耗关系图

图4是关于请求任务卸载的用户数量与任务卸载总时延的仿真结果。由图可知，随着用户数量的增加，任务卸载的总时延也逐渐增大，同时不同模式下任务卸载的总时延差距也逐渐增加。造成上述现象的原因是，当请求任务卸载的用户数量较少时，3种模式下的信道资源充足，但是随着用户数量增加，信道资源不足的问题逐渐显现出来，传统OMA模式下的用户需要进行任务卸载排序，等待其他用户完成卸载后才能进行卸载，而新型的NOMA卸载策略能够在有限的信道资源下，满足更多的用户同时进行任务卸载。

虽然在纯NOMA模式下总时延最低但能耗却较高，所以通常不采用该方式进行卸载[15]。图5是关于传统OMA卸载与混合NOMA-MEC卸载用户容量的，图中的仿真结果表明，混合NOMA-MEC卸载策略能够在有限带宽的约束条件下，为更多的车联网用户提供卸载。通过计算结果得出，该策略相较于OMA模式下的卸载，卸载用户容量提高约50%，因此混合NOMA-MEC卸载策略能够有效地解决多用户卸载信道不足的问题。

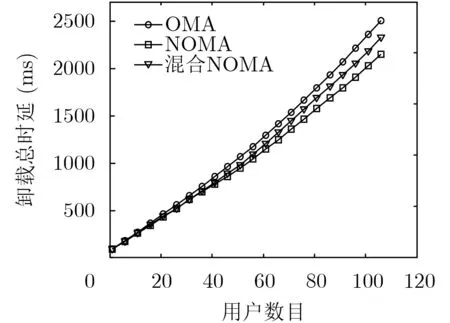
图4 用户数目与总时延关系图

图5 带宽与用户容量关系图

在总开销计算中将 λ的值设为[0.1, 0.5, 0.9][24]，来体现系统在不同情况下对时延和能耗的要求不同。当λ =0.1时，系统对时延的要求极高，图6(a)展示了在这种情况下，OMA模式卸载与混合NOMAMEC模式卸载的总开销差异。结果显示在系统对时延要求高时，混合NOMA-MEC相比OMA模式有较低的总开销。图6(b)展示了当λ =0.9时，系统对能耗的要求极高的情况下，混合NOMA-MEC的开销却大于OMA模式的总开销。这是因为NOMA虽然可以容纳更多的用户减少卸载时延，但会同时付出高能耗的代价。

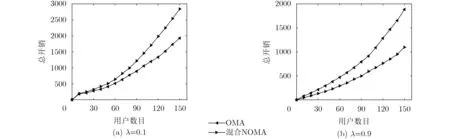
图6 时延和能耗要求不同时用户数目与总开销关系图

将提出的DCG算法与几何规划算法(Geometric Programming, GP)[15]对比。图7是当λ=0.5时，时延和能耗视为同等重要时，用户请求任务卸载的数目与总开销的关系。通过对比分析发现，混合NOMA-MEC的卸载策略相较于OMA模式开销更小，主要原因是混合NOMA-MEC的卸载决策是一种更加全面的卸载策略，它同时考虑了任务卸载过程中时延的要求和能耗的影响，因此该卸载模式能够最大化地保证用户效益。且随着用户数目的增加，在进行任务卸载的过程中将会产生更多的开销，在两种卸载模式情况下，本文算法DCG都优于GP算法，是因为在考虑了NOMA和MEC组合的复杂性的情况下，车辆用户能更动态地选择卸载模式。

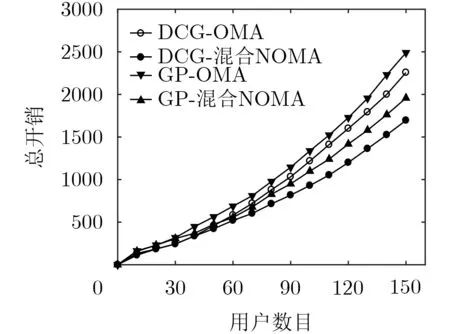
图7 λ = 0.5时用户数目与总开销关系图

5 结束语

本文提出了车联网场景下混合NOMA-MEC的卸载策略，解决了现有通信网络模型中信道资源不足的问题，该策略能够在有限的信道带宽资源约束下，为更多的请求用户提供卸载。本文采用了博弈算法为用户进行信道选择，在此基础上设计了DCG算法，有效地帮助用户选择最优功率分配策略，最大限度的保证卸载用户的效益。仿真结果表明，在系统对时延和能耗要求相同时，混合NOMA-MEC卸载策略更加全面地优化了目标函数，使得总开销显著降低。在未来的研究工作中，将进一步研究任务卸载过程中面临小区切换的问题。