贝叶斯极限梯度提升机结合粒子群算法的电阻点焊参数预测

邓新国 游纬豪 徐海威

①(福州大学数学与计算机科学学院 福州 350108)

②(福建星云电子股份有限公司 福州 350000)

1 引言

动力电池组的电阻点焊是一个既有静态变量叠加影响又有热、力、电等动态变量相互耦合的高度非线性过程[1,2]。在达到合格的焊接效果之前，需要结合人工经验进行大量的试样，尝试各种焊接参数组合，才能得到目标值的最优参数，从而造成时间、材料消耗多等问题。国外学者Pandey等人[3]利用田口法对低碳钢进行电阻点焊实验，统计分析电流、时间、电极压力对抗拉剪载荷的影响，得到较优工艺参数。Arunchai等人[4]把焊接时间、电极压力、电流作为神经网络的输入，抗拉剪载荷作为输出，得到了预测焊点强度的模型。Pashazadeh等人[5]利用神经网络与多目标遗传算法对标准钢板进行点焊工艺参数优化，获得了最佳工艺参数搭配。Wan等人[6]利用径向基神经网络建立了微电阻焊接质量的预测模型。国内学者王先逵和赵杰[7]通过模式增强和函数连接网络实现了焊接工艺过程的分类学习和自动识别。赵大伟等人[8]利用灰色关联分析研究钛合金微电阻焊接参数对焊接质量的影响，得到了工艺参数的最优组合。高星鹏等人[9]使用正交实验极差分析研究焊接参数对焊接质量的影响，通过遗传算法和神经网络对点焊工艺参数进行优化，并把多目标优化问题转为单一混合目标优化，得到良好的焊点力学性能预测模型。刘伟和郭猛[10]提出将Logistic映射微粒群优化算法和BP神经网络结合的方法，对08AL钢板点焊工艺参数建模优化，得到三大主要工艺参数的最优组合。舒服华和王志辉[11]提出将神经网络和蚁群算法结合的模型，对08AL钢板电阻点焊工艺参数进行优化，通过仿真实验显示了该方法的有效性。

从上述文献来看，正交实验等统计法对于了解各参数对模型的影响具有良好的辅助作用，但无法全面考虑实际参数的取点问题。神经网络因其极强的非线性映射能力，在模拟点焊过程上有很好的表现，不过其缺陷是易在小数据集上陷入过拟合，导致实测中准确率下降[12]。且大多数文献仅对目标值的最大值进行优化，未考虑到可变目标值的问题。本文针对以上问题提出贝叶斯极限梯度提升机(Bayes eXtreme Gradient Boosting, Bayes-XGBoost)结合粒子群算法，在厚度为0.15 mm的镍片和0.4 mm的不锈钢电池正极帽上实验，获取实际工况中的电阻点焊数据。其特征包括焊接压力、焊接电压1、焊接电压2、焊接时间1和焊接时间2，其中1, 2代表两段焊接过程，该目标值为抗拉剪载荷。利用极限梯度提升机(eXtreme Gradient Boosting,XGBoost)和粒子群算法进行建模预测，通过XGBoost的非线性切分能力和防控过拟合机制构建点焊工艺参数到目标值的模型，然后通过粒子群算法在模型中为需求值寻找最优的工艺参数[13,14]。将XGBoost正向训练与粒子群算法反向预测结合，获得可变目标值的工艺参数。XGBoost超参数众多，故采用贝叶斯算法对参数进行联合优化，选取全局最优的超参数[15]。设定的目标值不是最大抗拉剪载荷值，而是根据具体需求变化而定，对于不同的领域如汽车、列车和航空材料等，需要的目标值均不同，该设计思路体现在粒子群算法的目标函数设定。在测试集上对Bayes-XGBoost做正向训练的对比实验，对Bayes-XGBoost+粒子群做整体预测的对比实验，来检验该模型的有效性。

2 Bayes-XGBoost+粒子群算法

2.1 XGBoost算法

电阻点焊工艺参数相互干扰共同影响，对焊接质量的影响呈非线性关系[16]。集成学习算法具有良好的拟合和泛化能力，其中XGBoost具有强大的非线性切分能力以及较好的防控过拟合机制，适合本问题的研究。

XGBoost由多个基分类器联合决策，先训练前k-1棵 决策树，再训练第k 棵决策树，第k 棵树的输入与前面树的残差相关。树的预测函数为

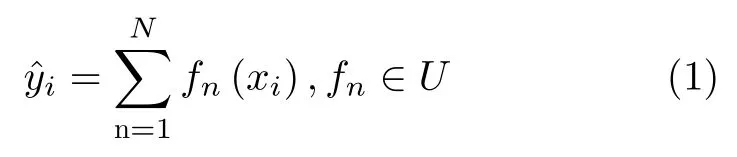
其中，xi为 样本，为 结果，U 是树集合。通过多个决策树使预测值一步一步接近真实值，训练的目标函数为

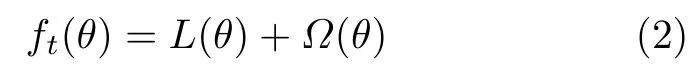
其中，L (θ)为 误差，Ω (θ)为正则化项。学习过程中保持之前模型不变的基础上加入新项fk，若目标函数减小，就把fk加入模型。XGBoost利用目标函数的2阶导数进一步增强了拟合能力。正则化项Ω(θ)即树的复杂度，如式(3)

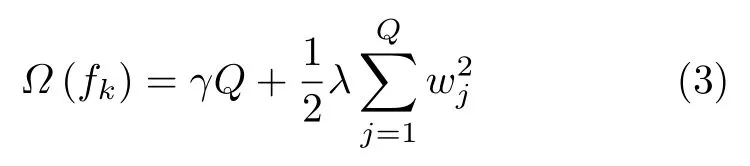
其中， w 为叶子权重，Q 为叶子个数，γ , λ用于增强模型防控过拟合能力。

XGBoost算法的学习过程是对枚举的决策树结构做最优决定，根据贪心策略不断选择增益最大的节点。最优化分裂停止条件有3个，即引入的分裂增益小于设定阈值，树深达到最大深度，样本权重和 小于设定阈值[17]。

2.2 贝叶斯优化算法

贝叶斯优化算法是一种基于概率分布的算法，通过先验函数表示分布假设，使用采集函数决定采样位置。可以决定参数集合的下一步采样，集成了不确定性[18]。针对XGBoost的参数选择，先验函数选择高斯过程，表示优化函数的分布假设；采集函数选择提升概率(Probability Of Improvement,POI)函数，从后验分布中选取下一组参数并评估。

高斯过程指XGBoost算法的参数组合，有限个数的组合都存在一个联合高斯分布

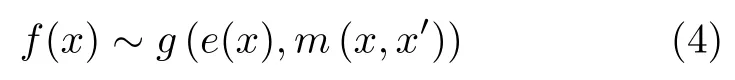
其中e (x)=E(f(x))， 即期望，m (x,x′)是 x 的协方差，f(x)是 平均绝对误差。对于组合X ={x1,x2,···,xj}，把{x1:j,f1:j}加入样本后，联合高斯分布变化，同时得出后验概率。

采集函数的思路是选取一个能让最大值以最大概率提高的点。目标是在集合 S中寻找使函数f(x) 达到全局最优的取值x，即

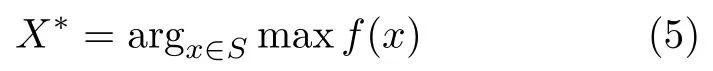
利用贝叶斯优化选取XGBoost参数的流程：初始化参数集合，送入高斯模型中，将样本送入预测模型，根据输出对高斯模型修正。若加入的组合达到误差要求就终止优化过程，否则采集函数选取下一组参数，根据误差修正高斯模型并进行下一组参数评估[19]。

2.3 粒子群算法

粒子群算法是一种启发式优化算法，在状态空间中对每一个位置进行评估，得到最优位置和最优目标值。每个粒子是多维空间中的搜索个体，个体位置为候选解，飞行过程即寻优过程，速度和位置根据历史最优位置和群体最优位置更新。速度、位置更新公式为

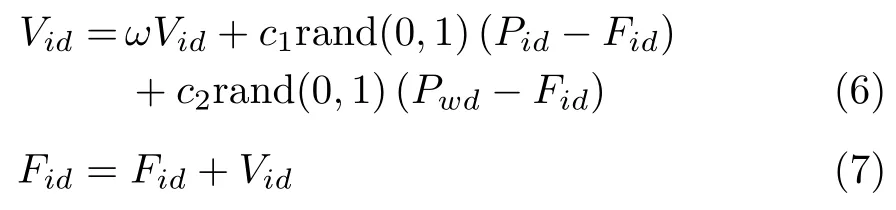
其中， Vid是个体速度，Fid是个体位置。ω 是惯性因子，控制速度变化， ω取较大值时模型的全局寻优能力强，局部寻优能力弱；取较小值时模型的全局寻优能力弱，局部寻优能力强[20]。 c1和 c2是加速参数，rand (0, 1)是[0, 1]内的随机数， Pid是第i个变量的个体最优值的第 d 维，Pwd是当前全局最优解w的第 d维。把位置信息送入目标函数计算个体和群体的历史最优位置及最优适应度值，不断迭代更新，直至达到终止条件[21]。

之前电阻点焊优化的目标是寻求抗拉剪载荷的最大值，值越大点焊质量越好[22]。本文的目标是大于需求值，且与需求值相差越小越好。故将p (抗拉剪载荷)与n (需求值)的差作为粒子群的目标函数，如式(8)所示

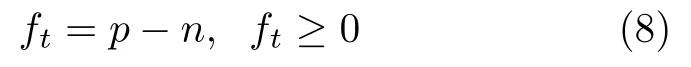
3 电阻点焊参数预测方法

本文算法结合了贝叶斯优化算法，XGBoost算法和粒子群算法，如表1所示，整体分为两部分：XGBoost模型的训练过程和粒子群算法的寻优过程，对应表1中的步骤1和步骤2。第1部分的准备工作包括对焊接数据进行归一化和切分，对算法的参数进行初始化，对应步骤1。然后是XGBoost的正向训练，同时利用贝叶斯优化搜寻最佳参数，对应步骤2。每次贝叶斯优化选择参数的过程即XGBoost的一次训练过程，XGBoost的训练是一个不断迭代的过程，在未满足停止条件之前不断进行最优化分裂，对应步骤2.2。贝叶斯优化的停止条件是满足误差要求，否则迭代进行步骤2.1～2.3。在XGBoost训练完成，形成虚拟的映射函数后，利用粒子群算法对映射函数进行反向搜索求解，对应步骤3。第2部分首先初始化粒子群，根据需求值按公式设定目标函数。未满足停止条件前不断迭代，对应步骤3.1～3.3。最终得到全局最优预测结果。

算法复杂度分为3部分，XGBoost的时间复杂度主要消耗在学习树，树在搜索、分裂结点时需要对每个特征遍历所有样本，通过计算增益获取可能的分裂结点，样本数为 N ，特征数为W ，时间复杂度为O (N ×W)，因为做了列分块优化，特征维度并行训练，分块数为B ， 故时间复杂度为O (N ×W/B)。训练数据可以当作一个 N ×W的超大规模稀疏矩阵，空间复杂度为O (N ×W)。贝叶斯优化主要是根据已有结果建模高斯过程，计算量消耗在计算协方差矩阵的逆，时间复杂度为O (N3)，但也优于网格搜索和随机搜索。空间消耗主要在样本空间上，空间复杂度为 O (N)。粒子群算法的时间复杂度与粒子个数 M 、维度数C 、循环次数 T有关，时间复杂度为O (M ×C×T)， 空间复杂度为O (M ×C)。

整个算法的时间、空间复杂度占比主要在XGBoost，但实现过程对内存、IO, CPU cache均做了优化，所以其速度大大加快。而且XGBoost加入了正则项，限制树的复杂度，既保证了泛化能力，又减小了空间复杂度。实验结果5.3.2节中有具体 的时间对比。

表1 Bayes-XGBoost+粒子群算法

4 实验样本获取及模型参数设置

4.1 实验数据获取

结合文献[1,2,4,10,23]以及实际经验，选择对焊接结果有重要影响的参数，即焊接压力、焊接电压1、焊接电压2、焊接时间1、焊接时间2作为输入参数；点焊工艺质量以点焊接头的力学性能参数抗拉剪载荷为指标，抗拉剪载荷为抗拉强度和抗剪强度的综合指标[23]。为了保证实验数据的均匀分布，尽可能全面模拟真实环境，结合实际点焊工程经验和设备可调范围进行取点，各个焊接参数的范围见表2，焊接结果参数抗拉剪载荷值在90～180 N。共计1280个组合，舍去极限状态下以及不符合工程要求的选点，剩余576个组合。因存在工艺不稳定性，每个组合需进行不少于5次的重复测量，对多次测量结果进行取最小值，取最小值的原因是最终预测的结果是要大于需求值的，若最小值大于需求值，则普通情况均满足需求值。

表2 参数范围

使用厚度0.15 mm的镍片和0.4 mm的不锈钢电池正极帽在米亚基8000BMAD上焊接，该机器最大功率99.9 kW，最大电压10 V，焊接时间可精确到0.1 ms。

4.2 模型参数设置

贝叶斯优化XGBoost的参数集合主要包含3类参数：Booster参数、通用参数、目标参数，如表3所示。

为平衡算法的搜索能力和计算量，粒子群算法的种群规模 S取50，迭代次数500，粒子维度5，控制加速的因子 C1=C2= 1.49，惯性权重W =0.729，粒 子解空间范围是[0, 1]。

5 实验结果

5.1 贝叶斯优化结果

利用贝叶斯优化搜寻XGBoost的参数，并与网格搜索法做对比，将迭代误差绘制成图1。其中，横坐标是迭代次数，纵坐标是测试集的误差均方(Mean Square Error, MAE)指标，由式(9)得到

表3 XGBoost参数集合

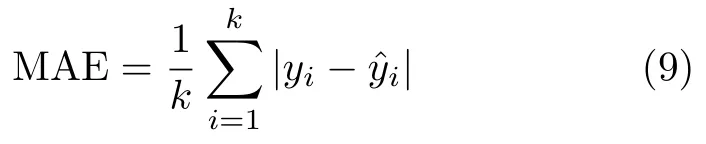
其中， k为样本个数，| yi-|为真实值与预测值的绝对误差。网格搜索初始误差较大，最终达到0.0314，贝叶斯优化在经过约80次迭代达到稳定，误差降至0.0151。可知贝叶斯优化XGBoost的参数优于网格搜索，使整体算法具有良好的预测能力。参数如表4.

5.2 XGBoost算法结果

利用表4参数训练XGBoost，得到电阻点焊模型。为了解哪些特征对于XGBoost模型最重要，绘制出每个样本的每个特征的shap值，shap是一种博弈论方法，用于解释机器学习模型的输出，代表特征对模型输出的贡献。图2是对特征进行排序的结果，依据是所有样本的shap值重要度，显示出每个特征对模型输出的影响，推高预测以红色显示，推低预测以蓝色显示。

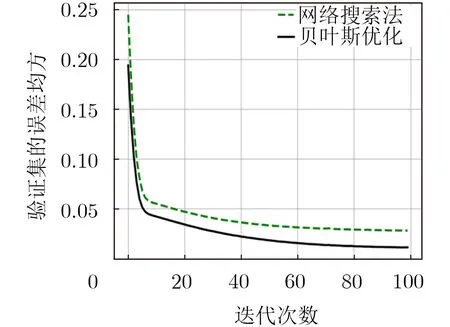
图1 两种搜索方法的结果

表4 XGBoost参数

特征值0～4分别为焊接压力、焊接电压1、焊接电压2、焊接时间1、焊接时间2。特征对输出的影响程度从高到低为焊接电压2、焊接电压1、焊接压力、焊接时间2、焊接时间1。可看出第2段电压对结果的影响是最大的，超过临界点后焊接效果会变差。随着焊接压力增大，在临界点之前抗拉剪载荷逐渐增大，在临界点之后，抗拉剪载荷逐渐减小。电极压力过大导致接触电阻减少，压痕变大，故点焊强度变弱[10]。

可视化训练过程用热力图表示，如图3所示，横坐标为每个样本，纵坐标为基值变化。热力图根据博弈论得到，意义为每个样本从基值到输出的推入过程，红色代表存在特征推高基值，蓝色代表存在特征推低基值。

表5是预测结果的对比，TRAIN-MAE为训练集的MAE, TEST-MAE为测试集的MAE。可知贝叶斯优化XGBoost优于随机森林 (Random Forest,RF)、后向传播神经网络 (Back Propagation,BP)、网格搜索极限梯度提升机 (Grid search eXtreme Gradient Boosting, Grid-XGBoost)，且误差满足需求。

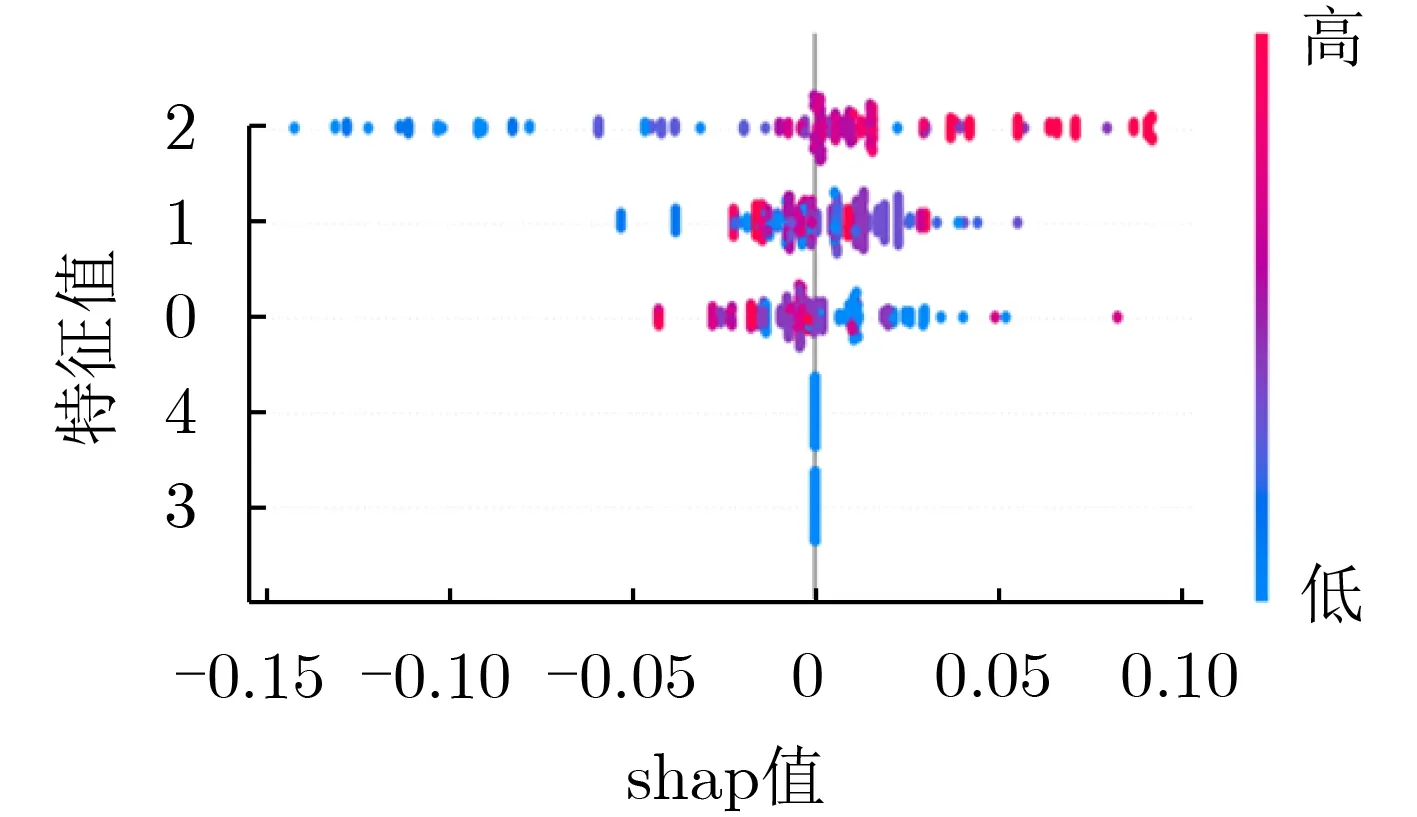
图2 特征对模型输出的影响

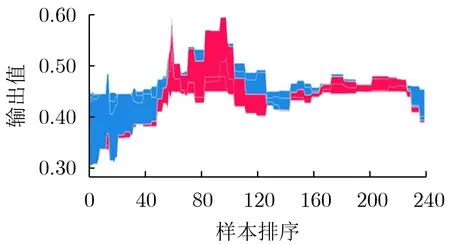
图3 可视化训练热力图

5.3 粒子群结果

5.3.1 粒子寻优过程

点焊出现频率最高的需求值是130 N，以此为例观察粒子群的变化，图4为粒子在搜索空间的初始化和迭代结束的结果，图中横纵坐标为解空间的两个维度，单位已归一化，范围均在[0, 1]。可见粒子最终收敛效果较好。经过约300次的迭代后，获得稳定的全局最优目标值，此时最优值为130.02 N。

5.3.2 多种指标结果对比

为了更加直观地证明整体模型的工程实用性，直接计算Bayes-XGBoost+粒子群算法的整体误差。使用粒子群预测得到的参数在实际环境中测试，此时实测结果从全局角度看相当于整体模型的预测值，而需求值作为真实值，输入误差指标中计算误差。这样做相当于还原了问题的本质，直接检验需求值与模型结果实测值的差异。

在真实环境下通过实测验证最优化预测结果的有效性。在抗拉剪载荷的取值范围90～180 N内取点，每隔5 N取1个采样点作为焊接需求值，每个需求值用4种算法分别预测焊接参数，得到的最优化预测参数在实际环境中做点焊测试，每组参数做5次实验取平均，得到稳定的最优化预测结果。为了验证模型的有效性，采用以下两种误差评价指标：均方根误差(Root Mean Square Error, RMSE)、希尔不等系数(Theil Inequality Coefficient, TIC)，它们的计算方式如式(10)和式(11)所示

表5 模型预测结果

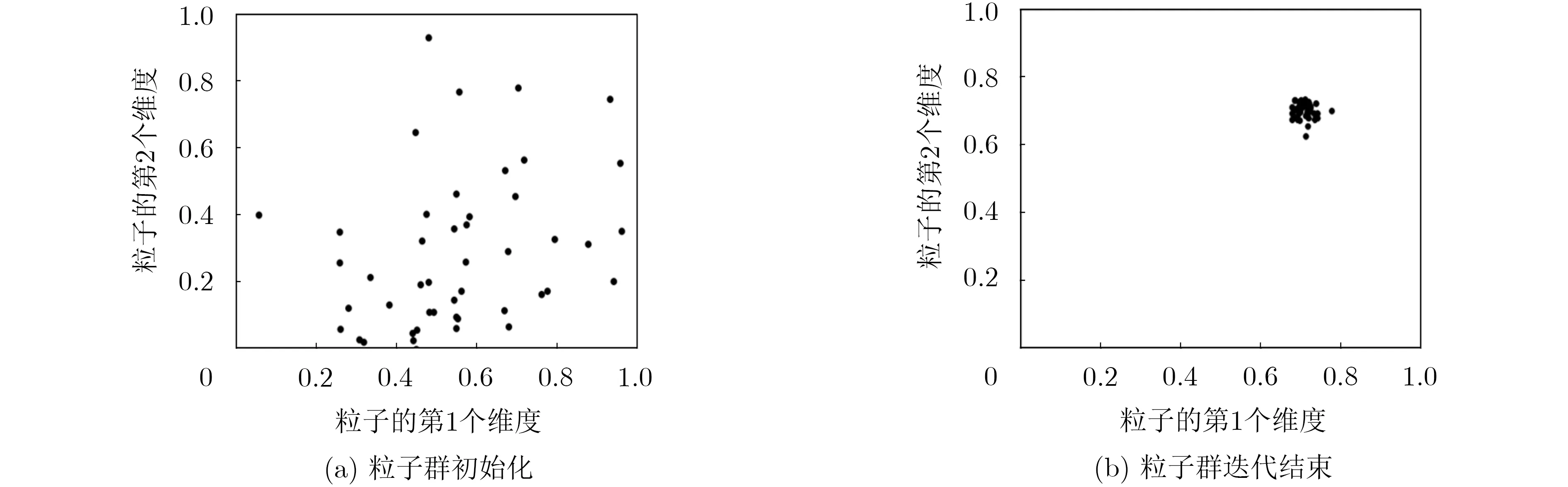
图4 粒子初始化及迭代结束的分布

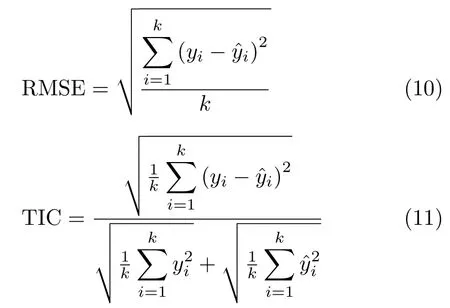
其中，k为样本个数，yi与是需求值以及最优化预测的实测结果，误差指标均是越小越好，结果如表6所示。

Bayes-XGBoost+粒子群算法在两种误差指标中均低于其余方法，并且误差值减小至实际工艺要求范围内。

预测误差不能完全证明算法的有效性，实际工艺要求是结果大于需求值，高于需求值5 N比低于需求值0.1 N更优，准确率也是衡量算法的重要标准，用实测合格个数除以总个数得到准确率，表7是准确率对比。

可以看出Bayes-XGBoost+粒子群准确率最高，同时在处理大规模数据集时，算法效率也要考虑，表8是速度对比。

XGBoost在使用多核多线程的时候能够发挥很强的性能，处理大数据时具有速度优势。经过多种算法的误差指标、准确率、执行效率对比后，证明Bayes-XGBoost+粒子群算法的综合性能较强，在对电阻点焊参数进行预测的时候具有很好的效果，能对实际点焊工艺提供有效的辅助作用。

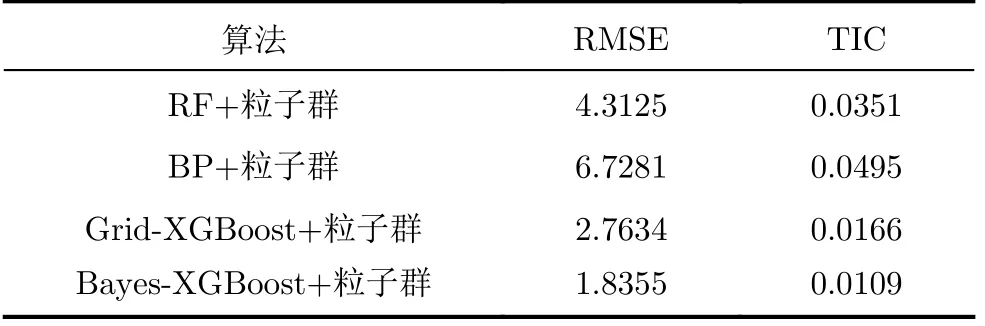
表6 算法的误差

表7 算法的准确率

表8 算法所用时间

6 结论

准确预测可变需求值的工艺参数可以极大地减少时间和材料耗费，但点焊工艺的不稳定性以及数据规模都增加了预测的难度，提出一种能够全面模拟点焊过程，且具有防控过拟合能力的方法是很有意义的。本文通过构建576组点焊样本，利用XGBoost算法对点焊过程进行建模，引入贝叶斯优化自动搜寻参数，通过与其他算法的对比实验表明XGBoost对电阻点焊过程具有良好的拟合和泛化能力。然后利用粒子群算法对已形成的正向预测模型搜寻可变目标值的工艺参数，反向预测最优参数。在与其他算法对比后，验证Bayes-XGBoost+粒子群算法对可变目标值的工艺参数预测具有较高的可靠性，在误差、准确率、效率上均有优秀表现。有助于工程师在新的需求值上快速选取合适的工艺参数，提升了效率。