基于多维时空的NPCA-PSR-IGM(1,1)组合模型的短时交通流预测

殷礼胜 高 贺 魏帅康 孙双晨 何怡刚

(合肥工业大学电气与自动化工程学院 合肥 230009)

1 引言

智能交通的发展与社会经济的发展的联系愈加紧密，智能交通系统的研究已然成为当今热点研究课题[1,2]。短时交通流预测是实现交通诱导和控制的关键，同时也是智能交通系统管理的基础[3,4]。短时交通流具有较强的混沌性和非线性等，各专家针对其特点提出很多智能预测模型和算法。梅朵等人[5]采用主成分分析(Principal Component Analysis,PCA)与遗传粒子群支持向量机结合的方法来预测交通流量，该方法有效地简化了预测路段时空相关性极强的多个交通流预测变量，但其忽略了交通流量的非线性以及序列的混沌性。王科伟等人[6]采用多维相空间重构(Phase Space Reconstructed,PSR)对交通流数据进行混沌时间序列分析，但该模型没有考虑城市交通的空间特性以及交通流量的非线性。钱伟等人[7]采用组合模型的短时交通流量预测，该模型具有训练时间短、抗干扰性强的特点，但该方法所需大量历史交通流量数据，对于采集数据较少的情况，结果未知。佟健颉等人[8]采用基于时空关联性的深度残差网络预测算法，该算法考虑到交通流量数据的时空相关性并利用深度残差网络进行预测，从而提高预测精度，但其忽略了交通流数据的非线性和混沌特性。

从多维时空交通流量序列的非线性、混沌的内在规律角度来看，以上研究有的忽略了序列的非线性或者序列的混沌性甚至两者均没考虑。综上所述，本文针对这些研究的不足在构建模型时，考虑交通流量序列的非线性的同时结合序列的混沌性，尝试提出一种基于多维时空的非线性主成分分析和相空间重构的改进灰色(NPCA-PSR-IGM(1,1))组合预测模型。并用该模型对合肥市芜湖路与徽州大道交叉口部分交通流量进行预测和对比分析，通过NPCA-PSR-GM(1,1)组合预测模型、PCA-PSRIGM(1,1)组合预测模型以及文献[7]和文献[8]所提出的预测模型的预测值的比较，以验证本文模型在精度提升上的优越性。

2 多维时空NPCA-PSR-IGM(1,1)组合预测模型相关理论

2.1 基于多维时空交通流量相关性的非线性主成分分析原理

对 p个路段的采样点进行交通流量数据采集，每个路段等时间连续采样l 次 ，即p 为路网中空间的数量， l为各空间中等时间采样次数，可以表示为Y1,Y2,···,Yp， 其中Yi=(yi,1,yi,2,···,yi,l), i =1,2,···,p。计算各观测点与预测点交通流量序列的相关系数ρj，定义为

建立协方差矩阵R 并计算特征值和特征向量。

2.2 多维时空交通流量序列的混沌相空间重构原理

已知多维时空交通流量序列经过数据相关性的非线性主成分分析后，将原始序列在空间和时间上降维，得到交通流量序列 X1,X2, ···,Xm，其中Xi=(xi,1,xi,2,···,xi,n), i =1,2,···,m。根据Takens嵌入定理[10]，研究复杂的多维时间序列数据首先需要进行相空间重构。其主要目的是构造出表征原序列的高位空间特性。对上述多维序列重构相空间如式(4)。

将多维时空交通流量序列进行相空间重构后，每个相点代表交通路网的一个状态。假设相点Vk的最邻近相点Va， 则Vk和 Va之 间的距离为Zk

其中，vj.i=[xj,i,xj,i+τj,···,xj,i+(dj-1)τj]; xj,i表示路段 j 的 第i个交通流量。

2.3 多维时空相空间重构的改进灰色模型IGM(1,1)

常规灰色模型GM(1,1)的1阶线性微分方程为

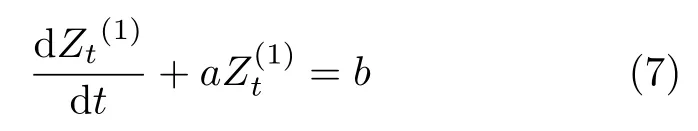
解方程得

其中，参数a, b，可按最小二乘法求得。

一般的指数形式为 y =aeb(x-c)+d ，其中a,b,c,d均为待定参数，而为了确定其形式至少需要4 点，为便于计算这里简化指数一般形式为y =aex+b，此时有

因此改正后的背景值为

通过上式背景值的改进，建立改进的灰色模型IGM(1,1)。由于改进的背景值比常规的背景值更加接近于实际，所以误差更小。

3 基于多维时空NPCA-PSR-IGM(1,1)组合预测模型构建与算法

本文选定合肥市芜湖路与徽州大道交叉口出口处作为预测点，取样时间为2018年10月15日上午7点到8点45分，时间间隔5 min记录1次。本模型不失一般性，为节省篇幅不再考虑晚高峰。如图1可知，预测点主要受到附近6个观测点的影响，共得6组数据，每组22个时间点交通量作为实验数据，取每组前16个时间点交通流量作为拟合数据，记为Y1,Y2,···,Y6， 其中，Yi=(yi,1,yi,2,···,yi,16), i=1,2,···,6 。预测点Y1的后6个时间点的交通流量作为预测 对比真实值。

3.1 数据相关性的主成分分析降维

取路网中的6个采样点，分别为观测点1-观测点6，其中观测点1也是预测点。各观测点与预测点按式(1)进行数据相关性分析，计算得到各点相关系数ρ，结果见表1。

一般认为相关系数取0.7以上为强相关[13]。由表1可知，影响预测点交通流量的主要因素有观测点1、观测点2以及观测点3的交通流量，见图1中虚线圈内所示。

图1 芜湖路与徽州大道交叉口示意图

表1 各观测点与预测点交通流量数据相关系数

3.2 多维时间序列的相空间重构参数的选取

结合多维时空交通流量序列的情况，使用自相关法计算各序列的延迟时间，得τi=1, i =1, 2, 3。使用GP算法[14]，对观测点1的交通流量序列算出在不同维数下 ln r 和l n C(r) 的值，将嵌入维数d1=1至d1=6情况下的曲线绘制如图2所示。

若去除曲线斜率为0和斜率为 ∞的直线段，每条曲线所包含的直线斜率，可作为各嵌入维数对应的关联维数，结果如表2所示。

由表2 可知饱和关联维数 D趋于0.5，因d1≥2D+1，则可确定嵌入维数2。路网中各路段采样点的交通流量序列的嵌入维数按照上述方法计算得到，同时由 M =n-(d-1)τ计算对应的嵌入相点数。由于附近各路段交通环境的相似性和复杂性，一般取各维交通流量序列的嵌入相点数中最小作为统一的相点数[15]，从而得知，多维时空交通流量序列的嵌入相点为

3.3 多维时空的NPCA-PSR-IGM(1,1)组合预测模型

表2 观测点1的嵌入维数与关联维数

图3 多维时空NPCA-PSR-IGM(1,1)组合预测模型

3.4 基于多维时空的NPCA-PSR-IGM(1,1)组合预测算法

短时交通流的非线性和混沌性特征，很难采用单一的预测方式得到较好的预测结果。本文采用数据相关性的非线性主成分分析和相空间重构的改进灰色组合预测算法对短时交通流进行预测，具体预测步骤如下：

步骤 1 对多维时空交通流量序列进行空间降维。首先，对p 个路段等时间间隔连续采样l次，得到多维时空交通流量数据，然后由相关系数求解公式计算各观测点与预测点的相关系数ρj(j =2,3,···,p)，从而剔除与目标路段相关性较低的观测点，此时路段数为m (m =3)。

步骤 2 利用步骤1得到空间降维后的交通流量序列，进行时间维度上的非线性主成分分析。由累计方差贡献率的计算公式确定主成分的个数n(n =13)，相应的累计方差贡献率取8 5%∼95%时，也就说明前 n个的采样序列已经包含了对预测点影响较大的主要信息。

步骤 3 对降维后的交通流量序列进行相空间重构。首先，计算各交通流量序列的延迟时间 τi和嵌入维数 di(i =1,2,···,m ) ，其次，由M =n-[(Di-1)Ti]从 而得到重构后的多维相点数 M(M =12)，所以重构后的相空间向量可表示为Vi(i =1,2,···,M)。

步骤 4 找到每个相点的最邻近相点并计算出其值，得到相点的最邻近相点距演变序列 Z：

Z =(Z1,Z2,···,ZM)。

步骤 6 建立

步骤 7 求得相点距离后，反演计算相点的位置，即得交通流量的预测值。设时刻 k 的相点Vk的最邻近相点为Va, Vk与 Va距离为

其中， vj.i=[xj,i,xj,i+τj,···,xj,i+(dj-1)τj];可由灰色预测得出，仅xk,i为未知的预测值，通过解式(12)方程可以得出xk,i。

步骤 8 输出预测点的预测值。

4 实验结果与分析

4.1 评价标准

本文以平均相对误差和标准偏差为评价模型预测精度的好坏的标准，平均相对误差和标准偏差公式分别为

4.2 实验对比与分析

本文分别使用基于多维时空的非线性主成分分析和相空间重构的常规灰色(NPCA-PSR-GM(1,1))组合预测模型(如图4)、基于多维时空的主成分分析和相空间重构的改进灰色(PCA-PSR-IGM(1,1))组合预测模型以及基于多维时空的非线性主成分分析和相空间重构的改进灰色(NPCA-PSRIGM(1,1))组合预测模型进行拟合仿真，以此分别对预测点后6个时间点(序列号17～22)的交通流量进行预测，预测点的真实值与3种组合预测模型的预测结果趋势如图5所示。由图5进一步分析可以得到3种组合预测模型预测的平均相对误差和标准偏差如表3所示。

图4 基于多维混沌时空NPCA-PSR-IGM(1,1)组合预测算法流程图

由图5可知，基于多维时空的NPCA-PSRIGM(1,1)组合预测模型预测效果更好，基于多维时空的PCA-PSR-IGM(1,1)组合预测模型其效果最差。由表3可知，该组合预测模型相对于NPCA-PSRGM(1,1)组合预测模型和PCA-PSR-IGM(1,1)组合预测模型其预测结果的平均相对误测分别下降了3.12%和7.53%，同时其标准偏差分别从6.4336下降到2.0589和15.7091下降到2.0589。为了证明本文所提组合模型的优劣，将组合预测结果与文献[7]以及文献[8]所提出的预测方法进行对比，预测点的真实值与最新预测模型的预测结果趋势如图6所示。同时，得出性能指标如表3所示。

图5 3种组合预测模型预测结果图

表3 3种组合预测模型预测误差统计

图6 本文组合预测模型与最新模型预测结果

由图6的预测结果，结合表3预测性能指标可以看出，在实际获取的交通流量数据较少的情况下，文献[7]所提出的组合预测模型其优势没有得以体现并不能达到较好的预测效果。同时，文献[8]所提出的基于时空关联性的深度残差网络预测模型，虽然考虑到短时交通流量数据的时空相关性，利用大数据进行深度学习构建深度残差模型，达到不错的预测效果，但本文所提出的组合预测模型不仅涉及交通流量的时空相关性，而且考虑到交通流量数据的非线性以及混沌性，从而进行非线性主成分分析剔除无关数据和利用多维时空相空间重构凸显交通流量数据的内部规律，进一步提高预测精度。

5 结束语

本文首先运用数据相关性的非线性主成分分析对多维时空交通流量序列进行时空降维，其次应用多维时空相空间重构放大交通流量序列的内部细微特征，最后结合改进灰色模型在保留传统模型易于计算的优点的同时在预测精度上也有所提升。通过仿真结果可知，该组合预测模型相对于多维时空NPCA-PSR-GM(1,1)组合预测模型、多维时空PCA-PSR-IGM(1,1)组合预测模型以及一些最新的预测模型有着更高的预测精度。这种组合模型为短时交通流预测提供了一种新的想法，但本文没有就天气和不同节假日因素对路段的影响，因此这将是本文研究的下一步内容。