基于大通讯时滞的二阶多智能体系统的一致性分析

晋守博 魏章志 李耀红

(宿州学院数学与统计学院 宿州 234000)

1 引言

多智能体系统广泛应用于生物学、计算机、管理学和工程学等方面，如鸟群的飞行、蚁群的协同合作、鱼群的巡游和无人机群表演等[1,2]，这些现象都可以利用多智能体系统构造数学模型解决。本文将研究定向通信拓扑下2阶多智能体系统的一致性与鲁棒性，该问题的关键点是设计通信协议，并在该协议下分析随着时间的变化，所有智能体是否能够达到相同的状态。自从一致性的定义在文献[3]中被提出后,许多学者从不同的方面开始陆续关注该问题。最近，文献[4,5]的成果将多智能体系统的一致性问题的研究推向了一个新的阶段，随后文献[2]讨论了相关问题的理论框架，并给出了一致性算法。另外，蒋国平等人[6]从不同方面介绍了一致性问题的相关研究成果，并且指出仍然有许多难题需要学者去解决,关于一致性问题的进一步研究可参考文献[7,8]。

一般情况下，多智能体系统常用微分方程组描述系统的变化规律，既有低阶的情况也有高阶的情况，往往随着阶数的增高，系统会变得更加复杂。一阶多智能体系统对应着一组一阶微分方程组，这种系统结构相对简单，主要是反映智能体位置的变化规律，目前已经有很多这方面的研究成果；2阶多智能体系统虽然结构复杂，但是能够同时描述智能体位置和速度的变化情况，而且2阶系统现实意义更强。针对2阶多智能体系统，文献[9,10]分析了实现一致的充要条件，文献[11]讨论了有限时间一致性问题，文献[12]在随机扰动下研究了系统的一致性。另外，ZHENG等人在文献[13]中讨论了混合阶多智能体系统的一致性。本文将考虑如式(1)2阶多智能体系统

为了降低时滞对系统式(1)的影响，需要设计新的一致性协议，首先将输入变量中的xi(t-τ)和 vi(tτ)替 换为xi(t-τ +β)和 vi(t-τ +β)， 此时常数β 无法直接控制，为了能够控制该参数，再利用xi(t-τ +β)≈r1xi(t-τ)+r2β x˙i(t-τ)和 vi(t-τ+β)≈r1vi(t-τ)+r2β v˙i(t-τ)，可得到具有时滞状态导数反馈的一致性协议

该协议中 β ≥0表示时滞状态导数的反馈强度，权重系数 r1,r2＞0 。当r1=r2=1 且 β =0时，该协议式(2)变为传统的一致性协议。对于2阶多智能体系统，如何提高系统的时滞鲁棒性是一个十分重要的问题，目前，在不改变网络拓扑结构的情况下，可以通过减少网络的连通性来解决该问题，但是由于减少连通性会降低多智能体系统实现一致收敛的速度，为了克服两者之间的矛盾，文献[15,16]引入时滞状态导数反馈协议部分解决了该问题。然而，如果反馈强度过大，系统在任意通讯时滞下都会发生震荡[17]，这需要寻求新的方法来解决。随后，Wu等人[18]设计了一种加权平均预测的一致性协议，在该协议下，问题得到了解决，但是该协议结构需要利用积分理论做加权平均处理，导致结构过于复杂，在实际应用中很难实现。本文将采用一种相对简单的加权方法，给出一种新的具有加权项的时滞状态导数反馈协议式(2)，分析系统式(1)的一致性和鲁棒性，此时2阶多智能体系统具有如下闭环形式

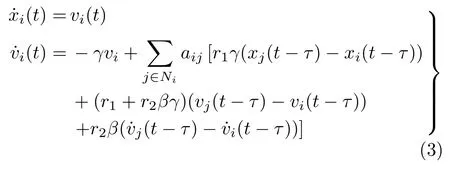
本文的创新之处在于提出了一种具有加权项的时滞状态导数反馈协议，在定向通讯网络拓扑下，改进了大通讯时滞导致2阶多智能体系统容易发生震荡的问题。下面将采用频域理论研究系统式(3)的一致性和鲁棒性。

2 主要定理

2阶多智能体系统的一致性要求位置与速度都要达到一致，具体定义为

而且当通讯时滞 τ =τmax时，系统式(3)的解必定全局震荡。

由于矩阵 L 为 N 阶方阵，所有s =-γ是上面特征方程的 N重根，为了使系统式(3)实现渐近稳态一致，需要研究方程

注：定理1表明对于所有权重系数 r1,r2＞0，只要反馈强度 β和通讯时滞τ 满足一定的条件，就可以保证系统式(3)渐近实现稳态一致。然而为了确保具有时滞状态导数反馈的一致协议能够更加准确地反映传统一致性协议的性能，在实际应用过程中，往往需要对参数 r1,r2和β 进行约束。一般地，r1和 r2越接近1，且β 越接近0，对传统协议的性能反映越准确。当β =0时，协议式(2)变为传统的一致性协议，下面考虑协议式(2)比传统的一致性协议更有优势，为了证明该问题，只要找到恰当的β 使得τmax|β/=0＞τmax|β=0即可。

3 数值仿真

在 β=0 和r1=r2=1 下，取τ =1.3，系统式(3)的位置和速度状态变化趋势见图1。这里的横坐标时间概念表示多智能体系统中xi(t) 和vi(t)的时间变量t，纵坐标表示两者的数值。

从图1可以看出，此时2阶多智能体系统发生明显的震荡，主要原因在于此时的通讯时滞τ =1.3 ＞τ∗，系统式(3)会发生震荡，从而定理结论有效。

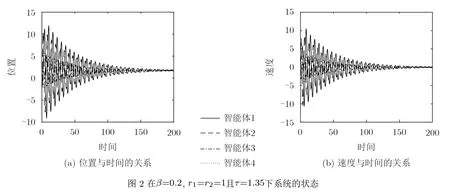
另外，当β =0.2且 r1=r2=1时 ，取通讯时滞τ =1.35，系统式(3)的位置和速度状态变化趋势见图2。

从图2可知，尽管τ 增加到1.35，但是系统式(3)却能够渐近实现稳态一致。这是因为此时 β调整为0.2时，使得τ =1.35 ＜τmax=1.4051，从而系统式(3)能够渐近实现稳态一致，于是定理结论有效。

最后，保持反馈强度β =0.2不变，将权重系数调整为 r1=0.9和 r1=0.8 ， 此时在通讯时滞τ =1.5下，该系统的位置和速度状态变化趋势见图3。

从图3可知，即使将通讯时滞增大到τ=1.5 ＜τmax=1.5484，在给定的权重参数下，系统式(3)仍能够渐近实现稳态一致。结合图1-图3，尽管时滞从1.3增加到了1.5，但是只要给定适当 β , r1和 r2，即可 保证系统式(3)渐近实现稳态一致。

4 结论

研究表明，对于在定向网络拓扑结构下2阶智能体系统，具有加权项的时滞状态导数反馈协议有较大的优势，它们比传统的一致性协议能够容忍更大的通讯时滞，而且该协议中的参数调整相对简单，比较容易实现。对于系统的通讯时滞偏大的情况，系统往往会发生震荡，为了解决震荡问题，只要引入具有加权项的时滞状态导数反馈协议，通过对反馈强度和权重系数进行调整，即可保证系统渐近实现稳态一致。