语义分割网络重建单视图遥感影像数字表面模型

卢俊言 贾宏光* 高 放 李文涛 陆 晴

①(中国科学院长春光学精密机械与物理研究所 长春 130033)

②(中国科学院大学 北京 100049)

③(长光卫星技术有限公司 长春 130102)

1 引言

遥感影像的数字表面模型(Digital Surface Model,DSM) 是在数字高程模型(Digital Elevation Model,DEM)的基础上，进一步包含了地面上的建筑、道路桥梁，以及树木植被等地物高度的模型，在许多基于遥感场景的问题研究中有重要应用，例如城市遥感影像的语义标注[1]、变化检测等[2,3]。

当前，DSM的获取主要是通过机载激光雷达的激光探测与测量(Light Detection And Ranging,LiDAR)数据，因此主要存在两个获取难点：第一，昂贵的时间、设备和人力成本；第二，由于发展、变迁等导致的历史影像数据的DSM无法获得。此外，当前技术多通过立体摄影测量方法(例如空中三角测量等)，基于多视图(multi-view)影像建立DSM，而仅通过单视图(single-view)影像建立DSM鲜有成熟的方法论，主要原因是该问题属于不适定问题(ill-posed problem)[4]。

近年来随着深度学习技术的发展，其在图像处理领域中很多不适定问题的求解上表现出了卓越的效果，例如图像修复[5]，图像超分辨率重建等[6,7]。本文研究的DSM重建问题本质上是遥感影像的高度预测(height prediction)，与其相似的一类问题是图像的深度估计(depth estimation)，二者的对比如图1所示。图1中(a)和(b)分别表示常规图像与其深度标签(来自NYU Depth V2数据集)，(c)和(d)分别表示遥感影像与其DSM数据。

在基于深度学习卷积神经网络(Convolutional Neural Networks, CNN)的单视图影像深度估计和高度预测方法上，国内外学者进行了一些相关研究。例如，EigeN等人[8]采用了两个CNN组合实现了单视图影像的深度估计，其中一个CNN用于全局深度结构的回归分析，另一个CNN用于图像分辨率的提升；EigeN等人[9]在后续研究中，又提出了结合语义标注和表面法向量的多尺度CNN结构，在深度估计的细粒度上达到了更好的效果；Liu等人[10]将CNN与条件随机场(Conditional Random Field, CRF)算法进行结合，在超像素分割的基础上采用CNN学习并提取图像特征，实现了单视图影像的深度估计；Srivastava等人[11]提出了一种将语义分割误差和高度预测误差进行线性结合的损失函数用于CNN模型训练，实现了单视图影像的高度预测。

然而上述方法对于本文的研究对象而言适用性较差或存在一定的缺陷。首先，文献[8,10]当中采用的是深度估计的方法，其研究对象是室内或室外的常规影像，而本文的研究对象是遥感影像，二者存在很大的差异，一方面遥感影像大多为正射影像，其目标的上下文信息非常有限，以至于表面法向量和条件随机场等方法不再适用；另一方面遥感影像的覆盖范围广、分辨率相对较低、地物复杂程度很高，因此结构较为简单的CNN难以有效提取到遥感影像中复杂的语义信息。其次，文献[11]采用的高度预测方法依赖于遥感影像的语义标注，然而人工语义标注的成本极高，因此该方法的实现和大规模应用较为困难，而相比之下无人机LiDAR数据的获取更加经济和便捷。

图1 深度估计与高度预测

综上所述，本文旨在实现一种仅依靠LiDAR数据，基于深度学习的语义分割技术重建单视图遥感影像DSM的方法，并实现端到端的输出。

2 基本原理

2.1 任务描述

本文旨在实现针对单视图遥感影像的DSM重建，即像素级的高度值预测。假设 ( x,y)分别代表遥感影像与其对应的DSM数据，并假设其联合概率分布为p (x,y)，本文的任务可描述为建立一个映射f :x →y，使得如式(1)的目标函数最小化

式中， f (x)表示遥感影像经过映射得到的DSM预测数据； y表示遥感影像的DSM真实数据；l (·)表示损失函数，即评估预测值f (x) 与 真值y 差距的函数；Ex,y表 示在联合概率分布p (x,y)下的数学期望。

像素级高度预测任务可以借鉴像素级图像分类任务(语义分割任务)的基本思路，区别在于后者是一个分类问题，而前者是一个回归问题。假设映射f可以通过一个语义分割模型实现，模型的参数为Θ，当给定了遥感影像与其DSM数据的样本集{xi,yi}， 可以通过学习优化获得一组最优参数Θ ˆ，使得式(1)的目标函数最小化，即

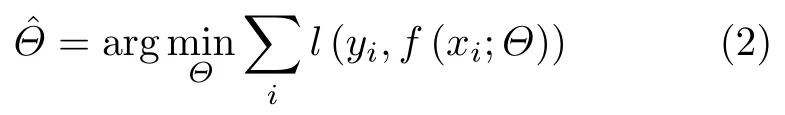
2.2 多尺度残差融合编码-解码的语义分割网络

一些关于CNN原理以及特征图(feature map)可视化的研究表明[12,13]，CNN模型的浅层网络用于提取图像局部的、低级的细节特征，例如边、角、轮廓等；深层网络用于提取图像全局的、高级的、辨识度强的语义特征。因此对于传统编码-解码结构的深度学习语义分割模型，例如全卷积网络(Fully Convolutional Networks, FCN)[14]而言，浅层特征图包含更多的图像细节特征(边缘、纹理等)，但语义信息较弱；深层的特征图包含了更多的语义信息，但损失了图像的细节特征。此外，编码的下采样过程也丢弃了像素的位置信息，宏观上像素位置信息又组成了图像的结构信息。在解码过程中虽然将编码后的特征图重新上采样，但上采样属于一个不适定问题，因此原始图像的细节特征和结构信息都无法真正恢复。杨宏宇等人[15]在一项利用深度卷积神经网络进行气象雷达噪声图像语义分割的研究成果中，采用了一种将图像高维全局语义信息与局部细节特征融合的方法来提高分割精度，为上采样的细节损失问题提供了一种解决思路。

综上并基于任务描述，本文提出了一种多尺度残差融合编码-解码(Multi-scale Residual Fusion Encode-Decode, MRFED)的语义分割网络，网络结构如图2所示。在编码部分，遥感影像输入MRFED后经过一系列编码块(encode block)逐步提取图像特征，得到高维度的特征图(特征图#5)，其中包含了图像的全局语义信息，语义信息中又包含了高度信息，特征图#5的分辨率较低；在解码部分，特征图#5经过一系列解码块(decode block)逐步恢复至原图尺寸，通过回归运算最终实现像素级的高度预测，得到DSM预测数据。为了解决输入图像细节特征和结构信息丢失的问题，MRFED采用了一种跳跃级联(skip connections)的策略，将编码过程中的浅层特征图直接复制拼接(copy & concatenate)到解码过程中相同分辨率的深层特征图上，继而进行后续传播。一方面，该策略使输出结果保留了原始图像的细节特征和结构信息；另一方面，使用该策略后的网络模型参数量仅增加了约0.7‰(原参数量约为1.2e+08，增加了约8.4e+04)，增加的运算代价微乎其微。

舒曼是学面案的。他认为这种专业可以一辈子饿不着。舒曼和那个一蹶不振的艺术家在一起生活的时候就经常挨饿。于是，舒曼毫不犹豫地选择了“吃”这个专业。就舒曼的艺术才能而言，他完全可以报考一家艺术院校，他的小提琴拉得也不错。但他没那么做。

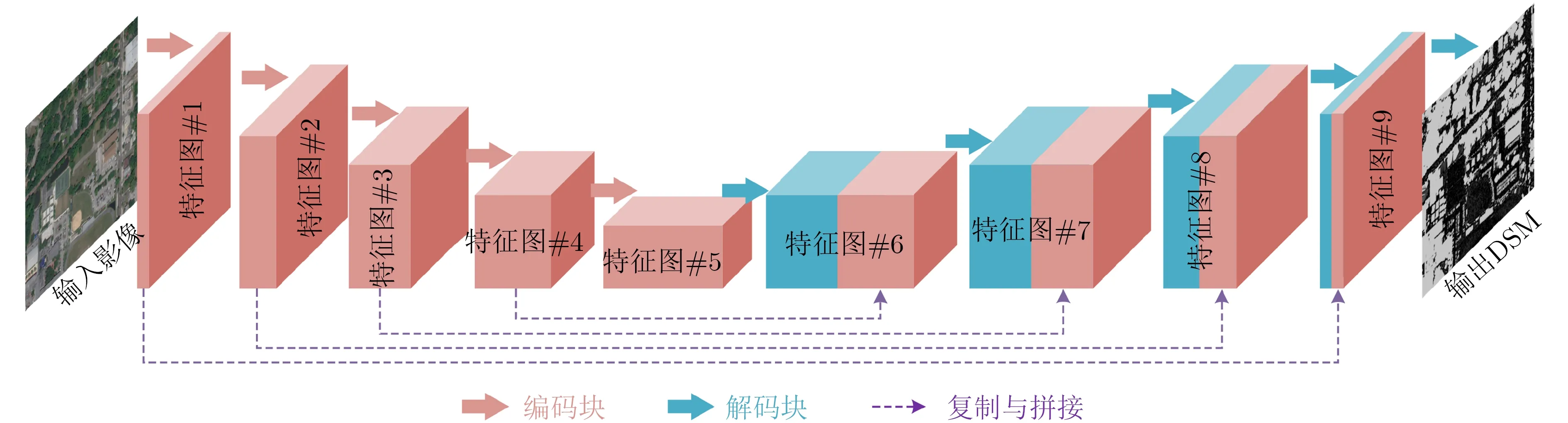
图2 MRFED网络结构示意图

He等人[16]提出的残差融合(residual fusion)方法有效解决了卷积神经网络随着深度增加而出现的退化问题。罗会兰等[17]的研究结果表明，在语义分割方法中使用多尺度提取相互重叠的区域，能够得到更加精细的物体分割边界，证实了多尺度的特征融合能够提高语义分割的精度。因此，基于Res-Net的残差融合思想，本文提出了一种多尺度残差融合的编码块与解码块单元，结构如图3所示。图中 Ki表 示 N 个级联的3 ×3 卷 积核，当i =2,3,4时，对应的 N =1,2,3，级联的卷积核越多，输出结果的感受野(receptive field)越大，即对应了原图像不同尺度的特征提取结果。编解码块将多尺度的特征提取结果相叠加，再进行类似瓶颈块的残差融合，具体过程如下：在编码块中，输入首先经过1 ×1的卷积层改变通道数(channels)，得到的特征图按通道数平均分为4部分，记为 x1∼x4; Ki的卷积操作不改变输入 xi的尺寸和通道数，对应的输出为y1∼y4,xi与yi的关系如式(3)所示

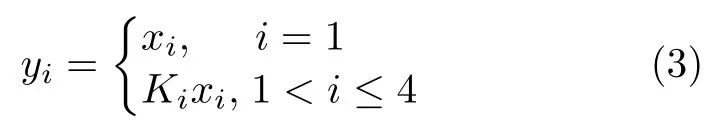
将y1∼y4进行拼接(concatenation)，再经过一个 1 ×1，步长为2的卷积层，输出特征图的尺寸为输入的1/2，通道数为输入的2倍；最后，将整个编码块的输入经过同上的卷积层，结果与前者的输出按位相加(element-wise addition)，即残差融合，得到整个编码块的输出。解码块的结构与编码块基本一致，唯一的不同是将编码块的下采样操作变为上采样。解码块采用了反卷积(deconvolution)[18]进行上采样操作，通过选择合适的膨胀率(dilation rate)和补零策略(padding)，即可输出目标尺寸的特征图。本文设计的编解码块在ResNet瓶颈块的基础上增加了模型复杂度，但仅增加了很少的参数量和运算量(相比ResNet-50而言，其原本的参数量约为4.6e+07，本文的编解码块增加了约6.0e+05参数，增量约为1.3%)。上述的编解码块具备下采样和上采样功能，但除此之外，MRFED中还存在一部分编解码块，只对输入进行特征提取，而不改变输入的尺寸，此类编解码块的结构与上述基本一致，只是用于上下采样的卷积层改为等尺寸输出，因此不再单独描述。整个网络的特征图尺寸和通道数信息如表1所示。

3 实验与结果

3.1 实验样本生成

本文采用的训练数据集来自IEEE GRSS(Geoscience and Remote Sensing Society)提供的一个公开数据集，该数据集包含2783张单视图多期遥感影像，影像尺寸均为 1024×1024, RGB三通道，成像地点是美国的两座城市：佛罗里达州的杰克逊维尔(Jacksonville, Florida)，以及内布拉斯加州的奥马哈(Omaha, Nebraska)；影像数据由Digital Globe公司的worldview系列卫星拍摄，地面采样间隔(Ground Sampling Distance, GSD)为0.35 mpp(m per pixel)；影像的DSM数据由LiDAR获取。

MRFED默认的输入尺寸为5 12×512，因此首先将原数据集的图片和DSM进行裁剪，然后再进行数据增量操作。本文采用的数据增量方法均为无损变换，即不增加或者损失图片的任何信息，主要包括：

(1) 随机水平或竖直翻转；

(2) 随机旋转90°；

(3) 随机x-y坐标轴转置。

3.2 损失函数设计、模型初始化方法与超参数选取

本文的实验基于Keras深度学习框架实现了算法模型。

(1) 损失函数设计：实验时分别采用了平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Squared Error, RMSE)作为损失函数，二者的公式如式(4)和式(5)所示

图3 编码块与解码块结构

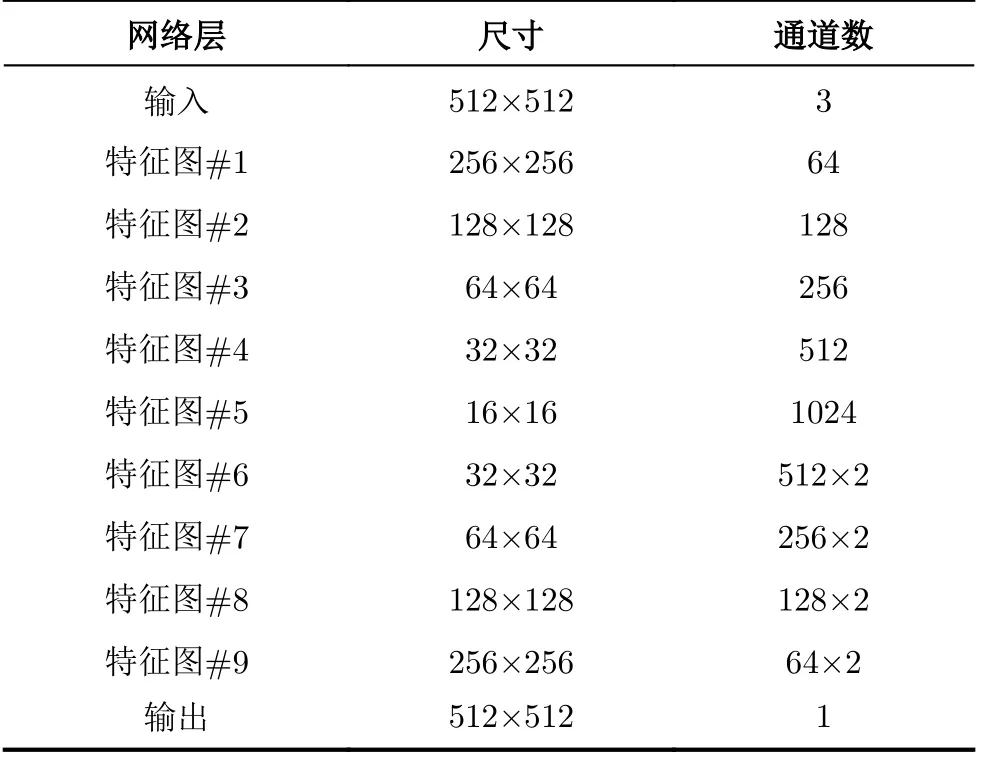
表1 MRFED各层的特征图尺寸和通道数信息

式中， yi表示真值，y ˆi表示预测值；实验结果表明采用MAE作为损失函数的效果略好，训练迭代相同次数的情况下，模型的测试精度高于RMSE约2.4%。

(3) 超参数(hyper parameters)选取：实验采用Adam算法[20]作为梯度下降的优化算法，其中的超参数均选用算法推荐的默认值，分别为：β1=0.9,β2=0.999, ε =1e-08 , η =0.0001；训练每次迭代的BatchSize设为1，迭代次数设为1e+06(训练过程中视收敛情况手动停止)；本实验的GPU设备采用NVIDIA GeForce GTX TITAN X (算力6.1 TFLOPs，显 存12 GB)，训练时长约为60 h。

3.3 实验结果

MRFED在测试集上的DSM重建效果如图4所示。图4中(a1)-(a4)分别为测试集中包含密集建筑物、大面积高植被、承重高架桥和大面积水域的遥感影像；(b1)-(b4)分别为(a1)-(a4)的DSM真值热力图；(c1)-(c4)分别为(a1)-(a4)的DSM重建结果热力图；热力图中蓝绿色表示高度值较小，橙红色表示高度值较大。从图4中可以看出，DSM重建结果与真值的数据范围基本一致，多种地物类型的高度预测结果都较为准确，热力图的相似性尤其是结构相似性很高。

在数据指标方面，本文采用测试集上DSM真值和测试结果的MAE, RMSE和SSIM来评价DSM重建效果。其中结构相似性 (Structural SIMilarity,SSIM)是衡量两张图片结构相似性的指标，如式(6)所示

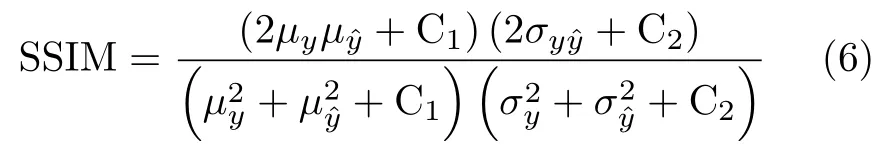
式中， µy和 µyˆ表 示y 和y ˆ 的 均值，σy和σyˆ表 示y 和y ˆ的标 准 差， σyyˆ表 示y 和y ˆ 的 协 方 差，C1和C2为 常 数，其中C1=6.5025, C2=58.5225。

本文选取了两个经典的语义分割模型与MRFED进行纵向对比实验，分别是FCN和U-net[21]，其中FCN的主干网络(backbone)采用VGG16, U-net的主干网络采用ResNet-50，针对本文的任务对二者进行了如下修改：将二者最后一个用于分类的激活层去掉(Softmax或Sigmoid)，增加一个输出维度为1的全连接层用于回归运算，以输出高度预测值。FCN, U-net与MRFED在测试集上(共1670个样本)的实验结果数据指标如表2所示，三者的MAE, RMSE和SSIM实验结果曲线如图5所示。从测试结果可知，MRFED的DSM重建效果明显优于经典的语义分割网络FCN和U-net；其中FCN采用了没有残差融合结构的VGG16作为主干网络，编码阶段提取语义特征的能力较弱，因而结果较差；U-net采用了具有残差融合结构的ResNet-50作为主干网络，能够较为有效地提取语义特征，因而结果得到了明显提升；MRFED在残差融合的基础上又增加了多尺度的设计，使得编码阶段得到了更好的语义特征提取效果，同时表2中关于跳跃级联的消融实验(ablation study)结果，证实了解码阶段采用该策略能够有效提高精度，并显著提高结果与真值的结构相似性。MRFED在测试集上最终取得了MAE为2.1e-02, RMSE为3.8e-02, SSIM为92.89%的实验结果，实现了高精度的DSM重建，并且有效保留了原始图像的细节特征和结构信息。

本文还与文献[11]中所提方法ST loss进行了横向对比实验。文献[11]中的实验采用了国际摄影测量与遥感协会(International Society for Photogrammetry and Remote Sensing, ISPRS)提供的一个公开数据集Vaihingen，本文将MRFED在该数据集上进行了训练和测试，具体细节上：Vaihingen数据集中共有16幅影像带有DSM标注，选取其中的12幅为训练集，4幅为测试集；影像的平均像素尺寸约为2500 × 2000，采用与3.1节中相同的方法对影像进行裁剪和数据增强，最终得到的训练集共包含1260个5 12×512的RGB与DSM影像对，测试集包含420个RGB与DSM影像对。MRFED在该数据集上训练后取得了优于文献[11]的DSM重建结果 ，如表3所示。

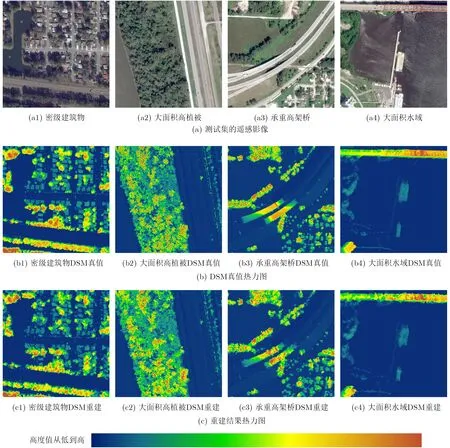
图4 MRFE的DSM重建结果

表2 测试结果的数据指标

4 结论

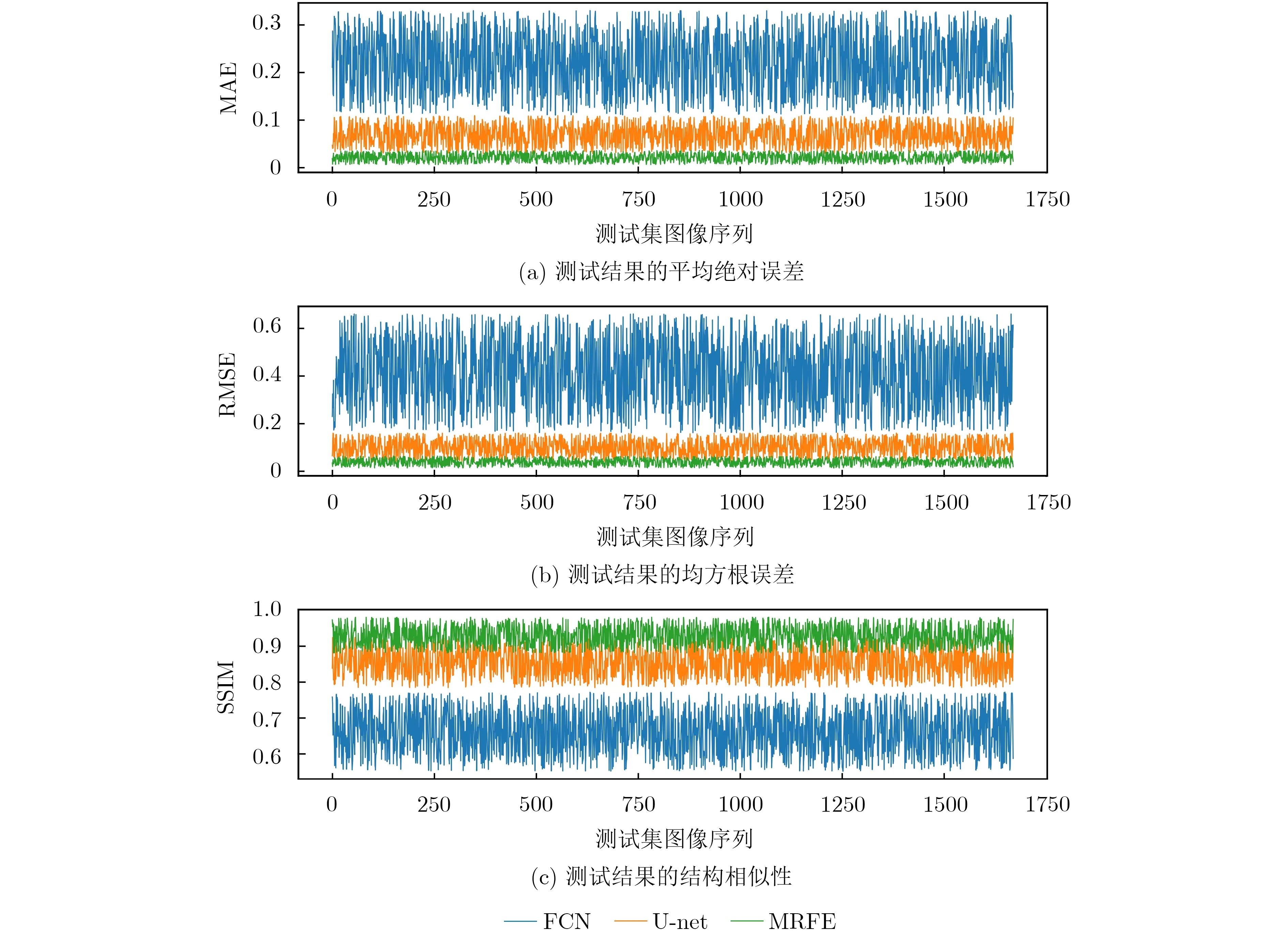
图5 测试结果的数据指标

表3 Vaihingen数据集上的DSM重建结果对比

在单视图遥感影像的3维重建技术还并不成熟的研究现状下，本文提出了一种新颖的基于深度学习技术的单视图遥感影像DSM重建方法。本方法设计了一种多尺度残差融合编码-解码的语义分割网络--MRFED，在编码阶段，通过多尺度残差融合的CNN实现了遥感影像中复杂语义信息的有效提取，进而回归得到高精度的高度预测值；在解码阶段，采用特征图跳跃级联的策略保留了输入图像的细节特征和结构信息。本方法的实现仅依赖于遥感影像及其DSM数据，无需遥感影像的语义标签，因而节省了昂贵的人工语义标注成本；本方法实现了端到端的输出，在公开数据集上进行了测试， DSM重建结果与真值的MAE为2.1e-02, RMSE为3.8e-02, SSIM为92.89%，实验证实本方法能够有效实现单视图遥感影像的DSM重建，具有较高的精度和较强的地物分布结构重建能力。