基于历史梯度平均方差缩减的协同参数更新方法

谢 涛 张春炯 徐永健

①(西南大学教育学部智慧教育研究院 重庆 400715)

②(同济大学电子与信息工程学院 上海 201804)

③(西南大学计算机与信息科学学院 重庆 400715)

1 引言

机器学习被广泛应用于图像检索、语义识别和文本信息处理，在智慧医疗、智慧城市和智慧教育等领域发挥着重要作用。许多机器学习算法的目标函数可以通过优化问题来表示，并采用随机梯度下降算法(Stochastic Gradient Descent, SGD)进行求解[1]。但是，局部梯度与全局平均梯度之间存在方差，会使机器学习算法中损失函数的收敛速度减慢。而且，SGD在目标函数强凸且步长递减的情况下次线性收敛，导致模型训练不稳定。

近年来，分布式机器学习取得了重要进展。分布式集群的节点分为参数服务器和工作节点。工作节点从服务器中提取参数，梯度的计算由工作节点进行，更新后的参数将推送到服务器，并在服务器上聚合以更新全局参数，最后与工作节点共享[2]。其模型训练主要分为同步和异步两种方式。在同步方式中，所有工作节点都需要同步消息，并在服务器更新前进行汇总；而异步方式中，服务器在一次更新迭代轮次中接收到率先计算完成的工作节点的模型参数时，不再等待其他工作节点的消息就将其更新为全局模型参数，然后分发给每个工作节点进行下一轮次迭代更新。

基于传统参数服务器和工作节点关系的SSP(Stale Synchronous Parallel)方法[3]在本地维护一个缓存参数池，每个工作节点可以直接从其中提取参数，并对参数服务器之间的同步进行额外处理，其缺点在于性能差的节点可能得不到及时发现。因此，使系统不被低性能节点影响的FSSP模型[4]和可动态决定节点失效阈值的DSSP模型[5]被提出。在这些模型中，节点间的通信要么采用自适应学习率来提高异步SGD的鲁棒性[6,7]，要么基于参数服务器系统采用类似SSP的异步通信协议进行跨节点参数更新[8]。然而，由于学习率随着迭代而衰减，导致算法的收敛速度减慢，容易出现过拟合。针对此，结合延迟近端梯度和随机方差缩减梯度的快速分布式SGD[9]使用固定学习率来保证线性收敛，性能优于传统的SGD。

由于集群中分布式机器学习的参数快速增长、同步的成本高，大大减慢分布式学习的速度。充分因子广播(SFB)计算模型被提出用于大规模矩阵参数化模型的分布式学习[10]。该方法通过在工作节点之间广播SF并在每个本地节点重构和更新参数矩阵，可提高通信效率。此外，文献[11]提出一种有效的小批量训练机制，可以加速集群中的SGD；文献[12]提出可提升训练效率的误差补偿式随机梯度下降算法，通过量化局部梯度来降低通信开销，并加快收敛速度。但这些算法主要在分布式通信机制上采用随机梯度下降算法，很少有研究兼顾考虑历史梯度的方差。

事实上，近年关于方差缩减的研究并不少见，例如SAG[13], SAGA[14], S2GD, SVRG++和Prox-SVRG[8,9,15]等。这些研究主要对模型的结构进行适当的时空折中，从而减少随机梯度引起的方差，有助于获得线性收敛速度。但大多数算法是在中心服务器上实现的，难以满足大规模分布式应用的要求。随着基于方差缩减的分布式SGD得到广泛关注，Wang等人[16]提出有效融合异步并行机制和方差缩减方法的Async-ProxSCVR算法，Ferranti等人[17]提出基于方差缩减的随机交替最小化算法SVR-AMA，均可解决对于强凸和一般非凸情况下的快速收敛问题。然而，大量算法主要使用闭环方式为节点中的多个线程(而非多个独立节点)并行更新参数。其缺点是当训练数据或参数的数量很大、不能存储在单个节点中时，模型收敛效率会受到严重影响。

鉴于此，本文的主要贡献在于采用方差缩减SGD完成分布式集群中的大规模机器学习任务，主要集中解决两个关键问题：(1)将数据分块并分配给多个工作节点后的算法“快速收敛”问题；(2)在异步通信方式下，执行全局参数分发时因快节点等待慢节点导致的“更新滞后”问题。因此，本文提出一种基于历史梯度平均方差缩减的分布式SGD(DisSAGD)，利用历史迭代的梯度方差，修正每次迭代的梯度估计，不需要完全的梯度计算或额外的存储，而是通过异步通信协议来共享跨节点参数，并在分布式集群中使用方差缩减来训练机器学习模型。

2 本文提出的DisSAGD方法

2.1 方差缩减

尽管此方法可以避免一些算法[14]存在的“无遍历迭代算法”额外存储的需求，但是需要在每次迭代时对整个数据集进行梯度估计，造成昂贵的计算代价。为了解决此问题并获得加速计算，本文在每次迭代上累积平均梯度向量，然后使用该向量进行下次迭代的梯度求解，从而避免在整个数据集上迭代循环。这些累积的平均梯度向量在机器学习算法运行时不会产生其他明显的开销。在每次估计梯度时用历史梯度来做修正，在一段时间内使用t×m个样本，经过 t轮迭代后重新选择 m个样本进行梯度计算。基于平均梯度向量方差缩减的参数更新规则如式(3)

表1 基于历史梯度平均方差缩减算法

2.2 分布式实现

本研究中，机器学习集群是基于分布式tensorflow框架实现的，集群节点划分为服务器(节点)和工作节点。工作节点从服务器中提取参数，梯度的基础计算由工作节点进行。工作节点的任何更新将推送到服务器，并在服务器上聚合成全局参数。最后，这些新的全局参数将与工作节点共享。考虑到方差缩减随机梯度主要是通过数据驱动模型收敛，本文采用数据并行，而非模型并行。通过数据并行，数据集 D被划分为互不相交的子集，将每一个子集指定到工作节点p, p ∈{1,2,···,P}。 令Dp为第p个数据划分。可得到数据并行的更新公式为

其中， t 表示迭代轮次，W 表示模型状态，△ (·)表示更新函数，它独立地运行在数据集 Dp上，最后将各工作节点的中间梯度结果通过F (·)进行汇总以更新全局梯度。值得注意的是，在数据并行方式中，假设数据集是独立同分布的，且每一个工作节点的执行能力都相等。工作节点将计算结果传输到分布式网络之前，△ (·)先在本地CPU上运行，因此在配置相同的工作节点上，△ (·)在单个节点的计算延迟可以忽略。

另一方面，工作节点以异步方式执行机器学习任务，通过gRPC消息传递从服务器中提取参数 ω，并开始机器学习模型的迭代计算。在每次迭代中，工作节点首先从训练数据中随机选择一个样本，然后使用式(1)计算梯度。在迭代过程中，所有工作节点相互独立。当迭代完成时，工作节点将此轮迭代训练好的机器学习模型参数ω 推送到服务器。

假设数据分布在p 个工作节点上，这些工作节点只能与对应的服务器通信，拓扑如图1所示。将数据索引集 {1,2,···,n} 分 解为不相交的子集{ψs}，每个 ψs表 示存储在服务器s 上的数据索引。目标函数由式(5)给出。

本文方差缩减方法容易实现以异步方式分发，因为它不涉及像SVRG那样计算目标函数的完整梯度。此外，由于算法仅需要在每次迭代结束时更新梯度的平均值，因此可以增加服务器和工作节点之间的通信时段，从而保证机器学习模型快速且稳定的收敛。

综上所述，本文提出的DisSAGD算法伪代码如表2所示。具体执行过程如下：先启动服务器创建分布式集群，再启动主工作节点，协调其余工作节点的初始化和同步等待问题(第(1)行)。工作节点由gRPC传递模型参数。一旦工作节点从服务器接收到消息，它就会从服务器中提取全局参数，并开始迭代过程(第(2)行)。对于所有工作节点都会调用表1中的程序，实现本地参数更新(第(3)0～(5)行)。当工作节点从训练数据中随机采样时，它使用缓存的本地梯度更新参数(第(6)～(9)行)，最后将新学习的参数推送至服务器，汇聚成新的全局参数(第(10)行)。DisSAGD算法有效地利用了历史梯度缩减方差，与文献[2,3]提到的Petuum SGD算法和文献[6]提到的Downpour SGD算法不同的是：它可以快速收敛而不会在迭代期间衰减学习速率。

2.3 具有加速因子的学习率

方差缩减技术一般使用恒定的学习速率来加速机器学习算法。虽然恒定学习率对于L-平滑和γ-强凸目标函数表现良好[18]，但是还可以利用一些内在属性来加速机器学习算法的收敛[19]。因此，本研究引入加速因子σ 指导DisSAGD的学习率变化，如式(6)所示。

2.4 自适应采样

由于DisSAGD的工作节点每次迭代需要使用采样策略进行模型训练，因此确定每次迭代中随机采样多少样本非常重要。在表1算法中，如果 m被设置为较大的值，就需要在迭代期间花费很多时间更新本地参数；相反，如果 m值较小，DisSAGD必须进行额外的迭代次数以降低损失函数。在集群中，尽管异步通信允许延迟，但是当超过允许的延迟范围，同次迭代中训练速度快的工作节点必须等待慢速的工作节点，即产生“更新滞后”问题，大大地增加了DisSAGD的收敛时间。

为了解决这一问题，本文在表2算法中采用一种自适应动态采样策略，动态调整 m。当一个工作节点比其他工作节点更快时，它将为下一次迭代采样更多样本，这将使更快的工作节点有更多时间来计算局部梯度。因此，慢速的工作节点有机会赶上快速工作节点，并且等待时间显著减少。每次迭代完成时，训练的新本地参数将被推送到服务器，服务器将检查所有工作节点是否获取全局参数。如果工作节点训练完成太快，则需要等待其他慢速工作节点。快速工作节点将 m 调大为m +δ, δ是非负整数。为方便起见，令 δ =0.05m。这样，训练速度快的工作节点每次对更多的训练样本进行采样，同时 等待慢工作节点。

图1 分布式机器学习拓扑

表2 DisSAGD算法的伪代码

3 性能测试

测试分为两部分。首先，实验对具有加速因子的学习率在独立的工作节点上运行线性回归任务。数据集采用由谷歌开源的街景门牌号码SVHN[3]，它是做线性回归任务的经典数据集。机器学习模型使用Alexnet[14]，每个网络层使用Mish[15]作为激活函数。然后，实验在集群环境中对另外两个数据集分别使用异常检测问题和分类问题来评估Dis-SAGD的性能。评估指标有收敛性、加速效果和平均等待时间。

异常检测问题的损失函数模型如式(7)所示

其中， x 是训练数据，y 是机器模型的输出值，N 是训练数据的大小。机器学习模型使用Resnet18[16]，激活函数也是Mish。数据集采用KDDcup99，它被认为是异常检测问题的经典数据集，包含463, 715个样本，每个样本有41个维度。

分类问题的损失函数模型如式(8)所示

同样， x 是训练数据，y 是机器模型的输出值，N是训练数据的大小。机器学习模型使用Autoencoder[17]，激活函数使用Mish。数据集采用具有代表性的Cifar-100[9]。它由60000张大小为32×32的三通道彩色图像组成，分为20个大类，每个大类包含5个小类，总共100个小类。每个小类包含600张图像，其中500张用于训练，100张用于测试。

本实验在星环超融合大数据一体机集群上进行评估测试。该一体机共有32个计算节点，每个节点配备了两个1536核CPU。m设定为1024，分布式实现使用第三方开源分布式机器学习系统tensorflow来进行性能评估。实验采用异步通信，延迟设置为0.5 s，数据集分配在4个工作节点上。

本实验使用以下算法进行了机器学习模型训练性能的比较：

(1) Petuum SGD[2]：该方法是使用异步方式实现的分布式SGD，其学习率每次迭代结束时以固定因子0.95进行衰减，该代码从http://petuum.github.io/下载；

(2) SSGD：该方法是SGD中最直接的分布式实现，其主设备简单地在每次迭代中将负载分配给工作节点，确保工作节点使用相同的模型参数集执行梯度计算，该代码从https://github.com/codlife/Ssgd下载；

(3) DisSVRG[20]：改造了随机方差缩减算法SVRG，使其从原来的串行单机版算法扩展至针对大规模数据集的分布式训练算法；

(4) ASD-SVRG[21]：一种较新的分布式优化算法，使用SVRG进行自适应采样，基于历史梯度局部Lipschitz常数进行估计；

(5) DisSAGD：本文提出的未采用具有加速因子学习率和未采用自适应采样的算法；

(6) DisSAGD-tricks：本文提出的具有加速因子学习率和自适应采样的算法。

3.1 模型性能

KDDcup99的性能评价指标为 F1, F1=2PR/(P +R), P 为准确率，R 为召回率。当 F1值越大，效果越理想。Cifar100和SVHN数据集分别使用top5的准确率作为评价指标。各模型性能比较结果如表3所示。可看出：本文提出的DisSAGD实验结果比其他3种的模型性能更好，ASD-SVRG与本研究提出DisSAGD性能相当，而优化的DisSAGDtricks比DisSAGD的模型效果更优。这是由于本文考虑了历史梯度的方差，使模型训练较为稳定不会出现像使用随机样本时的振荡；而且，具有自我调节的学习率使得模型可以寻找到目标函数的鞍点，获 得最优的模型参数。

3.2 收敛效果

图2显示了具有加速因子的多个学习率在独立工作节点上的测试结果。横轴表示训练时间，纵轴为损失函数。结果显示：即使固定值部分很大，加速因子对算法的加速效果依然明显。具有加速因子的学习速率使得基础机器学习算法比没有加速因子的恒定学习速率收敛得更快。当学习率固定值部分取值较小时，机器学习模型收敛效果更显著，因此在本实验中可以设置λ =10-3。

图3显示了在分布式集群中算法的收敛效果。DisSAGD-tricks在两个数据集上的收敛性能均优于其他算法。在KDDcup99上，该算法的损失值随着时间的增加迅速下降，收敛的时间少于50 s；在Cifar100上具有类似表现。DisSAGD算法性能依赖于具体数据集，即在KDDcup99上不超过SSGD，而在Cifar100上则优于SSGD，但总体上的收敛性能好于PetuumSGD。ASD-SVRG的性能明显优于PetuumSGD和SSGD，并和DisSAGD的性能十分接近(在特定的时间二者损失函数值相等，但随着时间的增加ASD-SVRG的性能变得越来越好)；另一方面，ASD-SVRG的性能与本文提出的Dis-SAGD相当，但明显次于优化的DisSAGD(即本文的DisSAGD-tricks)算法。实验结果表明：DisSAGD采用异步方式以及基于平均梯度向量方差缩减来更新参数，具有加速因子的学习速率加速了收敛，同时自适应采样策略显著减少了服务器分发全局参数的等待时间。

表3 模型的F1值

图2 不同加速因子在独立节点运行损失函数值的变化

3.3 加速效果

通过改变分布式集群中的工作节点数量，算法的加速效果如图4所示。DisSAGD工作节点数量越多时其加速越近似线性。当使用32个工作节点时，DisSAGD在KDDcup99数据集上的加速相对于4个工作节点提高了19倍。在Cifar100数据集上使用32个工作节点时，DisSAGD可以保持接近线性的加速。这种效果主要归功于异步通信方式和方差缩减技术。异步方式使得工作节点之间相互独立，不存在滞后问题，从而减少了工作节点之间的等待时间。方差缩减技术减少了SGD的方差，并使DisSAGD以恒定速率收敛。

3.4 等待时间

图5显示了在独立工作节点上自适应采样的运行结果。在图5(a)中，调整后的m值使目标函数得到快速收敛。由于等待时间与节点数量相关，算法运行在由5个节点组成的集群中，其结果如图5(b)所示。通过改变m来评估平均等待时间。延迟设置为0.05 s。很明显，自适应采样策略减少了迭代期间的平均等待时间，这样对时间折中处理使模型训练更加精准。

图3 不同算法之间收敛性能比较

图4 DisSAGD算法中不同工作节点数量的加速效果

图5 自适应采样对收敛和等待时间影响

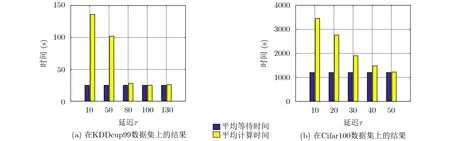
图6 不同延迟时间对平均等待时间和平均计算时间的影响

图6显示通过改变延迟τ的值，本文所提出算法的平均时间消耗。由于小延迟意味着工作节点之间的联系紧密，通常会导致快速工作节点因异步通信而等待。当延迟τ很小时，平均等待时间很长。例如，当延迟设置为0时，每次迭代中服务器需要将全局参数分发到所有工作节点，从而增加了等待时间。当延迟变大时，工作节点变得稀疏，等待时间急剧减少。因此，设定合理的通信延迟可以有效减少平均等待时间。尽管快速工作节点有更多的自由时间来进行迭代，但是慢速工作节点不能在大延迟内从服务器中获得新的全局参数，无法从快工作节点中受益。因而延迟不应该设置太小或太大，它是工作节点等待时间和计算时间之间的折中。设置的延迟应该使DisSAGD的总时间消耗达到最小。本实验中，KDDcup99数据集训练时的延迟τ应设置为200，Cifar100数据集训练时的延迟τ应设置为50。

3.5 时间差异平衡

为了研究设定多少个工作节点与服务器交互可以更好地平衡计算和等待时间的差异，本文将服务器收集到特定数量工作节点的模型参数开始进行全局参数的计算，然后在整个分布式集群中迭代，结果如图7所示。当服务器对工作节点聚合数量为2～16 h，其平均等待时间随着节点数量的增加逐渐减小、平均计算时间逐渐增大。对于3个数据集，其平均等待时间和平均计算时间在特定数量的工作节点上有交汇点。总体上，平均等待时间的下降幅度大于平均计算时间的上升幅度，说明通过指定工作节点数量的方式不如通过设置延迟时间获得的增益大。工作节点在延迟时间内可以自适应采样进行模型训练，从而达到较好的效率和收敛性能。

图7 平均等待时间和平均计算时间的平衡

4 结束语

针对将数据分配给多个工作节点后的算法收敛问题和在异步通信方式下执行全局参数分发时存在的“更新滞后”问题，本文提出了DisSAGD算法。该算法结合方差缩减技术，不需要完整数据集的梯度计算或额外的存储，并利用损失函数的凸平滑特性，使用具有加速因子的学习率进行优化。本文在迭代期间采用自适应采样策略，使慢速工作节点有机会在迭代期间赶上快速工作节点，从而减少了由滞后问题引起的等待时间。本文的局限在于：由于工作节点硬件限制，当单一节点上数据量过多时训练会出现内存溢满问题；某一节点上出现较少数据时，该节点模型不能快速收敛。