高新技术产业园区创新活动内生性与效率

丁建国 黄旭平

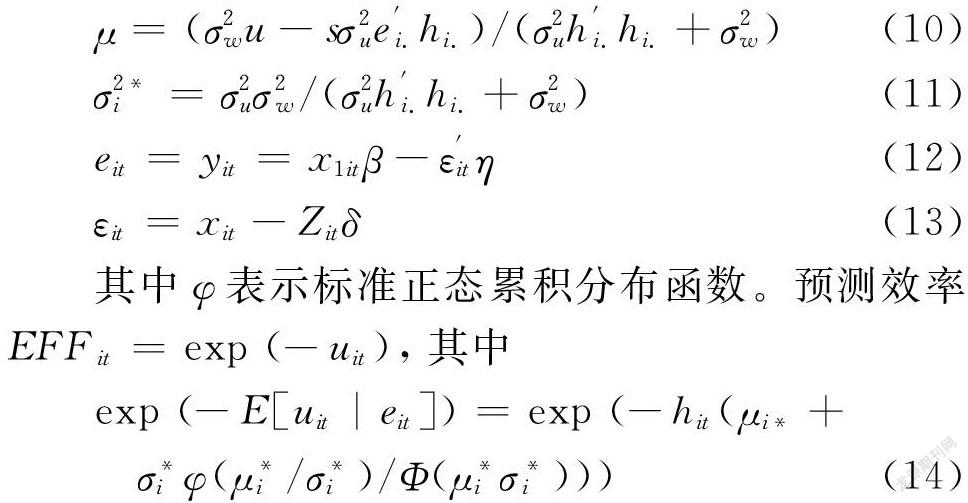
基金项目：广东省哲学社会科学规划项目（GD19CYJ18）

作者简介：丁建国（1976—），男，湖南株洲人，广西大学商学院博士研究生，研究方向：技术经济;黄旭平（1974—），男，博士，广西大学商学院副教授，研究方向：金融科技与产业创新。

摘 要：基于非平衡面板内生随机前沿模型，通过2009-2019年54个高新技术产业园区的非平衡面板数据，分析了高新技术产业园区创新活动的内生性与效率的关系。研究发现：科技经费和从业人员存在内生性，市场结构、科技经费和从业人员对创新效率有显著的正面影响;面板内生随机前沿模型可以显著地区别于外生随机前沿模型的创新效率估计。

关键词：内生性;高新技术产业园区效率; 面板内生随机前沿模型;工具变量; 地区差异性

中图分类号：F273.1 文献标识码：A 文章编号：1003-7217（2021）06-0132-07

一、引 言

自1988年我国第一个高新产业园区——北京新技术产业开发试验区建立以来，我国先后建立了168个国家级高新技术产业园区和工业园区。这些高新技术产业园区创新活动对于地区产业结构调整与升级、地方经济高质量发展以及区域竞争力提升等方面起到了重要的促进作用。然而，随着我国社会经济结构的转型升级和国际竞争力不断提升，中美贸易摩擦、國际贸易保护主义抬头等日趋复杂的外贸环境对高新技术产业园区创新效率产生了不确定性的影响。因此，如何评测高新技术产业园区创新效率，对我国高新技术产业园核心竞争力的提升与实现可持续发展具有重要意义。

已有研究主要对效率分析的内生性问题进行了探讨。例如，Shee 和 Stefanou（2015） 的研究表明传统的随机生产前沿通常低估了资本产出弹性与企业技术效率[1]。Tran 和 Tsionas（2015）在没有考虑外生工具变量的情况下，采用内生回归法估计随机前沿模型的方法研究效率分析的内生性问题[2]。Karakaplan等（2017）则提出一个基于最大似然估计方法来处理内生性问题的随机前沿模型[3]。Mutter等人（2013）考察了成本函数变量的内生因素对随机前沿分析（SFA）无效率估计的影响[4]。欧光军等人（2018） 对产业集群创新评价的研究集中在面向结果的综合能力评价方面[5]。余东华和王必好（2020）采用马尔可夫链模型研究了技术创新效率的内生性与随机波动效应，研究发现技术创新效率具有内生性且随机变动效应明显 [6]。陈军和成金华（2010） 的研究结果表明，内生创新对中国能源效率产生正面影响[7]。然而，很少有文献系统地探讨创新活动的内生机制以及创新效率的内生性问题的解决方法。

为此，本文基于非平衡面板内生随机前沿模型，探讨高新技术产业园区创新活动的内生性与效率的关系，具体分析高新技术产业园区创新活动的内生机制，以及在克服内生性基础上高新技术产业园区创新效率问题，以期对新形势下高新技术产业园区创新效率问题提供借鉴。

二、高新产业园区创新活动内生机制

（一）创新活动的协同性和邻近性引致的内生性机制

首先，创新生产活动的协同会导致研发人员和研发费用的同向变化，而研发人员和研发费用又是高新技术产业园区效率的重要影响因素，它们的关联关系容易导致解释变量之间的相关性，从而导致内生性问题。其次，地理位置的邻近性容易导致创新生产活动的空间集聚，这引致空间活动集聚的外溢效应。这种外溢效应存在的反馈机制，使得创新主体之间开展创新想法的分享、新技术的吸收和管理经验的学习，从而促进创新活动的有序开展，实现创新活动的高效运行，提高创新生产效率。

（二）创新活动的关联性和系统性引致的内生性机制

创新被认为是由几个相互关联的阶段所组成的复杂过程，包括基础研究、应用研究、产品发展、模型准备、生产、营销、产品被市场接受等环节。所有创新的子过程是相互关联的，研究与开发是创新的基础性活动，其产生的创新成果需要商业实践上的规模化应用;市场化是创新成果经济价值实现的关键环节;创新生产过程是一种相互作用的关联行为。知识流动导致新产品的诞生、新工艺开发的前向联系。同时，企业、研发机构和高校等创新主体在创新生产活动的关联阶段中构建了一个有序、共时与协同的创新生态系统，打造良好的创新氛围，有助于创新活动的有序开展。

（三）创新活动的激励政策引致的内生性机制

政策激励一直是地方高新产业园区吸引企业的重要手段，但一方面，政策激励存在同向竞争，如高新技术产业园区出台的土地优惠政策很可能导致另一个城市也出台类似激励政策。另一方面，激励政策对所有企业是一样的，可能导致偶然性投资急剧增加，高新技术产业园区效率的解释变量与随机项之间产生相关关系，进而导致内生性问题。因此，激励政策频出可能造成适得其反的负面影响，从而导致激励政策与非效率项之间存在相关性，产生内生性问题。

三、研究设计

（一）估计方法

长期以来，学者在随机前沿模型分析中忽视了内生性问题。最近，越来越多的研究开始尝试解决随机前沿模型中的内生性问题。例如，Karakaplan和Kutlu（2017a）解决横截面数据设置中的内生性问题[8]。Karakaplan等（2019）提供了一个面板数据模型，该模型可以处理两种类型的内生性，会在面板数据环境下解决内生性问题[9]。

本文基于Karakaplan和Kutlu（2017a）提出的模型，将运用面板内生随机前沿模型方法进行高新技术产业园区创新效率的估计，同时尝试着解决面板随机前沿模型内生性的问题，提供更准确的一致无偏效率估计[8]。

面板随机前沿模型如下所示：

面板内生随机前沿模型只需要一个步骤估计参数，且不需要Bootstrap方法校正标准误差。使用类似标准Durbin-Wu-Hausman检验方法通过η的联合显著性检验解释变量的内生性，如果η是联合显著，这意味着模型存在内生性;如果η没有通过联合显著性检验，则说明传统面板随机前沿函数估计分析是有效的。

（二）变量选择

（1）新产品产值（nprod）。新产品产值衡量研发成果的商业化水平，对于以研发为主的高新技术产业园区而言，产品转化效率可以准确衡量高新技术产业园区的创新产出效率。所以新产品产值能够说明创新活动的商业价值和商业化效率。

（2）新专利技术收入（nptinc）。创新活动的持续开展，必然轉化为新产品产值的增加。专利作为创新活动所产生的结果，是确保企业获取垄断利润的重要途径。

（3）市场结构（mktstr）。一般来说，市场中企业数的增加导致市场竞争加剧。因此，根据武增海和李涛（2013）的相关研究[10]，采用企业数表示市场结构。

（4）年末资产（caplyd）。资产是企业杠杆率的影响因素，资产中借款比例的增多将导致更高的杠杆率。杠杆率越高，风险越大。因此，将年末资产作为投入指标。

（5）年末负债（liabyd）。高科技的战略性和基础性使得研发周期延长，经济效益更难以立竿见影。所以负债会影响研发投入，进而影响高技术企业的效率。采用年末负债作为效率的外生影响因素。

（6）年末从业人员数（emplyd）。年末从业人员数变化与高新技术产业园区发展关联同步，也是企业生产函数的重要因素。为此，采纳年末从业人员数作为高新技术产业园区效率的投入指标。

（7）研发R&D 经费支出（rdk）。采用R&D 经费支出作为高新技术产业园区创新活动的重要投入因素。

（8）R&D 人员（rdl）。科研活动人员对高新技术产业园区的创新效率存在至关重要的作用，引用 R&D 活动人员数量作为投入指标。

（9）创汇总额（exchsum）。参与国际分工程度高更容易通过干中学和规模效应等渠道提升高新技术产业园区生产效率。本文选择创汇总额作为高新技术产业园区生产效率的控制变量。

（10）上缴税费（tax）。上缴税费反映了政府对高技术产业各行业扶持力度，影响高新技术产业发展方向。本文使用上缴税费作为控制变量。

（三）数据来源

研究数据均来源于2009-2019年《中国火炬统计年鉴》《中国高技术产业统计年鉴》和 《中国统计年鉴》。

四、实证结果分析

（一）面板外生随机前沿模型估计结果

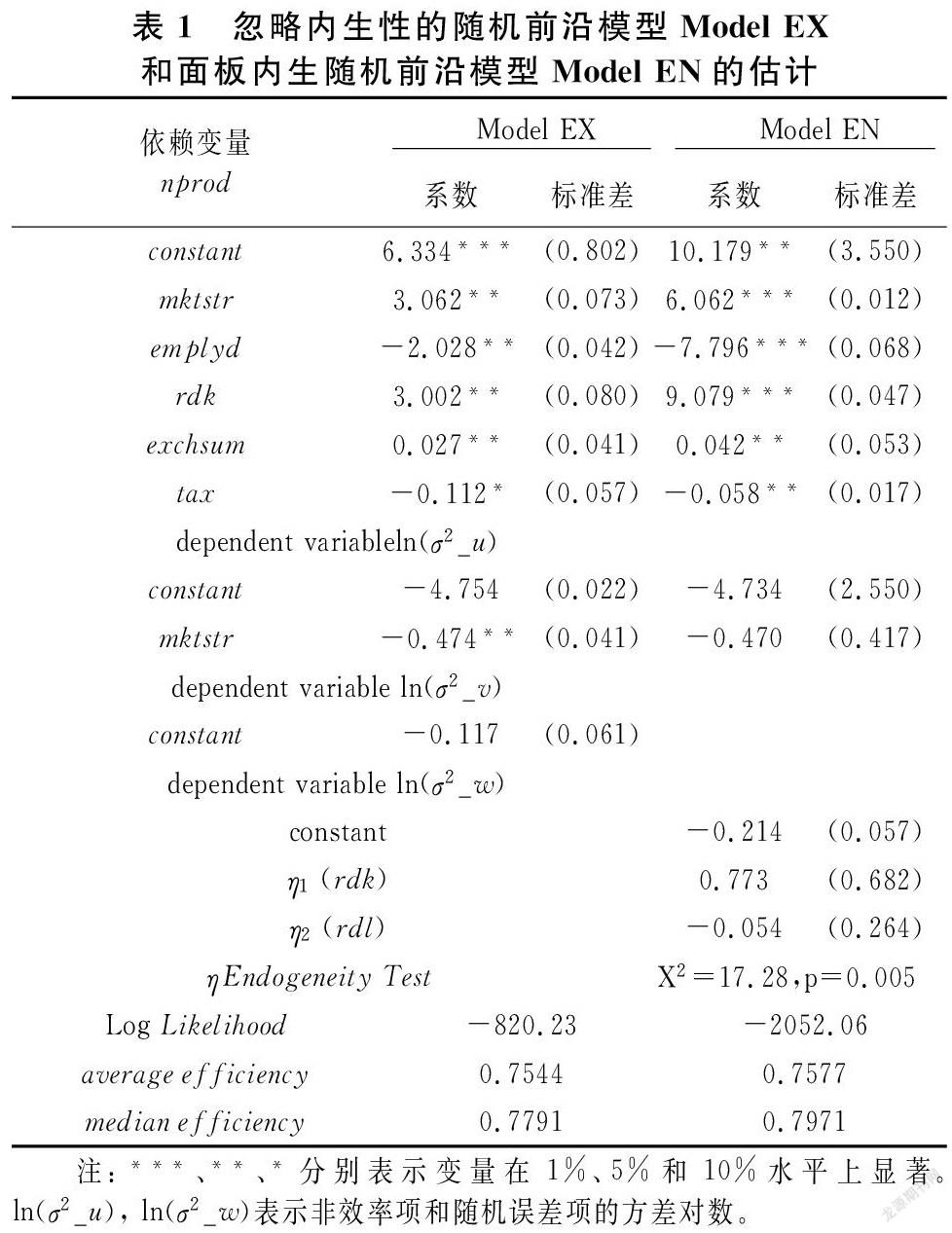
研究模型使用市场结构、科技经费、科技活动从业人数、创汇总额和上缴税额作为估计高新技术产业园区创新效率的投入变量;创新效率使用新产品产值衡量。面板外生随机前沿模型估计结果如表1所示。其中Model EX表示忽略内生性问题的面板随机前沿模型，Model EN表示面板内生随机前沿模型。Model EX结果显示：

第一，市场结构指数显著为正，统计显著性水平达到5%。这与一般理论分析不一致。一般来说，市场结构集中使企业开展竞争的积极性降低，进而导致较低的创新效率。但高新技术产业园区里的高技术企业往往是新创企业，所以市场结构与高新技术产业园区创新效率正相关，这是符合实际情况的。

第二，创新活动的两个重要指标科技经费和从业人员基本符合预期。其中，科技经费与创新效率显著正相关，显著性水平达到5%。然而从业人员与预期相反，有显著的负相关关系，显著性水平达到5%。同时，劳动力成本上升削弱了中国劳动密集型制造业的竞争优势，国际市场原材料和能源价格的持续走高加重了制造业企业的负担，产能过剩和环境污染问题制约着中国制造业规模的进一步扩张。处于全球价值链低端的产品附加值不高，产品同质化竞争激烈，这导致我国制造业贸易环境恶化[11] 。园区产业结构趋同、内生动力不足等也将导致高新技术产业园区在关键技术及特定价值链环节上产生路径依赖，锁定在全球产业结构的偏低端[12]。

第三，创汇总额的估计结果也基本符合理论假设，显著性水平至少达到5%，但其对创新效率的直接影响相对较小。

第四，上缴税额的系数显著为负，说明上缴税额对创新效率产生抑制作用，这与一般理论预期相一致。但从具体数值来说，上缴税额实际影响程度则比较小。

（二）面板内生前沿模型估计结果

表1与表2的面板内生前沿模型表明：

第一，内生性检验表明模型设置存在内生性问题。ETA值即文中第四部分实证模型中式（4）所示的η值。表1中η Endogeneity Test 表明卡方值X2=17.28，p=0.005，通过1%的显著性水平，表明模型设置存在内生性问题。η值的详细说明请参见Karakaplan 和 Kutlu （2017a）[8]。

第二，市场结构对非效率项产生显著的负面影响，在控制内生性后，影响程度（绝对值）变小了，其数值从-0.474提高到-0.470。依据表2可知，所有变量通过10%的统计显著性。研发费用与高级研发人员在内生变量科技经费的预测方程中，以及从业人员预测方程中Z值都大于3.16，证明工具有效。

第三，面板内生随机模型的回归系数符号基本保持一致，且市场结构、科技经费和从业人员等重要变量的回归系数显著增强。同时，高级研发对创新效率的影响是正的。因此，高新技术产业园区效率主要决定因素应该是重要技术人员，而且两种模型回归系数的标准差也都比较小，说明回归系数估计比较可靠。

（三）面板内生前沿模型和面板外生前沿模型创新效率的比较

研究发现创新活动从业人员和科技经费对创新活动的影响在面板内生随机前沿模型比面板外生随机前沿模型要大。

通过模型EX的系数估计结果预测高新技术产业园区平均科技经费增加10%，创新效率将增加3.002%。通过模型EN的系数估计发现，当平均科技经费增加10%时，创新效率增加9.079%。模型EX和模型EN预测的创新效率差异约为2068447元（约3倍）。类似地，创新活动从业人员对创新效率的影响在面板内生随机前沿模型比面板外生随机前沿模型要大。通过模型EX的系数估计预测高新技术产业园区平均从业人员增加10%时，创新效率将减少2.028%。面板外生前沿模型和面板内生前沿模型预测的创新效率差异约为2068447元（约4倍）。

通过创新效率的直方图发现，模型EN中创新效率略高于模型EX中所报告的创新效率①。在市场高度集中的地区，这种平均差异更大。说明尽管市场结构对创新效率有正面影响，但在外生性假设下，这种影响被低估了。由于市场集中可能会促进创新效率，因此，外生性假设会导致创新效率向下偏移。另外，分布同质性的Kolmogorov-Smirnov检验表明，這两个模型的创新效率分布在1%的水平上显著不同（p=0.000），并且面板内生随机前沿模型EN的创新效率显著高于模型EX中的该结果。

五、稳健性分析

（一）工具变量充分性

在表3的第二列中，使用了大专以上研发人员数量和年末资产作为处理模型内生性的两个工具变量。在表3的第三列中，采用研发人员全时当量和年末负债作为处理模型内生性的两个工具变量。实证结果与表2和表1的结果非常相似，特别是内生变量的系数和显著性以及内生性检验的结果。而且从预测方程来看，排除工具变量外的其他变量都具有统计意义，其Z值满足了前面提到的经验法则，这证明工具变量是合适的。

（二）空间外溢互动和创新效率的变化

前文指出创新活动的空间互动效应是相当大的，这也是创新效率内生性的重要来源。忽略空间互动会导致参数估计的偏差和政策建议的误导。

为了研究相互作用和溢出效应，参考Millimet和Collier（2008）的研究方法[13]，分析结果显示：表4中的第二列给出了表1中模型EN的扩展版本，其中一组完整的相邻值作为高新技术产业园区低效率的决定因素。表4的第三列进一步扩展了模型，在创新效率边界项中加入了可能忽略的变量，例如高新技术产业园区GDP、金融贷款额[14]。本文发现大多数溢出变量并不是显著有效，只有少数的邻近值在5%水平上显著。将溢出变量作为内生变量进行评估并不会产生不同的估计结果。因此，表4中的结果将提出关于溢出效应重要性的问题。然而，表4中的创新效率低于表1的基准模型EN，这指出了它们对包含相邻值和其他附加变量的敏感性。扩展基准模型大大提高了对数似然值，似然比检验将表明扩展模型EN2比扩展模型EN1或表1中的模型EN拟合的更优。科技经费和从业人员是内生的，它们的效应与表1中的模型EN亦显著为正，并且其效应大小没有实质性差异。

本文使用新技术专利收入作为创新效率的替代变量。当处理模型内生性时，市场结构、科技经费和从业人员均显著为正，影响增加了4倍以上，这与表1和表2中的结果相类似。其余的估计结果与表1的基准估计结果基本相同。

通过比较面板外生随机前沿模型与面板内生随机前沿模型中创新效率的直方图发现两者存在明显差异。研究发现，模型EN中创新效率略高于模型EX中所报告的创新效率，再者，分布同质性的Kolmogorov-Smirnov检验表明，这两个模型的创新效率分布在0.01%的水平上显著不同（p=0.000），并且面板内生随机前沿模型EN的创新效率显著高于模型EX②。

表3、表4和表5的结果表明，表1基本结果是稳健的。也就是说，创新活动中市场结构、科技经费和从业人员对创新效率的有显著的正面影响，如果适当地处理其内生性问题，这些正面影响则会大得多。

六、结论与启示

基于非平衡面板内生随机前沿模型，通过2009-2019年54个高新技术产业园区的非平衡面板数据，研究发现：第一，高新技术产业园区创新效率除外生变量解释外，还应该强调说明创新活动之间的关联、研发费用和市场结构等内生因素的影响。第二，在弥补创新活动内生性的模型中，科技经费和从业人员对创新效率估计影响比较大;如果考虑模型的内生性，市场经济对创新的非效率影响比较大。第三，控制内生性后，创新效率值更高，且创新水平差异的不同导致效率差异更为明显。

基于以上结论，提出如下建议：第一，继续吸引更多高投入研发企业进入高新区。实证研究结果表明，市场结构等变量与高新产业园区效率存在双向反馈机制，如果某个行业所在的某高新产业园区发展比较好，类似的企业也会选择进入。一方面，更多的企业入驻会改变这个行业的竞争态势;另一方面，则又会促进他们的共同创新和创新外溢。因此，高新区应该吸引更多高研发投入的企业进入。第二，加大对高级研发人员的引入。研发人员与高新区效率的负关系说明很多研发人员可能人浮于事，如果只是简单的人数增加，并没有真正从事有价值的创新活动，并没有必然导致高新产业园区效率的提高，因此，需要加大对高级研发人员的引入。第三，增加研发投入，促进产业升级。高新产业园区效率提升很大程度上取决于基础核心技术，只有拥有基础核心技术才能不被别国“卡脖子”，才能真正实现高新产业园区的可持续发展。

注释：

① 限于篇幅，未列出完整的内生面板随机前沿模型与外生面板随机前沿模型频率分布， 可向作者索取相关完整结果。

② 限于篇幅，未列出完整的面板外生随机前沿模型与面板内生随机前沿模型中创新效率的直方图，可向作者索取相关完整结果。

参考文献：

[1] Shee A， Stefanou S E. Endogeneity corrected stochastic production frontier and technical efficiency[J].American Journal of Agricultural Economics， 2015（97）：939-952.

[2] Tran K C， Tsionas E G. Endogeneity in stochastic frontier models：Copula approach without external instruments[J].Economics Letters， 2015（133）：85-88.

[3] Karakaplan， Mustafa U， Levent Kutlu. Endogeneity in panel stochastic frontier models：An application to the Japanese cotton spinning industry[J]. Applied Economics， 2017， 49（59）：5935-5939.

[4] Mutter R L， Greene W H， Spector W， et al. Investigating the impact of endogeneity on inefficiency estimates in the application of stochastic frontier analysis to nursing homes[J].Journal of Productivity Analysis，2013， 39（2）：101-110.

[5] 欧光军，杨青，雷霖.国家高新区产业集群创新生态能力评价研究[J].科研管理，2018，39（8）：63-71.

[6] 余东华，王必好.技术创新效率的内生性与随机变动效应研究：要素投入中知识资本与人力资本的差异化影响[J].南方经济， 2020（1）：76-94.

[7] 陈军，成金华.内生创新、人文发展与中国的能源效率[J].中国人口·资源与环境，2010，20（4）：57-62.

[8] Karakaplan M U， Kutlu L. Handling endogeneity in stochastic frontier analysis[J].Economics Bulletin，2017a（37）：889-891.

[9] Karakaplan， Mustafa U， and Levent Kutlu. School district consolidation policies：endogenous cost inefficiency and saving reversals[J].Empirical Economics， 2019，56（5）：1729-1768.

[10]武增海，李濤.高新技术开发区综合绩效空间分布研究：基于自然断点法的分析[J].统计与信息论坛，2013（3）：82-88.

[11]黄春玲，余颖，黄卓.国家高新区创新效率的实证研究[J].科学学与科学技术管理，2005（2）：100-104.

[12]姜彩楼， 曹杰， 刘维树. 中国高新产业园区效率变动及影响因素研究：基于面板数据的随机前沿分析 [J].经济体制改革，2014（6）：52-56.

[13]Millimet D L， Collier T .Efficiency in public schools：Does competition matter？ [J]. Journal of Econometrics， 2008， 145（1-2）：134-157.

[14]叶海景.政府R&D资助对企业创新效率的影响——基于温州规上工业企业面板数据的随机前沿分析[J].中共浙江省委党校学报，2017，33（6）：116-122.

（责任编辑：钟 瑶）