订单拆分、知情交易概率与风险定价
2021-04-25徐光鲁马超群刘江龙米先华
徐光鲁 马超群 刘江龙 米先华


基金项目:国家社会科学基金项目(19AZD014)、国家自然科学基金项目(71850012)
作者简介:徐光鲁(1990—),男,山东聊城人,博士,中国农业银行博士后科研工作站博士后,研究方向:市场微观结构;马超群(1964—),男,湖南岳阳人,博士,湖南大学工商管理学院教授,博士生导师,研究方向:金融创新与风险管理。
摘 要:基于2018-2020年沪深300指数成分股的高频数据,构建累计拆分订单比变量度量市场订单拆分行为,考虑订单拆分行为对知情交易概率及其风险定价能力的影响。实证发现:订单拆分行为增加了不同算法下知情交易概率的差异,这一差异对流动性和订单规模因素具有稳健性。进一步研究发现:不同的订单拆分水平下,知情交易概率与风险定价之间呈现非线性关系,高订单拆分水平降低了知情交易概率的风险定价能力。
关键词:订单拆分;知情交易概率;风险定价
中图分类号:F830.91 文献标识码:A 文章编号:1003-7217(2021)06-0067-08
一、引 言
知情交易概率作为度量市场信息不对称的主要指标,是金融市场微观结构研究的热点。然而,关于知情交易概率指标与风险定价的研究,目前还没有统一定论。Easley等(1996)[1]首先基于理性预期理论提出知情交易者利用其信息优势,以非知情交易者的损失为代价获得超额收益,从而知情交易概率指标对资产收益产生正向定价效应。而后续学者的实证研究却发现知情交易概率指标的定价效果并不显著[2]甚至产生负向效应[3]。对于这一矛盾性结论并无法从知情交易概率指标估计的样本选取和参数选择的角度进行解释[4]。事实上,知情交易者基于信息不对称进行获利,需要以隐藏其信息优势为前提。特别地,知情交易者通过主动拆分订单方式隐藏其交易主动性,对于基于订单买卖主动性不平衡为度量基础的VPIN指标估计[5]及其市场表现[6,7]产生重要影响。
国内外学者围绕VPIN指标主要研究订单买卖方向划分[8]对VPIN估计的影响,以及不同算法下VPIN指標在事件预警[9,10]、波动率预测[11]、流动性预测[12]、风险定价[13]等方面的表现。但是即使基于同样参数设置和样本数据,VPIN市场表现也存在一定差异。以往文献忽略了VPIN值差异背后的拆分订单行为,而这一行为又可能造成VPIN指标的市场表现具有截然相反的效应。特别是,知情交易概率的本质是订单买卖不平衡性的度量,而订单拆分行为显著影响了买卖订单的不平衡性,这是以往文献忽略的因素。另外,虽然部分研究认为订单拆分对知情交易概率产生重要影响[5,14],但是鲜有文献直接检验拆分订单行为对知情交易概率的影响机制。这主要是因为基于交易价格变化度量的市场拆分订单指标受主观划分交易规模因素影响,其研究结论缺少稳健性。同时,上述指标只能间接验证市场拆分订单行为的存在性,难以量化拆分订单行为及其影响。
本文重点研究拆分订单行为对知情交易概率指标的影响,并力图弥补以往研究不足。首先,研究表明知情交易概率指标对估计算法的选取具有一定的敏感性,这一敏感性源于市场投资者拆分订单行为。实证结果表明,订单拆分行为增加了两种算法下VPIN值差异,这一边际效应对流动性和规模因素具有稳健性。其次,验证了我国股票市场存在的拆分订单行为,并在Pppe等(2016)[5]研究基础上提出了累计拆分订单比指标以度量拆分订单交易行为。该指标有助于克服间接指标受主观划分交易规模的不利影响。最后,本文研究有助于解释知情交易概率指标对风险定价产生或正或负的矛盾性结论。研究表明,在高订单拆分水平下VPIN指标具有显著负向风险定价能力;反之,VPIN对风险定价产生正向影响。
二、算法回顾与研究假设
(一)知情交易概率估计:真实值算法(RVA算法)VS启发式算法(BVC算法)
Easley等(1996[1],1997[15,16])提出度量知情交易概率的PIN指标,Easley等(2012[14],2011[17],2012[18])进一步拓展PIN指标并将其发展成适用于高频环境的VPIN指标。根据Easley等(2012[14],2011[17],2012[18])的研究,VPIN的计算公式为
其中,n为总交易篮子数,V表示每个等交易量篮子τ包含的交易量,VBτ、VSτ分别是每个等交易量篮子τ中买、卖交易量,即V=VBτ+VSτ。
对于每个交易篮子中买卖交易量的划分,通常采用真实值算法(RVA算法)和启发式算法(BVC算法)两种算法。下文中提及的两种VPIN值指两种算法下计算的VPIN值。两种算法的区别在于,前者根据逐笔交易数据记录的买、卖标识计算每个交易篮子中买卖订单不平衡,后者根据每个交易篮子内交易价格变化,近似划分买卖订单不平衡。其中在BVC算法划分买卖交易过程中,通常选取1 min作为每个等交易量篮子中的交易间隔,根据交易间隔价格变化ΔPi和价格变化标准差σΔP,划分该交易篮子τ中的买卖交易量,即式(1)中VBτ、VSτ不再基于逐笔交易数据买卖字段划分,而是根据交易篮子价格变化近似划分,其划分过程如下:
其中,V为每一分钟对应的交易量,t(τ)为每个等交易量篮子τ中包含的时间间隔数,Z为累计分布函数。
(二)研究假设
市场参与者学习到知情交易者传递的信息时,知情交易者并不能获得超额收益[19]。因此,拆分订单行为是市场投资者隐藏交易信息的一种交易策略。不同学者以订单流不平衡存在的相关性,验证了不同市场存在的拆分订单行为[20-22]。但拆分订单行为对两种算法下VPIN指标的影响并不相同。交易者进行订单拆分意味着交易量固定的情况下,交易笔数增加。这一订单拆分行为增加的交易笔数,影响了市场流动性,改变了市场潜在的买卖订单不平衡性,影响了基于真实值算法下度量的VPIN(RVA)。例如,Duarte和Young(2009)[3]基于公共事件引发的流动性冲击与知情交易之间存在的相关性,实证发现VPIN(RVA)指标度量的风险因素可能包含流动性风险因素,从而VPIN(RVA)指标容易受到市场流动性冲击的影响。李平等(2020)[23]发现在不同的流动性水平下VPIN(RVA)表现并不相同。因此,拆分订单行为影响了VPIN(RVA)估计水平。而基于交易价格近似划分买卖订单不平衡的VPIN(BVC)指标,避免了拆分订单这一行为的影响。Pppe等(2016)[5]实证发现交易笔数变量对两种算法下VPIN值的差异具有显著解释效应。因此,本文提出如下研究假设:
H1 市场存在的订单拆分行为增加了两种算法下VPIN值的差异。
已有文献分别以美国[13]、中国[23]、中国台湾[24]证券市场为研究对象,发现知情交易概率指标的风险定价能力并不相同。尽管部分文献从流动性因素[3]和日历效应[25]等角度对VPIN(RVA)风险定价差异进行了解释,但由于上述文献在研究对象和参数设置方面存在不一致,其研究结论缺乏可比性,更难以挖掘不同算法下VPIN市场表现差异背后的原因。特别是,知情交易者通过拆分订单以隐藏其交易主动性,并进一步伪装成流动性提供者,显著降低了非知情交易者要求的风险溢价补偿[7]。这一隐藏交易行为,一方面,挑战了理性预期理论中非知情交易者要求更高的风险溢价以弥补知情交易者带来的逆向选择风险结论;另一方面,使知情交易者提交的订单仅停留在交易簿一侧,将其置于交易被动方以等待非知情交易者主动发起交易,降低指令流“毒性”,從而降低了交易价格中非知情交易者所要求的流动性风险溢价,进一步影响了基于真实值算法下度量的VPIN(RVA)指标的风险定价能力。对于启发式算法下的VPIN(BVC)指标,其风险定价能力受拆分订单行为的影响较小。陈国进等(2019)[26]发现VPIN(BVC)显著影响横截面和时序风险溢价,并且在控制了其他市场因素后,VPIN(BVC)定价效果依然显著。基于此,从风险溢价的角度提出如下研究假设:
H2 市场拆分订单水平越高,两种算法下VPIN指标的风险定价能力差别越大。
三、研究设计
(一)样本选择与数据来源
本文研究样本为沪深300指数成分股267只股票(剔除日交易数据不完整的样本33个)2018年1月到2020年2月共531天的数据,合计样本量为141777。使用的日内高频交易数据即逐笔交易数据来自国泰安Level-2高频数据库,其他数据来自万得(Wind)数据库。高频数据的批量处理和计算,使用Matlab2012b软件,实证研究使用Stata13.0软件。
(二)变量定义
1.被解释变量(VPIN_delta)和股票收益率(Return)。
因变量VPIN_delta为VPIN(RVA)值和VPIN(BVC)值之差。在参数选择方面,两种算法均采用相同参数设置以确保可比性,见图1。每个等交易量篮子的交易量V为月均交易量的五十分之一,每个VPIN包含的交易篮子数n为50,交易间隔为1 min。股票收益率Return为月度收益率。
2.累计拆分订单比(OrderSlice)。图2给出了日内5 min时间段平均订单流不平衡统计柱状图。可以看出,订单流不平衡序列呈现聚集性,这与王春峰等(2007)[21]、Shenoy和Zhang(2007)[22]研究中发现的我国股票市场存在订单拆分行为的研究结论相一致。由于日内订单拆分行为也可以来自市场存在的羊群效应和其他流动性投资者的“试水”行为。前者模仿他人拆分订单的行为,并伪装成真正私有信息的拥有者,延缓了买压、卖压的释放,其行为效果可视同隐藏信息的交易者;后者考虑到市场交易成本的存在可以忽略①。为了避免上述因素带来的研究偏误,下文考虑了流动性分组和规模分组对拆分订单的影响。
参考Pppe等(2016)[5]的研究,本文基于逐笔交易数据中主动买、卖标识字段和委托买、卖ID字段统计拆分订单次数,采用累计拆分订单比形式度量市场隐藏交易者拆分订单行为。累计拆分订单比变量表达式为:
其中,n为逐笔交易数据中主动买卖标识为连续重复的买或卖方标识的区间个数,nj为某个区间内连续重复的委买ID或委卖ID次数之和,nk为总交易次数。具体讲,首先,统计每个VPIN内逐笔交易数据中主动买卖标识为连续重复的买或卖方标识的区间个数n。其次,对于区间标志为主动买方标志的区间j,统计该区间内连续重复的委卖ID次数,记为主动拆分订单次数;反之,统计该区间内连续重复的委买ID次数,记为主动拆分订单次数。最后,累计所有连续区间内委买和委卖ID次数,记为主动拆分订单次数,并与总交易次数相除,得到每个VPIN下累计拆分订单比。
3.时间区间(TimeBars)。
参考Andersen和Bondarenko(2014)[4]的研究,时间区间变量为每个VPIN值包含的交易间隔数。
4.交易量波动率(VolumeVola)和收益波动率(ReturnVola)。由于交易量和价格并不能直接作为解释变量,参考Pppe等(2016)[5]的研究,选取交易量波动率和收益波动率作为反映特定交易模式的变量。
5.行情指标(MarketRet)。
行情指标(MarketRet)反映了每个VPIN值所对应的交易区间内的收益情况,0代表正收益,-1代表负收益。
6.其他控制变量。参考李平等(2020)[23]的研究,选取换手率、市值规模、贝塔系数和账面市值比作为控制变量,其中上述变量采用面板数据形式。
(三)模型设计与研究方法
本文构建计量模型进一步分析以上解释变量对VPIN值差异的边际效应,模型1的基本表达式为:
四、实证分析与结果
表1表明两种算法下知情交易概率之差VPIN_delta的均值为0.115,通过显著性检验发现,VPIN_delta均值不显著为0,说明两种算法下知情交易概率值存在不同。累计拆分订单比最高值与最低值相差0.55,说明不同股票之间市场投资者拆分订单行为存在一定差异,这为从拆分订单行为角度解释不同知情交易概率指标及其定价效果之间的差异提供了充分依据。本文采用常用的面板单位根检验方法LLC和IPS方法进行检验,以避免伪回归问题。表2给出了检验结果。由表2可知,在两种单位根检验下,均强烈拒绝“面板数据存在单位根”的原假设,即认为该面板数据是平稳的,可以用于面板数据分析。
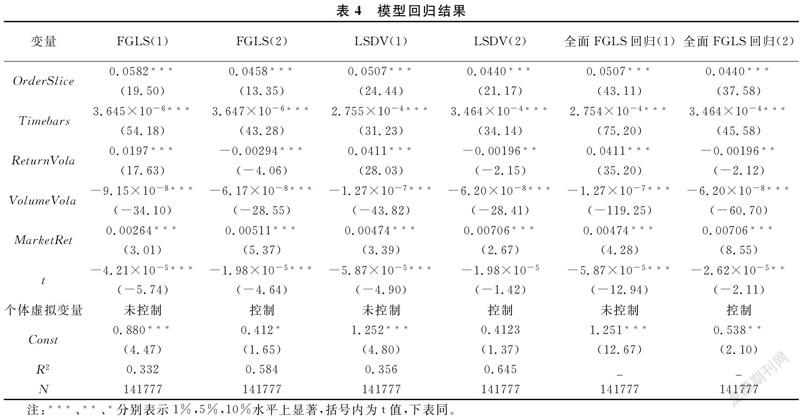
考虑到长面板数据可能存在组间异方差、组内自相关、组间截面相关等问题,采用Greene及Wooldridge提供的沃尔德检验,进行组间异方差和组间自相关检验,而组间截面相关问题,则采用Pesaran、Friedman提出的半参数检验以及 Frees提供的参数检验方法。表3给出了模型1的最终检验结果,其中组间方差沃尔德检验的结果为2041.92,在1%显著性水平下强烈拒绝组间同方差的原假设,表明存在组间异方差;组内自相关沃尔德检验的结果为317.083,强烈拒绝不存在一阶组内自相关的原假设,表明样本数据内存在组内自相关性;而组间自相关检验,至少两种检验方法在1%显著性水平下拒绝无组间同期相关的原假设,可以认为存在组间自相关问题。因此,本文选择全面FGLS方法对模型1进行估计。表4给出了模型1的估计结果,各自变量对被解释变量均具有较强的解释效应。进一步通过比較FGLS、LSDV、全面FGLS回归结果,总体估计结果并未出现显著差异,说明各解释变量与被解释变量之间的关系相当稳健。各模型在加入个体虚拟变量前后,其解释变量的估计系数未发生显著变化,但是收益波动率变量ReturnVola的系数出现了反转。已有研究表明交易量[27]和收益波动率变量[28]在其他交易因素的影响下具有较强的个体效应。换言之,本文模型可能存在较强的个体固定效应。从交易量波动率变量和收益率波动率变量在加入虚拟变量前后的表现看,交易量波动率变量在加入个体虚拟变量前后,其系数和显著性均未发生显著改变,而收益率波动率变量在加入虚拟变量前后,系数发生了反转。这主要由于估计VPIN所采用的固定交易量尺度抵消了交易量变量的个体效应,因此其回归系数并不受个体效应的影响;而收益率波动率受到个体效应影响,在加入虚拟变量前后,其系数发生显著变化,这也证实了收益波动率所具有的个体效应。基于此,本文在模型中加入虚拟变量控制各股票的个体效应以防止遗漏变量。总体看,全面FGLS回归结果比仅考虑组内自相关的FGLS方法和仅考虑组间异方差、组间同期相关的面板校正标准误方法LSDV的估计结果更为可靠。下文分析主要以全面FGLS回归结果为主。从表4估计结果可以看出,累计拆分订单比变量OrderSlice的系数显著为正,这一结果符合前文研究假设部分中的分析[5];同时,从流动性角度来看,其主动隐藏自身交易的行为,降低了市场价格信息含量,更容易引发市场羊群效应,进一步加剧市场买卖订单不平衡性,从而使得VPIN(RVA)高估的误差偏大,增加了两种VPIN值差异,这一结果验证了假设1,说明隐藏交易者拆分订单行为增加了两种算法下VPIN值的差异。
通过表4进一步分析发现,时间区间变量Timebars的系数为正且显著,说明交易强度越强,两种VPIN值差别越大。Chung等(2016)[29]代表性的研究认为交易强度的增加源于噪声交易。交易噪声对即时价格的冲击具有更强的效应[30],同时这一噪声具有明显的个体效应[31]。而模型1在控制了个体效应后,时间区间变量的系数仍然显著为正,说明时间区间变量对VPIN值差异解释显著的背后,并非噪声冲击所带来的交易强度变化造成的,而是源于信息驱动交易者“有意而为之”的交易行为,即在交易强度较高进而非知情交易者聚集的情况下,知情交易者得以通过主动拆分订单行为隐藏了其交易主动性,从而交易强度越高,两种算法下VPIN值的差异越大。市场行情指标MarketRet系数为正,说明市场行情上涨的情况下,两种算法下VPIN值的差异较大;而在市场行情下跌的情况下,VPIN值的差异越小。
表5给出分组检验的回归结果,其中流动性分组以交易笔数变量作为分组变量,规模分组以交易量变量作为分组变量。可以看出,各分组下累计拆分订单比变量OrderSlice对VPIN_delta的影响均显著为正,进一步验证了假设1,即拆分订单行为增加了两种算法下度量的VPIN差异,这一差异对流动性和订单规模因素仍然稳健。本文进一步通过Suest检验研究了累计拆分订单比变量OrderSlice的边际效应。在进行分组估计和组间系数检验之前,首先,对面板数据各变量进行去中心化处理,以消除存在的个体效应;其次,进行Suest检验。检验结果表明,Prob>Chi2=0.0027<0.01,拒绝“两组回归系数不存在显著差别”的原假设,可以认为,不同流动性分组下累计拆分订单比变量OrderSlice对两种算法下VPIN差异的边际效应存在显著不同。这主要由于,高流动性市场环境中存在较为明显的羊群效应,投资者之间的相互模仿行为,延缓了买卖压的释放,更加显著地影响了市场潜在的订单不平衡,对两种算法下VPIN差异影响更大,因此,在不同的流动性分组下,拆分订单的边际效应存在显著差异;对于规模分组而言,检验结果表明,Prob>chi2结果大于0.01,无法拒绝“两组回归系数不存在显著差别”的原假设,可以认为,不同规模分组下累计拆分订单比变量OrderSlice对两种算法下VPIN差异的边际效应不存在显著不同。这主要因为,虽然不同订单规模对价格冲击程度不同[32,33],但交易成本的存在使得小规模订单仍不可避免地对价格形成冲击[6],这使得基于价格划分买卖订单不平衡的VPIN(BVC)指标更加稳健。因此,在不同规模订单水平下,拆分订单行为对两种算法下VPIN值差异的边际影响不存在显著不同。综上,不同的流动性分组以及不同规模分组下,拆分订单对两种算法下VPIN值的差异的边际影响不同,但对两种算法下VPIN值差异的影响均显著,进一步验证了假设1。
五、拆分订单对知情交易概率指标与股票收益
的影响
隐藏交易者通过拆分订单的方式是否真正“拆分”了知情交易概率指标度量的信息风险?换言之,拆分订单行为是否影响了两种算法下VPIN指标被定价的能力。本文在以上研究基础上进一步分析了拆分订单行为对知情交易概率与风险定价关系的影响。回归模型2设定为:
为了避免VPIN日内交易模式对收益率的影响,模型2采用月度数据进行回归。同时,对解释变量采用滞后一期处理以避免内生性问题,并进一步在解释变量中加入被解释变量Return的滞后项以防止遗漏变量问题。表6给出了模型2的估计结果,其中表6中(1)代表采用VPIN(RVA)估计的结果,(2)代表采用VPIN(BVC)估计的结果。
表6显示虚拟变量以累计拆分订单比变量为分组依据,1代表高累计拆分订单比,0代表低累计拆分订单比。可以看出,不同的累计拆分订单比水平显著影响了股票收益,并且对知情交易概率指标与股票收益的关系产生影响。具体来讲,在低累计拆分订单比分组中,两种算法下VPIN对股票收益产生正向影响;而在高累计拆分订单比组中,两种算法下VPIN对股票收益的边际效应相反,验证了假设2。其中真实值算法下VPIN(RVA)对股票收益率产生显著的负向效用。本文认为,主要存在以下两点原因:一是隐藏交易者对订单进行拆分,增加了交易笔数,进一步增加了买卖订单不平衡性,从而使得基于真实值算法下计算的VPIN(RVA)值存在高估的可能;二是隐藏交易者通过拆分订单方式使自身处于交易的被动方,隐藏了其交易主动性,造成市场指令流毒性和逆向选择风险降低的表象,蒙蔽了非知情交易者,使得其要求的风险溢价降低,从而VPIN(RVA)与资产收益率生了显著负向效应。这与已有研究中采用真实值算法计算的VPIN(RVA)对资产收益产生负向效应的结论相一致[19]。
六、稳健性检验
模型1的准确估计仍面临内生性问题。根据表3中模型1的沃尔德检验结果,扰动项存在一阶组内自相关性。而采用滞后项作为工具变量的差分GMM方法由于T较长存在较大偏差,因此使用偏差校正LSDV法进行动态面板估计以避免内生性问题。同时,为了避免指标选取对本文结论造成偏误,参考Pppe等(2016)[5]的研究,对模型1采用累计拆分订单次数OrderSlicenum进行变量替换,其中累计拆分订单次数为公式(3)中的∑nj=1∑nji=1IDi,其结论均未改变,限于篇幅,未详细列出。
七、结 论
理性预期理论指出信息不对称带来的逆向选择风险增加了市场投资者要求的风险溢价,从而信息不对称水平越高,资产收益越高。然而基于买卖订单不平衡性为度量基础的知情交易概率指标对资产收益的影响并不一致,甚至产生截然相反的定价效应。针对这一矛盾性结论,以往研究忽略了市场存在的拆分订单行为对知情交易概率指标估计及其市场表现的影响。特别是,知情交易者通过拆分订单的交易方式隐藏了交易的主动性,对基于买卖主动性不平衡为度量基础的VPIN指标产生显著影响。本文考虑订单拆分这一隐藏交易行为,并构建了累计拆分订单比指标度量拆分订单的隐藏交易行为,分析拆分订单对VPIN估计及风险定价的影响。研究发现:(1)拆分订单行为增加了两种算法下VPIN值的差异,通过进一步流动性分组和交易规模分组,发现这一差异对流动性因素和交易规模因素具有稳健性;(2)在风险定价方面,啟发式算法下VPIN(BVC)指标对资产收益具有显著正向解释效应,其风险定价能力更加稳健;而真实值算法下的VPIN(RVA)指标的风险定价能力随不同拆分订单水平不同产生截然相反的定价效果,其中在高拆分订单水平下VPIN(RVA)指标对股票收益率产生显著负向效应。这一研究发现解释了已有研究中知情交易概率指标对股票收益产生或正或负的矛盾性结论。
本文的分析及结论对知情交易概率与风险定价关系的研究具有重要意义。根据研究结论,提出以下建议:(1)知情交易概率指标对不同估计算法的选取具有一定的敏感性,这一敏感性源于市场存在的拆分订单的隐藏交易行为。在知情交易概率指标的相关研究中,需要考虑相关研究结论对拆分订单行为因素的稳健性。(2)启发式算法下度量的知情交易概率指标比真实值算法下的知情交易概率指标更加稳健,能够克服交易模式和交易策略带来的影响,可以作为一种有效的监管手段,应用到市场微观结构等其他领域。
注释:
① 高频交易者基于交易策略的驱动通常会拆分订单以获利,其拆分订单行为动机和行为表现与隐藏信息的知情交易者并不矛盾。通常高频交易者具有一定信息优势,也是知情交易者。另外,对于其他原因导致的日间拆分订单行为不予考虑,主要因为,一是日间拆分订单行为可视同基于不同信息的隐藏交易行为;二是日间订单流不平衡自相关性并不显著[21,22]。
参考文献:
[1] Easley D, Kiefer N M, OHara M, et al. Liquidity, information, and infrequently traded stocks[J]. Journal of Finance, 1996, 51(4):1405-1436.
[2] Agudelo D A, Giraldo S, Villarraga E. Does PIN measure information? Informed trading effects on returns and liquidity in six emerging markets[J]. International Review of Economics & Finance, 2015, 39:149-161.
[3] Duarte J, Young L. Why is PIN priced?[J]. Journal of Financial Economics, 2009, 91(2):119-138.
[4] Andersen T G, Bondarenko O. VPIN and the flash crash[J]. Journal of Financial Markets, 2014, 17:1-46.
[5] Pppe T, Moos S, Schiereck D. The sensitivity of VPIN to the choice of trade classification algorithm[J]. Journal of Banking & Finance, 2016(73):165-181.
[6] Kyle A.S. Continuous auctions and insider trading[J]. Econometrica:Journal of the Econometric Society, 1985,56(6):1315-1335.
[7] Anand A, Chakravarty S. Stealth trading in options markets[J]. Journal of Financial and Quantitative Analysis, 2007,42(1):167-187.
[8] Chakrabarty B, Pascual R, Shkilko A. Evaluating trade classification algorithms:Bulk volume classification versus the tick rule and the Lee-Ready algorithm[J]. Journal of Financial Markets, 2015, (25):52-79.
[9] Easley D, López de Prado M M, OHara M. The microstructure of the “flash crash”:flow toxicity, liquidity crashes, and the probability of informed trading[J]. Journal of Portfolio Management, 2011, 37(2):118-128.
[10]Bugeja M, Patel V, Walter T. The microstructure of Australian takeover announcements[J]. Australian Journal of Management, 2015, 40(1):161-188.
[11]Kang J, Kwon K Y, Kim W. Flow toxicity of high-frequency trading and its impact on price volatility:Evidence from the KOSPI 200 futures market[J]. Journal of Futures Markets, 2020, 40(2):164-191.
[12]Cheung W M, Chou R K, Lei A C. H. Exchange-traded barrier option and VPIN:Evidence from Hong Kong[J]. Journal of Futures Markets, 2015, 35(6):561-581.
[13]Borochin P, Rush S. Identifying and pricing adverse selection risk with VPIN[EB/OL]. (2016-02-01)[2021-09-25].http:∥ssrn.com/abstract=2599871.
[14]Easley D, Lopez de Prado M, OHara M. Bulk classification of trading activity[J]. Johnson School Research Paper Series, 2012, 8(6):14.
[15]Easley D, Kiefer N M, OHara M. One day in the life of a very common stock[J]. Review of Financial Studies, 1997, 10(3):805-835.
[16]Easley D, Kiefer N M, OHara M. The information content of the trading process[J]. Journal of Empirical Finance, 1997, 4(2/3):159-186.
[17]Easley D, López de Prado M M, OHara M. The exchange of flow toxicity[J]. Journal of Trading, 2011, 6(2):8-13.
[18]Easley D, López de Prado M M, OHara M. Flow toxicity and liquidity in a high-frequency world[J]. Review of Financial Studies, 2012, 25(5):1457-1493.
[19]馬超群,徐光鲁,刘伟, 等. 询价制度改革、知情交易者概率与 IPO 溢价[J]. 中国管理科学, 2018, 26(8):1-12.
[20]Chordia T, Roll R, Subrahmanyam A. Evidence on the speed of convergence to market efficiency[J]. Journal of Financial Economics, 2005, 76(2):271-292.
[21]王春峰, 孙永亮, 房振明, 等. 订单流不平衡对股票价格的冲击效应实证研究[J]. 北京理工大学学报(社会科学版), 2007 (2):71-75.
[22]Shenoy C, Zhang Y J. Order imbalance and stock returns:Evidence from China[J]. The Quarterly Review of Economics and Finance, 2007, 47(5):637-650.
[23]李平,汤怀林,王张琦,等. 知情交易概率与风险定价——基于不同 PIN 测度方法的比较研究[J]. 管理科学学报, 2020, 23(1):33-46.
[24]Lee Y H, Liu W C, Hsieh C L. Informed trading of futures markets during the financial crisis:Evidence from the VPIN[J]. International Journal of Economics and Finance, 2017, 9(9):123-132.
[25]Kang M. Probability of information-based trading and the January effect[J]. Journal of Banking & Finance, 2010, 34(12):2985-2994.
[26]陈国进,张润泽,谢沛霖,等. 知情交易, 信息不确定性与股票风险溢价[J]. 管理科学学报, 2019 (4):53-74.
[27]陈浪南,罗嘉雯,刘昊. 基于 TVP-VAR-GCK 模型的量价时变关系研究[J]. 管理科学学报, 2015, 18(9):72-85.
[28]Dutt T, Humphery-Jenner M. Stock return volatility, operating performance and stock returns:International evidence on drivers of the ‘low volatilityanomaly[J]. Journal of Banking & Finance, 2013, 37(3):999-1017.
[29]Chung K H, Ryu D. Trade duration, informed trading, and option moneyness[J]. International Review of Economics & Finance, 2016, 44:395-411.
[30]谢文杰,李牧遥,周炜星. 噪声交易者、交易行为多样性与即时价格冲击[J]. 管理科学学报, 2020, 23(4):98-109.
[31]Cai B M, Cai C X, Keasey K. Which trades move prices in emerging markets?:Evidence from Chinas stock market[J]. Pacific-Basin Finance Journal, 2006, 14(5):453-466.
[32]Chan K, Fong W M. Trade size, order imbalance, and the volatility-volume relation[J]. Journal of Financial Economics, 2000, 57(2):247-273.
[33]Alexander G J, Peterson M A. An analysis of trade-size clustering and its relation to stealth trading[J]. Journal of Financial Economics, 2007, 84(2):435-471.
(責任编辑:厉 亚)
