Fundamentals of quasigroup Hopf group-coalgebras
2021-04-24ZhangSenlinWangShuanhong
Zhang Senlin Wang Shuanhong
(School of Mathematics, Southeast University, Nanjing 211189, China)
Abstract:A large class of algebras (possibly nonassociative) with group-coalgebraic structures, called quasigroup Hopf group-coalgebras, is introduced and studied. Quasigroup Hopf group-coalgebras provide a unifying framework for the classical Hopf algebras and Hopf group-coalgebras as well as Hopf quasigroups. Then, basic results similar to those in Hopf algebras H are proved, such as anti-(co)multiplicativity of the antipode S:H→H, and S2=id if H is commutative or cocommutative.
Key words:Hopf quasigroup; group-coalgebra; quasigroup Hopf group-coalgebra; convolution algebra
In 2000, Turaev[1]introduced, for groupπ, the notion of a modular crossedπ-category and showed that such a category gives rise to a three-dimensional homotopy quantum field theory with target spaceK(π,1). Examples ofπ-categories can be constructed from the so-called Hopfπ-coalgebras also introduced in Ref.[1]. The notion of a Hopfπ-coalgebra generalizes that of a Hopf algebra. Some mathematicians have contributed to the subject[1-7]. The subject of Hopfπ-coalgebras continues to grow in some directions. More recent considerations have led to generalizations of the notion of Hopfπ-coalgebras.
The authors in Refs.[8-10] proved that, for every Malcev algebraL, there is an algebraU(L) and a monomorphismι:L→U(L) ofLinto the commutator algebraU(L) such that the image ofLlies into the alternative center ofU(L), andU(L) is a universal object with respect to such homomorphisms.
The algebraU(L), in general, is not alternative, but it has a basis of Poincaré-Birkhoff-Witt type overLand inherits some good properties of universal enveloping algebras of Lie algebras. IfGis a smooth Moufang loop with Malcev algebra (L,[,]) not of characteristic 2, 3, as tangent spaces ofG, then the authors in Ref.[11] showed that the enveloping algebraU(L) is a Moufang Hopf quasigroup with the structure mapsΔ:U(L)→U(L)⊗U(L),ε:U(L)→kdefined byΔ(x)→x⊗1+1⊗xandε(x)=0 for allx∈Lextended toU(L) as algebra homomorphisms, andS:U(L)→U(L) defined byS(x)=-xextended as an antialgebra homomorphism. LetGact onU(L) by Hopf quasigroup endomorphisms induced by the quasigroup conjugation. LetU(L)G={U(L)α}α∈G, where the algebraU(L)αis a copy ofU(L) for eachα∈G. Fix an identification isomorphism of algebrasiα:U(L)→U(L).
For anyα,β∈G, one defines a comultiplicationΔα,β:U(L)αβ→U(L)α⊗U(L)βbyΔα,β(iαβ(h))=∑iα(h1)⊗iα(h2) for anyh∈U(L). The counitε:U(L)1→kis defined byε(i1(h))=ε(h) forh∈U(L). For anyα∈G, the antipodeSα:U(L)α→U(L)α-1is given bySα(iα(h))=iα-1(S(h)). The constructions above give a so-called quasigroup Hopf G-coalgebra in this paper.
The aim of the present paper is to establish the existence of integrals for a quasigroup Hopfπ-coalgebras.
Throughout the paper, we letπbe a discrete group (with neutral element 1) andkbe a field (although much of what we do is valid over any commutative ring). We use the Sweedler notation to express the coproduct of a coalgebraCasΔ(c)=∑c1⊗c2[12]. We setk*=k{0}. All algebras are supposed to be overkand unitary, but not necessarily associative. The tensor product ⊗=⊗kis always assumed to be overk. IfUandVarek-spaces,σU,V:U⊗V→V⊗Uwill denote the flip map defined byσU,V(u⊗v)=v⊗u.
1 Preliminaries
1.1 Group-coalgebras
We recall from Ref.[2] that aπ-coalgebra (overk) is a familyC={Cα}α∈πofk-spaces endowed with a familyΔ={Δα,β:Cαβ→Cα⊗Cβ}α,β∈πofk-linear maps (the comultiplication) and ak-linear mapε:C1→k(the counit) such thatΔis coassociative in the following sense that, for anyα,β,γ∈π,
The coassociativity axiom
(Δα,β⊗idCγ)Δαβ,γ=(idCα⊗Δβ,γ)Δα,βγ
The counit axiom
(idCα⊗ε)Δα,1=idCα=(ε⊗idCα)Δ1,α
Note that (C1,Δ1,1,ε) is the usual coalgebra.
We extend the Sweedler notation for a comultiplication in the following way: for anyα,β∈πandc∈Cαβ, we write
Δα,β(c)=∑c(1,α)⊗c(2,β)∈Cα⊗Cβ
or shortly, if we leave the summation implicit,Δα,β(c)=c(1,α)⊗c(2,β). The coassociativity axiom gives that, for anyα,β,γ∈π, andc∈Cαβγ,
c(1,αβ)(1,α)⊗c(1,αβ)(2,β)⊗c(2,γ)=c(1,α)⊗c(2,βγ)(1,β)⊗c(2,βγ)(2,γ)
The element ofCα⊗Cβ⊗Cγis written asc(1,α)⊗c(2,β)⊗c(3,γ). By iterating the procedure, we define inductivelyc(1,α1)⊗…⊗c(n,αn), for anyc∈Cα1…αn.
1.2 Convolution algebras
LetC=({Cα},Δ,ε)α∈πbe aπ-coalgebra and (A,m,1A) be an (not necessarily associative) algebra with multiplicationmand unit element 1A. For anyf∈Homk(Cα,A) andg∈Homk(Cβ,A), we define their convolution product by
f*g=m(f⊗g)Δα,β∈Homk(Cαβ,A)
Using the coassociativity axiom and counit axiom, one verifies that thek-space
endowed with the convolution product * and the unit elementε1A, is a not necessarily associativeπ-graded algebra, called convolution algebra.
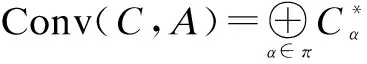
1.3 Hopf quasigroups
Recall from Definition 4.1 in Ref.[11] that a Hopf quasigroup is a unital algebraH(possibly nonassociative) equipped with algebra homomorphismsΔ:H→H⊗H,ε:H→kforming a coassociative coalgebra and a mapS:H→Hsuch that
m(S⊗m)(Δ⊗id)=m(id⊗m)(id⊗S⊗id)(Δ⊗id)=ε⊗id
m(m⊗id)(id⊗S⊗id)(id⊗Δ)=m(m⊗S)(id⊗Δ)=id⊗ε
Remark 1A Hopf quasigroup is a Hopf algebra iff its product is associative.
2 Quasigroup Hopf Group-Coalgebras
Definition 1AquasigroupHopfgroup-coalgebraoverπisaπ-coalgebraH=({Hα}α∈π,Δ={Δα,β:Hαβ→Hα⊗Hβ}α,β∈π,ε),endowedwithafamilyS={Sα:Hα→Hα-1}α∈πofk-linearmaps(theantipode)suchthatthefollowingconditionshold:
Axiom 1Each (Hα,mα,1α) is not a necessarily associative algebra with multiplicationmαand unit element 1α∈Hα.
Axiom 2For allα,β∈π,Δα,βandεare algebra homomorphisms .
Axiom 3For allα∈π,
mα(idHα⊗mα)(Sα-1⊗idHα⊗idHα)(Δα-1,α⊗idHα)=
ε⊗idHα=mα(idHα⊗mα)(idHα⊗Sα-1⊗idHα)(Δα,α-1⊗idHα)
Axiom 4For allα∈π,
mα(mα⊗idHα)(idHα⊗Sα-1⊗idHα)(idHα⊗Δα-1,α)=
idHα⊗ε=mα(mα⊗idHα)(idHα⊗idHα⊗Sα-1)(idHα⊗Δα,α-1)
In this paper, a quasigroup Hopf group-coalgebra overπis called a quasigroup Hopfπ-coalgebra. We note that the notion of a quasigroup Hopfπ-coalgebra is not self-dual and that (H1,m1,11,Δ1,1,ε,S1) is a (classical) Hopf quasigroup. One can easily verify that a quasigroup Hopfπ-coalgebra is a Hopfπ-coalgebra if and only if its product is associative.
Definition 21) A quasigroup Hopfπ-coalgebraHis commutative if eachmαis commutative.
2) A quasigroup Hopfπ-coalgebraH=({Hα},Δ,ε)α∈πis cocommutative if, for anyα∈π,Δα,α-1=σHα-1,HαΔα-1,α, i.e. for anyh∈H1,h(1,α)⊗h(2,α-1)=h(2,α)⊗h(1,α-1).
3) A quasigroup Hopfπ-coalgebraH=({Hα},Δ,ε)α∈πis the first flexible if
Sα-1(h(1,α-1))(gh(2,α))=(Sα-1(h(1,α-1))g)h(2,α)
∀α∈π,h∈H1,g∈Hα
and the second flexible if
h(1,α)(gSα-1(h(2,α-1)))=(h(1,α)g)Sα-1(h(2,α-1))
∀α∈π,h∈H1,g∈Hα.
4) A quasigroup Hopfπ-coalgebraH=({Hα},Δ,ε)α∈πis the first alternative if, for anyα∈π,h∈H1,g∈Hα,
Sα-1(h(1,α-1))(h(2,α)g)=(Sα-1(h(1,α-1))h(2,α))g
g(Sα-1(h(1,α-1))h(2,α))=(gSα-1(h(1,α-1)))h(2,α)
and the second alternative if, for anyα∈π,h∈H1,g∈Hα,
h(1.α)(Sα-1(h(2,α-1))g)=(h(1,α)Sα-1(h(2,α-1)))g
g(h(1,α)Sα-1(h(2,α-1)))=(gh(1,α))Sα-1(h(2,α-1))
5) A quasigroup Hopfπ-coalgebraH=({Hα},Δ,ε)α∈πis called the first Moufang if, for anyα∈π,h∈H1,g,f∈Hα,
Sα-1(h(1,α-1))(g(h(2,α)f))=((Sα-1(h(1,α-1))g)h(2,α))f
and the second Moufang if, for anyα∈π,h∈H1,g,f∈Hα,
h(1,α)(g(Sα-1(h(2,α-1))f))=((h(1,α)g)Sα-1(h(2,α-1)))f

The antipodeS={Sα}α∈πofHis said to be bijective if eachSαis bijective. We will later show that it is bijective wheneverHis of finite type[12].
Example 1Let (H,m,Δ,ε,S) be a Hopf quasigroup and the groupπact onHby Hopf quasigroup endomorphisms.
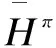
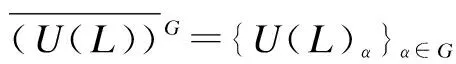
Theorem 1LetHbe a quasigroup Hopfπ-coalgebra. Then
①mα(Sα-1⊗idHα)Δα-1,α=1αε=mα(idHα⊗Sα-1)Δα,α-1, ∀α∈π.
②Sα(ab)=Sα(b)Sα(a),∀α∈π,a,b∈Hα.
③Sα(1α)=1α-1,∀α∈π.
④Δβ-1,α-1Sαβ=σHα-1,Hβ-1(Sα⊗Sβ)Δα,β,∀α,β∈π.
⑤εS1=ε.
Proof① is obtained by applying Axiom 3 in the definition of a quasigroup Hopfπ-coalgebra toh⊗1α,∀α∈π,h∈H1. We now show 4) as follows:
for allh∈H1,
Δβ-1,α-1Sαβ*Δβ-1,α-1(h)=mβ-1⊗α-1(Δβ-1,α-1Sαβ⊗
Δβ-1,α-1)Δαβ,β-1α-1(h)=Δβ-1,α-1(Sαβ(h(1,αβ)))Δβ-1,α-1·
(h(2,β-1α-1))=Δβ-1,α-1(Sαβ(h(1,αβ))h(2,β-1α-1))=
Δβ-1,α-1(Sαβ*idβ-1α-1(h))=ε(h)Δβ-1,α-1(1β-1α-1)=
ε(h)(1β-1⊗1α-1)
and also, one has
Δβ-1,α-1*σHα-1,Hβ-1(Sα⊗Sβ)Δα,β(h)=
mβ-1⊗α-1(Δβ-1,α-1⊗σHα-1,Hβ-1(Sα⊗Sβ)Δα,β)Δβ-1α-1,αβ(h)=
h(1,β-1)Sβ(h(4,β))⊗h(2,α-1)Sα(h(3,α))=h(1,β-1)Sβ(h(3,β))⊗
ε(h(2,1))1α-1=h(1,β-1)Sβ(h(2,β))⊗1α-1=ε(h)(1β-1⊗1α-1)
Furthermore, for anyh∈Hαβ,
σHα-1,Hβ-1(Sα⊗Sβ)Δα,β(h)=ε(1β-1⊗1α-1)*σHα-1,Hβ-1(Sα⊗
Sβ)Δα,β(h)=(Δβ-1,α-1Sαβ*Δβ-1,α-1)*σHα-1,Hβ-1(Sα⊗Sβ)·
Δα,β(h)=(Sαβ(h(1,αβ))(1,β-1)h(2,β-1))Sβ(h(5,β))⊗
(Sαβ(h(1,αβ))(2,α-1)h(3,α-1))Sα(h(4,α))=
(Sαβ(h(1,αβ))(1,β-1)h(2,β-1))Sβ(h(4,β))⊗(Sαβ(h(1,αβ))(2,α-1)ε(h(3,1))) (by Axiom 4)=
(Sαβ(h(1,αβ))(1,β-1)h(2,β-1))Sβ(h(3,β))⊗Sαβ(h(1,αβ))(2,α-1)=
ε(h(2,1))(Sαβ(h(1,αβ))(1,β-1)⊗Sαβ(h(1,αβ))(2,α-1))=
ε(h(2,1))Δβ-1,α-1Sαβ(h(1,αβ))=Δβ-1,α-1Sαβ(h)
Thus,Δβ-1,α-1Sαβ=σHα-1,Hβ-1(Sα⊗Sβ)Δα,β,∀α,β∈π.
To show ②, we observe that
Sα(ab)=ε(b(1,1))Sα(ab(2,α))=
Sα(b(1,1)(1,α))(b(1,1)(2,α-1)Sα(ab(2,α)))=
Sα(b(1,1)(1,α))(ε(a(1,1))(b(1,1)(2,α-1))Sα((a(2,α))b(2,α)))=
Sα(b(1,1)(1,α))((Sα(a(1,1)(1,α))(a(1,1)(2,α-1)b(1,1)(2,α-1)))Sα·
(a(2,α)b(2,α)))=
Sα(b(1,α))((Sα(a(1,α))(a(2,α-1)b(2,α-1)))Sα(a(3,α)b(3,α)))=
Sα(b(1,α))((Sα(a(1,α))(a(2,1)b(2,1))(1,α-1))Sα·
((a(2,1)b(2,1))(2,α))=
Sα(b(1,α))(Sα(a(1,α))ε(a(2,1)b(2,1)))=
Sα(b(1,α))Sα(a(1,α))ε(a(2,1))ε(b(2,1))=Sα(b)Sα(a)

Finally, it is easy to obtain ③ and ⑤ by ①.
This completes the proof.
Corollary 1LetH=({Hα}α∈π,Δ,ε) be a quasigroup Hopfπ-coalgebra with the antipodeS={Sα}α∈π. Then,Sαis the unique convolution inverse ofidHα-1in the convolution algebra Conv(H,Hα-1), for allα∈π.
ProofTheorem 1① says thatSαis a convolution inverse ofidHα-1in the convolution algebra Conv(H,Hα-1), for allα∈π.
Fixα∈π. LetTαbe a right convolution inverse ofidHα-1in the convolution algebra Conv(H,Hα-1). For allh∈Hα,
Sα(h)=Sα*(idHα-1*Tα)(h)=
Sα(h(1,α))(idHα-1*Tα)(h(2,1))=
Sα(h(1,α))(h(2,α-1)Tα(h(3,α)))=ε(h(1,1))Tα(h(2,α)))=
Tα(ε(h(1,1))h(2,α)))=Tα(h)
and soTα=Sα.
Fixα∈π. LetTαnow be a left convolution inverse ofidHα-1in the convolution algebra Conv(H,Hα-1). For allh∈Hα, similarly we have,
Sα(h)=(Tα*idHα-1)*Sα(h)=
(Tα*idHα-1)(h(1,1))Sα(h(2,α))=
(Tα(h(1,α))h(2,α-1))Sα(h(3,α))=Tα(h(1,α))ε(h(2,1))=
Tα(h(1,α)ε(h(2,1)))=Tα(h)
and thus,Tα=Sα. Therefore,Sαis the unique convolution inverse ofidHα-1in the convolution algebra Conv(H,Hα-1), for allα∈π. This completes the proof.
Corollary 2LetHbe a quasigroup Hopfπ-coalgebra with the antipodeS={Sα}α∈π. Then,Δβ-1,α-1Sαβis the unique convolution inverse ofΔβ-1,α-1in the convolution algebra Conv(H,Hβ-1⊗Hα-1), for allα,β∈π.
ProofOne can see directly from the proof of Theorem 1(4) thatΔβ-1,α-1Sαβis a convolution inverse ofΔβ-1,α-1in the convolution algebra Conv(H,Hβ-1⊗Hα-1), for allα,β∈π. Fixα,β∈π. LetTβ-1,α-1be a right convolution inverse ofΔβ-1,α-1in the convolution algebra Conv(H,Hβ-1⊗Hα-1).
We writeTβ-1,α-1(h):=Tβ-1(h)1⊗Tα-1(h)2. For allh∈Hαβ, we have
Δβ-1,α-1Sαβ(h)=Δβ-1,α-1Sαβ*(Δβ-1,α-1*Tβ-1,α-1)(h)=
(Sβ(h(2,β))⊗Sα(h(1,α)))((h(3,β-1)⊗h(4,α-1))Tβ-1,α-1
(h(5,αβ)))=(Sβ(h(2,β))⊗
Sα(h(1,α)))((h(3,β-1)⊗h(4,α-1))(Tβ-1(h(5,αβ))1⊗
Tα-1(h(5,αβ))2))=Sβ(h(2,β))(h(3,β-1)Tβ-1(h(5,αβ))1)⊗
Sα(h(1,α))(h(4,α-1)Tα-1(h(5,αβ))2)=
ε(h(2,1))Tβ-1(h(4,αβ))1⊗Sα(h(1,α))(h(3,α-1)Tα-1(h(4,αβ))2)
(by Axiom 3)=
Tβ-1(h(3,αβ))1⊗Sα(h(1,α))(h(2,α-1)Tα-1(h(3,αβ))2)=
Tβ-1(h(2,αβ))1⊗ε(h(1,1))Tα-1(h(2,αβ))2=
ε(h(1,1))Tβ-1,α-1(h(2,αβ))=Tβ-1,α-1(h)
which implies thatΔβ-1,α-1Sαβ=Tβ-1,α-1. Fixα,β∈π. LetTβ-1,α-1be a left convolution inverse ofΔβ-1,α-1in the convolution algebra Conv(H,Hβ-1⊗Hα-1). In a similar manner, we can deduce by Axiom 4 thatΔβ-1,α-1Sαβ=Tβ-1,α-1.
Δβ-1,α-1Sαβis thus the unique convolution inverse ofΔβ-1,α-1in the convolution algebra Conv(H,Hβ-1⊗Hα-1), for allα,β∈π. This completes the proof.
Corollary 3According to Theorem 1①, each quasigroup Hopfπ-coalgebra is both the first alternative and the second alternative.
Corollary 4LetH={Hα}α∈πbe a quasigroup Hopfπ-coalgebra. Then, {α∈π|Hα≠0} is a subgroup ofπ.
ProofSetG={α∈π|Hα≠0}. Sinceε(11)=1k≠0, we first have 11≠0,i.e.H1≠0, and so 1∈G. Then, letα,β∈G. Using Axiom 2, one can also see thatΔα,β(1αβ)=1α⊗1β≠0. Then, 1αβ≠0 and soαβ∈G. Finally, letα∈G. By Theorem 1③,Sα-1(1α-1)=1α≠0. Thus, 1α-1≠0 and hence,α-1∈G. This completes the proof.
Theorem 2LetHbe a quasigroup Hopfπ-coalgebra. Then, for anyα∈π,Sα-1Sα=idHαif H is commutative or cocommutative.
ProofFor anyα∈π. Leth∈Hα. If H is commutative, we have
Sα-1Sα(h)=Sα-1Sα(h(1,α)ε(h(2,1)))=
Sα-1Sα(h(1,α))(Sα-1(h(2,α-1))h(3,α))=
Sα-1(Sα(h(1,1)(1,α)))(Sα-1(h(1,1)(2,α-1))h(2,α))=
Sα-1(S1(h(1,1))(2,α-1))(S1(h(1,1))(1,α)h(2,α))=
(h(2,α)S1(h(1,1))(1,α))Sα-1(S1(h(1,1))(2,α-1))=
ε(S1(h(1,1)))h(2,α)=ε(h(1,1))h(2,α)=h
It follows thatSα-1Sα=idHα.
IfHis cocommutative, we find that
Sα-1Sα(h)=Sα-1Sα(h(1,α)ε(h(2,1)))=
Sα-1Sα(h(1,α))ε(h(2,1))=
Sα-1Sα(h(1,α))(Sα-1(h(2,α-1))h(3,α))=
Sα-1(Sα(h(1,1)(1,α)))(Sα-1(h(1,1)(2,α-1))h(2,α))=
Sα-1(S1(h(1,1))(2,α-1))(S1(h(1,1))(1,α)h(2,α))=
Sα-1(S1(h(1,1))(1,α-1))(S1(h(1,1))(2,α)h(2,α))=
ε(S1(h(1,1)))h(2,α)=ε(h(1,1))h(2,α)=h
It also follows thatSα-1Sα=idHα. This completes the proof.
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Coupling dimensions of human resource archetypes and organizational learning modes
- Min-max fuzzy model predictive tracking control of boiler-turbine system for ultra-supercritical units
- Firm review revelation policy considering social ties among consumers
- Expansion performance and self-stressing behavior of CFST columns considering concrete creep and shrinkage effect
- A fault feature extraction method of gearbox based on compounddictionary noise reduction and optimized Fourier decomposition
- Effect of carbonation-drying-wetting on durability of coral aggregate seawater concrete
