基于温度控制的恒温箱控制系统性能分析

朱浩楠 李 琪 张宏锐

（东北林业大学机电工程学院，黑龙江 哈尔滨150040）

1 恒温箱控制系统工程背景

从20 世纪50 年代开始，温度控制界逐渐发展了串级控制、前馈控制、Smith 预估控制、比值控制、选择性控制和多变虽解耦控制等策略与算法，称为复杂控制。他们在很大程度上满足了复杂过程工业的一些特殊控制要求。他们仍然以经典控制理论为基础，但是结构与应用上各有特色，而且目前仍在继续改进与发展。随着控制技术的不断发展及现代工业的发展,在现代工农业生产以及科研实验的许多场合都需要及时准确地获取温度信息,并完成对温度的预期控制,而且对温度控制稳定性和精度的要求越来越高,所以必须在控制思想的基础上研究出有效的控制策略。

2 恒温箱控制系统工作原理分析

恒温箱控制系统由如下几个部分组成：

2.1 恒温箱：由箱体和加热电阻丝组成，是控制系统的被控对象，恒温箱内的温度T为被控制量。

2.2 热电偶：温度测量元件。测量温度值将温度信号转换为支撑比例变化的电压信号输出，其工作特性为uT=KT。

2.3 分压器：由直流电源和可变变阻器组成。当恒温箱内的温度T=T0 时，电偶的输出电压uT=KT=uT0，对应被控制量的理想值。

2.4 放大器：由电压、功率放大器组成，称为放大元件。放大器的等效放大倍数为K=K1K2，其工作特性为ua=KΔu。

2.5 执行机构：由直流伺服电动机、减速器和调压器构成，根据被控制量的变化要求，实现对控制信号自动调整。

3 恒温箱控制系统数学模型建立

自动控制系统的数学模型有：微分方程、传递函数、系统框图、信号流图、根轨迹图、频率特性曲线。先根据恒温箱温度控制系统的各个部分建立其微分方程、传递函数、系统框图的数学模型，再利用基本串并联、基本反馈的等效变换和相加点、分支点间的移动进行系统框图的等效化简。至于根轨迹图、频率特性曲线将在后续章节中进行系统性能的分析中呈现。

系统建模的关键在于求取系统的传递函数，将各个环节等效为对应的典型环节或直接求取该环节的传递函数，其参数为工程中实际参数，即查阅文献得知。最后由各环节传递函数和各环节关系得出传递函数。在这样的大体思路下，我们先来分析各个环节的传递函数。

3.1 热电偶：在控制系统中,热电偶用作为信号变换装置，可以组成温度检测器，由于恒温箱温度变化在很小的范围内变化，可以认定为输出电压与电偶温度成线性变化，这样热电偶的温度增量T

作者简介：朱浩楠（2000，05-），男，汉族，籍贯：陕西西安，本科在读，研究方向：电气工程及其自动化。（t）与输出电压u（t）的关系曲线在进行理论分析时可以用直线近似，于是可得输出电压为u（t）=K0T（t）。

3.2 电压、功率比较放大器：电压比较放大器和功率放大器是比较电路和一部分放大元件的总和，其功能是把被控制量和给定量进行比较，然后进行放大。

3.3 直流伺服电动机：恒温箱采用直流伺服电机是执行元件，使其被控量发生变化。在一般情况下，对于调速范围不大、动态响应要求不高的系统，可以使用普通直流电动机。对于调速范围大、动态响应要求快的系统，特别是伺服系统（随动系统），则应采用直流伺服电动机。

3.4 减速器：减速器的作用是使直流伺服电动机与调压器之间获得合适的速比配合。

3.5 调压器：调压器作用是根据ua信号的变化带动调压器的调整手柄移动，使调压器的输出电压u 改变，从而改变加热电阻丝的电压，实现恒温箱的温度调整。

4 系统性能分析研究

4.1 系统性能时域分析研究

从工程实际考虑，我们知道恒温箱控制系统的时间惯性比较大，调节时间比较长。通过查阅资料得到直流伺服电机的时间常数Tm一般为十几毫秒到几十毫秒之间。因此，我们取时间常数为Tm=0.1s。对于研究的恒温箱系统来说是一个二阶系统，因此阻尼比ξ 为欠阻尼状态，一般选择为0.4～0.8 之间，先选用一个实际中阻尼比为0.76 的恒温箱系统进行计算。因系统的开环传递函数为

计算得到ωn=6.57rad/s。系统的开环增益为K=4.32（rad/s）2

根据劳斯判据内容：①若劳斯阵列第一列元素都为正，则系统稳定。②若劳斯阵列第一列元素出现0，则系统一定不是稳定的。③若特征方程缺项或者有负系数，则系统一定不是稳定的。

由上面的劳斯阵列可知，该系统是稳定的（因为第一列元素全为正）。

4.1.2 系统准确性分析研究。由以上分析已知，系统开环传递函数为

4.2 系统性能根轨迹分析研究

4.2.1 系统稳定性分析研究。假设系统的开环传递函数为

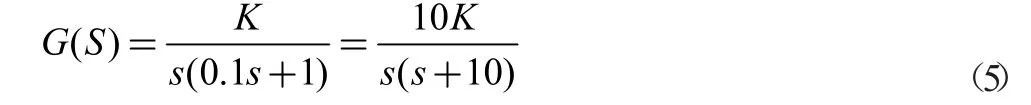
当根轨迹增益从零变化到无穷大时，所有闭环极点都不会穿越过虚轴进入到s 右半平面，即当k＞0 时，无论根轨迹增益k 为何值，闭环系统都是稳定的。

4.2.2 系统准确性分析研究。因在时域分析法中利用“静态误差系数法”求解的稳态误差，故在本小节试利用“动态误差系数法”来求解稳态误差。

本系统的等效开环传递函数为

则系统的稳态误差为

由此可见，利用“静态误差系数法”求解的稳态误差等于利用“动态误差系数法”来求解稳态误差。

4.3 系统性能频率特性分析研究

4.3.1 系统稳定性分析研究

4.3.1.1 根据奈氏判据：若闭环系统在[s]右半平面有P 个开环极点，当ω 从-∞变化到+∞时，奈奎斯特曲线G（jω）H（jω）对（-1，j0）点的包围周数为N（N＞0 为逆时针，N＜0 为顺时针），则系统在[s]右半平面上的闭环极点的个数为Z=P-N。若N=0，则闭环系统稳定，否则系统不稳定。G（jω）H（jω）对（-1，j0）点的包围周数为0，闭环系统在[s]右半平面有0 个开环极点，即P=0。∴Z=P-N=0，所以可得系统是稳定的。

可以看出，剪切频率ωc=4.01，相角裕度γ=68.15°；相位穿越频率为ωg=∞，系统的幅值裕度Kg=∞。对于开环稳定的系统，欲使闭环稳定，其相位裕度必须为正，即γ>0，一个良好的控制系统通常要求30°～60°之间。由此可见系统稳定，并且其相对稳定裕度相当好。但实际的相角裕度γ=68.15°并不在理想的30°～60°之间，故该系统需要添加一个滞后校正元件。

4.3.2 系统准确性分析研究。由“三频段”说法可知：①系统的低频段主要是比例积分或纯微分环节在起作用，因此低频段反应的是系统的稳态性能。低频段的斜率陡、增益大表明系统的稳态精度高。②系统的中频段是指L（ω）在剪切频率ωc附件的区段，若想使闭环系统稳定并且有足够的相位裕度，那么过ωc的斜率最好为-20dB/dec，通常取中频段斜率为-20dB/dec 并且具有一定的宽度来达到满意的平稳性，从而来提高系统的快速性，中频段反应了系统的动态性能和稳定性。③高频段则对系统性能影响不大，它往往反映的是系统对高频噪声的抗干扰能力。

5 结论

由以上恒温箱自动控制系统的性能分析过程可以看出，在面对任何一个自动控制系统的分析设计的宏观思路都是相同的。即先根据劳斯阵列分析稳定性、再根据稳态误差分析稳定性、最后根据动态性能分析快速性。而又可结合根轨迹法、频率特性分析法来对以上性能进行验证。若分析出来的系统性能不满足实际工程工作要求，则还需对系统需要进行相应校正，不同的系统还根据其所需哪一方面的性能需求而需要不同的校正方式。综上，以上的恒温箱自动控制系统的性能分析方法适用于绝大多数实际工程中的自动控制系统分析，因此具有推广价值。