硬岩深埋隧道开挖围岩损伤区的有限元分析

孙晓飞

（中交路桥华南工程有限公司，广东 中山528403）

1 概述

岩体是一种非连续、非均质的各向异性材料。在人工开挖作用下，岩体将发生复杂的变形和失效模式，进而造成岩体的物理和力学属性发生显著的变化。近年来，随着水利、水电、能源资源、核废料存储、CO2封存等建设需求，地下工程开挖逐步向深部转移[1]。深埋隧道开挖过程中将造成原岩应力释放，应力重新分布将造成开挖壁面围岩产生微裂纹。这些微裂纹在外力作用下扩展并汇聚，最终发展成宏观裂隙，部分岩体脱离围岩整体形成围岩开挖损伤区。开挖损伤区深度和范围的确定对围岩支护方案设计具有重要的影响作用。此外，开挖造成的围岩损伤将增大围岩的渗透性，形成流体泄露的潜在路径。因此，开挖损伤区形状和范围的预测分析是地下储库稳定性最为关键的问题之一。

在过去的50 年，数值模拟技术在岩体力学领域快速发展，已成为研究岩体力学的一种有效手段。2001 年，Cundall 提出离散单元法来模拟岩体失效过程[2]。2002 年，Hajiabdolmajid 等采用粘聚力弱化- 摩擦强化模型成功地模拟再现了Mine-by 隧道开挖损伤区的形状和范围[3]。2007 年，Shin 等考虑岩石细观各向异性特点提出了岩石晶粒模型，用于模拟分析花岗岩开挖损伤区的形状和范围。一些学者采用有限元- 离散元耦合方法研究岩体在准静态和动态荷载作用下裂纹萌生、扩展和汇聚机理。可将国内外岩体力学数值模拟技术分为三大类：（1）连续方法，包括边界元、有限元和有限差分法；（2）非连续方法，包括离散元和非连续变形分析法DDA；（3）混合耦合方法，包括边界元- 离散元耦合、有限元- 边界元耦合、有限元- 离散元耦合以及其他的耦合计算方法。离散元法在模拟分析岩体失效方面具有独特的优势，可以再现裂纹萌生和扩展的渐进过程。但离散元法存在一些不足之处，如繁琐的细观参数标定和低计算效率。与离散元相比，连续方法在分析开挖损伤区方面比较简单、灵活。鉴于Phase 2 有限元软件涵盖众多常用岩石本构模型，本文采用Phase 2 模拟分析硬岩深埋隧道开挖围岩损伤区的形状和范围。

为有效指导实际开挖工程，应确保数值计算结果的可靠性，因此应考虑合适的岩体本构模型和实际的隧道断面不规则形状等因素。本文首先分析了在高应力作用下岩体的失效过程；其次以加拿大Mine-by 隧道室内实验为模型，分别采用弹-脆- 塑模型EBP、粘- 脆- 摩擦模型CBF 和损伤初始剥落模型DISL 三种本构模型模拟分析Mine-by 隧道开挖引起的围岩损伤区，三种模型的计算结果表明了DISL 模型的优越性；最后考虑到Mine-by 隧道断面的非规则性，建立了非规则隧道断面模型，研究几何边界条件对隧道开挖损伤区的影响作用。

2 脆性岩体力学本构模型

脆性岩体的失效过程可以划分为以下三个关键阶段：（1）达到起裂应力σci时，在局部拉应力作用下造成微裂纹萌生，且微裂纹沿着最大压应力方向扩展；（2）达到裂纹损伤应力σcd，裂纹相互作用，不稳定扩展，岩体发生剪胀行为；（3）达到峰值应力σf，裂纹密度持续增大，致使宏观裂纹或剪切带形成，岩体失效。以上脆性岩体失效的三个阶段可通过微震监测、声波测试、多点传感器测试以及钻孔电视等方式获取，且这三个阶段是数值模拟分析岩体失效的关键所在，也是评判所选岩体本构模型可行性的标准。

2.1 应变软化模型EBP

应变软化模型重在强调低应力环境中峰后岩体力学属性的弱化特征，故应变软化模型主要适用于浅部地下工程开挖以及软岩开挖工程。应变软化模型的脆性失效行为可通过弹- 脆- 塑模型描述，见图1 所示。

2.2 粘- 脆- 摩擦模型CBF

标准柱体岩样低围压力学试验结果表明，拉裂纹平行于最大压应力方向张开，进而削弱法向应力的有效传递，裂隙面的有效压应力为零。随着裂纹的增长，裂纹的粘聚长度逐渐减小。当裂纹发生相互作用，微裂纹相互连接贯通时，将形成宏观裂纹或者剪切带，摩擦强度将随着粘聚力的减小而减小。1977 年，Martin 提出了岩体粘- 脆- 摩擦模型模拟岩体脆性失效特征。粘- 脆- 摩擦模型表明当偏应力（σ1-σ3）大于1/3 倍单轴抗压强度（UCS）时，岩体发生屈服，同时伴随着粘聚力和摩擦强度的弱化。低围压时，粘聚力衰减幅度最大。粘- 脆- 摩擦模型的强度包络线在摩尔应力图上的表示见图2 所示。

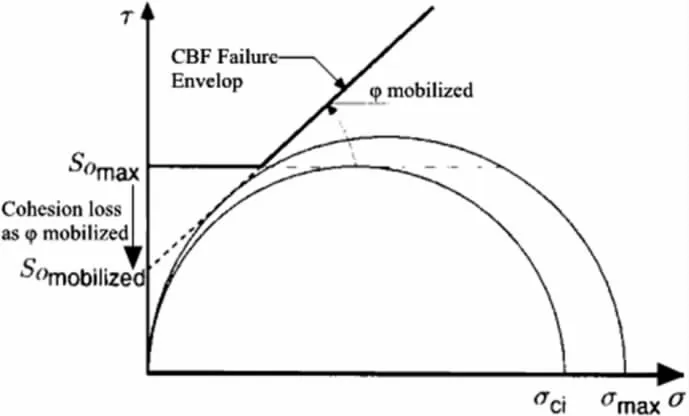
图2 粘- 脆- 摩擦模型

2.3 损伤初始剥落模型DISL

2003 年，Diederichs 在广义Hoek-Brown 准则基础上提出了用于描述岩体脆性剥落特征的损伤初始剥落模型DISL，该模型与粘- 脆- 摩擦模型的最大不同在于损伤初始剥落模型DISL可描述低围压变化至高围压过程中岩石发生的不同脆性力学特征。开挖造成应力重分布后大于初始应力时，开挖断面将会沿着最大主应力方向发生层状剥落损伤破坏，岩体呈应变软化特征。在高围压作用下，岩体剪切失效，且残余强度大于峰值强度，即随着围压增大，距离开挖断面较远的深部岩体在初始损伤之后将发生应变硬化行为。广义Hoek-Brown 准则可表示为：

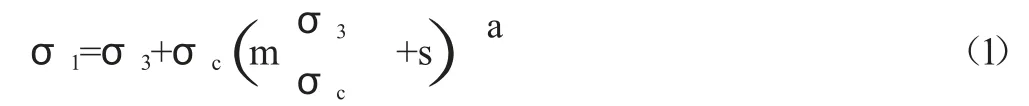
式（1）中，σc为完整岩石的单轴抗压强度，a 为岩体常数，m和s 为材料常数，分别反应岩体的摩擦强度和粘聚力强度。在Hoek-Brown 准则中，粘聚强度的衰减可通过s 的减小得以体现，摩擦强度的衰减可通过m 的增大得以体现。损伤初始剥落模型DISL 见图3 所示，其中初始损伤强度包络线由峰值参数ap，mp，sp定 义，剥 落 强 度 线 由 残 余 阶 段 参 数ar，mr，sr定 义。Diederichs 的研究表明，对于初始损伤强度包络线ap可取0.25，对于剥落强度线ar可取0.75，岩体常数a 主要控制强度包络线的曲率。

3 Mine-by 隧道开挖数值模型

3.1 Mine-by 隧道

本文采用上述三种岩体本构模型模拟分析Mine-by 隧道开挖，实际工程中在隧道开挖前安装了许多先进的地质机械仪器用以监测开挖引起的损伤和岩体力学行为，以Read 和Martin的现场监测结果为依据，评判数据模拟结果的可靠性。

Mine-by 隧道断面直径3.5m，长420m，并于1992 年1 月至7 月开挖。为了避免爆破掘进对围岩的损伤破坏，采用沿周边线钻孔机械破岩法掘进，这极大便利了对开挖过程中隧道围岩脆性破坏的监测。现场观测表明，随着隧道掘进，破坏沿径向发生，最终在最大切向应力区域形成V 形切口。图4 为隧道断面顶部破坏区的形状，其中V 形切口的半径深度为隧道断面半径的1.3 至1.5 倍。由于隧道底部总被碎石充填，所以隧道底部损伤区的深度并未测量。

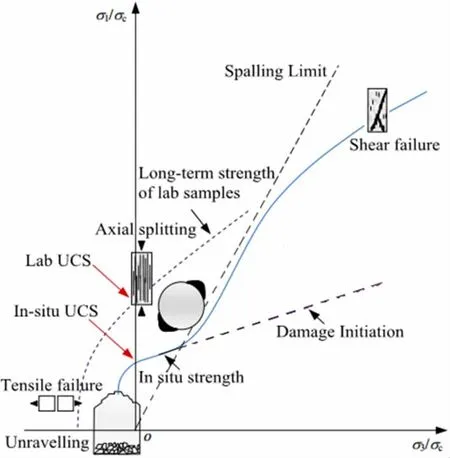
图3 损伤初始剥落模型

3.2 Mine-by 隧道开挖模型

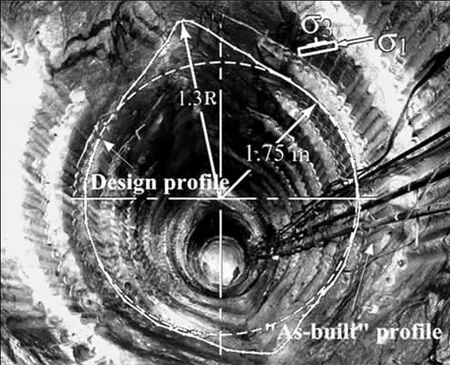
图4 Mine-by 隧道的设计断面和损伤断面

由于Mine-by 隧道采用机械破岩法掘进，隧道断面极其不光滑，见图4 所示。隧道断面几何不规则处极易发生应力集中现象，进而导致围岩损伤破坏。本文建立了圆形和一系列半圆隧道断面模型用于研究边界几何形状对开挖损伤区的影响作用，数值模型各个侧面施加相应方向的位移约束条件。Perras 表明单元尺寸为开挖半径的0.02 倍时，模型可有较高的计算效率，且能大大弱化单元尺寸对损伤区形状和范围的影响作用，故本文模型中隧道开挖断面3m 区域内的单元尺寸均小于0.03m。模型网格划分见图5 所示，光滑断面模型采用径向渐变网格划分技术，粗糙不规则断面模型采用两种网格- 距开挖断面3m 范围内的圆形区域采用0.03m 的网格，向外区域采用径向渐进网格。

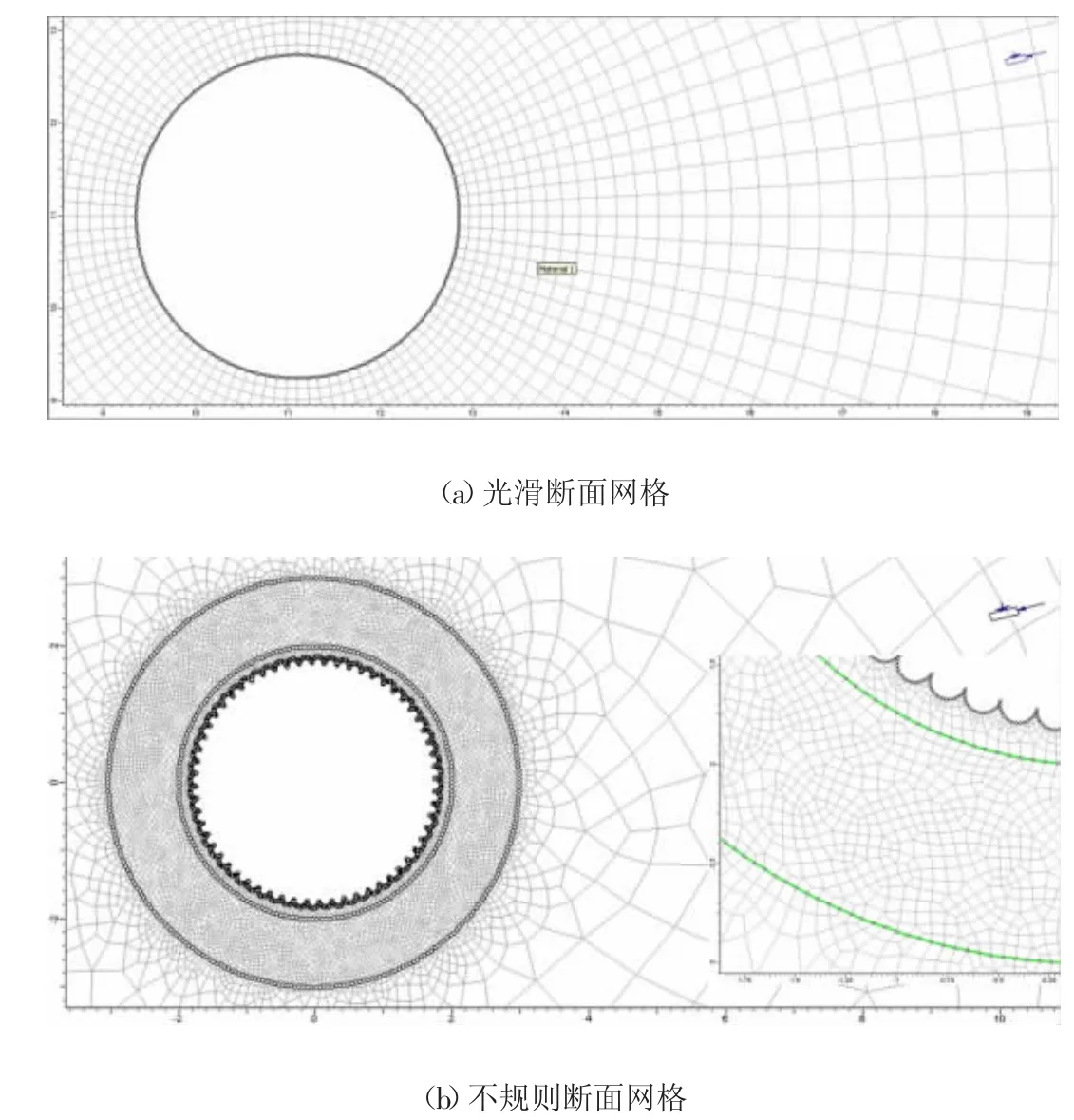
图5 隧道开挖断面模型网格

Mine-by 隧道在块状花岗岩中掘进，平行于第二主应力（σ2=45MPa）方向开挖，原位最大主应力和最小主应力分别为σ1=60MPa、σ3=11MPa，且分别与水平、垂直方向的夹角均为15°。围岩弹性模量60GPa，泊松比0.2，围岩的强度参数见表1所示。（Perras et al.,2016;Diederichs,2007）

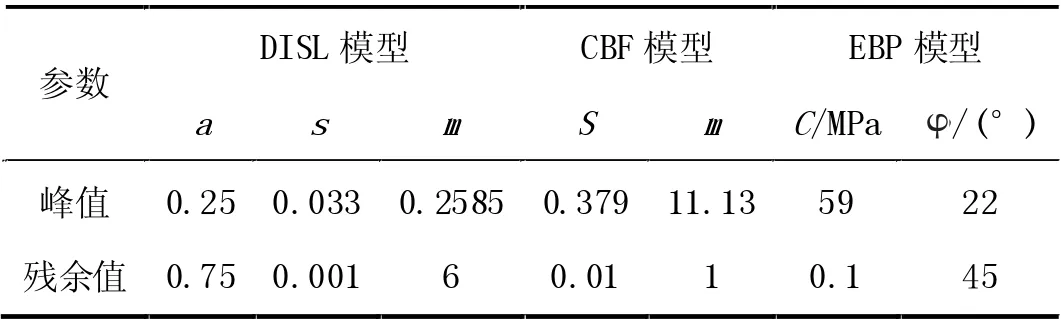
表1 Mine-by 隧道围岩强度参数

4 Mine-by 隧道开挖数值模型结果分析

4.1 光滑断面数值模拟结果分析

如图6（a）所示，采用弹- 脆- 塑模型的隧道断面围岩在顶部和底部并未形成V 字切口破坏，该特征符合2.1 节所述应变软化模型不适用于深部硬岩脆性破坏。光滑断面粘- 脆- 摩擦模型CBF 模型中开挖断面的最大切应力和最大主应力分别为165 MPa 和179 MPa，约为围岩单轴抗压强度的0.8 倍，围岩实际将会发生屈服，然而模型并未发生损伤破坏，这与现场观测相悖。光滑断面DISL 模型的隧道损伤区计算结果见图6（b）所示，模型顶部损伤区深度约为0.48 m，与实际损伤区深部相比偏小。此外，损伤区呈矮胖型，与实际V 字切口高瘦型特征不符。究其原因主要在于光滑断面模型忽略了实际不规则断面几何变化引起的局部应力集中效应，这对V 字切口的形成具有重要的影响作用。

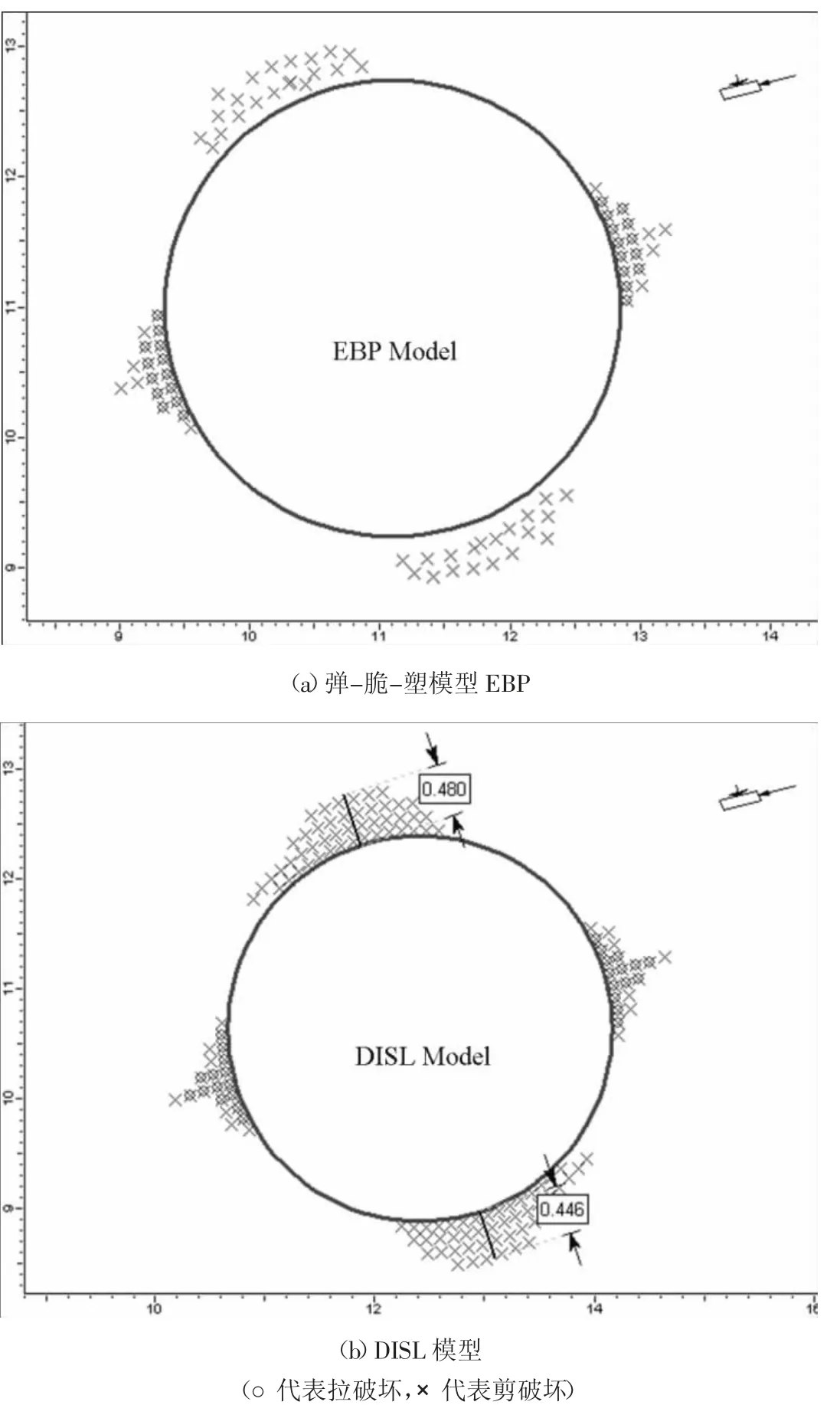
图6 光滑断面损伤区模拟结果

4.2 不规则断面数值模拟结果分析

不规则断面隧道损伤区模拟结果见图7 所示，与实际损伤区相比，图7（a）中损伤区跨角较大，图7（b）中损伤区跨角和深度均较小，表明弹- 脆- 塑模型EBP 高估了损伤区范围，而粘- 脆- 摩擦模型CBF 低估了损伤区范围。图7（c）为DISL 模型损伤区模拟结果，损伤区顶部深度约为0.544 m、跨角68°，损伤区模拟结果和实际破坏的几何尺寸吻合。

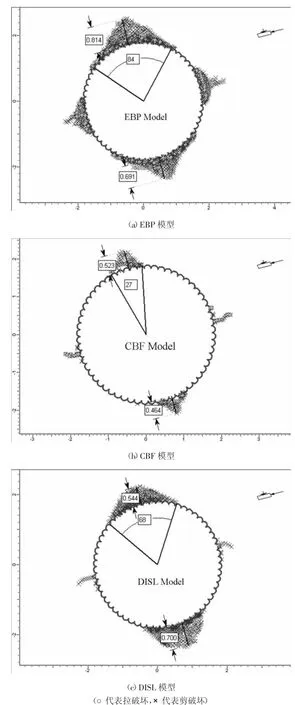
图7 不规则断面损伤区模拟结果

图8 显示了隧道中心至V 字切口中心路径上的主应力分布特征。靠近隧道断面的损伤区部分处于卸荷状态，位于此部位的围岩几乎不承受载荷，该部位以拉剪损伤为主。损伤区尖端只发生剪切损伤，此部位具有较高的残余强度。EBP 模型的V字损伤区前端最大最主应力位于距隧道中心的2.65 m 处，远高于其他两个模型。EBP 模型描述的是粘聚强度和摩擦强度同时衰减至蜂后残余值，导致损伤区具有较低的承载能力，因此最大主应力所在处不断向深部转移，与其他两个模型相比，损伤区范围最大。对于CBF 和DISL 模型，脆性失效通过粘聚力弱化和摩擦损失得以体现，损伤区围岩仍有较高的残余承载能力，故最大主应力所在处距离隧道断面较近。此外，图8 表明，CBF 模型的最大主应力值远大于DISL 模型。CBF 模型的输入参数是基于摩尔库伦准则确定的粘聚力和摩擦角，这两个参数并未考虑岩体尺寸以及原位节理裂隙特征。相反，DISL 模型输入参数的确定是结合地质指标GSI 和室内完整岩石的单轴抗压强度确定的，更能准确反应原位岩体的力学属性。因此，DISL 模型中围岩表现更低的承载能力。

5 结论

5.1 光滑断面模型不能够准确再现实际隧道V 字切口损伤区特征，应考虑不规则几何断面特征对损伤区的影响作用。

5.2 不规则断面模型中，EBP 模型损伤区跨角84°大于实际70°；CBF 模型损伤区跨角27°、深度0.523 m 均小于实际损伤区特征；DISL 模型损伤区跨角68°、深度0.544 m 均几何吻合实际损伤区特征，DISL 模型较其他两者相比最能准确反应损伤区特征。

5.3 Hoek-Brown 准则较Mohr-Coulomb 准则更适用于描述岩体强度特征。