一种水下多普勒估计的算法与研究
2021-04-24赵梓琛张轩野郭佳明
赵梓琛 张轩野 郭佳明
(哈尔滨工程大学,黑龙江 哈尔滨150000)
在水声通信中,因为收发双方多数会存在相对运动并且海洋表面会有波动等,使得在数据的接收端会发生多普勒频移现象[1],多普勒频移现象在时域上会使得数据帧进行伸展或者收缩,从而造成接收端的同步与跟踪过程具有极大的无误差,甚至会使接收端无法进行正常的工作,导致通信系统的误码率增大。在我国,水声通信中多普勒估计与补偿方法[2]的研究工作已经成为我国水声工程领域中面临的巨大挑战。
1 主要工作
信号在经过高斯信道和真实水声信道之后,利用两种算法即五点三次平滑算法、加权平均算法,对多普勒频移进行估计与补偿,并分别进行了比较,给出一种较为准确的多普勒估计与补偿方法,最后给出了与不对多普勒因子进行估计情况下的对比,给出效果较好的方法。
2 高斯信道和真实信道下仿真结果
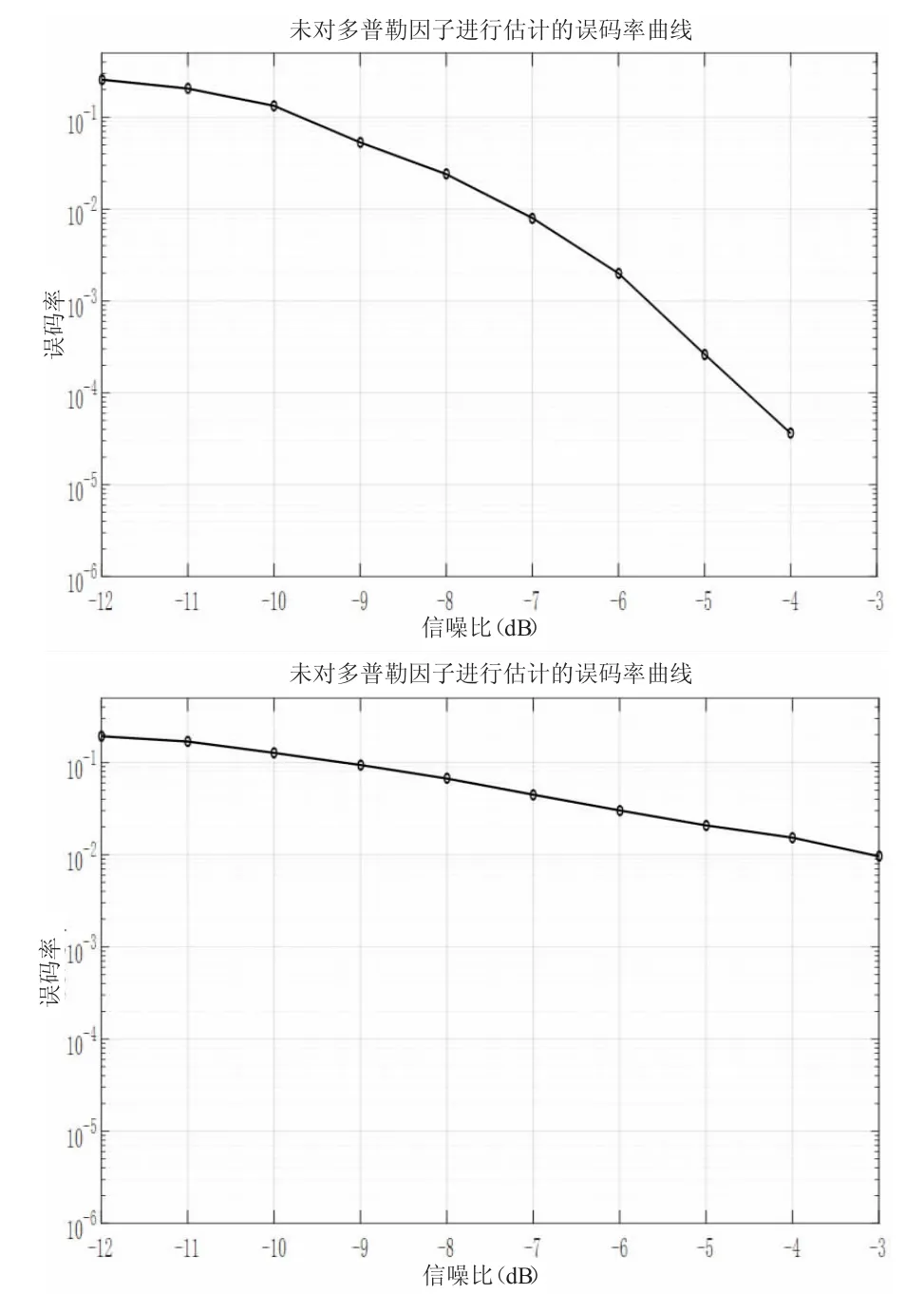
图1 未对多普勒因子进行估计的误码率曲线(左侧为高斯信道,右侧为真实信道)
本设计中的通信系统经过两个不同信道,分别为高斯信道以及真实水声信道,对接受的信号进行同步过程过后,直接找到LFM同步头尾部位置,并对接收到的训练序列以及Packet 序列中的码片进行FFT,得到的频率与本身频率进行对比,得到多普勒因子,不做估计,只取均值之后就解调信息序列,在不同信噪比下,循环10000 次,得到误码率曲线如图1 所示。
3 多普勒估计与补偿简介
声波在传播过程中,如果接收方和声源即声音发射处存在相对运动,这时候接收到的声音与发射本身的声音相比,频率会发生改变,这种现象叫做多普勒频移现象。由于声波在水中的传播速度与无线电在陆地上传输相比是微乎其微的,并且水声领域中,通信信号所覆盖的频带范围相对较窄,这两点导致,相较于陆地无线电通信,多普勒频移现象在水下通信中影响更为严重。[3]
另外,多普勒效应的影响不仅是频率偏移,还有压缩或拉伸信号。如何降低多普勒频移的影响是水声通信领域迫切需要解决的问题。为了使通信系统能够精确的知道发射端传输的信息,多普勒因子估计方法[4]成为了水声通信中非常重要的一部分。
在估计多普勒因子的过程中,本文通过采用三点取最大值,经过对信号进行FFT 之后,会得到横轴为频率,纵坐标为幅度的图形,在这个图形中,由于FFT 算法,不能知道这段信号的最大频率,因此本文采用三点坐标抛物线拟合法求得一段信号的准确峰值。具体方法如下:
首先确定临近最大值的三个点,设为(f1,y1)、(f2,y2)、(f3,y3),之后设抛物线方程为:y=ax2+bx+c,将这三个点带入方程会得到以下式子:

本文多普勒估计方法是在找到LFM的同步头位置之后,用不准确的(原来的)点数作为FFT 算法的开始位置,做训练序列以及PACKET 序列中码片的FFT,之后与原来的频率进行对比,得到了多普勒因子曲线。此种方法没有消除多普勒扩展,误差较大。所以本文进行了优化,在找到LFM同步头之后,先将64位训练序列[5]的多普勒因子估计出来,之后用alpha 估计后方packet 序列中一个码片的多普勒因子(相当于重新同步过程),之后用新估计出来的多普勒因子去估计下一个码片,以此类推。最后取所有估计出来的多普勒因子中值作为最后解调的多普勒因子。
多普勒补偿流程图如图3 所示:
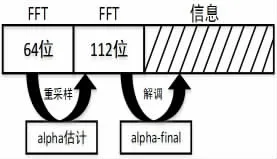
图3 多普勒补偿流程图
4 多普勒估计方法
4.1 加权平均滤波算法。依据时间进行顺序排列,选取一样的变量的几个观测值,随后利用时间序列来作为权重,计算出观测值的加权算术平均值。这个算术平均值被用作预测未来期间该变量的值,这种方法被称为加权平均滤波算法[6]。

4.2 五点三次平滑算法。五点三次平滑算法的原理是在原始数据中取相邻的5 个点,拟合出一条曲线,拟合三次,将最后的结果作为经过滤波之后的结果,原理类似于Savitzky-Golay滤波器[7]。不同点在于Savitzky-Golay 滤波器没有考虑前两个点与后两个点,本文设计的这个算法把没考虑的几个数据值的拟合结果给推导并显示出来。
以五点三次平滑算法为参照,演算推导出滤波公式。首先定义一组以2n+1 为等距节点的数组X-n,X-n+1,…,Xn-1,Xn,Y-n,Y-n+1,…,Yn-1,Yn是 分 别 对 应 的 实 验 数 据,t-n=-n,t-n+1=-n+1,tn-1=n-1,tn=n,用m 次多项式来进行实验数据的估计。其中拟合多项式为:

当n=2,m=3 时候,得到一个具体方程组,由此求出系数a0、a1、a2…am

其中前面两点分别用公式(10)、(11)来平滑,最后两点用公式(13)、(14)来平滑,其余的均用公式(12)表示。
4.3 两种算法的仿真与对比
高斯信道下的仿真与实现:
下面分贝采用加权平均滤波算法、五点三次平滑算法进行估计,由于加权平均算法的机理原因,无法得到前后部分码片的多普勒因子,因此还是采用2 倍因子数据来进行平滑拟合,得到的结果如图4:
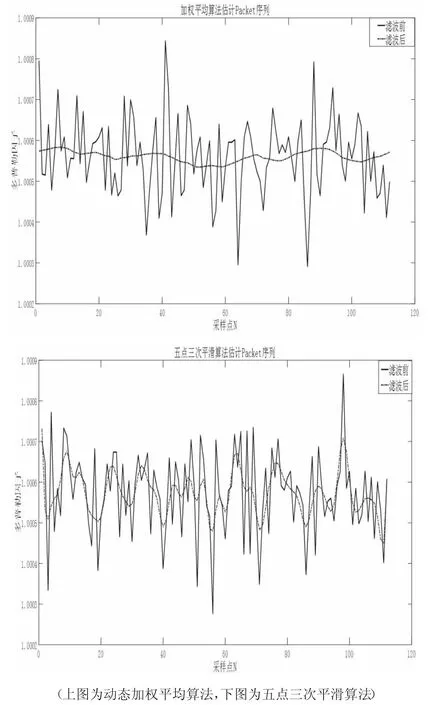
图4 多普勒因子估计仿真结果
5 结论
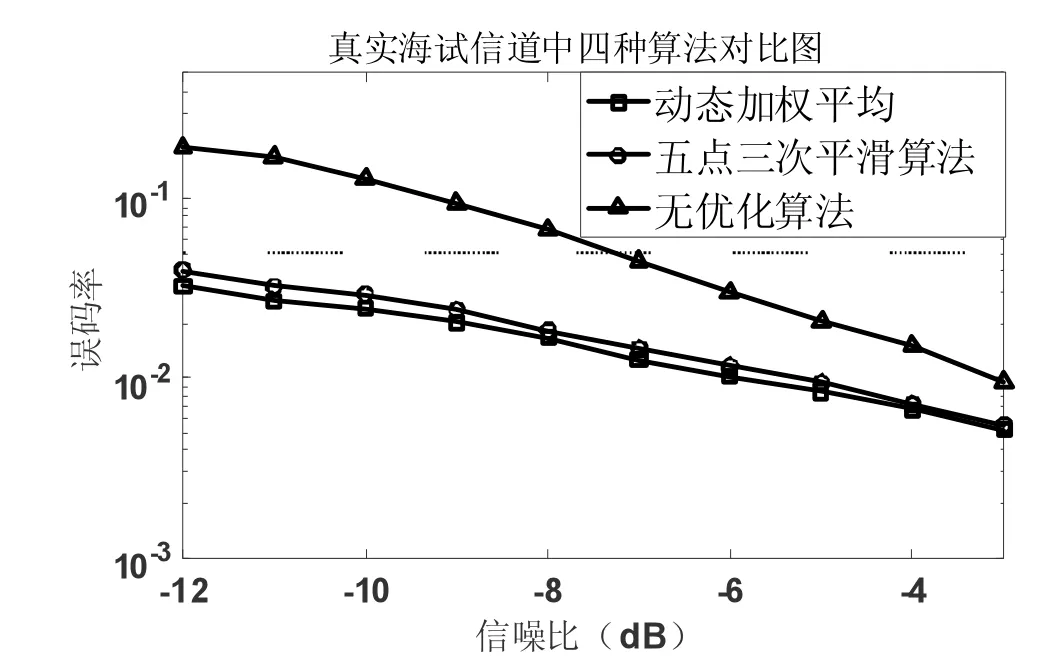
图5 误码率仿真结果
在水声通信中,多普勒估计与补偿工作一直是一个难题,随着研究的不断深入,很多学者已经做出了不少效果很好的估计与补偿方案,本课题针对多普勒因子采用两种算法对多普勒因子进行了估计与优化,用实际数据处理加以验证,都得到了良好的效果。本课题的主要内容有:
(1)介绍了目前水声通信工作中,多普勒估计与补偿的基本原理及研究意义。
(2)在多普勒因子估计与补偿的过程中,通信系统经过两个不同信道,即高斯信道、真实水声信道之后,采用五点三次平滑算法和加权平均算法,这几种算法通过误码率曲线来比较算法性能的好坏,同时采用计算与比较MSE 来判断算法的优劣,最后发现加权平均算法的效果最好。
