基于多尺度窗口的自动调焦算法

张 驰，韩冬艳，冉 迪，胡楷钰

(1 陆军装备部驻西安地区军事代表局驻西安地区第七军事代表室，西安 710065；2 西安现代控制技术研究所，西安 710065；3 陆军装备部驻西安地区军事代表局驻南阳地区第一军事代表室，河南南阳 710032)

0 引言

基于图像处理的自动调焦技术可高效、准确对主体目标进行聚焦，在军事、民用领域有着广泛应用。其核心为采用某种评价函数对图像清晰度进行量化，再通过调焦搜索算法及动力机构驱动可变镜头组对物距或像距进行调整，最终实现成像系统准确聚焦[1-6]。

由于求解图像全局清晰度评价函数所需计算量较大，故实际应用中常采用适当的调焦窗口来缩减求解范围，以减少计算时间[7-9]。常见调焦窗口构建算法有中心区域法、非均匀采样法、多区域选择法等，其共同特点是选取包含成像主体的局部区域作为求解范围，在保持清晰度函数趋势与全局计算一致的前提下以更少的计算量搜索到最佳聚焦位置。

文中提出一种基于多尺度窗口的分段式自动调焦算法，第一阶段利用小尺寸调焦窗口，在清晰度函数与全局近似的情况下，快速寻找到局部聚焦位置；以该位置作为第二阶段调焦的起点，增大窗口范围，再以少量步数搜索到全局聚焦位置。实验表明，该方法可有效降低图像清晰度计算量，提升自动调焦的实时性。

1 清晰度评价函数

清晰度评价函数是衡量聚焦是否准确的核心。理想的清晰度曲线要求满足单峰性、无偏性[10-12]。

现有的评价函数主要分为空域、频域、信息学三类。其中频域评价函数的计算复杂度较高，实时性不易满足；基于信息学的评价函数对图像聚焦点的分辨力相对较弱；而空域类函数一般采用求解灰度梯度、提取边缘等，可以相对低的复杂度取得较好的清晰度分辨力，在实际工程中使用较为广泛。

2 调焦窗口构建算法

基于全局求解评价函数的计算量较大，不利于整个调焦系统的实时性，一般构建某种调焦窗口，对图像的局部区域求取清晰度曲线，在确保成像主体准确聚焦的同时降低计算量。对于成像主体静止且位于画面中心的场合，常见的调焦窗口构建算法包括中心区域法、非均匀采样法、多区域选择法等。

2.1 中心区域法

选择图像中心区域作为调焦窗口是最直接的策略, 如图1(a)所示。其清晰度评价函数为：

(1)

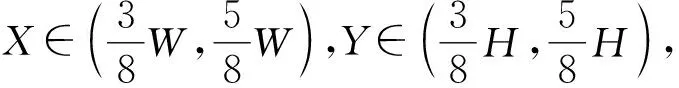
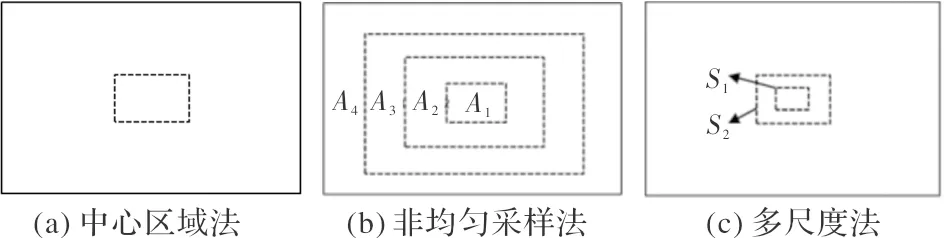
图1 不同调焦窗口示意图

2.2 非均匀采样法

非均匀采样法考虑了背景部分对成像清晰度的影响，以较低的采样率采集图像的边缘部分，以较高的采样率采集中心主体部分，两者共同构成调焦窗口。其调焦窗口如图1(b)所示。采用矩形非均匀采样法的清晰度评价函数为：

(2)

式中：2k-1为采样间隔；k=1,Ak=A1；k=2,Ak=A2-A1；k=3,Ak=A3-A2；k=4,Ak=A4-A3。而且

A4={(X,Y)|X∈(0,W),Y∈(0,H)}。

图2为对一组聚焦程度不同图像序列采用中央区域法、非均匀采样法、多区域法得到的清晰度评价曲线；采用常见的Laplace算子，此时：

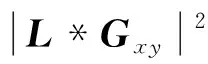
(3)

式中:Gxy为以(x,y)为中心的3×3灰度矩阵;“*”表示二维卷积;L为加权矩阵，可表示为：

(4)

图2 不同调焦窗口的清晰度评价曲线

3 多尺度调焦窗口构建算法

从图2可以看出，上述算法保证了窗口内清晰度曲线与全局图像趋势一致。

以中心区域法为例，考察进一步减小调焦窗口范围得到的清晰度曲线，如图3所示。

可以看出当窗口范围减小为原图的1/8时(指中心区域的边长为原图的1/8)，虽然清晰度曲线出现了多个局部最优点，但峰值点与原图保持一致；当窗口范围减小为原图的1/16时，局部最优点的数量进一步增加，函数峰值已轻微偏离了原图计算的结果；当窗口减小到原图的1/32时，曲线已无法反应出原图清晰度函数的走势。虽然减小窗口可降低计算量，但当窗口范围过小，甚至无法有效覆盖成像主体时，得到的清晰度评价曲线将无法指导聚焦过程。

考虑采用一种分段式调焦算法：第一阶段在清晰度曲线不严重偏离原图趋势的前提下适当减小调焦窗口，以降低求解清晰度值的计算量，相对快速地寻找到局部清晰度函数峰值p1(调焦窗口范围内)；之后增大窗口，保证调整后窗口的清晰度曲线峰值p2与全局聚焦位置一致，当p1临近p2时，从p1出发，第二阶段可以少量步数聚焦。算法流程图如图4所示。

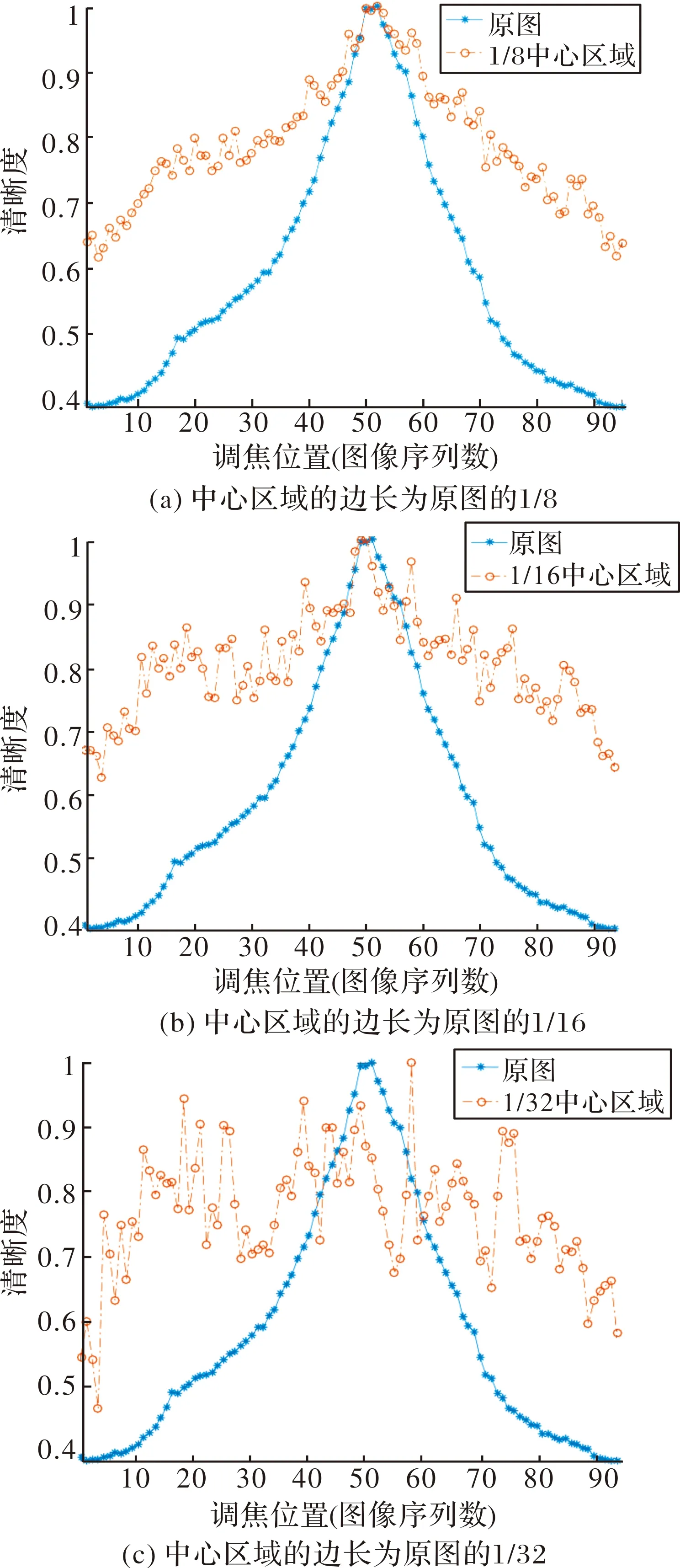
图3 不同尺度窗口清晰度曲线

两个阶段调焦窗口均采用中心区域法，其清晰度评价函数类型如式(1)。为了在清晰度曲线不严重偏离原图趋势的前提下适当减小调焦窗口范围，第一阶段采用原图中心的1/9区域作为调焦窗口；第二阶段为保证调焦窗口清晰度曲线峰值与原图一致，采用原图中心的1/4区域作为调焦窗口。两个阶段调焦窗口如图1(c)所示，表达式为：

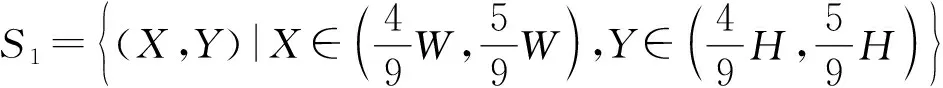
(5)

(6)

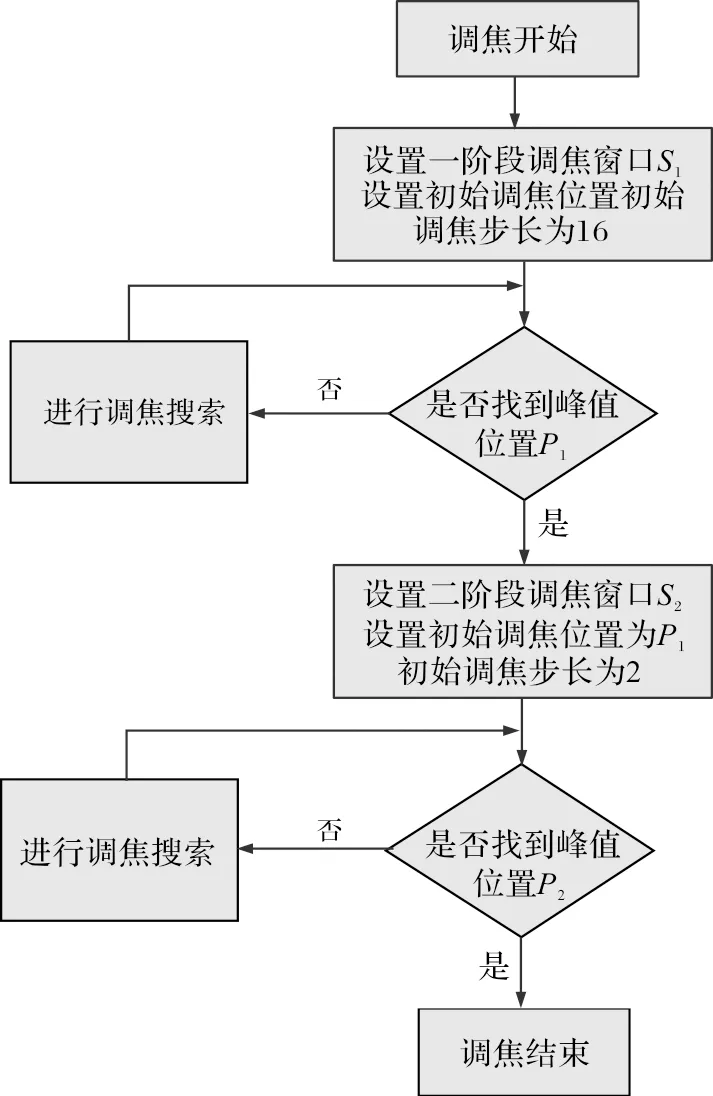
图4 多尺度窗口分段式调焦流程图

调焦采用一种改进的爬山算法[2]。第一阶段调焦时，选择较大初始步长，以避免过早陷入局部最优点；第二阶段调焦时选择较小初始步长，避免在最优点附近过度调整。

4 实验及数据分析

利用某型光学系统采集一组(共95张)离焦程度不同的图像序列(分辨率为768像素×576像素)，相邻序列号图像之间近似认为调焦机构步长为1，选取序列中部分图像如图5所示，完整的清晰度函数如图2所示。

图5 不同离焦程度图像

表1 中心区域法聚焦过程

表2 非均匀采样法聚焦过程

表3 多尺度法一阶段聚焦过程

表1～表4列出了每种调焦窗口的一次典型聚焦过程，其中清晰度取归一化值。由于使用中心区域法和非均匀采样法时清晰度曲线较为平滑，为平衡调焦效率与精度,将初始步长设置为8。对于多尺度法，根据前文所述，第一阶段调焦初始步长设置为16，如表3所示，其中第11步既是第一阶段调焦的终点也是第二阶段的起点；第二阶段初始步长设置为2，如表4所示。每改变一次搜索方向则调焦步长减半，最小步长为1。

表4 多尺度法第二阶段聚焦过程

任意选取10个不同起点进行调焦实验，表5统计了每种算法聚焦的步数。中心区域法、非均匀采样法的平均调焦步数为11；多尺度法第一阶段调焦的平均步数为11，第二阶段平均步数为3。

表5 调焦步数统计

一次典型聚焦过程获取清晰度值所需的计算量θ=λσN，其中λ为平均调焦步数，N为窗口内像素数，σ为单位像素Laplace算子的计算量，对于不同调焦窗口构建算法σ相同。

对于中心区域选择法，N=0.062 5WH(其中W,H为图像的宽和高)，λ=11，θ=0.688σWH；对于非均匀采样法N=0.267WH，λ=11,θ=2.937σWH；对于多尺度法，第一阶段N1=0.012WH，λ1=11,θ1=0.132σWH，第二阶段N2=0.062 5WH，λ2=3,θ2=0.188σWH，θ=θ1+θ2=0.32σWH。可以看出在相同条件下，多尺度法计算量为中心区域选择法的47%，为非均匀采样法的11%，具有更强的实时性。

5 结论

文中提出了一种多尺度调焦窗口构建算法，采用分段式调焦，第一阶段使用小尺寸调焦窗口降低单幅图像清晰度值计算量，相对快速地寻找到局部聚焦位置，之后再适当增大调焦窗口范围，在第二阶段以少量步数准确搜索到全局聚焦位置，实验结果表明该算法可有效提升自动调焦的实时性。