数据驱动的收费站运行参数预测及车道配置

李君羡，周一晨，沈宙彪，张珏蓉，吴志周

数据驱动的收费站运行参数预测及车道配置

李君羡1，周一晨2，沈宙彪3，张珏蓉2，吴志周1

(1. 同济大学 道路与交通工程教育部重点实验室，上海 201804；2. 上海耐特高速公路收费结算有限公司，上海 200063；3. 上海市城市建设设计研究总院(集团)有限公司，上海 200125)

为优化电子不停车收费系统(ETC)推广期间收费站车道配置。依据数据驱动，提出了预测指定日期ETC和人工半自动收费车道(MTC)小时最高流量的方法。结合排队论和驾驶员在收费站选择车道的行为，提出了收费站车道资源配置的优化，并以上海市112个收费站实际数据为例进行验证。研究结果表明：所提出的预测收费站日流量、小时最高流量及ETC流量占比趋势等方法可行，可为收费站车道资源配置提供借鉴。

数据驱动；收费站；车道配置；排队论；电子不停车收费系统

为避免电子不停车收费系统(electronic toll collection，简称为ETC)在推广期间相关设施建设与公众ETC使用增长不匹配的问题，研究供需同时发生变化条件下收费站车道资源配置优化方法尤为必要。Amorim[1]等人以收费站收入最大化为目标，提出收费站建设方案的决策算法，并讨论了ETC收费车道位置对方案的影响。Levinson[2]等人基于社会成本的综合考虑给出了优化ETC车道配置的方案。Tseng[3]等人基于实例，研究了不同ETC/人工半自动收费车道(manual toll collection system，简称为MTC)车道分配条件下，二氧化碳排放量、通行时间及其他外部成本的评估方法。周崇华[4]等人基于排队理论和增量效益成本比率，建立 ETC车道优化配置模型。曲明革[5]以济南南收费站数据验证M/G/K排队模型有效性，考虑断面交通量、收费站平均服务时间和收费站服务水平，计算多个因素组合下的收费站通行能力，但仅考虑了MTC模式。廖固[6]讨论了不同ETC需求和供给情况下收费站的通行能力。基于M/M/n排队模型，姬扬蓓蓓[7]等人在收费站车道总量一定、流量不同、ETC占比不同条件下，以成本为约束，针对特定收费站计算了ETC/MTC收费车道比例配置最优解。郭英明[8]等人基于车辆总损失的概念，给出了收费车道资源配置优化算法。吴进[9]通过仿真输出流量、ETC缴费比例及ETC车道数不同组合条件下的延误，基于通行效用比，选ETC车道设置方案。何石坚[10]等人同样以仿真为手段，证明应随到达流量和ETC流量比动态调整车道配置方案。

目前，在短期内大力推广ETC收费具有强制性，与以往研究的基础假设存在较大差异。为避免模型复杂、仿真模型可靠性有限等问题，本研究基于真实数据的供需、变化条件下的流量预测及驾驶员车道选择行为，拟以不同类型过车服务供需匹配、收费站服务稳定性为主要约束，提出收费站车道配置优化方法。

1 数据及方法概述

1.1 数据及预处理

收集的数据有：①上海112个收费站所有车道的编号、方向及收费模式；②收费车道2019年6月—9月逐日流量数据；③第一组数据为上海G2安亭、G2江桥及G60新桥主线3个收费站(称为1～3号收费站)2019年8月12日至25日14 d入口/出口流量、每小时流量及ETC/MTC流量。

将①,②数据表根据车道编号做内连接，整理得到2019年6月−9月所有收费站分车道逐日流量数据，附上所在收费站、收费模式及入/出方向标记属性，称为第二组数据。

随着ETC服务推广，以ETC方式缴费的客车数量逐渐增加。由于上海市未对货运车辆安装ETC做强制要求，故95%以上货运车辆仍以MTC方式通行。设施方面，完成改建的ETC车道仅允许ETC车辆通行，MTC车道则允许两类车辆混行，但MTC车道一般设置在收费站两侧，已安装ETC缴费设备的车辆几乎不经过MTC车道通行。因此，可近似认为ETC、MTC车道服务类型为单一方式，同一车道不存在2种缴费模式混合情况。这一条件随着ETC的推广会根据实际数据进行修正。

1.2 方法流程

考虑目前收费站通行供需匹配及服务指标，提出收费站资源配置优化方法，流程如图1所示。

2 收费站交通流特征参数分析与预测

2.1 收费站日流量预测

2.1.1 基于流量周期可重现性的预测方法

基于历史数据规律，预测收费站日流量计算代价最小，所以优先考虑。考察流量周期可重现性，借鉴向量间相似性系数[11]，构造最大归一化相似性系数为：

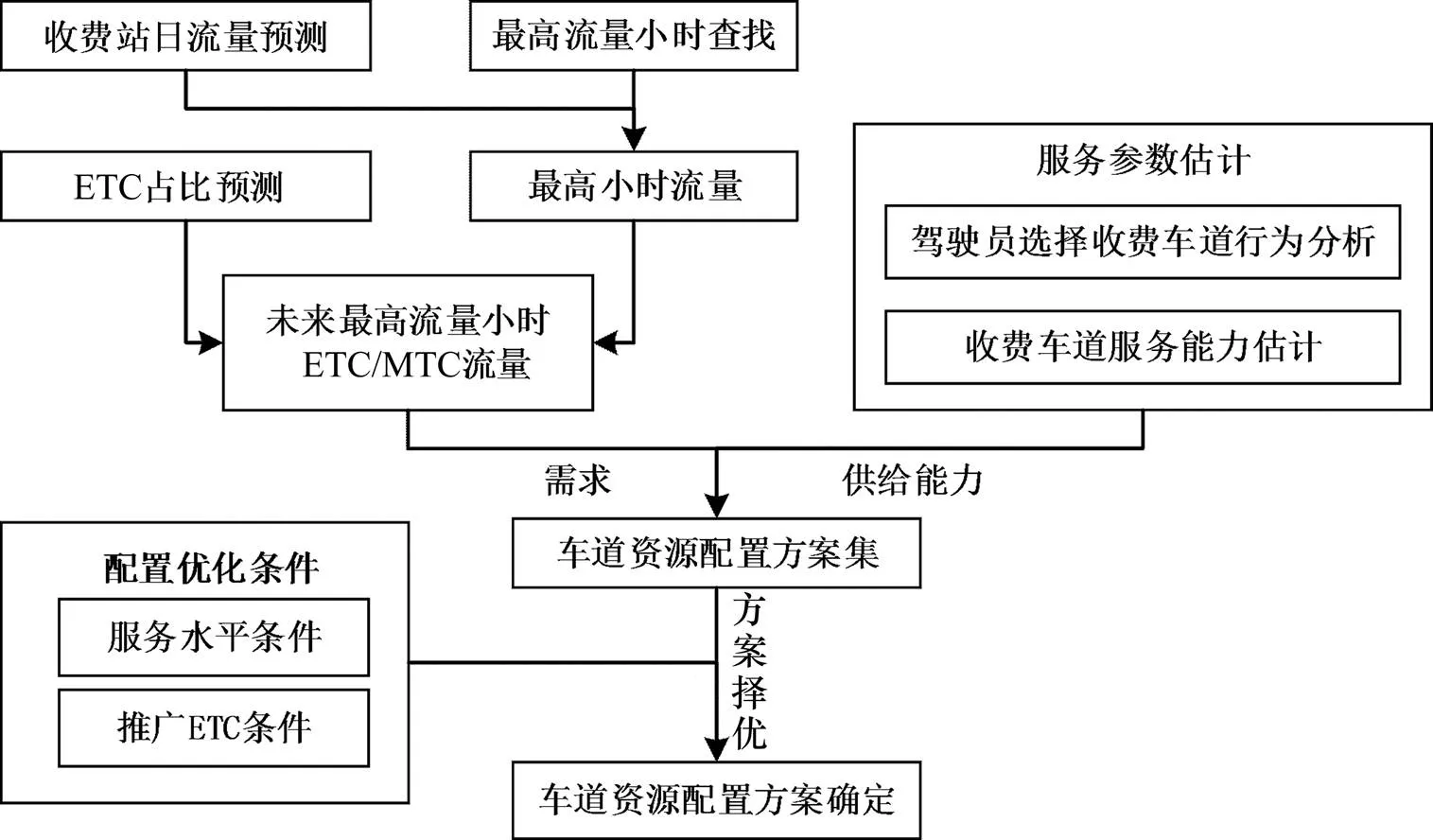
图1 方法流程

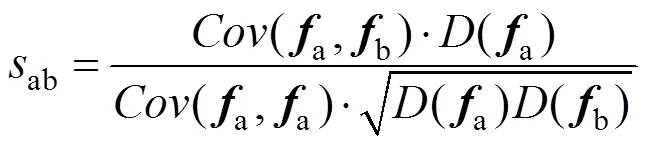
本研究中，向量为指定收费站入口/出口7 d的日流量构成的序列。以3号收费站为例，7 d为一周期，研究第二组数据6—8月(覆盖13个完整周期)每日入口流量可重现性，计算该周期两两之间最大归一化相似性系数，绘制热力图如图2所示。从图2中可以看出，3号收费站各周期流量变化不稳定，工作日和周末可重现性均较差。

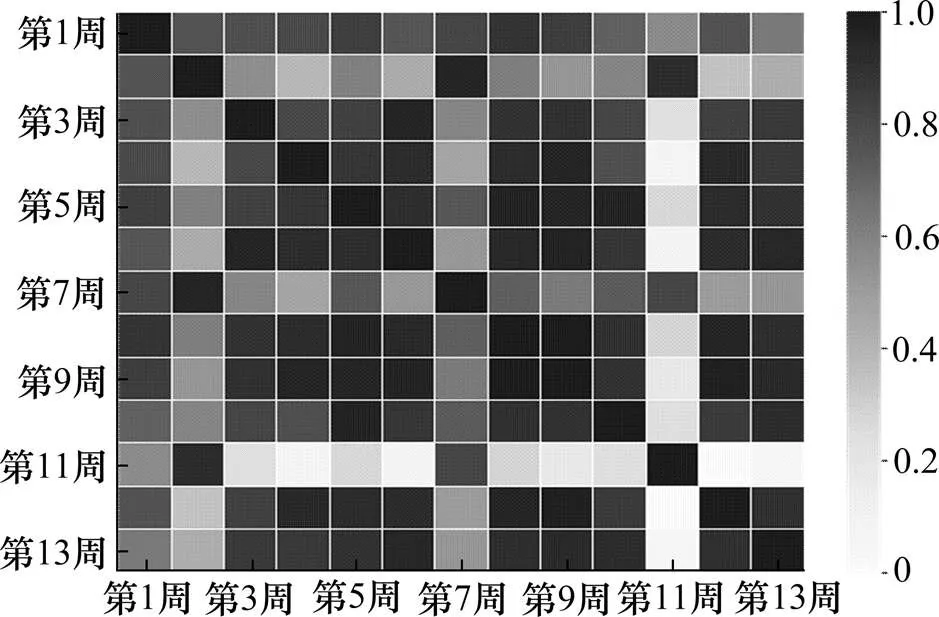
图2 3号收费站周期间最大归一化相似性系数热力

同样的方法对其他111个收费站进行操作，流量周期可重现性统计见表1。由表1可知本方法对于多数收费站实用性较差，作为流量预测的方法不够理想。

2.1.2 基于时间序列分析的预测方法

以3号收费站为例，将该站6—8月日入口流量整理为连续92 d的流量−时间序列作为训练样本，并提取其9月数据为测试样本。

表1 收费站流量周期可重现性统计

对训练样本进行ADF平稳性检验[12]，各项指标见表2第二列。统计值在1%置信度下未通过检验，而值较大，即该曲线不平稳。对其一阶差分后再次检验指标见表2第三列，指标显示其为平稳数列，可用于进一步分析。

表2 3号收费站流量时间序列平稳检验指标值

绘制训练样本一阶差分数列的自相关图和偏自相关图。根据图像预选、值组合建立多个ARMA模型试算。采用统计量检验[12]对残差进行白噪声检验。基于AIC准则，选择最佳模型参数并训练，预选出3组模型参数均通过白噪声检验，模型参数与评价指标见表3。

表3 3号收费站ARIMA模型试算表

选择表现最佳的疏系数模型ARMA(4,4)对一阶差分序列滚动预测，得到3号收费站9月每日入口流量预测值与真实值对比，如图3所示。

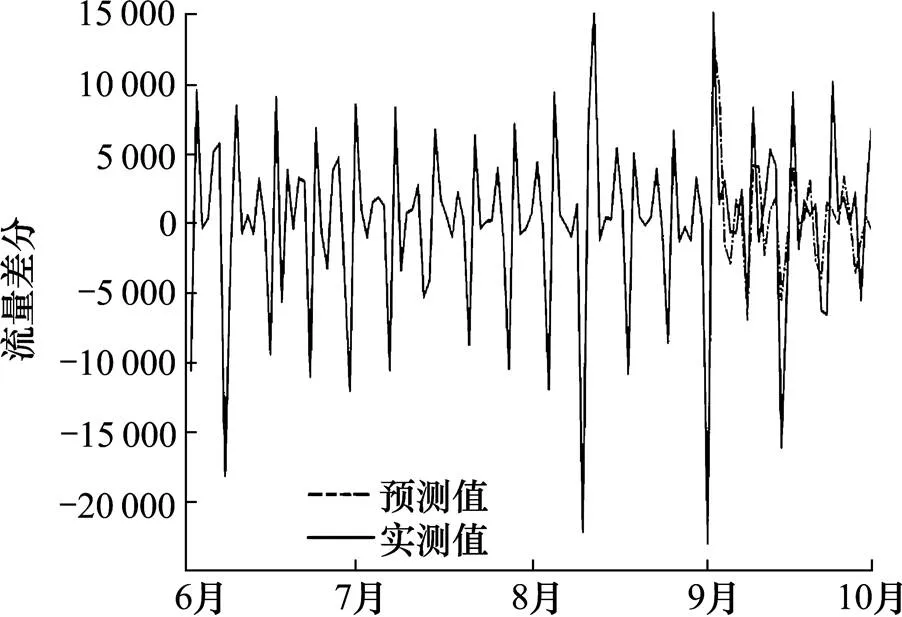
图3 优选模型预测值与真实值对比

采用6—8月数据，基于流量周期可重现性方法，取周期内对应日期历史均值，对3号收费站9月日入口流量进行预测，日均误差为5.74%，单日最高误差达31.35%。而基于时间序列分析的预测方法，得到日均误差为3.64%，最高误差为19.02%，可见基于时间序列预测的优势。

随机选取其他50个收费站6−9月入/出口日流量时间序列，共100个数列。用基于时间序列的方法搜索建模并择优，发现原序列一阶差分后均为平稳数列。可尝试以基于时间序列分析的方法进行流量预测，但模型的类型及相应关键参数均存在较大差异，统计情况见表4。

表4 时间序列分析方法流量预测建模类型统计

使用基于时间序列分析预测收费站流量可行，对不同收费站的入口/出口流量预测需分别建模，并寻优定参，进而开展后续工作。建议采用滚动预测，考虑数据逐日更新1条，每日合并数据，重新拟合。运算量较大，可基于新观测值微调原拟合模型或定期更新模型。

2.2 最高流量小时查找

收费车道数量计算依据标准设计小时交通量，而收费站流量在1 d各小时分布不均匀，所以需基于预测日流量，进一步查找全天流量最大小时(以下简称高峰小时)，获取流量特征，便于后续配置优化中以该小时服务水平为约束，进行极限分析。

仍优先考虑基于日流量曲线相似性查找高峰小时。以3号收费站为例，取第一组数据14 d入口流量数据，以24 h为周期考察流量−小时曲线，计算最大归一化相似性系数，并绘制热力图如图4所示，工作日流量分布高度一致。周末与工作日相似性略低，且周末2天也有一定差异。1,2号收费站结果类似，日流量曲线可复现性较好，可作为最高流量小时查找依据。具体时间在实际计算时，应考虑各收费站特性差异，分别分析。

2.3 ETC日占比增长预测

得到高峰小时流量后，进一步将收费站过车按照缴费模式分别统计流量，可转化为求取ETC日占比问题。ETC推广期间，各收费站ETC缴费车辆不断增加，需预测ETC流量占比。综合第二组数据中多个收费站入/出口ETC占比趋势(其中，2,3号收费站日入口流量ETC占比趋势如图5所示)，剔除异常点。结果表明：各收费站ETC占比均呈上升趋势，该趋势周期性波动，但振幅不断减小。受不同收费站区位、外地车比例、进出方向影响，其上升阶段与增长速度不一致。

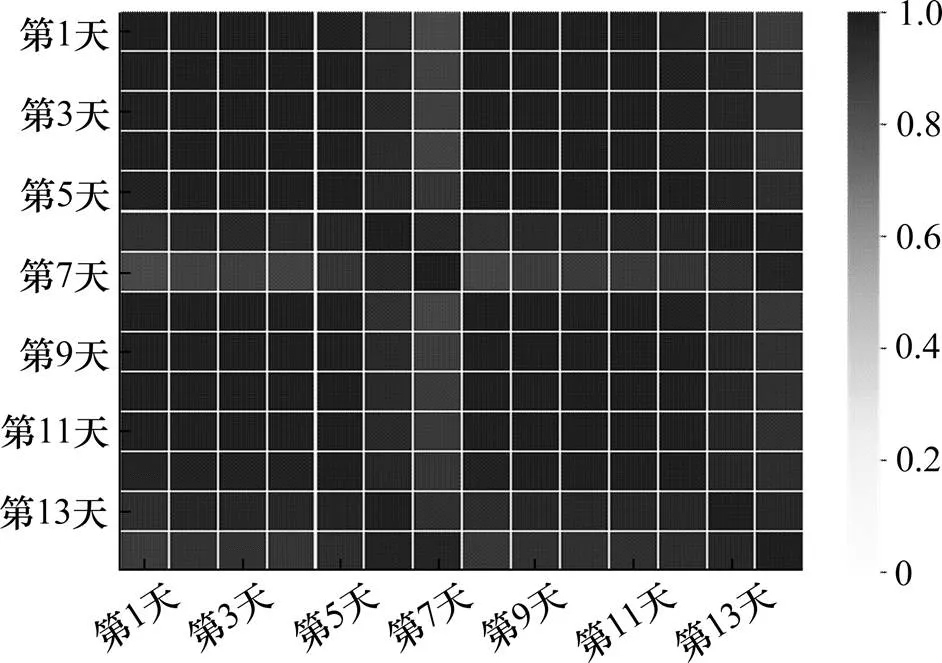
图4 3号收费站两周流量−小时数据归一化相似性系数热力图

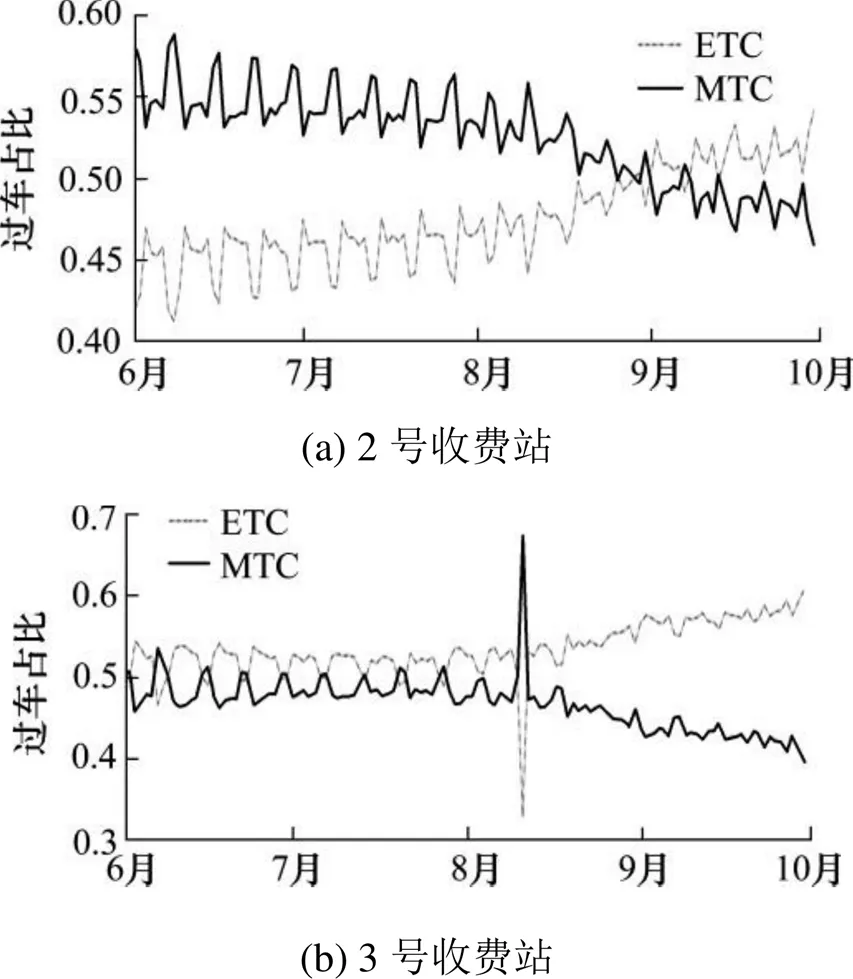
图5 2,3号收费站入口ETC/MTC流量占比曲线

ETC占比呈周期性，可以用时间序列模型进行预测，但过程较复杂。考虑其波动性极差且逐渐减小，至9月末已降低至0.025，故忽略波动性，以多项式近似拟合趋势。以3号收费站为例，分别以线性、二次多项式、三次多项式对其6—8月ETC占比增长趋势，拟合曲线指数系数2分别为0.446 8、0.479 3、0.501 3。为避免过拟合，分别以3个模型预测9月份数据，并与前3个月的数据合并进行总体误差检验，线性三次多项式拟合2分别为0.636 5、0.7705、0.383 5，线性二次多项式6—9月趋势拟合曲线如图6所示。

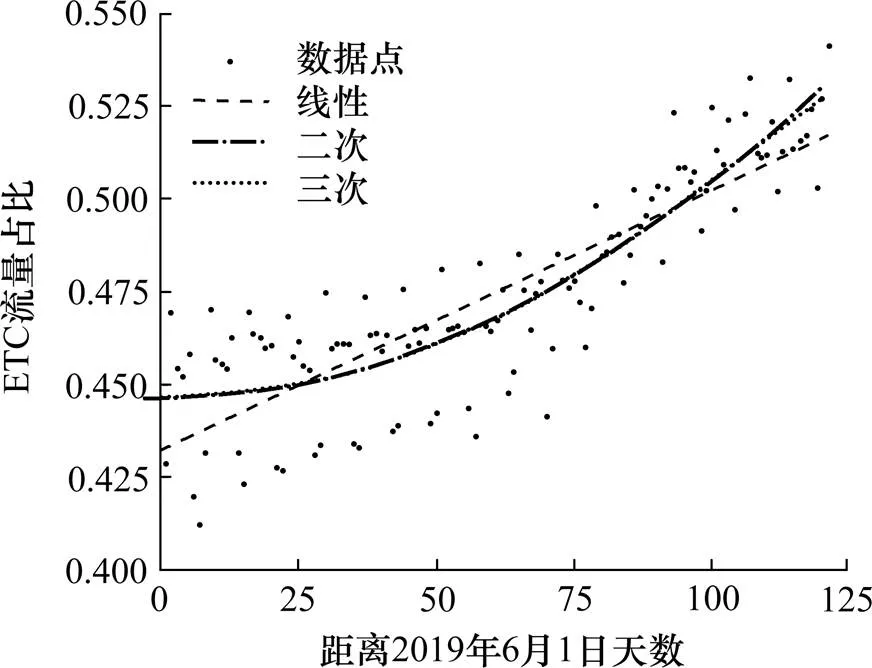
图6 3号收费站入口ETC流量占比拟合分析

随着ETC全面推广，二次多项式效果不断增强，其余若干收费站测试结果表明：ETC增长，均可用二次或三次多项式以较高精度拟合。

统一采用当日ETC占比，也可进一步考察各小时ETC占比，针对最高流量小时专门研究。在实际应用时，为同时保留ETC日增长趋势信息和小时波动信息，可在ETC日增长曲线的基础上，考虑高峰小时的比例对日均值比的变化，对该小时ETC占比参数进行修正。

3 收费站服务特征参数分析与标定

3.1 驾驶员选择收费车道行为分析

取第二组数据6—9月共122 d 3个收费站入/出口分车道收费数据，只保留全天所有小时开放收费车道一致的记录(筛选后，各收费站记录数均保持在115条以上)，避免偶尔开放的车道干扰分析，以横轴为车道编号(与车道位置无关)，对比ETC、MTC各收费车道与当日同类流量最大车道的流量比例及多日比例均值，如图7,8所示。

不论入/出口，车辆并非随机选择缴费车道。多个收费车道同时开放且未达到饱和状态时，驾驶员不一定选择最短排队的车道，而是愿意忍受一定的排队，选择最容易进入的车道避免交织。此行为导致该主线正对的收费车道服务强度大于其他的，呈现逐渐向两侧递减并稳定的比例规律。当优选车道排队超过忍受限度，若邻近车道排队更短，驾驶员会转向邻近车道。因此，流量较大时，各车道流量分配也趋于均匀化。ETC和MTC模式驾驶员可忍受的排队长度不同，同一收费模式驾驶员对不同位置车道可忍受的排队长度也不同。其中，优选车道可忍受的排队长度最长。为便于计算，以平均忍受长度作为计算参数。

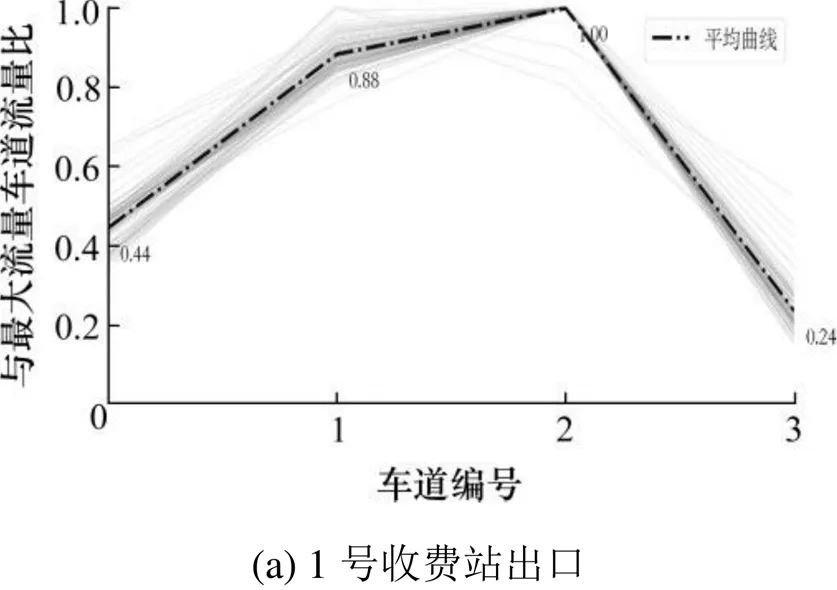
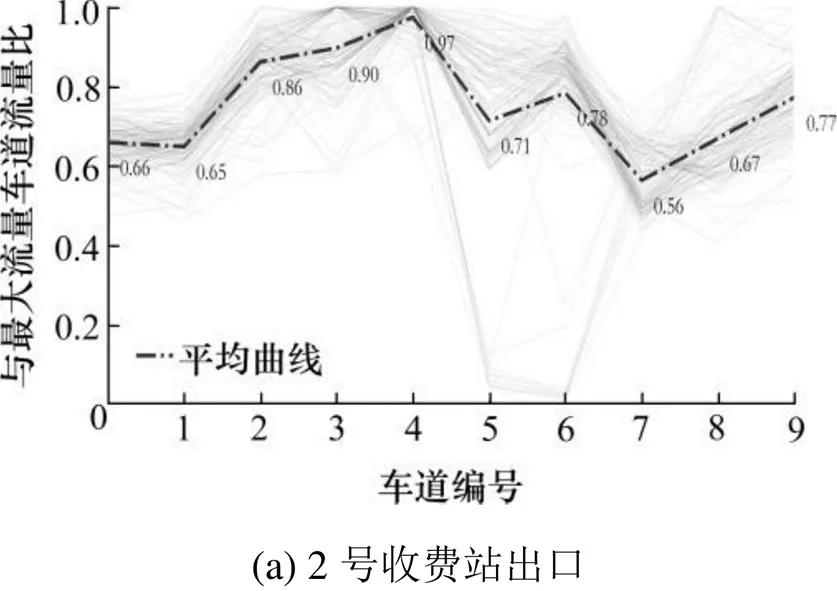
选择图7,8中车道流量分配均匀的收费站数据，认为最大流量车道排队已达驾驶员容忍限度。结合收费站各车道流量，求解ETC/MTC模式驾驶员可忍受排队长度。排队忍受长度为驾驶员主观感受，故同时以车辆数及pcu为单位[13]给出结论见表5，数值向下取整。

表5 不同类型车道驾驶员可忍受排队长度

由表5可知，可见ETC车道驾驶员排队耐受性更小，推测与ETC用户对通行效率要求更高有关。数据显示出口处ETC有1个排队车辆时，会发生驾驶员就近排队转移行为，这与数据收集期间ETC车道开放远超实际需求，大多数ETC车道远未达到服务饱和状态有关，计算结果偏低。此外，研究期间上海ETC车道基本无货运车辆通过，随着未来面向货运车辆推广ETC，相应忍受排队车辆数也将有所增加，则持续观测车道选择行为将进行更新。

3.2 收费车道通行能力估计

本研究数据最小颗粒度为小时，无法基于实测数据直接获得各类收费车道的通行能力。但在收费站服务强度较大时，与主线正对车道服务能力趋于饱和。因此，选择高饱和小时，查找最高流量车道，以其流量求得饱和服务时长，过程中将各类过车类型折合为标准小汽车当量[13]统一计算。则：

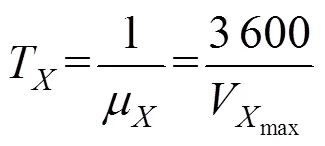
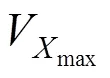
求解3个收费站入口/出口ETC/MTC的平均服务时间见表6(1号收费站入口无ETC)。

表6 收费站两类车道平均服务时间

各收费站大型车占比和土建设计方案等存在差异，故各收费站的服务时间不同。在实际运算中，应分别处理。若缺乏数据，可认为MTC入口、出口服务时间约为4.9 s和14.5 s；ETC入口、出口服务时间约为3.4 s和3.6 s。

4 收费车道配置方案的优化

4.1 基于推广ETC考虑的配置优化

为推进ETC普及工作，保持现有收费站车道总数不增加，通过调整ETC、MTC车道的比例，保证ETC车道排队长度不大于MTC车道。

根据假设模型，考虑已标定的参数，该约束可表示为：

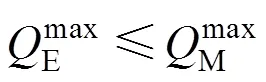
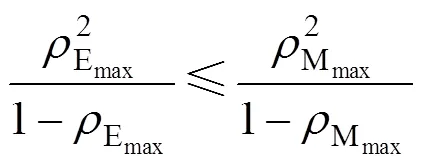
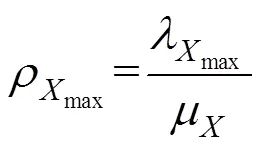
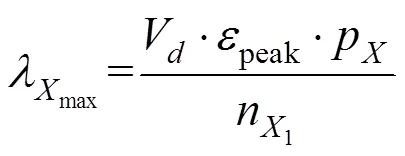
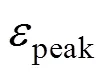
有车道总数约束式：

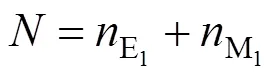
其中，为该方向总收费车道数。将(5)～(7)代入式(4)，则有：

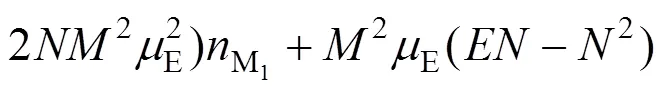
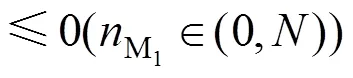
4.2 基于服务水平的配置优化

基于ETC推广考虑的配置方案只满足了ETC和MTC车道的相对关系，未约束两者数量的最低值，最低值受收费站服务水平限制。

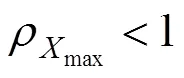
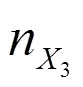
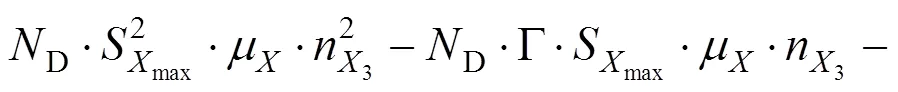
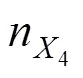
一般条件三的约束力最强，可根据不同流量的条件及适用情况进行选择，并计算。

5 计算实例

抽取3号收费站9月15、16日2 d入口/出口运行情况作为实例，该收费站入、出口分别开放9条、18条收费车道。假设ETC/MTC车道各有一条车道正对主线，其余车道依次向两侧分布。以排队超过8 pcu作为阻塞主线条件，综合各模型，求得的参数见表7。

由表7可知，3个月服务水平约束下，有多组可行解，需配合最大排队相等条件优化，进一步参照表5排队忍受值选择稳定解。以9月16日出口流量为例，除表中E6M12方案最优解外，还有E10M8组合。此时ETC、MTC车道平均排队为1 pcu和6 pcu，后者未达到拥堵水平，但其排队长度在折算后，接近出口MTC车道排队车辆数容忍值，驾驶员可能向就近车道转移，可视为不稳定状态。调整为E9M9组合，重新计算，此时ETC、MTC车道排队长度为1 pcu和3 pcu，满足排队忍受值且无车道转移，为稳定解，可作备选方案。

表7 实例计算结果

注：EM表示ETC车道配置条件，MTC车道配置条。

6 结论

在目前收费站ETC推广条件下，探究了车道资源配置的优化方法，得到的结论为：

1) 基于实际数据，提出了收费站流量、最高流量小时及流量比、ETC车辆占比等预测方法，结果证明基于时间序列、周期可复现性和多项式拟合为预测这些关键参数的可行方法，具有较好效果。

2) 对收费站服务特征参数，如：驾驶员排队特征、收费站服务时间等参数，提出估计方法，并给出统计性结论，作为收费站资源配置参数参考。

3) 结合预测和统计结果，考虑ETC其他服务条件约束，提出收费站车道资源配置优化计算方法，实例证明方法可行。该方法可供2种收费模式并存、ETC服务供需同时变化场景下的收费站资源配置设计进行借鉴。

除了基于服务水平指标外，在考虑收费站车道资源配置方案时，尚需考虑运营成本、时间延误成本及环境能源成本等诸多因素，在后续工作中可在结论基础上做进一步研究。

[1] Amorim M, Lobo A, Rodrigues C, et al. Optimal location of electronic toll gantries: The case of a Portuguese freeway[J]. Procedia Social and Behavioral Sciences, 2014, 111: 880−889.

[2] Levinson D, Chang E. A model for optimizing electronic toll collection systems[J]. Transportation Research Part A: Policy and Practice,2003,37(4):293−314.

[3] Tseng P H,Lin D Y,Chien S.Investigating the impact of highway electronic toll collection to the external cost: A case study in Taiwan[J].Technological Forecasting and Social Change,2014,86:265−272.

[4] 周崇华,周九州,苏志哲.基于排队论和增量效益成本比率最大化的ETC车道配置模型研究[J].交通运输系统工程与信息, 2009, 9(5): 77−84. (ZHOU Chong-hua, ZHOU Jiu-zhou, SU Zhi-zhe. Modeling ETC lane deployment based on queuing theory and incremental- benefit-cost ratio maximum[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(5):77−84.(in Chinese))

[5] 曲明革.高速公路出入口收费车道数研究[J].公路,2012, 57(5):262−267.(QU Ming-ge. Research on the toll lane count of the entrances and exits of highway[J].Highway, 2012,57(5):262−267.(in Chinese))

[6] 廖固.高速公路收费站通行能力分析[J].公路工程,2010, 35(3):153−155,172.(LIAO Gu.Analysis of expressway tollgate capacity[J]. Highway Engineering, 2010, 35(3): 153−155,172.(in Chinese))

[7] 姬杨蓓蓓,周金凤.基于成本分析的高速公路收费站车道配置研究[J].重庆交通大学学报:自然科学版,2018, 37(1):85−91. (JI Yangbeibei, ZHOU Jin-feng. Lane allocation of highway toll gate based on cost analysis[J]. Journal of Chongqing Jiaotong University: Natural Science,2018,37(1):85−91.(in Chinese))

[8] 郭英明.基于车道排队系统模型的高速公路收费站资源配置优化研究[J].价值工程,2015,34(11):198−201.(GUO Ying-ming. Optimization of expressway toll-gate resource allocation based on lane queuing system model [J].Value Engineering,2015,34(11):198−201.(in Chinese))

[9] 吴进.基于通行效用的高速公路收费站ETC车道设置方案研究[D].南京:东南大学,2016.(WU Jin. The research on etc lane setting scheme of highway toll station based on the traffic utility[D]. Nanjing: Southeast University,2016. (in Chinese))

[10] 何石坚,李清波,匡姣姣,等.高速公路混合收费站通行能力的仿真[J].交通科学与工程,2015,31(3):106−111.(HE Shi-jian, LI Qing-bo, KUANG Jiao-jiao, et al. Simulation of the traffic capacity of the composite toll station in highway[J].Journal of Transport Science and Engineering, 2015,31(3):106−111.(in Chinese))

[11] 段征宇.基于动态交通信息的车辆路径优化[M].上海: 同济大学出版社,2015.(DUAN Zheng-yu.Vehicle routing optimization based on the dynamic traffic information[M]. Shanghai: Tongji University Press,2015.(in Chinese))

[12] 周永道,王会琦,吕王勇.时间序列分析及应用[M].北京: 高等教育出版社,2015.(ZHOU Yong-dao, WANG Hui-qi, LYU Wang-yong. Time series analysis and its application [M].Beijing: Higher Education Press, 2015.(in Chinese))

[13] 中华人民共和国交通运输部.公路工程技术标准 JTG B01—2014[S].北京:人民交通出版社,2015.(Technical standard of highway engineering.JTG B01—2014[S]. Beijing:China Communications Press,2015.(in Chinese))

Operation parameter prediction and lane allocation optimization of toll station driven by data

LI Jun-xian1, ZHOU Yi-chen2, SHEN Zhou-biao3, ZHANG Jue-rong2, WU Zhi-zhou1

(1. Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China; 2. Shanghai Naite Expressway Toll Settlement Co., Ltd., Shanghai 200063, China; 3.Shanghai Urban Construction Design and Research Institute (Group) Co., Ltd., Shanghai 200125, China)

To study lane allocation optimization during the ETC promotion period, a data-driven method was presented to predict ETC and MTC volumes in the peak hour of a coming day. Combined with queue theory and drivers’ behavior of choosing toll lanes, a method was proposed to optimize the lane allocation scheme. Actual operation data of 112 toll stations in Shanghai were collected to illustrate the manipulation. The outcome suggests that methods proposed are applicable to predict the daily flow of toll stations, the highest-volume hour of toll station, and the growing trend of ETC traffic, which could contribute to decide the lane allocation scheme.

data-driven; toll station; lane allocation; queuing theory; ETC

U491.4

A

1674 − 599X(2021)01 − 0095 − 09

2020−07−20

国家自然科学基金项目资助(61773288)

李君羡(1987−)，女，同济大学博士生。