循环荷载作用下铁路道床的离散元分析

张帅辉，周陶勇，许平，张亚晴，夏建军

循环荷载作用下铁路道床的离散元分析

张帅辉，周陶勇，许平，张亚晴，夏建军

(昆明理工大学 机电工程学院，云南 昆明 650500)

为研究高速有砟道床中存在的累积沉降变化规律，通过PFC离散元软件，建立一定级配的高速铁路散粒体有砟道床的三维离散元模型。选取循环荷载频率分别为5,10,20,30 Hz，荷载幅值为3,5 kN，共8种荷载工况进行数值模拟，分析了道床力学性能，探讨了循环荷载的频率和振幅对道床沉降的影响。研究结果表明：循环荷载频率不超过20 Hz时，荷载频率对道床的沉降量及沉降速率的影响较小；循环荷载频率30 Hz时，其对道床的沉降量及沉降速率的影响显著增大；循环荷载幅值越大，道床的沉降量、沉降速率越大；循环荷载频率越大，道床的垂向刚度越大。

铁路道砟；循环荷载；离散元法；道床沉降

随着科学技术的不断发展，铁路逐步向高速化、重载化方向发展，考虑到成本和地况等方面的原因，部分铁路线路不可避免的使用有砟轨道结构[1]。针对有砟轨道在高速循环动载荷作用下出现的沉降变形，须开展相关的研究。Tutumluer[2]等人通过建立有砟道床离散元模型，研究荷载重复作用下道床的累积变形。Al-Saoudi[3]等人基于道砟箱的道砟集料累积变形试验，得出荷载幅值越大，道砟集料的累积变形也越大。姜卫利[4]等人建立了有砟道床二维单元模型，研究道床在不同荷载下的应力变化。张徐[5]等人采用PFC研究道砟的破碎机理。通过将国内外对散粒体道床的研究作对比，发现中国在该领域的研究还有所欠缺。在列车行驶过程中，由于高速循环动载荷作用，有砟轨道的荷载频率和荷载幅值不断增大，使道床的不均匀沉降速率也相应加快，从而改变有砟道床的力学性能，影响列车运行的安全性，乘客的舒适度等。为了进一步探究高速有砟道床中存在的动态劣化现象，作者拟采用离散元法研究散粒体道床在列车循环荷载作用下的累积沉降规律。

1 离散元简介

20世纪70年代，Cundall[6−7]等人提出了离散元方法(digital elevation model, 简称为DEM)。最初是用于建立岩体二维模型，分析其边坡的稳定性。现在用该数值模拟方法解决不连续介质问题，广泛应用于岩土工程、土力学等领域。岩体是无规则的几何体，具有散体的特性。在力的作用下，岩体内部发生旋转、滑动，从外观表现为岩块的破碎等。为了更形象的研究岩体内部的变化，利用离散元法将其内部以圆球颗粒填充，分析颗粒间的相互作用，模拟整体的受力和变形。

本研究利用PFC离散元软件模拟有砟道床颗粒间的相互作用，分析材料的受力及变形。在PFC软件中，有2种颗粒间的接触，一种是球—球接触，另一种为球—墙接触。当接触间隙c为0(无张力和摩擦)时，表明颗粒处在接触状态，如图1所示。

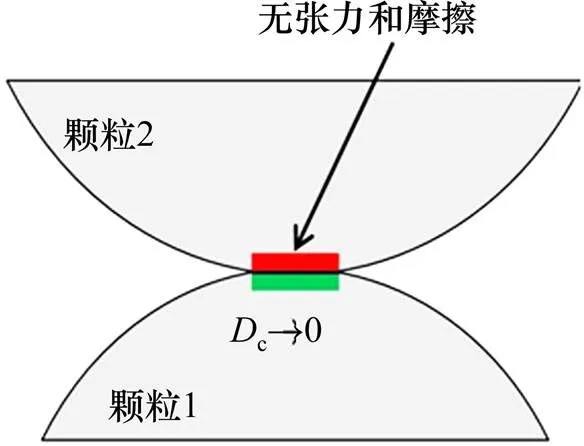
图1 颗粒间接触说明

2 建立模型

2.1 建立道砟颗粒模型

道砟作为有砟铁路的重要组成部分之一，能为轨枕提供弹性、吸收能量、减少噪声及列车振动，同时还具有吸热、增加透水性等作用。道砟颗粒是一种无规则的几何体，具有散体的特性。在建立道砟颗粒模型时，可以采用单个球模拟道砟，也可以采用若干个球组合模拟道砟，还可以通过图像识别的办法重建道砟。本研究采用图像识别的方法获取道砟颗粒的三维几何模型，能更精确地获得道砟的几何边界，使道砟模型更逼真。再将道砟颗粒模型导入PFC软件，进行颗粒填充和道床创建。然后建立不同级配与不同密实度的道床模型。

2.2 数字高程模型

1) 获取道砟颗粒图像

固定道砟颗粒，在同一水平面上，利用相机对道砟颗粒环绕一周拍摄，如图2(a)所示，图片越多，效果越好。

2) 提取道砟点云图像

将拍摄的道砟颗粒图片导入到VisualSFM中进行特征提取，得到点云图像，如图2(b)所示。然后将点云图像导入到Meshlab中进行创建纹理图像，如图2(c)所示。创建出的道砟模型在外观上可以看出与真实道砟颗粒一致，但大部分会得到不完全封闭的颗粒模型，需要在Netfabb将道砟颗粒模型进行封闭如图2(d)所示，以便进行后续的建模。

3) 获取道砟颗粒簇模型

将封闭的道砟颗粒模型导入PFC中，采用不同半径的球形单元，使用多球叠加的方式进行填充，如图2(e)所示。

2.3 建立有砟道床模型

道砟颗粒组成的道床会因不同级配呈现不同的力学特性。因此，选用道砟颗粒时，应按照一定级配标准进行选取[8−9]。中国针对高速有砟铁路道砟颗粒的选择应按照特级道砟级配设计进行选取，即采用粒径分布相对集中的道砟颗粒，其方孔筛边长为31.5～50 mm、颗粒质量百分率≥50%进行级配设计。

通过本试验的道砟颗粒建模方式，按照一定级配标准选取道砟颗粒，并将其填充到道床中。其中，道床模型长度为60 cm，宽度为30 cm，按照高速铁路设计规范，厚度设为35 cm，道床初始孔隙率设置为0.55，轨枕底面宽度为30 cm，道砟颗粒间的接触为线性接触，且满足Coulomb摩擦定律。在实际研究过程中，可参照式(1)，式(2)对道床材料的模型参数进行设置：

图2 道砟颗粒模型

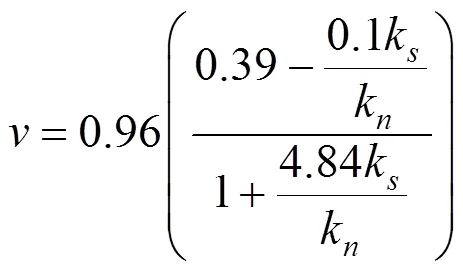
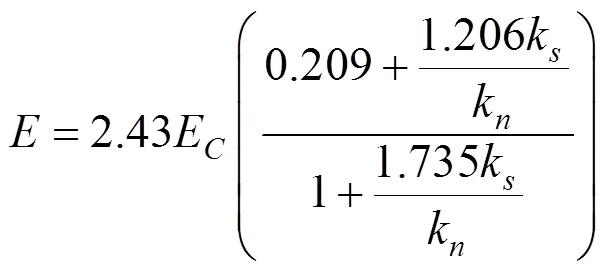
式中：为材料的泊松比；k/k为切向法向刚度比；为宏观杨氏模量，N/m2；E为颗粒间接触弹性模量，MPa。

根据学者研究有砟道床时使用的参数进行设置，然后经过多次调整，得到道砟颗粒和墙体侧面边界的法向接触刚度均为1.5×108N/m，道砟颗粒和墙体底面边界的切向接触刚度均为1.0×108N/m，道砟颗粒的接触摩擦系数为0.5，道砟颗粒与墙体间的摩擦系数为0.6，道砟颗粒的密度为2 810kg/m3,轨枕密度为2 400kg/m3，道砟颗粒的阻尼系数为0.15。

在PFC软件中将模型进行初始化。由于生成的道床模型中颗粒位置杂乱无章或颗粒重叠，属于非平衡状态。为使模拟效果更真实，需要对道床模型进行初始化，在PFC中体现为伺服控制，即改变道砟颗粒间、颗粒与墙体间的接触关系。通过对道砟颗粒体系施压，使道砟颗粒间、颗粒与墙体间紧密接触，让道床模型接近真实状态，如图3所示。

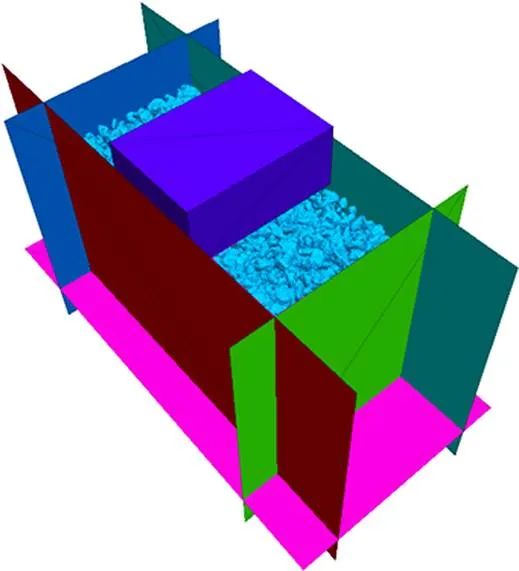
图3 有砟道床模型

在轨枕的质心处施加循环简谐荷载，也就是在轨枕的质心处垂直施加正弦力进行仿真分析。在实际工况下，有砟道床的轨枕长为250 cm，钢轨支点的平均压力为24.4～46.3 kN。假设轨枕底部受力均匀，则30 cm长的轨枕模型的受力为2.9～5.5 kN。

3 有砟道床的仿真分析

为研究循环荷载频率与荷载幅值对道床沉降的影响。在仿真过程中，由于轨枕始终接触道砟颗粒，不发生悬空现象，因此，选取轨枕的沉降量作为有砟道床总体的沉降量[10−14]。在一定荷载频率和荷载幅值状态下，轨枕垂向位移的仿真模拟结果如图4所示。

从图4中可以看出，道床在一次加载卸载过程，加载时有垂向位移，卸载时有回弹，但无法恢复至原始位置，表明有残余变形的存在。随着循环次数的增加，道床残余累积变形逐渐增大。

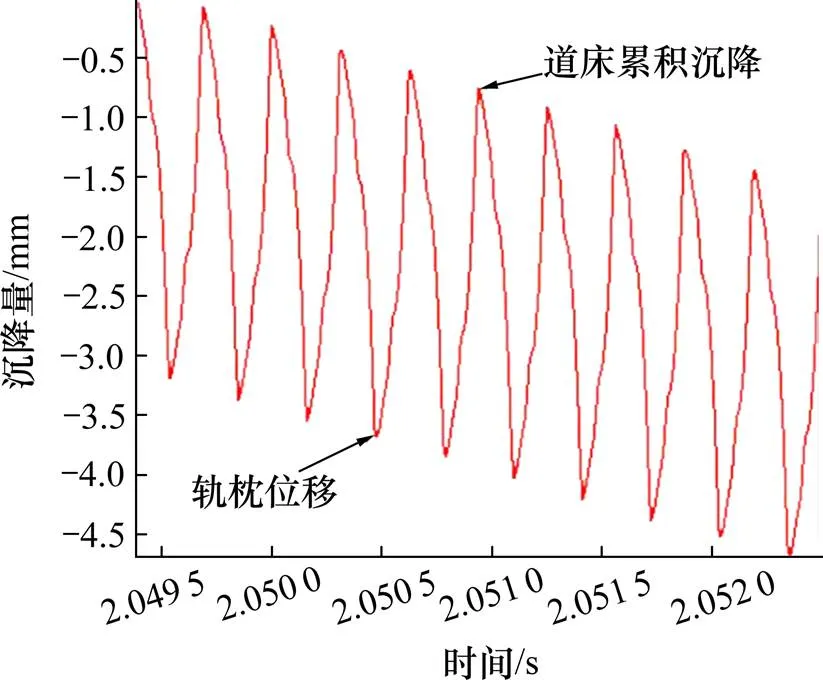
图4 道床累计变形

3.1 循环荷载的频率和幅值对道床沉降影响

选取荷载频率分别为5,10,20,30 Hz，荷载幅值分别为3,5 kN，共8种荷载工况进行模拟试验。在PFC软件中，模拟实际时间1 s至少需要循环十万次以上，通过观察仿真数据，在模拟循环荷载加载次数为150次后，道床的累计沉降量变化不大。4种循环荷载频率和2种荷载幅值状况下有砟道床的离散元模拟结果如图5所示。

从图5中可以看出，仿真过程中循环荷载次数增加；在8种工况中，道床的沉降变形为线性增大。3 kN荷载幅值下5,10,20 Hz荷载频率时的道床沉降变形较小，且趋势基本重合，沉降量均为0.04 mm左右；5 kN荷载幅值下，5,10 Hz荷载频率时的道床沉降变形趋势基本重合，沉降量均为0.08 mm左右。不同荷载幅值下，30 Hz荷载频率时的道床沉降变形较大，趋势最为明显。所以在荷载频率为30 Hz与荷载幅值为5 kN时，道床沉降量最大。表明：循环荷载的频率和幅值越高，道床沉降变形越显著。

3.2 循环荷载的频率和幅值对道床沉降速率影响

在不同工况下，将道床的沉降变形量拟合成线性模型，取线性模型中直线的斜率作为道床沉降速率(mm/s)，比较的大小，分析循环荷载的频率和幅值对道床沉降速率的影响，如图6所示。

从图6中可以看出，载荷幅值为3 kN时，5～20 Hz荷载频率之间道床沉降速率变化较小；载荷频率大于20 Hz时，道床沉降速率变化较大。载荷幅值为5 kN，载荷频率大于10 Hz时，道床沉降速率变化较大。表明：循环荷载频率和荷载幅值对道床沉降速率的影响是关联的、叠加的。在一定的荷载幅值下，荷载频率越高，道床的沉降速率增加得越快。

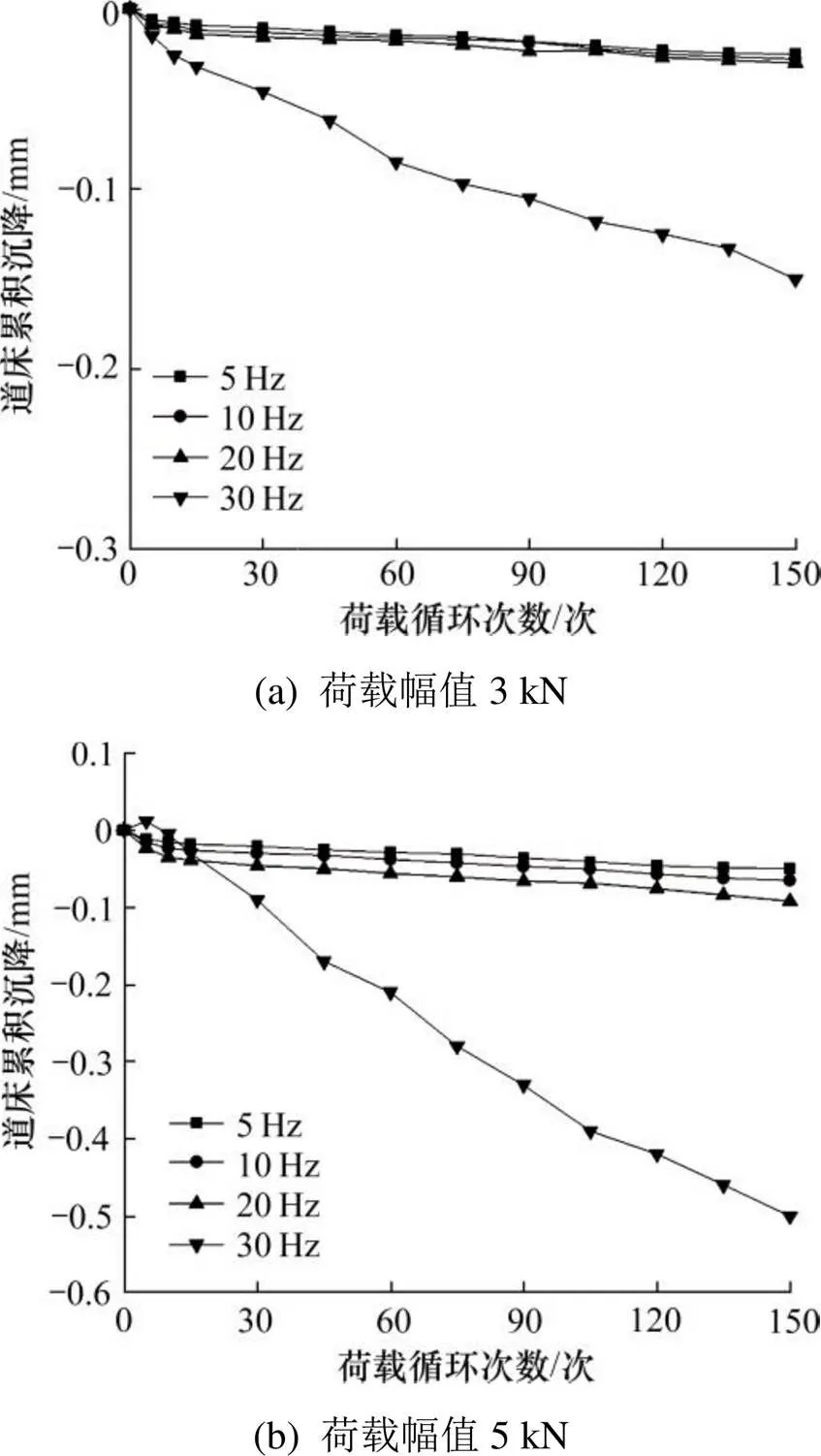
图5 不同频率循环荷载下道床的累积沉降

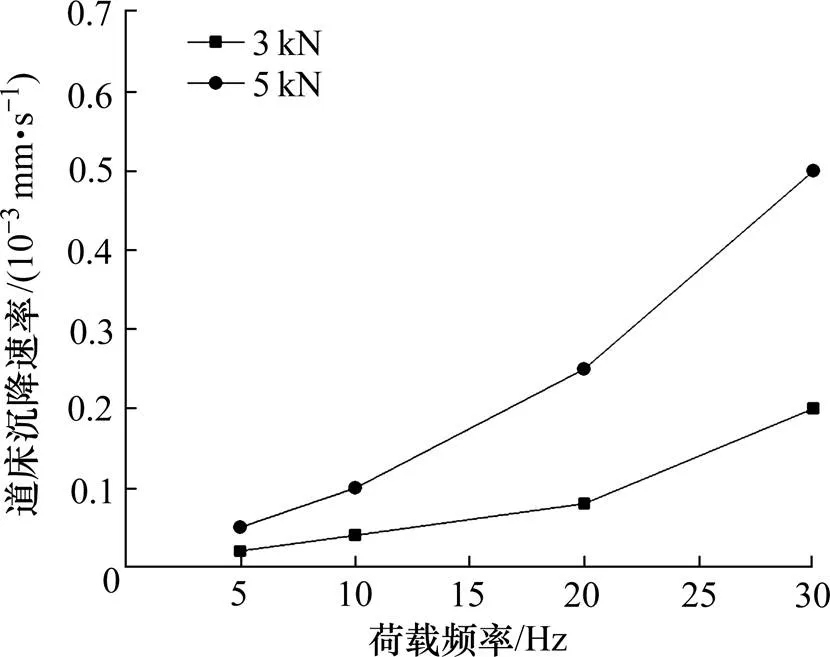
图6 道床沉降速率与荷载频率的关系

3.3 循环荷载下道床力学性能分析

道床的力学性能对有砟轨道的影响程度较大，分析循环荷载下道床的力学性能至关重要。密实度、横纵向阻力、道床的支撑刚度等均可表现道床的力学性能。本研究主要分析循环荷载下道床的垂向刚度，道床的垂向刚度表现为道床垂直方向上的受力与位移之间的关系。通常对道床垂向刚度的研究指道床所受的载荷力和位移量的增量比值，可简化为轨枕的受力和位移的比值，如图7所示。

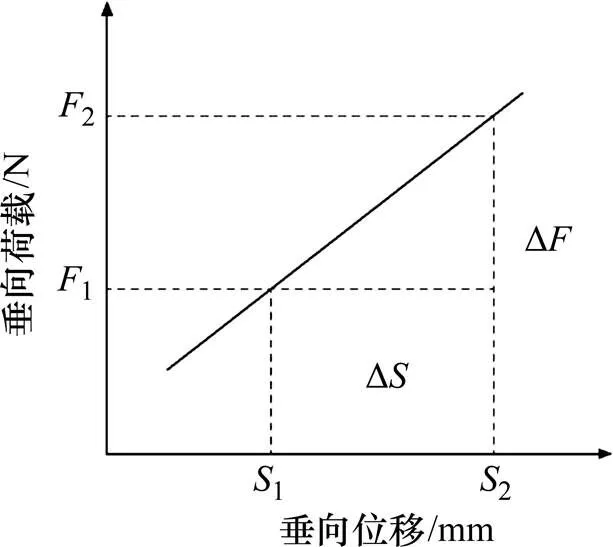
图7 道床的垂向刚度示意

道床的垂向荷载为，垂向位移为，得到垂向刚度为：

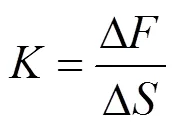
由式(3)可知，道床的垂向刚度可由图7中曲线的斜率表示。在循环荷载的作用下，道床的受力曲线是波动性的，即道床的垂向刚度也是在不断地变化，但总体变化形式不变。不同循环荷载频率下加载500次时，道床的受力−位移曲线如图8所示。

从图8中可以看出，在循环荷载频率为10 Hz和20 Hz时，受力−位移曲线变化频率较慢，道床垂向刚度逐渐增大，且两者的变化曲线较为相似。当频率为30 Hz时，受力−位移曲线变化频率加快，道床垂向刚度显著增大。

4 结论

1) 在研究循环荷载的频率和幅值对道床沉降影响过程中，循环荷载频率不超过20 Hz时，荷载频率对道床的沉降量及沉降速率的影响程度较小；循环载荷频率为30 Hz时，道床的沉降量及沉降速率的影响显著增大。

2) 循环荷载幅值越大，道床的沉降及沉降速率也越大；荷载频率越大，道床的垂向刚度越大。

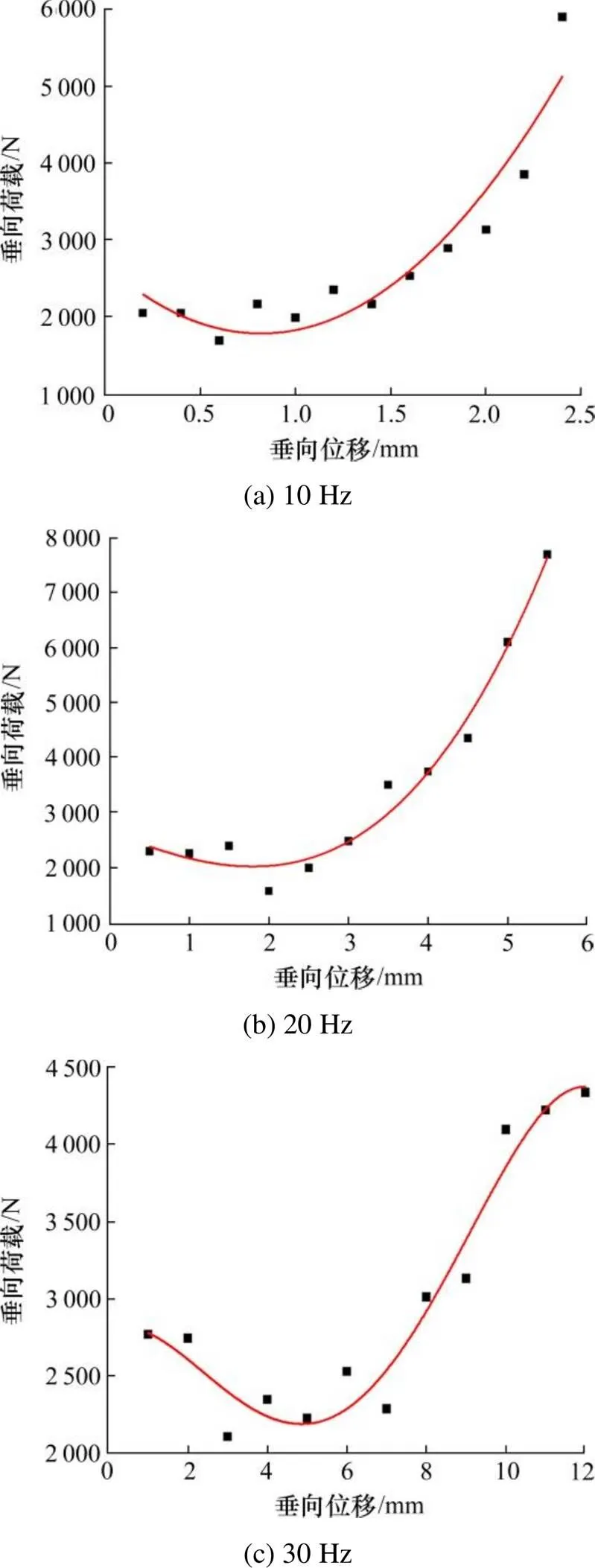
图8 不同循环荷载频率下道床的受力--位移曲线

[1] 高建敏,翟婉明,徐涌.有碴轨道下沉变形参数影响分析[J].交通运输工程学报,2007,7(4):15−20.(GAO Jian-min, ZHAI Wan-ming, XU Yong. Analysis of parameters' effects on settlement of ballasted track[J]. Journal of Traffic and Transportation Engineering, 2007, 7(4): 15−20. (in Chinese))

[2] Tutumluer E, Qian Y, Hashash Y M A, et al. Discrete element modelling of ballasted track deformation behaviour[J]. International Journal of Rail Transportation, 2013,1(1/2):57−73.

[3] Al-Saoudi N K S, Hassan K H. Behaviour of track ballast under repeated loading[J]. Geotechnical and Geological Engineering,2014,32(1):167−178.

[4] 姜卫利,范俊杰.散粒体道床离散单元法分析[J].铁道学报,2001,23(4):98−101.(JIANG Wei-li,FAN Jun-jie.Using of distinct element method to analyze granular ballast bed[J].Journal of the China Railway Society,2001,23(4): 98−101.(in Chinese))

[5] 张徐,赵春发,翟婉明.铁路碎石道砟静态压碎行为数值模拟[J].西南交通大学学报,2015,50(1):137−143. (ZHANG Xu, ZHAO Chun-fa, ZHAI Wan-ming. Numerical analysis of static crushed behavior of railway ballast[J]. Journal of Southwest Jiaotong University, 2015, 50(1):137−143.(in Chinese))

[6] Cundall P A. A computer model for simulating progressive large-scale movements in blocky rock systems[J]. Proceedings of Symposium of the International Society of Rock Mechanics, 1971, 1(ii-b): 11−8.

[7] Potyondy D O, Cundall P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(8):1329−1364.

[8] 郑瑶,董为民,周陶勇,等.道砟级配对捣固的效果影响及其参数优化[J].武汉理工大学学报:交通科学与工程版, 2019, 43(5): 937−941. (ZHENG Yao, DONG Wei-min, ZHOU Tao-yong, et al. Influence of ballast grading on tamping effect and parameter optimization[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2019, 43(5): 937−941.(in Chinese))

[9] 葛继平,沈磊,王志强,等.高速铁路模型箱梁静力非线性和动力损伤关系研究[J].武汉理工大学学报:交通科学与工程版,2013,37(6):1171−1175.(GE Ji-ping,SHEN Lei, WANG Zhi-qiang, et al. Research on the relationship of the dynamic characteristics and static performance of high-speed railway box girder model under repeated loading[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2013, 37(6): 1171−1175.(in Chinese))

[10] 丁秀丽,李耀旭,王新.基于数字图像的土石混合体力学性质的颗粒流模拟[J].岩石力学与工程学报,2010,29(3): 477−484. (DING Xiu-li, LI Yao-xu, WANG Xin. Particle flow modeling mechanical properties of soil and rock mixtures based on digital image[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 477−484. (in Chinese))

[11] 庞逸群. 基于Logistic曲线的地铁工程沉降预测模型研究[J]. 现代测绘, 2020, 43(2): 20−22. (PANG Yi-qun. Research on settlement prediction model of subway engineering based on logistic curve[J]. Modern Surveying and Mapping,2020,43(2):20−22.(in Chinese))

[12] 彭华,杨志蔚,曹全,等.盾构下穿铁路碎石道床沉降规律及施工参数控制[J].工程力学,2019,36(S1):222−228. (PENG Hua, YANG Zhi-wei, CAO Quan, et al. The settlement law of railway ballast beds traversed by a shield tunnel and the control of shield construction parameters[J]. Engineering Mechanics, 2019, 36(S1): 222−228.(in Chinese))

[13] 孔祥勋,田爽,唐亮,等.重载铁路高路堤沉降预测及影响因素分析[J].北京交通大学学报,2019,43(3):26−34. (KONG Xiang-xun, TIAN Shuang, TANG Liang, et al. Prediction of deformation and analysis of influence factors in heavy-haul railway high embankment[J]. Journal of Beijing Jiaotong University, 2019, 43(3): 26− 34.(in Chinese))

[14] 魏明鉴,许平,周陶勇,等.基于离散元法的道砟胶固化道床力学特性模拟[J].交通科学与工程,2020,36(2):92−97. (WEI Ming-jian, XU Ping, ZHOU Tao-yong, et al. Simulation study on mechanical properties of ballast bed solidified by ballast glue based on discrete element method[J]. Journal of Transport Science and Engineering, 2020,36(2):92−97.(in Chinese))

A discrete element analysis of railway ballast bed under cyclic loading

ZHANG Shuai-hui, ZHOU Tao-yong, XU Ping, ZHANG Ya-qing, XIA Jian-jun

(Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China)

To explore the variation laws of cumulative settlement in high-speed ballasted, the discrete element software PFC3D5.0 was used to establish a three-dimensional discrete element model of ballast bed with loose grain in graded high-speed railway. The cyclic load frequencies were set at 5 Hz, 10 Hz, 20 Hz and 30 Hz, and the load amplitudes were set at 3 kN and 5 kN. A total of 8 load conditions were selected for numerical simulation test. By analyzing the mechanical properties of the ballast bed, the influence of frequency and amplitude of cyclic load on the ballast bed settlement was discussed. The results show that when the cyclic load frequency does not exceed 20 Hz, the load frequency has little influence on the settlement and settlement rate of ballast bed. When the cyclic load frequency is greater than 30 Hz, the settlement and settlement rate of the ballast bed will increase significantly. The greater the amplitude of the cyclic load, the greater the settlement amount and rate of the ballast bed. The greater the frequency of the cyclic load, the vertical stiffness of the ballast bed will increase.

railway ballast; cyclic loading; discrete element method; ballast settlement

U213.7

A

1674 − 599X(2021)01 − 0007 − 06

2020−07−14

昆明理工大学引进人才科研启动基金项目(KKSY201855004)；昆明理工大学分析测试基金(2019M20182203070)

张帅辉(1994−)，男，昆明理工大学硕士生。