基于PCA-BP原理预测公路最终沉降量
2021-04-23甘海龙
□ 甘海龙
1 引言
近年来,随着我国城镇化建设步伐的加快,各地城市中高等级道路在设计与施工方面取得了很大的进步。作为道路主体的路基,对其综合稳定技术的研究也取得了新的进展。道路路基综合稳定性及其强度是路面工程质量的重要保证。其施工过程中如果施工方法不当或者用料不合理,对路基的稳定性均会产生不良的影响,导致路基在使用过程中极易出现路基沉陷、边坡滑塌等问题。因此道路路基最终沉降量的研究对今后道路的养护维修以及交通的正常运行具有重要意义。此外,研究如何科学计算路基的最终沉降量,具有良好的社会效益和极大的经济、技术价值。
2 最终沉降量的计算方法
目前预测路基最终沉降量的方法主要有经验公式法、Asaoka法、遗传算法、灰色系统法和神经网络预测法[1]。
孙常青[2]等提出一种双曲线零点平移拟合法来确定最终沉降量;李凡[3]等建议在采用传统的双曲线法推算软土地基最终沉降量的同时,可运用 Asaoka推算法进行校核;朱胜利[4]采用实测沉降曲线推算地基最终沉降量的新型双曲线型表达式;李凡[5]等提出利用小波神经网络预测高速公路软土地基的最终沉降量的方法。
3 BP神经网络
BP神经网络是包含多个隐含层的网络,具备处理线性不可分的能力。BP神经网络是前向神经网络的核心部分,也是整个人工神经网络体系的精华,广泛用于分类识别、逼近、回归、压缩等领域。在实际应用中,大约80%的神经网络模型采用了BP神经网络或者BP神经网络的变化形式。一个一般的三层结构BP网络的结构图如图1所示。
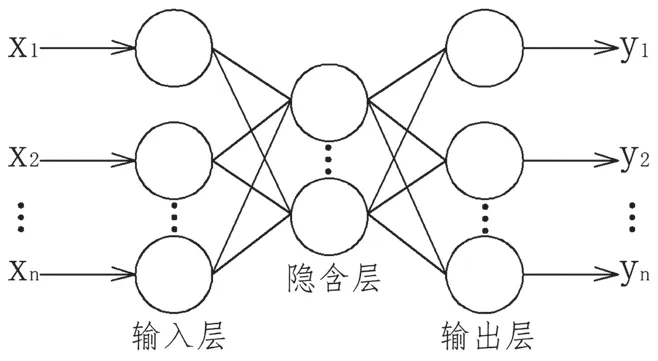
图1 BP神经网络结构示意图
BP网络的传递函数为
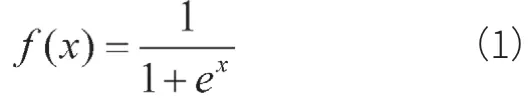
误差函数为
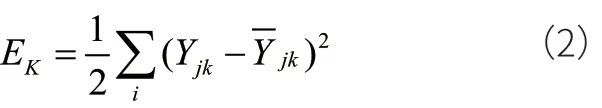
总误差为
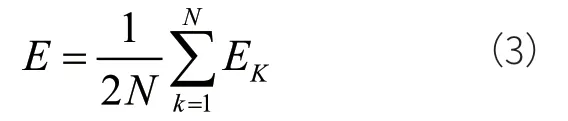
隐层与输入层的权值调整量为
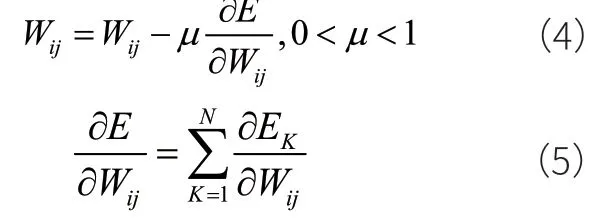
4 PCA-BP神经网络预测公路最终沉降量模型的建立与应用
公路最终沉降量与软土层厚度、软土压缩模量等因素有直接关系,主要因素有软土层厚度、软土压缩模量、硬层厚度、硬层压缩模量、路堤宽高比、路基施工工期、竣工时沉降量等。基于以上7个参数建立PCA-BP网络预测公路最终沉降量的神经网络模型。首先使用主成分分析法对原始输入样本影响因子进行降维处理,将降维后的变量作为BP神经网络的输入样本,通过迭代计算后输出结果,建立基于PCA-BP网络的公路最终沉降量预测模型,PCA-BP建模流程见图2。
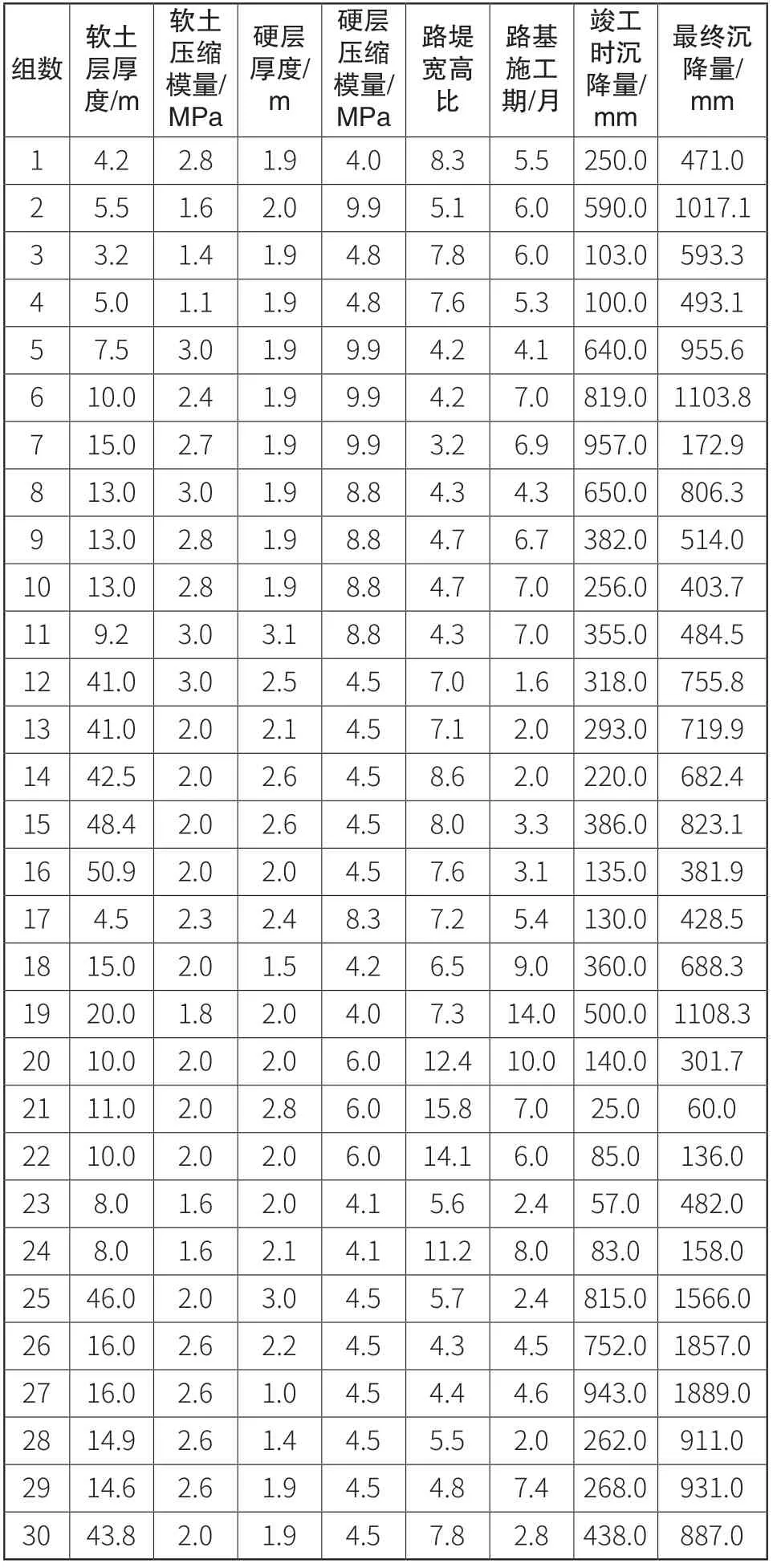
表1 网络输入数据

图2 PCA-BP建模流程
5 网输入数据分析
文献[6]采集了30组全国各地公路施工数据与最终沉降量,见表1。
相关计算结果如表2—表4所示。由表2可知:输入的样本数据中部分指标间存在多重共线性,为提高网络模型预测精度,需利用主成分分析法对输入样本进行降维处理。

表2 各因素间的相关系数矩阵
6 主成分分析
借助MATLAB得到相关系数矩阵特征值与主成分荷载,得到各成分的贡献率(见表3) ,主成分荷载矩阵(见表4)。由表3可知: 前4个主成分累计方差贡献率已大于85%,达到了主成分方差占总方差85%以上的要求。因此通过主成分分析,原始数据的7个主成分可以降为4个,故只需用第1至第4主成分PC1-PC4代替原始输入。
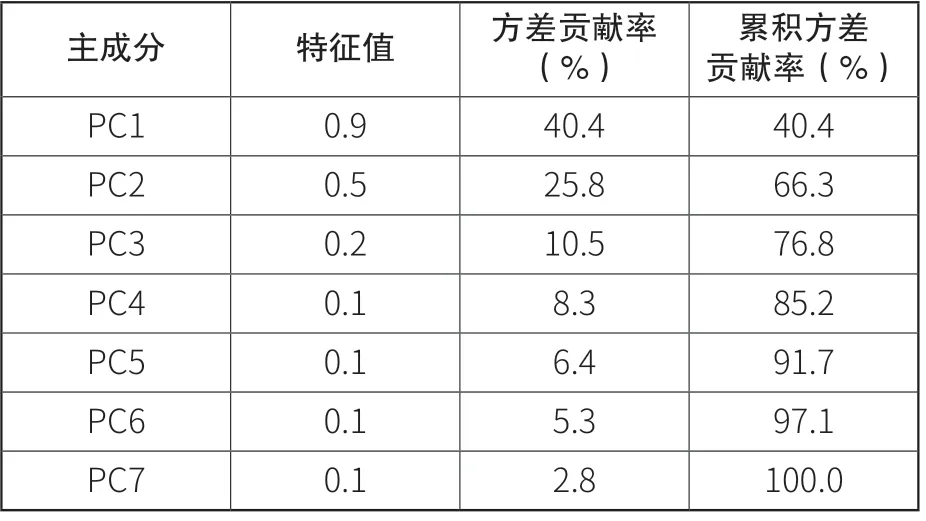
表3 PCA分析结果

表4 主成分因子荷载矩阵
7 PCA-BP网络的设计、训练与预测
以上文PC1-PC4作为4个输入因子,最终沉降量为1个输出因子,构建神经网络。BP神经网络隐含层的节点数对于神经网络的整体性能非常重要,所以神经网络隐含层节点数的确定非常关键,隐含层节点数的经验计算公式为:
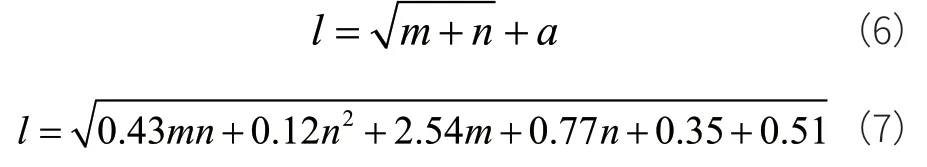
式中m、n分别为输入节点数和输出节点数;a为1至10之间的常数。本文根据式(6)与式(7),结合神经网络的多次测试结果,最终确定隐含层的最佳节点数为6。
神经网络的训练与预测采用如下规则:从输入数据中随机提取75%的数据作为训练集,从输入数据中随机提取15%的数据作为验证集,从输入数据中随机提取15%的数据作为测试集。当验证集均方误差不再持续降低时,网络结束训练。神经网络的训练方法通常有以下几种:BP方法、delta-bar-delta方法、最速下降法、Quickpro方法、拟牛顿法和LM法。
本网络的训练采用拟LM法,即Levenberg-Marquardt(以下简称“LM法”)。LM法改善了高斯—牛顿方法中将误差的一阶和二阶导数结合起来所隐含的,仅通过反复学习率很难解决的问题的解决方案。LM法不是调整学习率ε,而是把它设置成一个不变的值,在二阶导数项里再添加一个新项eλ,这里e是自然对数。
神经网络的最佳验证误差如图3所示,由图可知,使用LM法训练神经网络后,神经网络的迭代步数非常少,仅需8步就完成了网络的训练,并在迭代步数为2时得到神经网络的最佳验证均方误差值为0.03145,神经网络的训练集的均方误差在整个训练过程中持续减小。

图3 神经网络工作性能
神经网络模型的训练集、验证集、测试集及所有数据的线性回归分析如图4所示,由图可知,神经网络4个子集的期望输出与网络输出具有较高的拟合度,说明神经网络模型的整体工作性能良好。

图4 线性回归分析
神经网络的预测结果与预测误差如表5所示,表中公路最终沉降量值为10组随机作为测试集与验证集的公路最终沉降量神经网络输出结果经过反变换计算的结果。
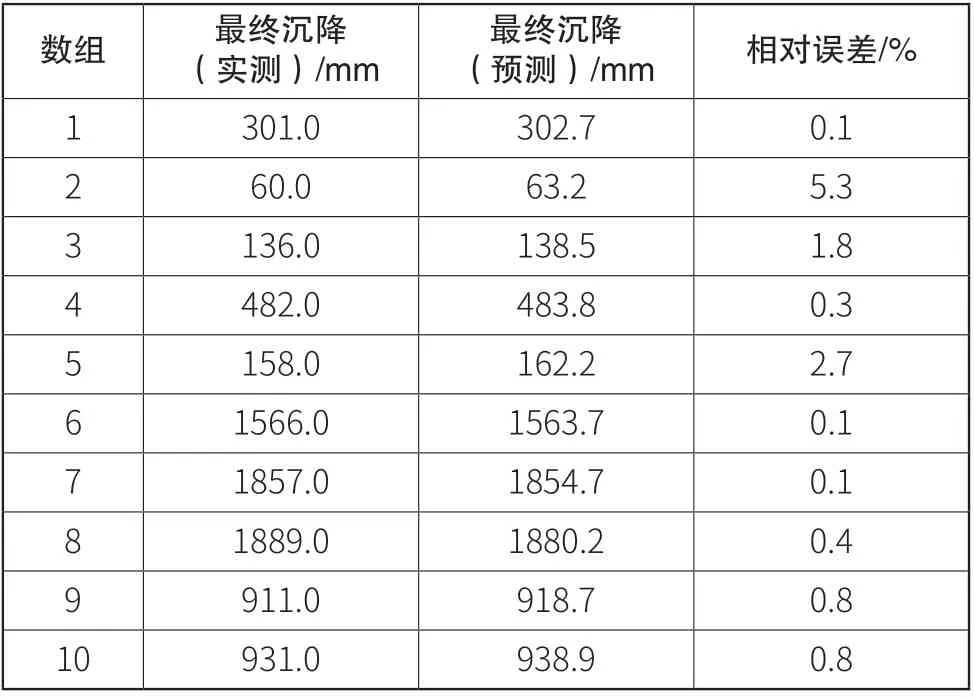
表5 误差表
8 结论
软土地基区公路最终沉降量是公路安全性评估的重要参数,影响公路最终沉降量的因素主要有软土层厚度、软土压缩模量、硬层厚度、硬层压缩模量、路堤宽高比、路基施工工期、竣工时沉降量。本文利用神经网络预测公路最终沉降量,得出以下结论:
(1)主成分分析法(PCA)有效解决了神经网络原始输入变量间的多重共线性,同时减少了BP 神经网络的输入神经元个数,在保证神经网络预测精度的同时有效地简化了神经网络的规模,表明PCA-BP网络模型对公路最终沉降量预测具有改进意义。
(2)较之单一的神经网络预测模型,PCA-BP神经网络模型的预测误差较小。基于PCA-BP神经网络建立的公路最终沉降量预测模型,其预测结果良好。表明PCA-BP神经网络预测模型能够对公路最终沉降量提供可靠、科学的指导。
