Fatigue life evaluation of girth butt weld within welded caststeel joints based on the extrapolation notch stress method

Wei Zezhong Jin Chuanling Jin Hui

(1Jiangsu Key Laboratory of Engineering Mechanics, Southeast University, Nanjing 211189, China)(2School of Civil Engineering, Southeast University, Nanjing 211189, China)(3Jiangsu Frontier Electric Technology Co., Ltd., Nanjing 211102, China)

Abstract：The fatigue life evaluation of the girth butt weld within the welded cast steel joint was studied based on the extrapolation notch stress method. Firstly, the mesh sensitivity of the finite element model of the welded cast steel joint was analyzed to determine the optimal mesh size. Based on the stress field analysis of the finite element model of the welded cast steel joint at the weld toe and weld root, the sharp model of the extrapolation notch stress method was applied to derive the effective notch stress of the rounded model belonging to the effective notch stress method, in which the key problem is to calculate the extrapolation point C, and the extrapolation point C has an exponential function relationship with the geometric parameters of the welded cast steel joint. By setting different values of geometric parameters, the corresponding value of parameter C is calculated, and then the functional relationship between the extrapolation point C and the geometric parameters can be obtained by the multiple linear regression analysis. Meanwhile, the fatigue life evaluation of the girth butt weld within welded cast steel joints based on the effective notch stress was performed according to the guideline recommended by the IIW (International Institute of Welding). The results indicate that the extrapolation notch stress method can effectively simplify the process of calculating the effective notch stress and accurately evaluate the fatigue life of the girth butt weld within welded cast steel joints.

Key words：welded cast steel joint; girth butt weld; extrapolation notch stress method; effective notch stress method; fatigue life evaluation

Cast steel joints (CSJs) have broad application prospects[1-7], such as in bridge engineering, offshore oil platforms, wind turbine towers, cranes, and other engineering fields. The CSJ acts as a connecting member between steel pipes and can solve the welding problem that occurs in the intersection portion within steel tubular joints. The welded CSJ is divided into the base material part and the weld seam part, so its mechanical performances are determined by the two parts above. The mechanical properties of the welded CSJ mainly include static performance and fatigue performance. Regarding the static performance of CSJ, many research studies[8-11]have been carried out worldwide. The fatigue performance of the welded CSJ is complicated[12]. As the welding process leads to the initial defects within the weld part, the fatigue failure of welded structures is ultimately determined by the fatigue performance of the weld seam part[13-19], and the fatigue problem of the welded cast steel joint is no exception[1,20]. The results of recent experimental studies[6-7,20-21]indicate that the fatigue problem of welded cast steel joints is located at the weld seam part. Studies on the fatigue life evaluation of the welded CSJ are mainly based on the nominal stress parameter[12], for complicated welded CSJs under complex loading conditions. There is no consistent way to define the nominal stress within the welded CSJ. Therefore, the fatigue life evaluation of welded CSJs needs to be further addressed.

The effective notch stress method (ENSM) is widely applied in the fatigue life evaluation of welded structures[22]. Effective notch stress can represent the local stress state of the welded structure in fatigue life evaluation. Only oneS-Ncurve is needed for various types of steel welded joints[22]in the fatigue life evaluation, thus avoiding the subjectivity and uncertainty of selecting differentS-Ncurves for different welded structures under different load modes in the nominal stress method and the structural hot spot stress method. Furthermore, the effective notch stress method can be applied in the case of weld root failure, which is currently difficult to solve using the structural hot spot stress method[23].

The calculation of the effective notch stress relies entirely on numerical finite element simulations, which require creating a virtual radius of 1 mm (in the case of plate thickness greater than 5 mm) at the weld toe or the weld root and a very fine element mesh should be satisfied. Compared with the nominal stress method and the structural hot spot stress method, a fine finite element model greatly increases the mesh work of the finite element model. In this article, an extrapolation notch stress method proposed by Pradana et al.[24]is used to simplify the process of calculating the effective notch stress at the girth butt weld of welded cast steel joints, and its applicability of calculating effective notch stress at the root of welded CSJ is verified. Then, the fatigue life evaluation of the girth butt weld within welded cast steel joints is carried out according to the guideline recommended by the IIW[22].

1 The Extrapolation Notch Stress Method

The process of calculating the effective notch stress by the extrapolation notch stress method is similar to that of using the extrapolation strategy to determine the structural hot spot stress at the weld toe of the welded structure in the IIW specification[25]. In the procedure of calculating the effective notch stress by the extrapolation notch stress method, it is not necessary to establish a virtual notch radius of 1 mm at the weld toe/root combined with very fine finite element mesh, thus greatly simplifying the mesh work of finite element models, especially for welded structures with complex geometry, such as a welded CSJ. The detailed content of the extrapolation notch stress method for calculating the effective notch stress is described below, and more information about this method can be found in Refs.[24,26-27].

1.1 Basic theory

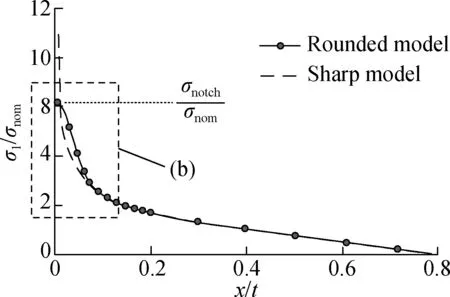
The stress field of the finite element model exhibits stress singularity at the vicinity of the weld toe or the weld root in welded structures. The irregular geometry of the weld seam and the microscopic defects within the weld seam lead to the notch effect at the weld toe or the weld root. According to the linear elastic theory of the material, the calculated notch stress at the weld toe or the weld root approaches infinity. However, materials at the local weld toe or the weld root exhibit obvious anisotropy properties, thus directly constraining and reducing the local peak stress at the weld toe or the weld root.Therefore, the notch stress solved by the notch stress field equation does not represent the actual stress state at the weld location. Sonsino et al.[22]proposed the effective notch stress parameter to represent the actual stress state at the notch location (weld toe or weld root). The peak stress of the original notch location was weakened by increasing the notch radius. Therefore, a rounded model with an amplified radius at the notch location can portray the actual stress state at the weld toe or the weld root, and is applied to analyze the fatigue behaviors of welded structures. Pradana et al.[24]proposed a new way, i.e. the extrapolation notch stress method, to determine the effective notch stress with the sharp model. Fig.1 shows the basic theory of this new method.

(a)

The idea of the extrapolation notch stress method[24]comes from the comparison between the stress field of the presence of the virtual notch radius (rref=1 mm) and that of the absence of the virtual notch radius (rref=0 mm). Two finite element models[27](the rounded model and sharp model) with identical geometric dimensions, load conditions, and element mesh sizes were created, and the difference is that the rounded model includes a virtual notch radius (rref=1 mm) at the weld toe, and the sharp model is not (rref=0 mm). It is shown in Fig.1 that the stress of the sharp model at the weld toe (rref=0 mm) is infinite and not convergent; on the contrary, the stress of the rounded model corresponding to the effective notch stress method approaches a constant maximum value at the weld toe (rref=1 mm). It can be seen from Fig.1(a) that, outside the distance of 0.2t(tis the thickness of the steel pipe) from the weld toe, the curves of the maximum principal stress (here the maximum principal stress was normalized by the nominal stress) calculated using the rounded model and the sharp model coincide with each other and maintain a linear relationship with the distance from the weld toe. It can be seen from Fig.1(b) that, in the double logarithmic coordinate system, the stress of the sharp model is still linear with the distance from 0.04tto 0.2t. Then, the linear curve part is extrapolated to the weld toe direction and intersects with the stress curve of the rounded model at the extrapolation pointC. Since the effective notch stress calculated by the rounded model tends to be constant near the weld toe, it can be seen from Fig.1(b) that the extrapolation pointCis located precisely in the stable region of the stress curve of the rounded model. When parameterCis obtained, the effective notch stress of the rounded model at the weld toe can be derived from the stress curve of the sharp model at locationC. Pradana et al.[24,26]verified that the stress curve of the rounded model and that of the sharp model intersect within the distance of 0.02tfrom the weld toe, so in this paper, the study of the welded CSJ finite element model focuses on the stress field within the distance of 0.02tfrom the weld toe and the weld root.

1.2 Calculation steps

As shown in Fig.1(b), it is indicated that the linear part of the stress field of the rounded model and that of the sharp model are on top of each other from 0.04tto 0.2t, so the linear part of the curve can be expressed as

logm=a+blogn

(1)

Letm=σ1/σnom,n=x/t, whereσ1is the maximal principal stress, andσnomis the nominal stress. Then, substitutingm,ninto Eq.(1), we derive

(2)

Removing the logarithmic symbol on both sides of Eq.(2), we obtain[24]

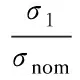
(3)

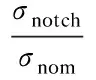
(4)

whereAandBare the coefficients, and the nominal stress[24]σnomis the stress resulting from the applied external load, which ignores the effect of the local notch effect. Settingx/t=Cand substituting it into Eq.(3), the effective notch stressσnotchat the weld toe can be obtained by Eq.(4)[24]. ParameterCis related to the structural geometric parameters and load modes. Letα,β,γ,ζ,η, etc. be the structural geometric parameters, and thenCcan be expressed as[24]

C=f(αβγζη)

(5)

To apply Eq.(4) for calculating the effective notch stressσnotch, the key problem is to determine coefficientsA,B, and the extrapolation pointC. The effective notch stressσnotchat the weld toe can be solved by the rounded model, and coefficientsA,Bcan be defined by fitting the linear part (from 0.04tto 0.2t) of the stress curve of the sharp model, and then the value ofCcan be obtained by the inverse analysis of Eq.(4). By setting different geometric parameter values, parameterCcan be also calculated by Eq.(4), and then the relationship betweenCand the geometric parameters in Eq.(5) can be established by fitting. It should be noted that the extrapolation notch stress method is different from the effective notch stress method, and it is necessary to verify the mesh sensitivity problem of the finite element model when performing the effective notch stress calculation through the extrapolation notch stress method.

2 Application of the Extrapolation Notch Stress Method in Welded Cast Steel Joints

2.1 Mesh size definition

A typical welded cast steel joint[6-7]is shown in Fig.2, which consists of a cast steel pipe, backing plate, weld seam, and connecting steel pipe. The elastic modulusE1and Poisson’s ratio of cast steel material are equal to 211 GPa and 0.29, respectively. The elastic modulusE2of the steel pipe is 206 GPa, and Poisson’s ratio is 0.3. The mechanical properties of the backing plate are consistent with those of the steel pipe. A tension loadFof 20 MPa is applied to the end of the connecting steel pipe of the welded cast steel joint shown in Fig.2(a), and the end of the cast steel pipe is fixed. As shown in Fig.3, the Solid 185 element is chosen to mesh the finite element model of the welded cast steel joint. The maximum principal stress (σ1) is selected for the stress analysis for both the rounded model and the shape model.

(a)

The optimal mesh size is determined by controlling variables. As shown in Fig.3(a), firstly, the length of the element (elength) is maintained at a constant value of 0.01t, and the thickness of the element is changed, and then its effect on the normalized max principal stress (σ1/σnom) distribution is studied. As shown in Fig.4, the stress within the distance of 0.25tfrom the weld toe is selected for the mesh sensitivity analysis of the depth of the element. It can be seen from Fig.4 that whenedepthis less than or equal to 0.01t, the linear part of the normalized maximal principal stress curve of the sharp model coincides with that of the rounded model. Therefore,edepthtakes the value of 0.01tin the following analysis.

(a)

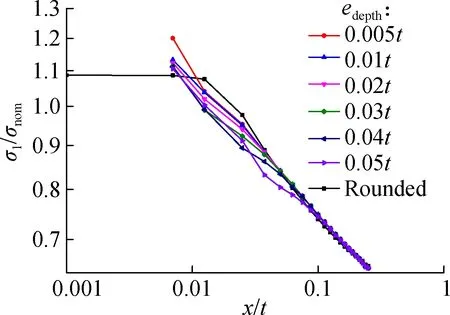
Fig.4 Normalized stress corresponding to finite element models with elements of different thicknesses

The element lengthelengthcan be determined by its influence on coefficientsA,B, parameterC, and the effective notch stress. According to the sharp model, the normalized maximal principal stress of all nodes at the linear extrapolation zone (0.04t-0.2t) is logarithmically fitted to quantify coefficientsaandbin Eq.(1), and then coefficientsAandBcan be obtained by Eq.(3). As the effective notch stress can be obtained by the rounded model,Ccan be calculated by Eq.(4).

To simulate the actual geometry of the welded cast steel joint in engineering applications, the outer diameter of the welded cast steel joints(d) studied in this section is equal to 160 mm, and the thicknesses of the cast steel section (t0) are 16 and 14 mm, respectively. The thicknesses of the steel pipe (t1) are 8 and 6 mm, respectively. The element lengthelengthis increased from 0.005tto 0.05t, and the result is shown in Fig.5. As can be seen from Figs.5(a) to (c), the smaller the element length, the more the parametersA,B,Ctend to be constant. As can be seen from Fig.5(d), there is almost no correlation between the normalized effective notch stress and the element lengthelength. For computational efficiency,elengthshould not be too small. Therefore, it is set to be 0.01tin the following analysis.

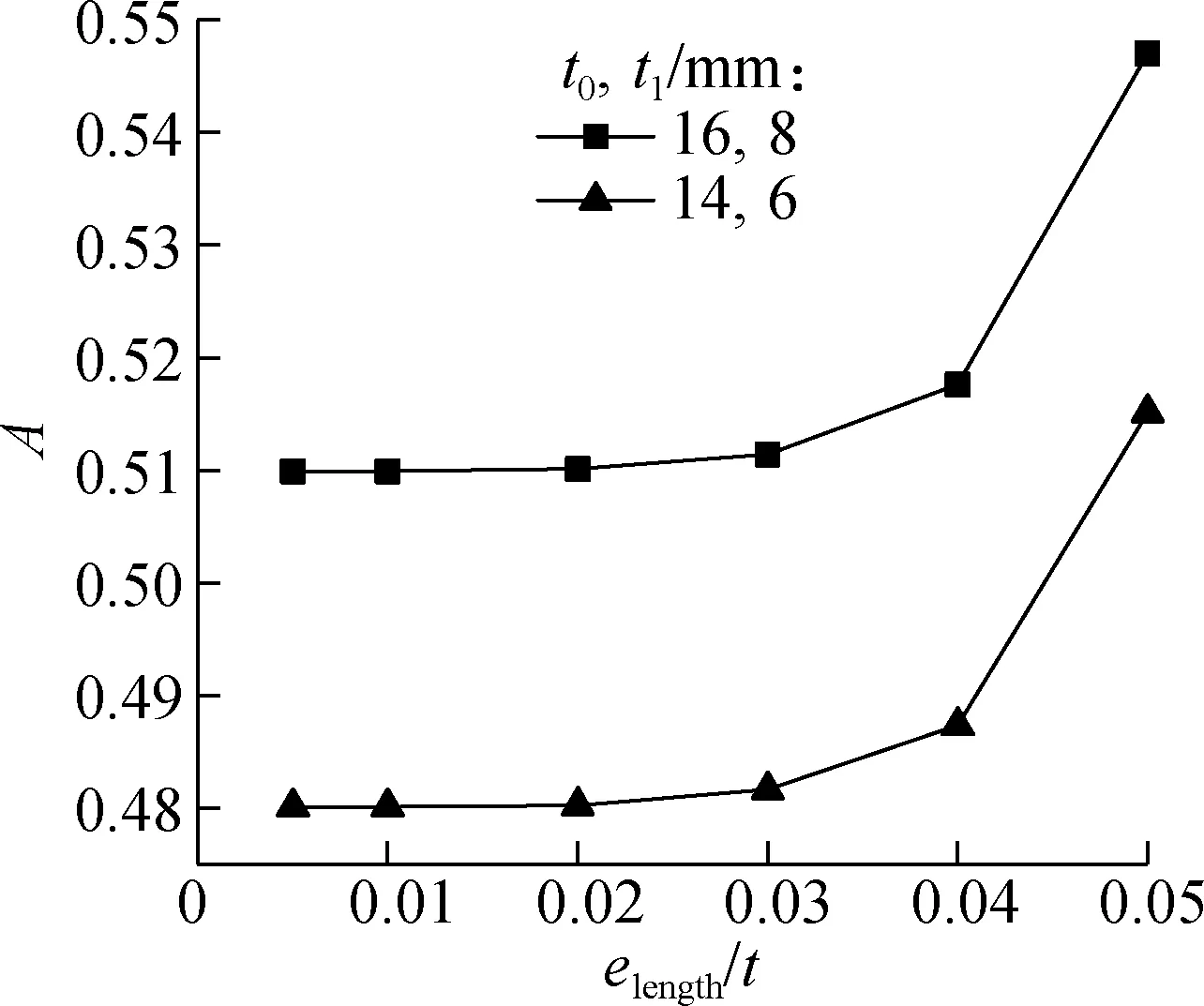
(a)

2.2 Calculation of effective notch stress at the weld toe

Tab.1 lists the main geometric parameters of the welded cast steel joint, including the thickness of the cast steel pipet0, the thickness of the connecting steel pipet1, the outer diameter of the connecting steel pipe and the cast steel piped. For convenience,t0,t1,dare replaced byα(t0/tref),β(t1/tref),γ(d/(2t1)), respectively, wheretrefis the reference thickness.

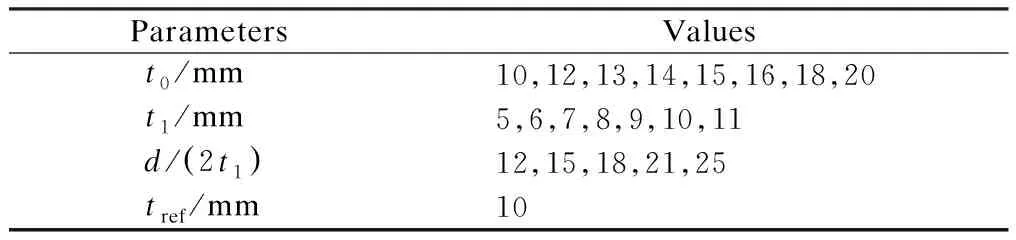
Tab.1 Geometry parameters of welded cast steel joint for calculating effective notch stress at the weld toe

As mentioned in Eq.(5), the following equation is used as the functional relationship between the value of extrapolation pointCand geometric parametersα,β,γ:

C=λ(α)X1(β)X2(γ)X3

(6)

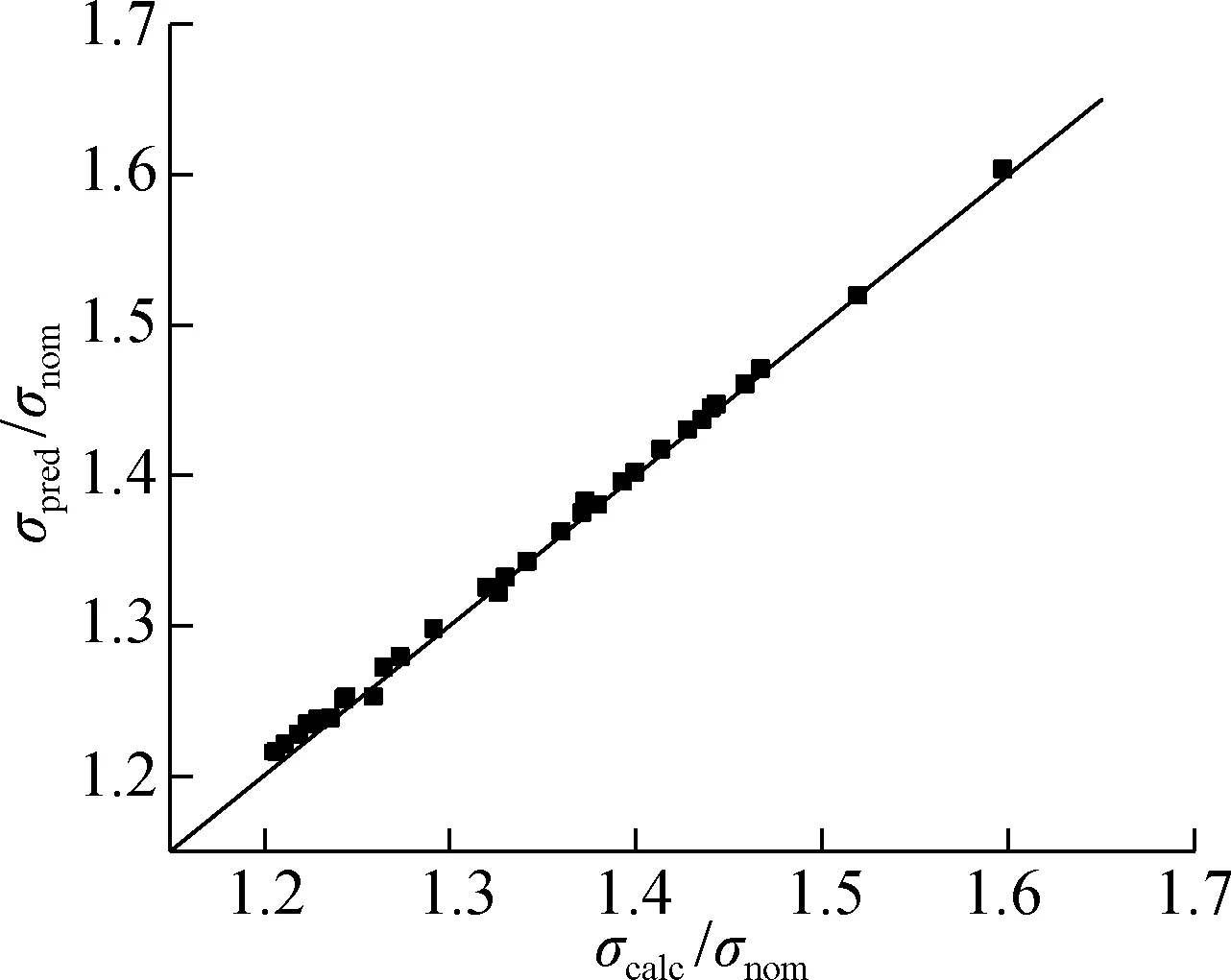
whereλ,X1,X2, andX3are the coefficients. By the multiple linear regression analysis performed using Matlab software, the coefficientsλ,X1,X2, andX3, and the correlation coefficientR2can be obtained, which are shown in Tab.2. The predicted effective notch stresses (σpred) calculated by Eq.(4) and Eq.(6) and the effective notch stresses (σcalc) calculated by the rounded model of the effective notch stress method under remote tension and remote bending are shown in Fig.6. It can be seen from Fig.6 that the ratio of the above two effective notch stresses is linear and proportional, and the error between the predicted value (σpred) and the actual value (σcalc) is small. It is verified that the extrapolation notch stress method can be applied to calculate the effective notch stress at the weld toe of welded cast steel joints.

Tab.2 Parameters of Eq.(6) and correlation coefficient R2 at the weld toe

2.3 Calculation of effective notch stress at the weld root

Tab.3 lists the main geometric parameters of the welded cast steel joint. The calculation of the effective notch stress at the weld root is similar to that at the weld toe.

(a)

Tab.3 Geometry parameters of welded cast steel joint for calculating effective notch stress at the weld root

The multiple linear regression analysis is performed using Matlab software to obtain the coefficients of Eq.(6) and the correlation coefficientR2, which are shown in Tab.4.The effective notch stressesσpredpredicted by the extrapolation notch stress method and the effective notch stressesσcalccalculated by the effective notch stress method under remote tension load are shown in Fig.7.The result of Fig.7 indicates that the relative error of the effective notch stresses calculated by the two methods at the weld root is greater than that at the weld toe due to the large stress concentration at the weld root but the stress ratio is still around 1.The extrapolation notch stress method can still be applied to calculate the effective notch stress at the weld root of the welded CSJ within a certain allowable error.

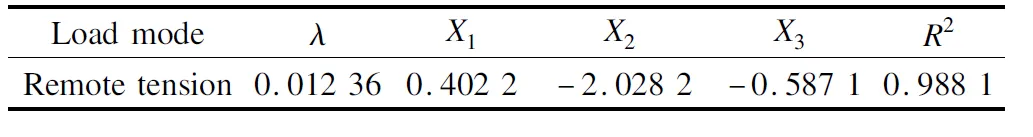
Tab.4 Parameters of Eq.(6) and correlation coefficient R2atthe weld root

3 Fatigue Life Evaluation of the Welded Cast Steel Joint

Fig.7 Comparison of effective notch stresses of two methods at the weld root under the remote tension load

The fatigue life evaluation accuracy of the extrapolation notch stress method and effective notch stress method is compared in this section. For steel welded structures,the IIW[28]recommended FAT225 curve as the designedS-Ncurve for the fatigue life evaluation based on the effective notch stress parameter Δσe. The inverse slopemof the curve is equal to 3, and theS-Ncurve is shown as

logN=13.558-3logΔσe

(7)

According to the welded cast steel joints applied in practical engineering cases, the fatigue life evaluation of four typical geometric sizes of the welded cast steel joints at girth butt weld shown in Fig.2 is carried out. The results are listed in Tab.5, and it can be seen from Tab.5 that the fatigue life predicted by the extrapolation notch stress method is very close to that by the effective notch stress method, and the maximum relative error is 4.4%. The effective notch stress range-fatigue life curves of the effective notch stress method and the extrapolation notch stress method are shown in Fig.8. It can be seen that the fatigue life of welded cast steel joints predicted by these two methods is nearly the same. The fatigue life evaluation by the extrapolation notch stress method is more conservative than that by the effective notch stress method, so the extrapolation notch stress method is also safe for the fatigue design of welded cast steel joints.

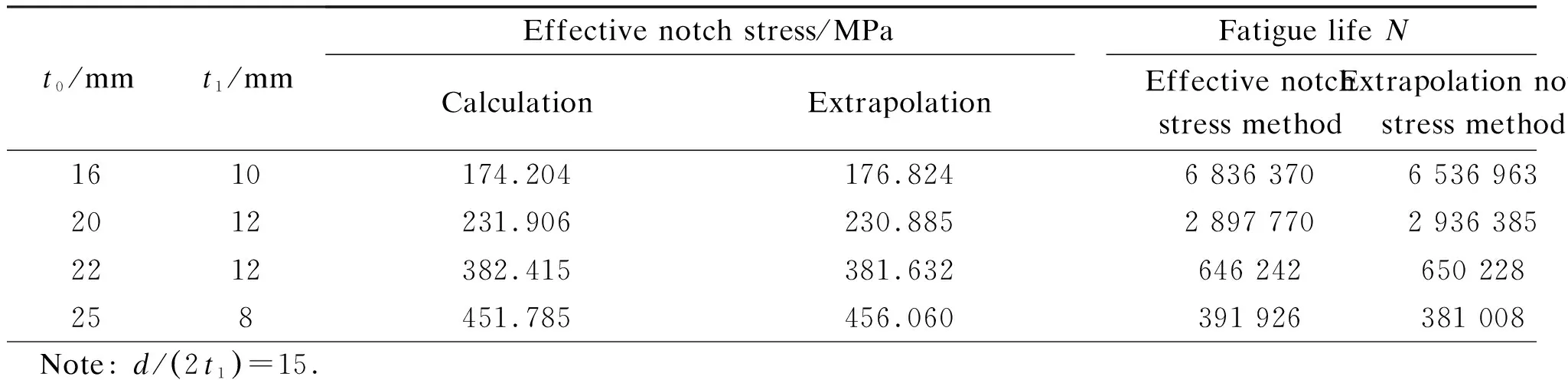
Tab.5 Fatigue life predicted by the effective notch stress method and extrapolation notch stress method

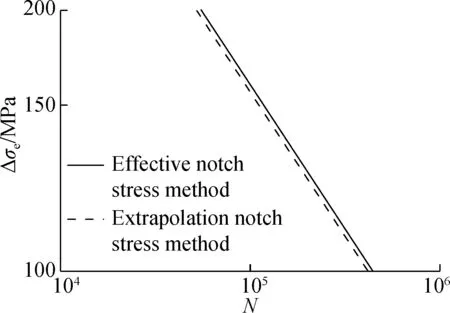
Fig.8 S-N curves of the two methods

4 Conclusions

1) When the extrapolation notch stress method is applied to calculate the effective notch stress at the weld toe or the weld root of welded cast steel joints, the length, and thickness of the element in the finite element model should be set to be 0.01tor less near the weld toe or the weld root, and the extrapolation zone should be 0.04t-0.2t. The extrapolation notch stress method has shown greater improvement in modeling convenience and computational efficiency than that of the effective notch stress method.

2) The geometry parameterst0,t1, anddof the welded cast steel joint are the main factors affecting the effective notch stress at the weld toe or the weld root under remote tension and remote bending load conditions. The extrapolation pointCis the most relevant to the thickness of the steel pipe. The effective notch stress calculated by the extrapolation notch stress method is consistent with that calculated by the effective notch stress method.

3) The fatigue life predicted by the extrapolation notch stress method is very close to that calculated by the effective notch stress method, and the extrapolation notch stress method is more conservative than the effective notch stress method, so it is safer for the fatigue design of welded cast steel joints.