面板堆石坝非线性变形特性及分区影响研究
2021-04-23茆大炜梅松华陈司宁梁经纬
茆大炜,梅松华,陈司宁,梁经纬
(1.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014;2.河海大学 水利水电学院,江苏 南京,210098;3.湖南省水利水电科学研究院,湖南 长沙 410007)
1 研究背景
我国的混凝土面板坝历经30多年的发展,建坝数量和高度均已位居世界首位。已建的水布垭、天生桥一级、洪家渡、紫坪铺等一批高面板坝工程在国内外均产生了一定的辐射影响力[1-2]。作为坝工建设的首选坝型之一,与其相关的不少工程问题仍需深入研究,如坝体变形控制[3]、坝体蠕变特性[4]、防渗体长期特性[5]、面板变形开裂[6]、面板接缝[7-8]及覆盖层影响[9]等。对于坝高200 m级及以上的高面板堆石坝,上述问题中坝体变形控制显得尤为重要[10]。目前坝工界普遍认为,堆石体分区和堆石料模量直接影响坝体和面板的变形与应力分布,从而决定大坝安全度。面板堆石坝设计坝料分区时,在充分利用当地材料的基础上,还要考虑坝体变形、坝坡稳定和渗流安全等要求,确保安全和经济协调统一。郦能惠[11]分析了天生桥一级和阿瓜密尔帕两座200 m级高面板堆石坝出现的一些工程问题,认为坝体分区设计除了遵循料源决定等基本原则以外,更应重视变形协调原则。徐泽平等[12]针对面板堆石坝工程中软岩堆石料的利用问题,指出通过合理布置软岩材料分区,可以有效扩大软岩利用区的范围。高照良等[13]指出为了有效控制坝体变形及其协调问题,坝料分区设计极为重要,并利用拓扑优化方法模拟了某高面板堆石坝断面,对坝料分区进行了优化研究。廖敏[14]对丫多河面板堆石坝不同材料分区进行了数值模拟。毛渐等[15]通过水布垭面板坝有限元计算,指出当主次堆石变形模量比相差2倍以内时,主次堆石分界线可偏向上游侧,此时坝体和面板的变形均较小。余小孔[16]认为主、次堆石料模量相差较大时,容易使面板变形性能变差,此时主次堆石分界线应偏向下游侧。李翠[17]研究指出主次堆石模量系数比不断增大会使坝体沉降变形减小,主堆石区对坝体变形影响显著。
本文在上述研究基础上,进一步扩大主次堆石分区及模量比变化范围,通过建立多个仿真模型,计算大坝竣工期、蓄水期及考虑长期流变后的变形特性,通过归纳总结,提出了堆石坝合理分区和模量比建议,供堆石坝优化设计时参考。
2 堆石料非线性本构模型及计算参数
2.1 邓肯E-B非线性模型
堆石料的应力变形特性十分复杂,具有显著的非线性和弹塑性等力学特性,已有主流堆石料本构模型从解决实际工程问题需求出发,考虑了主要力学特性和影响因素,力求模型简便易推广[18]。邓肯E-B双曲线模型因能较好地反映堆石料的非线性和压硬性等特点,且模型简单、概念明确,在材料参数确定方面已积累了丰富的经验,因此被坝工界广泛应用。
Konder在土体常规三轴试验基础上,认为主应力差和轴向应变之间可用双曲线表示[19],即:
(1)
式中:σ1和σ3分别为第一和第三主应力,kPa;ε1为第一主应变;a和b为拟合参数。
Duncan在此假设基础上推导了切线模量Et[19],即:
(2)
式中:Et为切线模量,kPa;pa为大气压强,kPa;K、Rf、n、φ、c为试验参数。
体积模量Bt用下式计算[19]:
(3)
式中:Bt为体积模量,kPa;Kb、m为试验参数。
2.2 流变模型
ADINA是国际著名的通用大型有限元软件,自带有丰富的材料本构模型库,特别是在黏弹性本构模型库的基础上建立基于分数阶微积分的流变本构模型,可快速确定模型参数,应用非常方便。ADINA中的流变模型有4种模式,本文选用Law3模型,具体公式如下:
εc=S·T·e-H
(4)
S=a0σa1
(5)
T=ta2+a3ta4+a5ta6
(6)
H=a7/(θ+273.16)
(7)
式中:εc为应变;σ为应力,kPa;t为时间,d;θ为温度,(°);a0、a1、a2、a3、a4、a5、a6和a7均为计算参数。
2.3 计算参数
结合一些工程实例[20]及计算经验,拟定了敏感性分析所需参数。表1和表2分别给出了坝体堆石料E-B模型和Law3流变模型的计算参数。

表1 坝料E-B模型计算参数

表2 坝体材料Law3模型计算参数
3 主、次堆石料分区对大坝变形的影响
3.1 大坝主、次堆石料分区方案
为研究大坝主、次堆石区分界位置对坝体应力变形的影响,本文以200 m高的典型面板堆石坝为例,拟定5种不同的主、次堆石分区方案进行计算比较,如图1所示。方案1~方案5主、次堆石区分界线的坡比依次为1∶0.5、1∶0.2、1∶0.0、1∶-0.2和1∶-0.5。其中正坡比表示分界线偏向于坝轴线下游,负坡比表示分界线偏向于坝轴线上游。对上述5种方案分别建立有限元仿真模型,按竣工期、蓄水期及运行期整理坝体变形和应力成果,并进行比较分析。
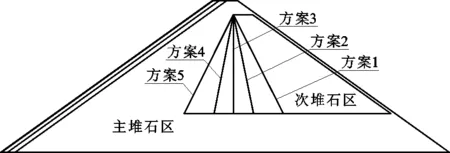
图1 大坝主、次堆石分区方案
3.2 大坝变形特性
通过三维非线性有限元计算,可以得到不同主、次堆石分区方案下大坝的变形及应力分布。限于篇幅,本文仅给出方案1和方案5蓄水期大坝变形分布及运行期(计入流变)大坝变形分布(其他方案大坝变形等值线分布规律与方案1相似),见图2、3,其中水平位移向右为正,竖向位移向下为正。不同方案大坝变形极值变化规律及坝体典型位置沉降流变时程曲线见图4、5。
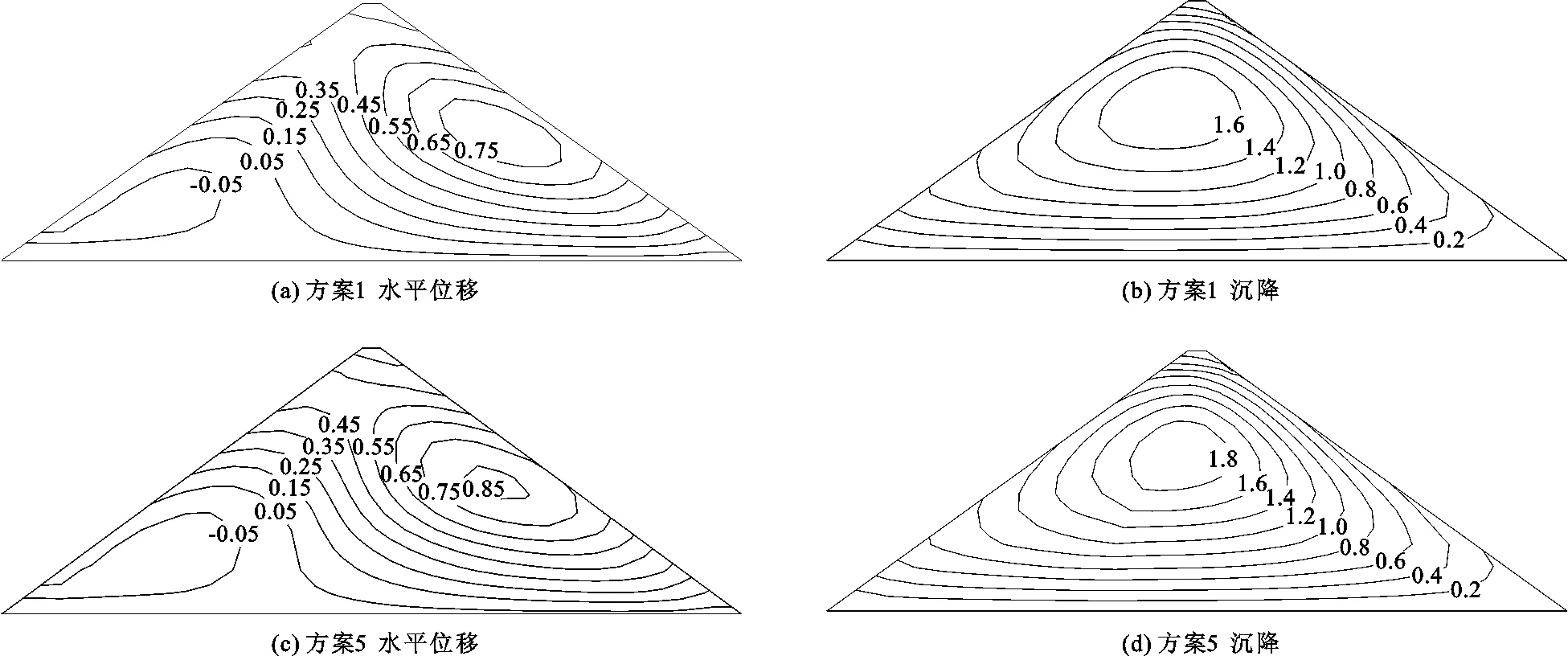
图2 分区方案1和方案5蓄水期坝体变形等值线分布图(单位:m)
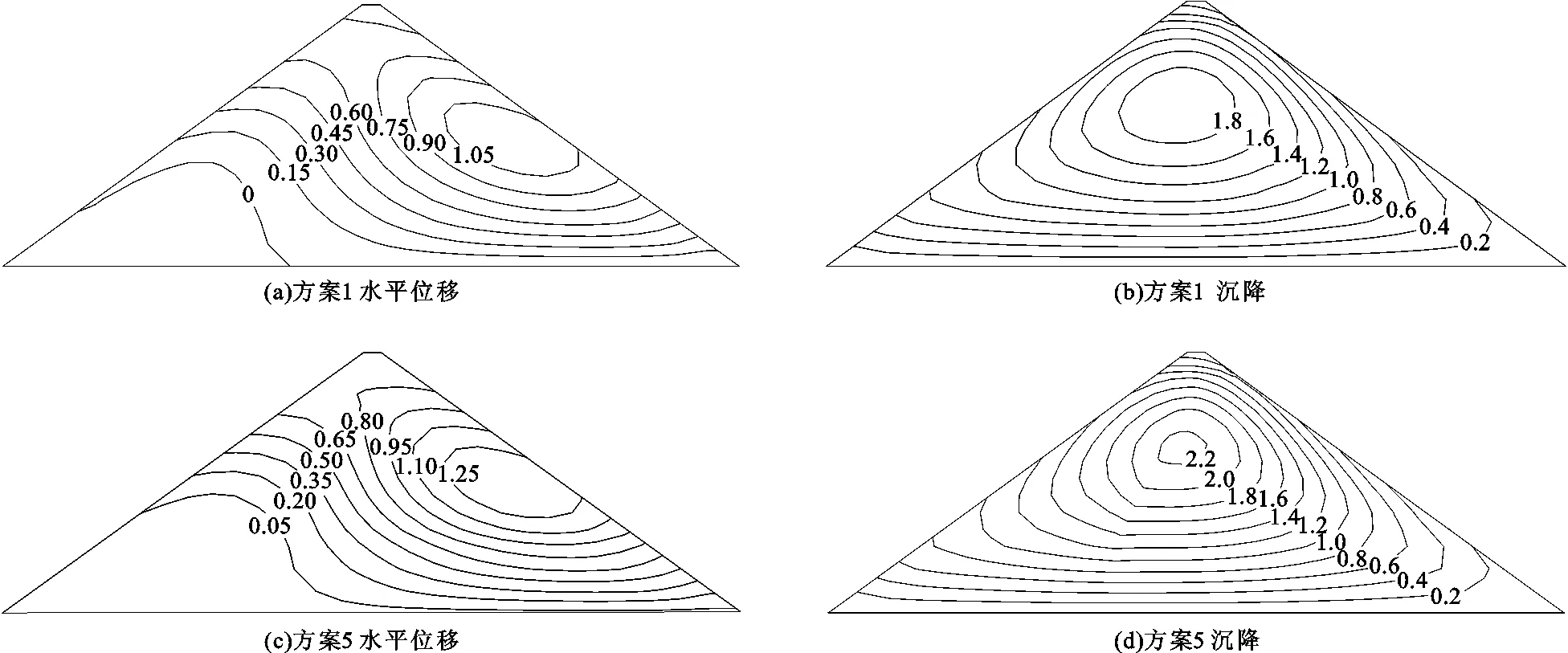
图3 分区方案1和方案5运行期(计入流变)坝体变形等值线分布图(单位:m)
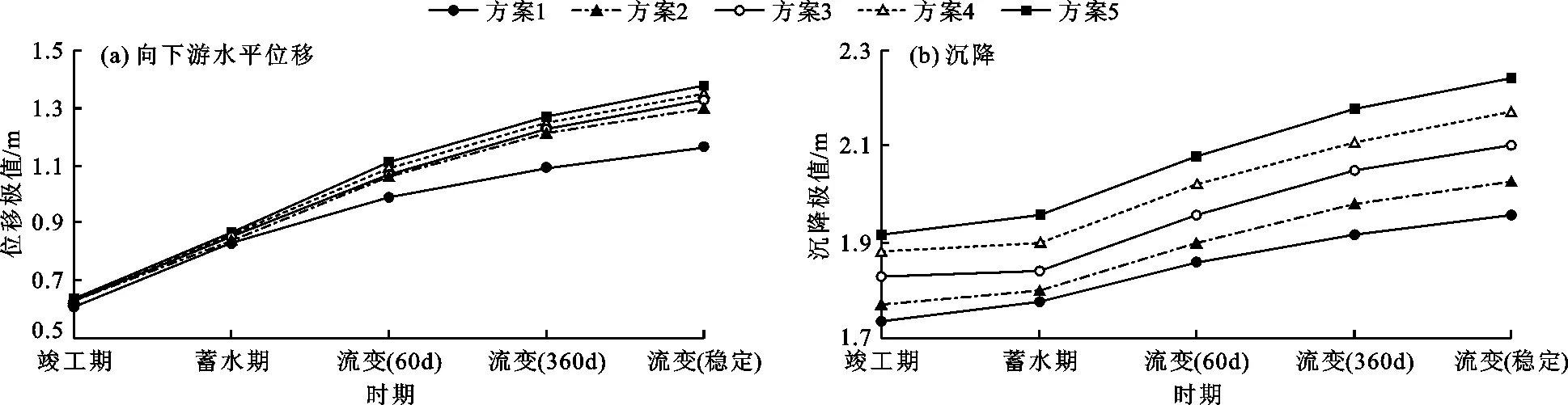
图4 不同分区方案大坝变形极值随工程期变化规律

图5 不同分区方案坝体典型位置沉降流变时程曲线
由图2~5可知:(1)主、次堆石区分界线越向下游倾斜,坝体主堆石区所占比重越大,则坝体沉降量越小。各主、次堆石分区方案下坝体沉降极值最大差别不超10%。坝体沉降极值位置随着主、次堆石区分界线位置向下游倾斜而略向下游移动,坝体最大沉降一般发生在坝轴线略偏向下游堆石区的60%坝高的部位附近。(2)运行期考虑流变后,坝体沉降的极值最大增加了约28 cm,占坝高的0.14%。不同主、次堆石区分界线坡比下,由于主、次堆石区占比不同,堆石体流变效果也有所差别。流变位移变化量随着次堆石区范围的增加而增大,其流变效应也相应增强。
4 主、次堆石料模量比对大坝变形的影响
4.1 计算模型及方案
堆石坝坝料的合理设计对于改善坝体应力与变形,满足坝体稳定性有重要作用。坝体上游部位主要承担着大坝上游面传递来的水荷载,因此坝料的变形模量从上游至下游依次减小。本节仍以上节中200 m高的典型堆石坝为例,进一步考虑主、次堆石模量系数比从0.75∶1到1.5∶1逐渐变化,计算不同方案下大坝应力变形的变化规律。
坝料依然采用E-B模型模拟,流变计算采用Law3模型,计算参数同前。由于坝体沉降量除了与弹性模量相关外,还受体积模量影响,为此选择体积模量系数及指数作为主要变化因子。设主、次堆石的体积模量系数分别为Kb1和Kb2,指数分别为m1和m2(见公式3),则主、次堆石的体积模量比RE为:
(8)
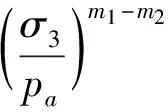
4种敏感性计算方案拟定的参数见表3。

表3 主、次堆石不同体积模量比方案的次堆石料计算参数
4.2 大坝变形特性
图6给出了不同主、次堆石料模量比方案下大坝变形极值变化规律。
由图6可知,不同方案下筑坝材料特性对坝体应力变形性状均有显著影响。不断减小次堆石料的模量,主、次堆石模量比变大,则坝体位移逐渐变大。在方案1中,次堆石模量比主堆石模量大,坝体上游堆石料相对较“软”,故最大沉降位置偏向上游。当次堆石料变“软”后,蓄水期坝体变形明显趋向于下游。水平位移极值由方案I的0.45 m增大到方案Ⅳ的0.75 m。表明下游次堆石区变形对上游坝体有牵制作用。运行期时,考虑流变影响,在减小次堆石料模量情况下,由于堆石料材料“变软”,其流变效应也增强。
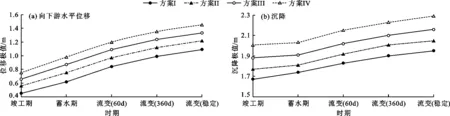
图6 不同主、次堆石料模量比方案下大坝变形极值变化规律
5 结 论
通过对200 m级坝高理想面板堆石坝多方案有限元数值分析比较,得出如下主要结论:
(1)不同主、次堆石区分界对坝体变形分布规律总体影响较小,主、次堆石区分界线倾向下游时,坝体沉降量变小,各主、次堆石分区方案下坝体沉降极值最大差别不超10%。
(2)蓄水期考虑坝体流变后,坝体沉降极值有所增加,最大约占坝高的0.14%。随着次堆石区范围扩大,坝体位移变化量也增大,其流变效应不断增强。
(3)不同方案下筑坝材料特性对坝体应力变形性状有显著影响。不断减小次堆石料的模量,则坝体位移逐渐变大,坝体的沉降极值偏向下游。同时,水平位移极值由方案I的0.45 m上升到方案Ⅳ的0.75 m。表明下游次堆石区变形对上游坝体有牵制作用。
(4)运行期考虑流变影响后,减小次堆石料模量使得坝体流变效应逐渐增强。
