基于PCA-SHO-SVM和PCA-SHO-BP模型的径流预测

李代华

(云南省水文水资源局文山分局，云南 文山 663000)

1 研究背景

探索具有较好预测精度的模型及方法是径流预测研究领域的难点和热点。目前用于径流预测的方法有BP[1-2]、GRNN[3]、Elman[4]、RBF[5]等人工神经网络法以及集对分析法[6]、灰色预测法[7]、支持向量机法[8-10]、投影寻踪回归法[11]、小波分析法[12]、随机森林法[13-14]、组合预测法[15-16]等。上述方法中，由于支持向量机(support vector machine，SVM)和BP神经网络具有较好的逼近能力和预测效果而被广泛应用于径流预测，而如何选取SVM惩罚因子、核函数参数、不敏感系数和BP神经网络权值、阈值成为提高模型预测精度的关键。由于径流序列具有较强的非线性和随机性等多重特性，基于传统或非传统单一预测模型或方法已不能满足径流预测的精度需求。为进一步提高径流预测精度，拓展现有预测模型及方法，本文提出基于主成分分析(principal component analysis，PCA)、斑鬣狗优化(spotted hyena optimizer，SHO)算法与SVM、BP神经网络相融合的径流预测模型，利用PCA对数据进行降维处理，采用SHO算法对SVM惩罚因子、核函数参数、不敏感系数以及BP神经网络权值、阈值进行优化，分别建立PCA-SHO-SVM、PCA-SHO-BP径流预测模型。将PCA-SHO-SVM、PCA-SHO-BP模型应用于云南省龙潭水文站年径流量及枯水期12月月径流量预测，预测结果与利用SHO算法优化但未经降维处理的SHO-SVM和SHO-BP模型、经降维处理但未利用SHO算法优化的PCA-SVM和PCA-BP模型以及未经降维处理也未利用SHO算法优化的SVM和BP模型的预测结果进行对比，旨在检验PCA-SHO-SVM、PCA-SHO-BP模型的预测精度和泛化能力。

2 数据来源与研究方法

2.1 研究区域概况

盘龙河发源于红河州蒙自县三道湾，自西北向东南流注，流经砚山、丘北、文山、马关、西畴、麻栗坡6县，于天保船头注入越南，交泸江汇入红河。盘龙河中越国界以上流域面积6 497 km2，河长247 km，落差1 803 m，平均坡降7.24‰，多年平均水资源量为26.7×108m3，自上而下主要支流有岔河、德厚河、马过河、暮底河、镰刀湾暗河、布都河等。龙潭水文站设立于1951年4月，位于文山城区上游龙潭寨村，集水面积为3 128 km2，观测项目有水位、流量、降雨、蒸发、水温、泥沙，属国家重要水文站和中央报汛站，担负着文山县城重要的防洪报汛任务。

2.2 数据来源与分析

本文以云南省盘龙河龙潭水文站1952-2005年实测水文资料为研究对象，分别利用实测1-10月月平均流量和实测1-11月月平均流量对同年度年径流量和12月月径流量进行预测。经分析，该水文站1-10月月平均流量与年径流量的相关系数分别为0.455、0.441、0.333、0.486、0.497、0.519、0.616、0.822、0.782、0.798，具有较好的相关性；该水文站1-11月月平均流量与12月月径流量的相关系数分别为0.189、0.192、0.220、0.463、0.245、0.180、0.348、0.596、0.511、0.680，最大相关系数仅为0.680，相关性并不十分显著。本文分别选取1-10月、1-11月月平均流量分别作为年径流量和12月月径流量的预报因子，前36 a实测径流量数据作为训练样本，后18 a作为预测样本。

利用SPSS17.0软件对实例数据进行主成分分析降维处理。对于年径流量和月径流量预测的预报因子，前6个特征值累计贡献率分别达93.475%和90.869%，根据累计贡献率大于85%的原则，故选取前6个变量代替原10个和原11个变量进行年径流量和月径流量预测。降维后的数据统计见表1，原始数据限于篇幅从略。

表1 年径流和月径流预测影响因子降维统计表

2.3 PCA-SHO-SVM与PCA-SHO-BP预测模型

(1)

式中：F1为第一主成分;F2为第二主成分，以此类推；n为原变量数；m为新变量数；aij为主成分系数。

2.3.2 斑鬣狗优化(SHO)算法 斑鬣狗优化(spotted hyena optimizer，SHO)算法[18]是Dhiman等于2017年基于斑鬣狗通过群体合作和自身能力进行捕猎行为而提出的一种新颖的启发式算法。算法通过建立数学模型模拟斑鬣狗捕猎过程中的搜索猎物、包围猎物、追捕猎物和攻击猎物4种行为来实现SHO算法获得最优解的目的。根据参考文献[19～21]，SHO数学描述简述如下：

(2)包围猎物。斑鬣狗熟悉目标猎物所处位置，采用包围策略接近猎物。并认定当前最好的斑鬣狗搜索个体位置即为猎物位置。其他斑鬣狗个体会随着猎物移动而不断更新它们当前的位置。利用数学模型表示斑鬣狗包围猎物行为如下：

(2)

(3)

(3)追捕猎物。斑鬣狗通常成群生活和狩猎，并依靠识别猎物所处位置的能力和个体间的信任进行捕猎。利用数学模型表示斑鬣狗追捕猎物行为如下：

(4)

(5)

(6)

(7)

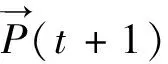
(8)

本文选择径向基核函数作为SVM核函数，径向基核函数表达式为：

K(x,xi)=exp(-g‖x-xi‖2)

(9)

式中：g为支持向量机的核函数参数，g>0。

2.3.4 BP神经网络 设典型3层BP神经网络输入维数为m、隐层为l、输出维数为1，参考相关文献[1]、[2]、[22]，BP神经网络完成映射f:Rm→R1的数学表达式可表示如下：

(10)

(j=1,2,…,p)

式中：lj为隐层到输出层的连接权值；bj为隐层节点的输出；ε为输出层的阈值。采用Sigmoid函数的隐层节点输出表示如下：

式中：ωij为输入层至隐层的连接权值；θj为隐层节点的阈值。

2.3.5 预测实现步骤

Step 1：利用SPSS17.0对实例原始数据进行降维处理，按序列长度2∶1划分训练样本和预测样本，将处理后的数据分别作为SHO-SVM、SHO-BP模型的样本数据进行输入训练。

Step 2：利用训练样本与实测值均方误差构建待优化适应度目标函数，如函数式(12)所示。

(12)

Step 3：设置斑鬣狗群体规模N，最大迭代次数T和算法终止条件。初始化斑鬣狗种群位置Pi和SHO 算法参数h、B、E。

Step 4：计算每个斑鬣狗搜索个体适应度值。

Step 6：检查是否有任何斑鬣狗个体超出给定搜索空间的边界并进行调整。

3 结果与分析

依据前文建立PCA-SHO-SVM、PCA-SHO-BP、SHO-SVM、SHO-BP、PCA-SVM、PCA-BP、SVM、BP模型对实例年径流量和月径流量进行训练及预测。并通过平均相对误差MRE(%)、平均绝对误差MAE(m3/s)和最大相对误差REmax(%)对8种模型的年径流量和月径流量预测结果进行评价，结果见表2，训练-预测相对误差效果图见图1。

模型参数设置为：SVM模型惩罚因子C、核函数参数g、不敏感系数ε搜索范围∈[2-10,210]，交叉验证折数V=5；BP神经网络隐含层节点数通过输入层节点数的2倍减1确定，隐含层传递函数采用logsig，输出层传递函数采用purelin，训练函数采用traingdx，期望误差0.000 1，最大训练轮回设置500次，搜索空间∈[-1,1]。SHO算法参数设置同上。

分析表2及图1可以得出以下结论：

图1 8种模型预测的年径流量和月径流量相对误差

表2 不同模型径流测结果及其对比

(1)从平均相对误差MRE结果来看，PCA-SHO-SVM、PCA-SHO-BP模型对实例年径流量预测的MRE分别为2.34%和2.50%，分别较SHO-SVM、SHO-BP、PCA-SVM、PCA-BP、SVM、BP模型的预测精度提高46.0%、45.5%、61.9%、66.4%、67.8%、73.7%和42.3%、41.7%、59.3%、64.1%、65.6%、71.9%；对实例月径流量预测的MRE分别为6.15%和6.08%，分别较SHO-SVM、SHO-BP、PCA-SVM、PCA-BP、SVM、BP模型的预测精度提高15.5%、21.2%、47.4%、48.6%、52.1%、56.6%和16.5%、22.1%、48.0%、49.2%、52.6%、57.1%。从平均绝对误差MAE结果来看，PCA-SHO-SVM、PCA-SHO-BP模型对实例年径流量预测的MAE分别为0.511和0.535 m3/s，分别较SHO-SVM、SHO-BP、PCA-SVM、PCA-BP、SVM、BP模型的预测结果减小0.381、0.486、0.725、1.021、0.980、1.457 m3/s和0.357、0.462、0.701、0.997、0.956、1.433 m3/s；对实例月径流量预测的MAE分别为1.035和1.006 m3/s，分别较SHO-SVM、SHO-BP、PCA-SVM、PCA-BP、SVM、BP模型的预测结果减小0.148、0.215、0.691、0.898、0.770、1.240 m3/s和0.177、0.244、0.720、0.927、0.799、1.269 m3/s；表明PCA能对大量原始数据进行有效的降维处理，SHO算法能有效优化SVM惩罚因子、核函数参数、不敏感系数以及BP神经网络权值、阈值，PCA-SHO-SVM、PCA-SHO-BP模型用于径流量预测是可行和有效的。

(2)从年径流和月径流预测结果来看，SHO-SVM、SHO-BP模型的拟合、预测精度要远优于SVM、BP模型，表明采用SHO算法优化SVM关键参数以及BP神经网络权值、阈值能有效提高SVM、BP模型预测精度和泛化能力；PCA-SVM、PCA-BP模型的拟合、预测精度同样优于SVM、BP模型，表明PCA能对径流预测影响因子原始数据进行有效降维，主成分变量能够反映原始变量的大部分信息，使SVM、BP模型的预测精度得到进一步提高。

(3)从SHO-SVM、SHO-BP模型与PCA-SVM、PCA-BP模型的拟合、预测效果来看，采用SHO算法优化SVM、BP相关参数对SVM、BP模型的预测精度提升要大于经降维处理的SVM、BP模型。

4 结 论

本文建立了基于PCA-SHO-SVM、PCA-SHO-BP算法的径流量预测模型，并通过实例年径流量和月径流量预测对PCA-SHO-SVM、PCA-SHO-BP模型的预测效果进行验证。结果证明，PCA-SHO-SVM、PCA-SHO-BP模型具有较强的预测精度和泛化能力。并得出以下主要结论：

(1)PCA-SHO-SVM、PCA-SHO-BP模型对实例年径流量和月径流量的预测效果优于SHO-SVM、SHO-BP、PCA-SVM、PCA-BP、SVM、BP模型，表明PCA能对大量原始数据进行有效的降维处理，SHO算法能有效优化SVM惩罚因子、核函数参数、不敏感系数以及BP神经网络权值、阈值，PCA-SHO-SVM、PCA-SHO-BP模型用于径流预测是可行和有效的，PCA-SHO-SVM、PCA-SHO-BP模型均具有较好的预测精度和泛化能力。

(2)采用SHO算法优化SVM、BP相关参数以及利用PCA方法对径流量预测影响因子原始数据进行降维，能有效提高SVM、BP模型的预测精度和泛化能力。相对而言，采用SHO算法优化SVM、BP相关参数对SVM、BP模型的预测精度提升要大于经降维处理的SVM、BP模型。