斜截面浅覆盖层钢栈桥桩基础双向承载结构分析
2021-04-23郭振东黄志强赵国栋张文韬
郭振东,黄志强,赵国栋,4,张文韬
(1.中交瑞通建筑工程有限公司,北京 100084;2.中交路桥建设有限公司,北京 100084;3.沈阳工业大学 建筑与土木工程学院,辽宁 沈阳 110870;4.山东济华燃气有限公司,山东 济南 250000;5.中交路桥北方工程有限公司,北京 100084)
1 研究背景
随着我国桥梁建设的快速发展,在深水区域中,出于对结构施工和环境保护等方面的考虑,需要搭设水上临时施工钢栈桥,作为高速公路主桥和匝道桥施工的主通道、钻孔平台和墩侧作业平台,实现水下作业向陆上作业的转换,待工程完工后拆除。我国南方地区河流多湍急且河床横向坡度较大,水流冲刷作用强烈导致河床多为浅覆盖层或裸岩层。传统的钢管桩振沉工艺无法达到嵌岩深度及承载力的要求,这不仅影响了钢栈桥的施工进度,并且存在很大的安全隐患。为了保证栈桥的安全质量与顺利施工,采用钢管桩钻芯内嵌工字钢并浇筑混凝土的施工工艺,形成钢-混凝土复合桩基础。
斜截面浅覆盖层上的桥梁桩基将同时承受上部结构传递的竖向荷载与流水冲击产生的水平荷载,结构受力较平地桩基而言更为复杂[1-2]。目前,国内外有关斜截面浅覆盖层复合桩基础的系统研究较少,钢栈桥桩基础力学性状、结构特征及各部分的相互作用等方面的研究方兴未艾。赵明华等[1]通过现场试验得到岩质边坡滑坡推力分布规律,建立了关于边坡滑坡体推力的数值分析模型,并提出了适用于斜截面桩基础的内力与位移计算公式;尹平保等[3]通过不同坡度及水平荷载作用角度下斜截面桩基础室内模型试验,测得了桩顶荷载位移曲线及桩身弯矩分布,提出了桩基础水平极限承载力拟合公式;牛富生等[4]通过不同竖向荷载工况下某黄土斜截面桩基进行试验,测得了桩身两侧不同坡面的轴力、桩侧摩阻力及桩侧土压力的分布规律与力学特征,并提出了桩侧摩阻力折减系数;丁选明等[5]、杨磊[6]通过模拟斜桩在不同倾角下的承载特性,得到了桩身倾角与单桩极限承载力、桩身弯矩、桩身轴力及桩身侧摩阻力的变化规律;喻豪俊等[7]通过碎石土斜截面水平受荷桩的数值模拟与现场试验的对比,探讨了不同坡度下桩身变形、弯矩及土压力的变化,提出了单桩水平临界荷载和极限荷载在不同坡度区间内取值时的折减系数。以上研究成果大多考虑单一荷载对桥梁桩基础的影响,并未考虑组合荷载的相互作用,与斜截面浅覆盖层复合桩基础的受力状况有一定差别。
为此,本文结合广东清西大桥临时钢栈桥工程项目,通过现场试验与数值模拟比较,对双向承载的斜截面浅覆盖层钢栈桥桩基础进行研究分析,可为相应工程提供借鉴。
2 现场试验概况
2.1 工程概况
广东清西大桥临时钢栈桥标准段宽度为6 m,跨度为12 m,栈桥桩基础采用双排2根Φ630 mm钢管桩作为支撑,横向间距为4.5 m,并通过槽钢连接,安置平联与剪刀撑,在桩顶两侧焊接牛腿。钢管桩往上依次安置工字钢承重梁、贝雷主梁、工字钢分配梁(间距0.75 m)、倒扣槽钢作为桥面板(间距0.25 m),其结构如图1(a)所示。钢管桩嵌固深度为0.2 m,内部钻探取芯,嵌入I10工字钢作为锚杆,内嵌深度为5.2 m,并浇筑C30水下混凝土,浇筑高度为3 m,最后形成钢-混凝土复合桩基础,如图1(b)所示。
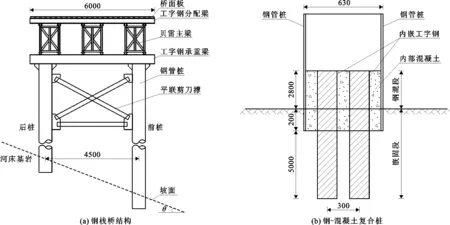
图1 实例工程钢栈桥结构及钢-混凝土复合桩结构示意图(单位:mm)
钢栈桥施工现场多为横向坡度较大的浅覆盖层区,河床底基岩主要以强风化砂岩、碎裂岩为主,承载力特征值为300~450 kPa,侧摩阻力特征值为80~120 kPa,覆盖层淤泥厚度不足1 m,坡度比为1∶2.6,部分桥段位于裸岩区,且水流湍急多漩涡,平均径流深为1.47 m,最大流速为3.5 m/s。
2.2 试验设计
现场试验为准静载试验[8],采用总重为500 kN(车重+荷重)的12 m3混凝土罐车,左车轮位于第2贝雷片与第3贝雷片间,右车轮位于第4贝雷片与第5贝雷片间,以0.5 km/h速度匀速通过第1~第5跨,每1.5 m静止20 s。试验现场如图2所示。

图2 试验现场示意图 图3 应变测点布置图
在钢管桩桩顶布置拉杆式直线位移传感器,记录桩顶竖向与水平位移;在钢管外壁每隔2 m环形布置4个应变片(共4×11=44片),如图3(a)所示;在内嵌工字钢翼缘、腹板每隔1 m布置6个应变片(共6×5=30片),如图3(b)所示。由IMC数据采集系统自动采集试验全过程数据,待试验结束后进行数据分析。
2.3 试验结果
(1)桩顶位移。斜截面浅覆盖层钢栈桥钢-混凝土复合桩的竖向荷载与桩顶位移关系曲线如图4所示。其中水平位移方向为顺桥方向。
由图4可知,对于斜截面浅覆盖层钢-混凝土复合桩,当竖向荷载在0~300 kN时,桩顶竖向与水平位移基本呈线性增加关系,且增加速率较小;当竖向荷载超过300 kN时,桩顶位移曲线呈指数增加关系,桩顶竖向与水平位移均迅速增加。其中,前桩的竖向与水平位移均大于后桩,且柱顶竖向位移约为桩顶水平位移的2倍。当竖向荷载为500 kN时,前桩与后桩的最大竖向位移分别为38.32、36.41 mm;最大水平位移分别为19.82、19.12 mm,两者相对位移差均小于为2 mm,桥面未出现明显的倾斜。
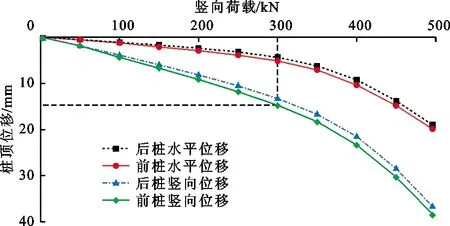
图4 钢-混凝土复合桩竖向荷载-桩顶位移曲线
可见,竖向荷载对斜截面浅覆盖层钢-混凝土复合桩的竖向和水平位移均产生了影响。以本文现场试验为例,为了限制钢栈桥桩基础竖向与水平位移,需要将竖向荷载限制在一定范围内(小于300 kN),而当竖向荷载超过一定范围时(大于300 kN),对水平位移的抑制作用已不明显,且竖向位移显著增加。并且随着竖向荷载的增加,前桩与后桩的相对竖向位移幅度增大,而相对水平位移保持在较小的范围内,因此,在工程设计中应综合考虑因竖向荷载过大引起的桥面倾斜。
(2)桩身应变。由于钢-混凝土复合桩前桩与后桩的现场试验应变值差异较小,因此取两者的平均值,分别得到钢-混凝土复合桩外钢管应变和桩内工字钢应变随行车时间的变化曲线,如图5所示,当车辆行驶150 s时,刚好处于测试桩中心位置。
由图5(a)可看出,随着测试车辆由远至近,钢管的压应变先是逐渐增大,当车辆达到测试桩位置时,应变达到最大压应变,当车辆远离时,应变逐渐变小,并恢复到车辆来临之前的状态。
由图5(b)可看出,内嵌工字钢的应变也是呈现这种先增大后减小的变化。表明桩的整体应变变化处于弹性状态,满足设计承载要求,且能很好地传递水平方向的荷载。
桩体中间嵌入的工字钢起到了桩加固效果,增加了桩的嵌固能力,且组成复合桩桩体的工字钢、钢管以及中间灌注的混凝土三者共同承载,协调变形,整体呈现受压状态,变形连续,体现了内部混凝土粘结良好,工字钢整体处于弹性范围内,弹性变形良好。车辆经过瞬间,外钢管顶部与嵌固处最大应变值分别为533.12×10-6、243.54×10-6(图5(a)),这对外钢管的疲劳寿命具有影响,应在钢栈桥使用过程中,加强对外钢管的相关监测。
从图5(b)中的数据同样看出,钢混段中部的工字钢压应变较小,但随着桥面荷载的临近,连接钢混段与嵌固段的工字钢应变迅速增大,最大接近了36×10-6,大于其他部位的工字钢应变变化量,工字钢底部应变值最大为6.56×10-6,顶部应变值最大为4.24×10-6,分析表明钢混段与嵌固段交界处内嵌工字钢出现应变集中现象,这部分是混凝土与岩石交接处,受力不均匀,主要承受了行车荷载对桩体的竖向和水平作用力以及流水冲击力。嵌固段中部的桩身变形主要体现了桩底土层承载能力的影响,嵌固段工字钢受力不大,起主要受力作用的是钢混段,说明可以考虑将原设计的嵌固段5.2 m的设计长度适当减少。
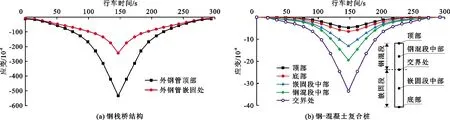
图5 钢-混凝土复合桩外钢管和桩内工字钢应变随行车时间的变化曲线
3 数值模拟
3.1 模型参数选取
为了便于建立模型,提高运算效率,选取一跨钢栈桥进行建模研究。根据设计资料,钢栈桥标准段宽度为6 m,跨度为12 m。对于钢-混凝土复合桩而言,外钢管均为Φ630 mm×8 mm钢管,其中前桩长22 m,后桩长20.25 m,嵌固深度为0.2 m,内部混凝土浇筑高度为3 m,内嵌工字钢为I10,嵌固深度为5.2 m。根据圣维南原理[9],竖向荷载只对一定范围内的土体产生明显的影响,计算土体尺寸采用钢-混凝土复合桩间距长宽的5倍,即计算的横向范围为60 m,纵向范围为22.5 m,因为斜截面浅覆盖层,不考虑淤泥层的影响,中心垂直范围取为16.5 m,坡度比为1∶2.6。
钢材均为Q235B,采用二次塑流本构模型[10];内部混凝土为C30,采用圆钢管混凝土本构模型[10];计算土体主要以强风化砂岩、碎裂岩为主,采用Mohr-Coulomnb本构模型[11-12]。网格以六面体为主,均为实体单元,提高内嵌工字钢的网格密度,如图6所示,以便观察内嵌工字钢的力学变化。斜截面浅覆盖层钢栈桥桩基础模型如图7所示。

图6 钢-混凝土复合桩模型

图7 斜截面浅覆盖层钢栈桥桩基础模型
在数值模拟中,应当合理地考虑钢混界面的粘结效应以提高模型的计算精度,但目前为止,对钢混界面的粘结效应的相关研究不足,缺乏相关的本构关系。部分研究表明[13-14],在未考虑钢混界面的粘结效应的情况下,数值模拟的结果依然可以满足计算的要求,并提高了运算效率。因此,为了便于数值模拟,本文在建立斜截面浅覆盖层钢栈桥桩基础模型时,没有考虑钢混界面的粘结效应,在接触部分直接用绑定约束来模拟钢混之间的相互作用。
对于单跨钢栈桥而言,需要考虑相邻钢栈桥的影响。分别对单跨钢栈桥顶部某方向施加集中力F,得到相应的侧移值Δ,即可得到弹性刚度k=F/Δ。通过上述方法计算,得到钢栈桥沿两个方向的弹性刚度。在斜截面浅覆盖层钢栈桥模型中将以上计算所得弹性刚度的弹簧施加于钢栈桥,即认为考虑了相邻钢栈桥的影响。为了与现场实际情况保持一致,将模型桩周土及钢-混凝土复合桩外钢管底端的边界节点施加X、Y、Z3个方向的0位移约束。
3.2 模型加载及合理性验算
为了保证模型验证的准确性,在施加荷载之前,首先设置地应力平衡[15],然后在桥面板中心上部建立了参考点,在参考点与桥面板之间建立了刚体约束,并以集中力的形式向基准点施加轴向荷载,分10级加载(每级100 kN),直至1 000 kN。在钢管桩顺桥向施加流水荷载Fw[16]。水位取20年一遇最高水位19.37 m,流水荷载Fw为:
(1)
式中:Fw为流水荷载,kN;γ为水的重度,取9.80 kN/m3;v为设计流速,取3.50 m/s;A为复合桩阻水面积,取3.78 m2;g为重力加速度,取9.80 m/s2;K为桥桩系数,取0.8,可得Fw=18.52 kN。流水压力合力的着力点,假定在设计水位线以下0.3倍水深处。
为了比较数值模型与现场试验的拟合程度,选取前桩的竖向荷载-桩顶竖向位移曲线为评价依据,比较曲线如图8所示。
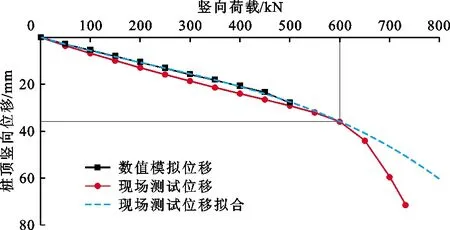
图8 竖向荷载-桩顶竖向位移比较曲线
由图8可得,数值模型与现场试验虽然不是完全的吻合,但大体数值和曲线趋势仍具有良好的一致性,数值模拟与现场试验的位移值相对误差基本小于8%,平均值为4.2%,满足计算要求。与现场试验值相比,数值模拟值普遍较高。分析的原因可能是:(1)在模拟过程中,桥面处于理想的均布应力状态,存在理想的铰约束;而在实际试验中,桥面处于铰与固定约束之间,不存在理想的铰约束,因此对钢栈桥的承载力有一定的影响;(2)在模拟中,忽略了内嵌工字钢与外钢管、内部混凝土之间的相对滑移,直接在内嵌工字钢与外钢管、内部混凝土之间施加约束,与复合桩的实际受力情况不同,使钢栈桥承载力偏高;(3)由于模拟时各材料均是各向匀质,而实际情况中钢栈桥在施工安装过程中难以保证材料各向同性匀质,最终导致钢栈桥位移数值模拟值与现场试验值相比偏大。
由图8还可看出,当竖向荷载加载至600 kN时,钢栈桥竖向位移数值模拟曲线出现拐点,取该级荷载作为钢栈桥桩基础极限承载力,此时钢栈桥桩基础位移云图如图9所示。

图9 钢栈桥桩基础位移云图 图10 外钢管应力云图 图11 内嵌工字钢应力云图
现场试验竖向位移曲线在竖向荷载为500 kN终止,没有出现拐点,因此运用多项式拟合推测后期曲线走势,经计算可得出,当竖向荷载为613 kN时,现场试验竖向位移曲线将会出现拐点,推测结果和数值模拟较为吻合,证明本模型所选参数与简化方式合理,可以进行下一步的数值模拟分析。
4 现场试验和数值模拟对比分析
4.1 钢-混凝土复合桩基础应力对比
竖向荷载为500 kN时,钢-混凝土复合桩外钢管及内嵌工字钢的应力云图分别如图10、11所示。由图10、11可看出,外钢管在顶部及嵌固处应力较大,内嵌工字钢在钢混段与嵌固段交界处出现应力集中现象,前桩受到斜截面浅覆盖层的影响更大。
将钢-混凝土复合桩外钢管和内嵌工字钢不同位置的现场试验应力值与数值模拟值进行对比,结果如表1所示。
由表1可知,各位置应力的数值计算值与现场试验值相差较小,钢-混凝土复合桩能较好地传递荷载,使外钢管、内部混凝土和内嵌工字钢三者协同受力,内嵌工字钢在交界处出现应力集中,但未到达屈服,满足承载能力要求。
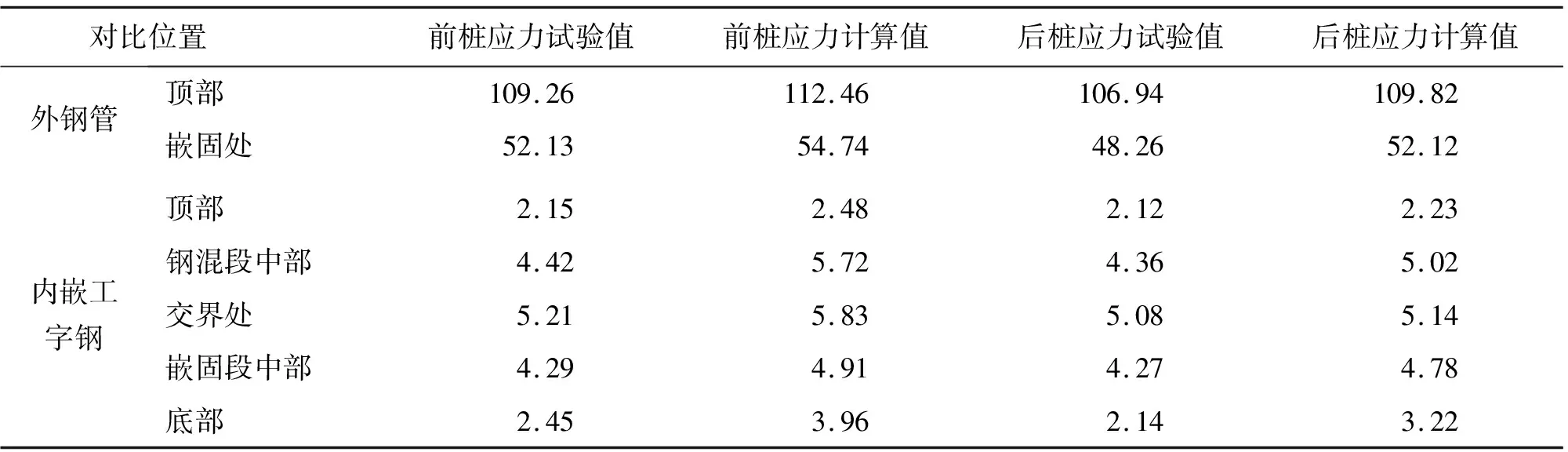
表1 钢-混凝土复合桩不同位置的现场试验应力值与数值模拟值对比 MPa
4.2 钢-混凝土复合桩基础弯矩对比
竖向荷载为500 kN时,钢-混凝土复合桩的桩身弯矩分布曲线如图12所示。
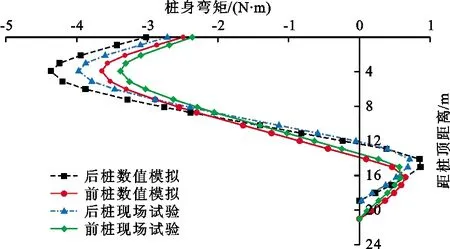
图12 钢-混凝土复合桩的桩身弯矩分布曲线
对图12进行分析如下:
(1)在双向荷载的作用下,现场试验与数值模拟的桩身弯矩分布曲线均呈“S”型分布,前桩与后桩桩身分别在距桩顶14与12 m附近出现反弯点[17]。在流水冲击与竖向荷载的双向作用下,导致复合桩桩顶会产生流水方向的水平位移,从而产生桩顶截面弯矩[18]。桩底边界条件为嵌固,因此桩底截面无弯矩产生。
(2)桩身上段均存在较大负弯矩,前桩与后桩的最大负弯矩值均出现在距桩顶4 m左右处,前桩现场试验与数值模拟的最大弯矩值分别为3.38、3.64 N·m,后桩的最大弯矩值分别为3.97、4.39 N·m,后桩比前桩的弯矩增幅分别为17.5%、20.6%,说明对于斜截面浅覆盖层钢-混凝土复合桩,桩顶弯矩荷载会对桩身弯矩最大值产生影响,且对于后桩的影响更加明显。
(3)由于钢管桩嵌固深度不足且受到流水的冲击作用,在桩身中部产生了水平方向的弯曲变形,即使桩顶的竖向荷载可以抵消、抑制部分桩身弯曲变形,但桩身也不可避免地会产生附加弯矩[19-20],对于钢-混凝土复合桩而言,因内部浇筑混凝土并嵌入工字钢,从而提高了桩体整体强度和刚度,有利于钢栈桥的稳定。
5 结 论
本文通过实例工程的现场试验与数值模拟,对双向承载的斜截面浅覆盖层钢栈桥桩基础进行研究分析,主要得到以下结论:
(1)在斜截面浅覆盖层区,钢栈桥承受竖向荷载与水平流水荷载,前桩桩顶的竖向与水平位移均大于后桩。随着竖向荷载的增加,桩顶竖向位移增幅加剧,而桩顶水平位移增幅相对较小,桩顶竖向位移约为桩顶水平位移的2倍。当竖向荷载大于300 kN时,对桩顶水平位移的抑制作用已不明显,且桩顶竖向位移显著增加。
(2)在现场试验过程中,外钢管与内嵌工字钢各部位均为压应变,且前桩应变值均大于后桩。当竖向荷载大于300 kN时,外钢管顶部应变值迅速增加,但并没有出现明显变形,钢管桩处于弹性应变范围内,内嵌工字钢在钢混段与嵌固段交界处出现应变集中现象。
(3)对于钢-混凝土复合桩而言,桩体中间嵌入的工字钢起到了桩加固效果,增加了桩的嵌固能力,且组成复合桩桩体的工字钢、钢管以及中间灌注的混凝土三者共同承载,协调变形,达到了预想的设计效果。
(4)现场试验与数值模拟的桩身弯矩分布曲线均呈“S”型分布,桩身上段均存在较大负弯矩,由于流水荷载的作用,使得桩顶弯矩对桩身弯矩最大值产生影响,且对于后桩的影响更加明显。竖向荷载虽能在一定程度上抑制桩身变形,但仍会产生附加弯矩。内嵌工字钢可提高桩体强度和刚度,有利于钢栈桥的稳定。
