巴塘水电站导流洞平面闸门流激振动试验研究

2021-04-23李文胜王延召吴敏睿盛传明徐国宾

水资源与水工程学报 2021年1期

刘昉，李文胜，王延召，吴敏睿，盛传明，徐国宾

(天津大学水利工程仿真与安全国家重点实验室，天津 300350)

1 研究背景

闸门挡水时，在水流脉动压力作用下常常发生振动，结构振动与其固有特性和外部激励荷载密切相关，而剧烈的闸门振动会对枢纽工程的安全稳定运行造成严重影响[1-3]。闸门因剧烈振动而无法正常工作的实例屡见不鲜，轻则会对闸门自身材料造成疲劳损伤，重则会导致结构发生动力失稳而破坏[4]，如刘家峡平面工作闸门振动应力超出设计容许应力、四川狮子滩水电站定轮工作门在运行时发生剧烈垂向振动、西津电站船闸输水廊道上闸首的平面定轮工作门由于闸门振动导致定轮悬臂轮止轴板剪断、轮子脱落。所以，研究闸门振动问题具有重要的现实意义，一直是水利工程中的重点研究课题[5-6]。通过比较水流脉动频率与结构自振频率，进行共振校核，作为判断闸门结构设计参数选择优劣的标准[7-8]。为进一步明确闸门的振动情况，通常采用水弹性模型试验或数值计算手段进行分析，对闸门流激振动响应进行预测，规范和指导闸门的运行方式，确保结构振动处于安全范围内[9-12]。明确闸门的振动问题是保证水工钢闸门安全运行的重要环节，研究闸门结构在水动力载荷作用下的动力稳定性及安全性等问题具有重要意义[13-15]。

目前国内外研究闸门振动的方法主要是制作弹性相似模型进行试验，通过测算闸门结构振动时附近的水力特性，判断闸门是否会出现较为危险的共振行为。为研究巴塘水电站导流洞平面闸门局开泄流过程中的闸门振动问题，本文利用完全水弹性物理模型进行模拟试验，比较了门体上水流脉动频率和闸门自振频率，并对闸门结构进行应变测试，探究运行时的闸门结构振动和变形特征。通过水弹性试验对闸门流激振动响应进行预测，期望为闸门结构优化设计提供技术指导[16-18]。

2 模型建立

2.1 工程概况

巴塘水利枢纽工程以发电为主，正常蓄水位初拟为2 545 m，死水位为2 541 m。图1给出了该工程导流洞进口段纵剖面图，其中进口底板高程为2 487.0 m，洞身长796.03 m，进口引渠长30.0 m，导流洞洞身段断面型式为城门洞型，断面尺寸为12 m×14 m(宽×高)，平面闸门型式为潜孔平面闸门，闸门尺寸为7.8 m×14.2 m(宽×高)。进水塔孔口按2孔设计，单孔口尺寸为6 m×14 m(宽×高)。进水塔闸室段长18 m，宽24 m，塔高48 m，塔后设25 m长渐变段，由方型洞渐变为城门洞型，隧洞底坡i=5.02 ‰。在原型中，工作闸门为平面闸门，其门叶结构主要材质为Q345钢，弹性模量E=200 GPa，泊松比μ=0.3，钢结构密度为ρ=7.85×103kg/m3。平面闸门运行速度为1.5 m/min，梁格中布置铅皮进行配重，确保闸门能够动水闭门。门体采用滑块支承方式，配合单吊点6 300 kN固定卷扬机进行启闭操作。

图1 巴塘水利枢纽工程导流洞进口段纵剖面图(单位：m)

2.2 物理模型试验方法及测点布置

模型按重力相似准则进行设计，整体模型模拟范围为导流洞进水口至导流洞中段，为敞口泄流条件。整个模型由引水口(水箱内)、闸室段、渐变段、有压洞段、尾水渠5部分组成。表1给出了各物理量的模型比尺参数。

表1 各物理量模型比尺参数

闸门模型试验研究分为两个阶段，第1阶段为平面闸门动水压力模型试验，该模型采用有机玻璃制作而成，其目的为满足糙率相似以及便于观察闸下和导流洞内的水流流态，主要测量闸门结构所受的时均水压力和脉动水压力，闸门模型如图2(a)所示。第2阶段为平面闸门流激振动试验研究，该模型中闸门采用完全水弹性材料制作，模型严格满足结构弹性相似和水力学相似。本试验所采用的水弹性模型材料按照水弹性相似率的要求研制，用来模拟门叶结构的刚度及变形，所选模型材料的密度为7.8×103kg/m3，模型的综合动摩擦系数f为0.26～0.30，模型如图2(b)所示。

在模型门体上、下游和底缘位置共布置了8个压力测点。压力传感器测量范围为-4～30 kPa，分辨率为0.01 kPa，误差≤±0.3% F.S.(满量程)，自振频率大于300 Hz。通过中国水利水电科学研究院研制的DJ800多功能监测仪采集系统，测量闸门门体上的动水压力。此外，在平面闸门水弹性相似模型的主横梁翼缘板及主纵梁翼缘板等主要构件上共布置15个动应力测点(BFH120-5AA-X30型电阻应变计)及在门顶上布置3个电压型加速度传感器(测量范围为10 m/s2；灵敏度为0.5 V/ms-2；分辨率为5×10-5m/s2)。各测点的布置位置如图2(c)所示。通过动态电阻应变仪和北京东方振动和噪声技术研究所研制的DASP智能采集系统配合恒流供电器进行闸门应变加速度的采集。

图2 闸门模型及监测点群布置

在模型试验中，闸门模型的启闭速度由电机控制，启闭速度在0～1.5 m/min范围内调节。同时将闸门顶部水平向振动加速度测点J2、闸门上部中间纵梁动应变测点Y15和闸门底缘处脉动压力测点D4作为评估闸门振动、应变和水流脉动压力等参量变化特性的典型测点。

3 试验结果分析

3.1 水动力荷载

作用在闸门门体上的水压力可分为脉动压力和时均压力[19]，通过分析时域、幅值特征和频域能量分布特性等，可以获得水流的脉动特性。利用模型试验测得不同工况下作用在闸门上的局部脉动水压力，本文将平面闸门底缘处测点D4作为脉动水压力典型测点，着力分析闸门底缘区域水流脉动压力的变化特征。模型试验工况主要包括3种运行水头和5种闸门局开条件，其中运行水头分别为14、13和12 m，闸门相对开度分别是0.09、0.1、0.2、0.3以及0.5。图3给出了各运行水头下测点D4的脉动压力与闸门相对开度的关系；图4给出了运行水头为14 m时，测点D4的压力时程线及经FFT变换后的功率谱密度曲线。由图3、4可知，底缘区域的水流脉动压力随闸门开度的增大而减小，随运行水头的升高而增大；闸门时均压力分布规律较好，水流脉动能量的主频较低且分布于1 Hz以下，脉动能量频率集中于10 Hz以内。

图3 各运行水头下测点D4脉动压力与闸门相对开度的关系

图4 测点D4压力时程线及其功率谱密度曲线(运行水头14 m)

3.2 动应力响应分析

试验观测表明，各测点动应力响应均方差值在0.1 MPa以内。保持上游水位稳定时，闸门在小开度区域动应力的均方差值相对较大，运行水头由12 m升高至14 m时，闸门动应力均方差在0.02～0.08 MPa之间，脉动应力均方差最大为0.08 MPa，表明上游水头在运行期内变化时，对闸门动应力响应影响较小。若按6倍均方差计算应力幅值为0.48 MPa，脉动应力较小。闸门结构受力特征良好，其刚度和强度均满足设计要求，闸门可平稳、安全运行。运行水头为14 m、闸门在不同相对开度运行时，各动应力测点的测量结果见表2。

表2 运行水头14 m闸门不同相对开度各测点动应力均方差测量结果 MPa

闸门由全开至全关过程中，门体上部典型测点Y15的应力时域过程线如图5所示，在不同运行水头下，门体上部典型测点Y15的时均应力与闸门相对开度关系曲线如图6所示。由图5、6可知，在闸门关闭的全过程中，门体振动比较平稳，相同运行水头下门体典型测点Y15应力基本不随闸门开度的变化而变化；测点Y15时均应力随运行水位的升高而增大，闸门不同开度下门体典型测点Y15的应力值最大为11.32 MPa(运行水位为14 m)，闸门承受的动应力较小，满足动应力不大于材料允许应力20%的要求[20]。

图5 闸门关闭过程中典型测点Y15的应力时域过程线图6 典型测点Y15的时均应力与闸门相对开度关系曲线

3.3 加速度及位移响应分析

平面闸门在运行水头为14 m局部开启运行时，门体顶部典型测点J2的加速度均方差值以及将加速度信号经过二次积分得到的振动位移均方差值如表3所示。

由表3可知，不同闸门开度下门体3个方向振动加速度均方差均在0.060 m/s2以内，振动位移均方差值在35 μm以内。试验观测表明，上游水头由12 m升高至14 m时，测点J2的加速度均方差最大值由0.015 m/s2增大到0.058 m/s2，各点加速度(水平向、垂向、侧向)均方差量级相当，最大为0.058 m/s2，按3倍均方差计算加速度幅值约为0.174 m/s2；位移均方差由0.393 μm增大到30.658 μm；按3倍均方差计算最大位移幅值约为91.974 μm。依据美国阿肯色河通航枢纽中心提出的按振动位移均方差值划分水工钢闸门振动强弱的标准[20]，位移均方差值为0～0.050 8 mm的振动对结构的影响可以忽略不计；位移均方差值在0.050 8～0.254 0 mm之间的振动为微小振动；位移均方差值在0.254 0～0.508 0 mm之间的振动为中等振动，位移均方差值大于0.508 0 mm的振动为严重振动。因此，该导流洞平面闸门在局部开启挡水时的振动属于微小振动。

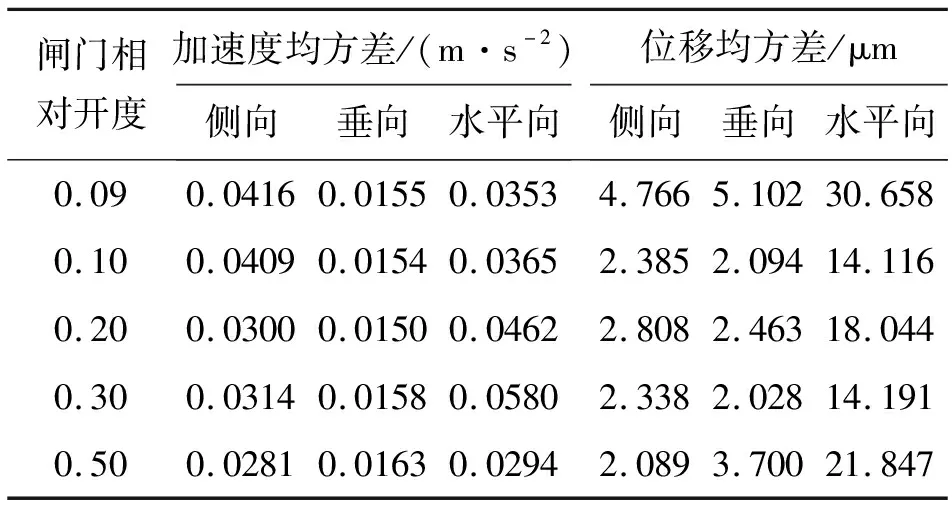
表3 运行水头14 m闸门不同相对开度典型测点J2的加速度均方差和位移均方差

图7为运行水头14 m时，门体顶部典型测点J2不同方向的加速度均方差与闸门相对开度的关系曲线。在闸门关闭过程中门体下落较为平稳，闸门在各相对开度运行时的各测点振动加速度值较小。由图7可看出，3个方向的加速度响应中，水平向振动加速度均方差值相对较大，侧向次之，垂向最小；随着闸门开度逐渐增大，门体侧向振动响应逐渐减小，垂向振动响应先减小后略有增大，水平向振动响应先增大后减小，在闸门相对开度为0.3时达到最大，其后有所减小[21]。

图7 典型测点J2不同方向的加速度均方差与闸门相对开度关系曲线(H=14 m)

图8为运行水头14 m、闸门相对开度为0.3时，由傅里叶变换得出的典型测点J2水平向加速度时程线和功率谱密度曲线。由图8可知，闸门主要的振动能量集中在1.0 Hz之内，主频为0～0.4 Hz，与水流脉动频率基本一致。因此，闸门结构振动表现为水流脉动荷载作用下的低频受迫振动。通过时域积分，可由实测加速度过程得到闸门振动位移的变化过程，其结果表明，闸门振动位移稳定，主频为0.19 Hz，能量主要集中在1.0 Hz以内。

图8 典型测点J2水平向加速度时程线及其功率谱密度曲线(运行水头14 m，闸门相对开度为0.3)

4 闸门模态分析

通过ANSYS Workbench 平台对平面闸门进行结构模态分析[22-23]。在计算干模态时，闸门和钢丝绳分别采用壳单元(Shell63)和杆单元(Beam188)进行模拟；在湿模态分析中，闸门上、下游水体采用ANSYS单元库中的三维流体声单元(Fluid3D)模拟[24-25]；流固耦合分析时，闸门的主横梁、主纵梁及面板等主要结构用实体单元(SOLID45)进行模拟。上游顺水流方向水体长度取20 m，下游顺水流方向水体长度取6 m。上游静水压力作用明显，故顺水流向只在滑块承压处施加位移约束，同时在闸门底槛施加位移约束。闸门是由6 300 kN固定卷扬式启闭机配合拉杆完成动水起闭，钢丝绳直径在50～ 80 mm范围内选取，弹性模量E=(1.05～1.15)×105MPa，所以钢丝绳用竖向力杆单元模拟。受拉杆的作用，在吊绳吊点处施加全约束，以便获得平面闸门的频率和振型。数值计算得出的平面闸门相对开度为0.09的情况下，前4阶自振频率和振型如表4所示，其中干湿模态1阶振型特征见图9。