吸入式扫路车轴承耦合故障振动特性分析

肖俊洲

长沙中联重科环境产业有限公司 湖南长沙 410000

环境保护意识的提升，使人们对社会生存环境的要求越来越高，传统的人工扫路工具已被吸入式智能扫路车代替，由于此种扫路车可实现对道路垃圾的自动化清扫，且使用成本较低、工作效率较高，因此吸入式扫路车一经投放市场后，便受到了多个产业对其的争先追捧。

目前，扫路车也因此被广泛应用于市场，但由于此种装置的研发尚处于初期阶段，在使用中仍可能存在不可避免的问题[1]。以轴承为例，此种零部件是属于机械设备中的关键构成部分，主要用于支撑机械旋转体在运行或工作过程中的摩擦系数，是吸入式扫路车的关键构成零件。但根据市场统计数据显示，超过45%的吸入式扫路车故障均是由于轴承故障所导致的，当扫路车轴承发生故障时，装备内其它相关零构件的正常运行也受到相同的影响，即发生耦合故障，会直接对扫路车的正常运行造成影响[2]。在进行故障点诊断过程中，故障处会产生振动信号，并通过复杂的路径将信号传输至振动传感器，以此为依据，用于定位耦合故障发生点，但考虑到振动信号的传输会受到路径中多因素的影响，这些因素都会造成终端对故障点识别的不准确。因此，本文将以吸入式扫路车为例，对其轴承发生耦合故障时的振动特性展开分析，以此提高对耦合故障发生点定位的精准度。

1 吸入式扫路车轴承耦合故障振动特性分析

1.1 构建吸入式扫路车轴承传动非线性动力模型

由于吸入式扫路车轴承耦合故障振动问题具有明显的非线性动力学特征，因此，在对其进行特性分析时，需要构建吸入式扫路车轴承传动非线性动力模型。首先，利用6自由度Timoshenko梁结构对吸入式扫路车轴承中的主动轴结构、从动轴结构进行建模；其次，结合Jones轴承建立理论，构建吸入式扫路车轴承在模拟静力状态下的动力学模型结构，以此进一步推导出吸入式扫路车轴承结构的刚度矩阵[3]。最后，结合有限元分析模式，针对吸入式扫路车轴承转子耦合的非线性动力学模型进行构建。按照上述构建思路，对吸入式扫路车轴承的弹性转轴进行模型构建，沿着轴承的轴线，将其划分为若干个相同大小的轴段结构，如图1所示。

图1 吸入式扫路车轴承传动非线性动力模型

图1 中每个吸入式扫路车轴承轴段均采用两节点的Timoshenko 梁结构模型，并保证其每个节点上均含有三个不同方向上的移动，并分别对应相应的转动自由度θ 。结合拉格朗日算法，得出吸入式扫路车轴承传动的动力学方程，如公式（1）所示：

公式（1）中，eQ 表示为吸入式扫路车轴承弹性轴段所承受的广义力矢量； eM 表示为轴承传动单元质量矩阵； eG 表示为轴承传动矩阵； eK 表示为轴承传动单元刚度矩阵。吸入式扫路车轴承在高速旋转的过程中，会受到外载荷的作用影响，因此轴承结构的内圈、外圈。球心等位置均会发生相应的变化[4]。结合Jones轴承结构模型构建理论，得出吸入式扫路车轴承受力变形后其内部几何关系。

考虑到吸入式扫路车轴承的离心力、轴承力矩、惯性力等特点，构建在任意受载条件下的静力学分析模型。在静力学分析模型当中，将吸入式扫路车所有轴承的内圈结构之间的接触力进行叠加计算，并始终保持其承载力的平衡，确定吸入式扫路车轴承的非线性接触力矩。

1.2 轴承耦合故障转子裂纹呼吸效应分析

当吸入式扫路车轴承出现耦合故障问题时，通常会伴随着轴承转子结构的裂纹现象产生，因此在对其故障振动特性分析时，还需要对轴承耦合故障转子裂纹进行呼吸效应分析[5]。假设轴承转子总长度为L，则轴承转子所承受的轴向上的力与剪力、扭矩、弯矩之间会形成恒定的外力作用。假设每个节点上均包含6个自由度，根据公式（2）计算得出轴承耦合故障转子裂纹引起的附加柔度系数为：

公式（2）中，γ 表示为轴承耦合故障转子裂纹引起的附加柔度系数；α 表示为转子转动角度；jp 表示为恒定外力；ip表示为轴向力；U 表示为轴承耦合故障转子裂纹左端距离。根据上述公式计算，结合断裂力学能量释放理论得出，当吸入式扫路车发生轴承耦合故障时，转子产生的裂纹会引起一定的附加应变能，裂纹从出现到逐渐扩展所需的能量可通过不同裂纹结构对应的应力强度因子以及泊松比计算得出[6]。再通过由于无裂纹产生的转子的柔性系数矩阵进行比较，可以最终得出出现裂纹的转子刚度矩阵。

为保证后续对吸入式扫路车轴承耦合故障振动特性进行分析时，得到更加准确的结果。本文引入应力强度因子理念，用于模拟吸入式扫路车轴承出现耦合故障问题时产生裂纹的呼吸效应[7]。当转子裂纹处于张开的状态时，则认为此时的受力为拉应力，假设应力强度因子为T，则此时T的取值为T>0；当轴承转子结构的裂纹处于闭合状态下，则认为此时的受力为压应力，T的取值为：T<0；当轴承转子结构的裂纹处于闭合与张开的节点时，T的取值为：T=0。综上所述，在吸入式扫路车轴承发生耦合故障时，得出裂纹闭合与张开相互垂直的直线，并将其作为临界线，结合公式（2）计算得出，转子裂纹的柔性系数以及积分的上下界线[8]。

若在分析过程中，吸入式扫路车轴承转子的裂纹处于其他状态时，则应当通过裂纹的开闭临界线确定其上下积分界限。确定的具体步骤为：

首先，沿吸入式扫路车轴承转子裂纹的边界，将其划分为多个大小完全相同的组成部分；

其次，随着轴承转子的不断运动，在吸入式扫路车不同的运动状态下，分别计算得出，其故障裂纹边界的应力强度；

最后，将总应力归零，再次确定裂纹闭合和张开的边界点，并将其代入到上述公式（2）计算得出故障时裂纹的张开和闭合状态的上下界限。

2 实验分析

2.1 轴承齿轮转子耦合故障稳态响应动力学特征分析

以轴承在发生耦合故障问题时，其转子结构的裂纹相对深度为0.5mm为例，其裂纹的刚度系数应当在两个转动周期内幅值应当以波浪型的趋势发生改变。根据上述“呼吸效应”进一步得出，裂纹的产生可看作是两种周期成分的组成：幅值波动较大的长周期和幅值波动较小的短周期[9]。根据吸入式扫路车轴承的转动形式，假设发生耦合故障问题时，轴承转子裂纹位于主动轮转轴位置，为方便后续论述，假设裂纹的单元长度L为75mm，裂纹单元的直径d为25mm，则按照上述建模方式，构建吸入式扫路车轴承传动非线性动力模型。其它齿轮的参数如表1所示。

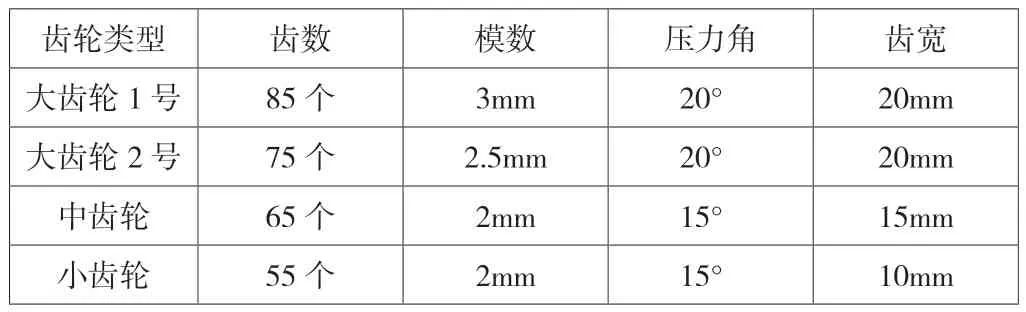
表1 吸入式扫路车轴承传动非线性动力模型齿轮参数

结合本文上述论述，结合数值积分算法，对存在转子裂纹现象的轴承耦合故障振动问题进行动力学分析。当吸入式扫路车的轴承齿轮传动过程中，若存在轴承转子裂纹产生，则此时的信号时域将成为故障最明显的特点，同时还会伴随着赋值调制的现象产生。当载波与调制波之间产生了不用转动频率或拟合频率时，其变化幅度更加明显，此时产生的现象证明，吸入式扫路车轴承耦合故障振动时，在啮合频率位置上产生了较为明显的边频带。

针对上述现象进行分析得出，其主要原因是转子裂纹呼吸效应造成的。除此之外，轴承中转子结构产生裂纹的是还会伴有呼吸效应的产生，又会进一步造成转子的刚度系数出现呈波形周期性的变化。在两种不同频率的作用下，相互耦合叠加还会造成刚度系数的动态激励源产生。除此之外，吸入式扫路车轴承齿轮自身的激励源也会产生时变刚度啮合，导致啮合频率的振动现象产生。因此，在上述多种不同动态激励的作用下，最终产生了幅值调制的振动响应。

当吸入式扫路车轴承单轴转子发生裂纹耦合故障现象时，其响应与频率当中会出现更加明显的频成分，这一特征可视为吸入式扫路车轴承发生耦合故障的重要征兆。针对吸入式扫路车轴承转子发生多种齿轮共同作用的耦合效应时，通常会表现出与单轴转子完全不同的故障特征。因此，在对吸入式扫路车轴承耦合现象进行故障诊断时，应当通过二倍频、幅值调制等特点，综合判断吸入式扫路车轴承是否存在转子裂纹故障现象产生。

2.2 轴承齿轮转子耦合故障瞬态响应动力学特征分析

轴承齿轮转子耦合故障稳态响应动力学特征外，吸入式扫路车轴承在发生耦合故障时，还会产生相应的瞬态响应动力学特征。而通常情况下，轴承中齿轮的耦合故障中含有较为丰富的状态信息，而通过稳态响应很难对其发生的具体故障问题在瞬态下体现[10]。因此，在对轴承齿轮转子耦合故障瞬态响应动力学特征分析时，首先假设吸入式扫路车轴承转频在15s时间内由0Hz逐渐增加到50Hz。通过将含有轴承转子耦合故障的齿轮传动瞬态响应与正常轴承转子的瞬态响应进行对比得出，未发生耦合故障问题的正常齿轮其转子的第一个共振峰值应当出现在3.2s-3.5s范围内，而含有转子耦合故障的齿轮，其第一个共振峰值出现时间为2.45s。将瞬态响应时的加速信号进行短时傅里叶变换，通过对比得出，正常齿轮转子的第一个共振峰值出现时，其频率大小为683.4Hz，而含有转子耦合故障的齿轮，其第一个共振峰值出现时，频率大小为523.85Hz，明显小于正常齿轮。产生这一现象的主要原因是轴承转子在发生耦合故障问题时，轴承的固有频率减小。因此，综上所述，当吸入式扫路车轴承发生耦合故障问题时，其固有频率的减小与信号的转频的提升，可作为判断轴承转子结构是否存在裂纹现象的重要因素。

3 结语

为探究吸入式扫路车轴承在发生耦合故障时具备的振动特性，结合Timoshenko 梁结构模型构建理论，以某吸入式扫路车为例，开展研究。通过本文研究得出，通过稳态响应中的二倍频、幅值调制以及瞬态相应中的频率的减小与信号的转频的提升，均可以作为判断轴承中转子结构是否处在断裂的主要判定依据，以此在发生轴承耦合故障问题时，可以进一步为其维护与维修提供依据，从而在第一时间恢复吸入式扫路车的正常运行。在后续的研究中，为保证吸入式扫路车的稳定运行，还将对其发生耦合故障的条件因素进行深入分析，从而在出现耦合前，避免故障问题的产生。