宽带相控阵天线孔径对SAR 成像影响研究

王 文，张 俊

（西安电子工程研究所，陕西西安 710100）

0 引言

现代战场环境对于雷达的功能提出了更高要求，需要其既能搜索、跟踪目标，又能进行合成孔径雷达（Synthetic Aperture Radar，SAR）成像。SAR 成像作为一种微波的主动遥感手段，具有获取地表图像的能力，自20 世纪50 年代被提出以来，便受到雷达和遥感领域专家的广泛关注并取得快速发展［1-4］。它是一种新型的雷达体制［5］，合成孔径雷达作为一种高分辨率雷达，原理是通过发射大带宽的脉冲信号获得高的距离分辨率，利用载机运动形成的合成孔径提高横向分辨率，得到目标的二维图像［6］。

传统雷达天线多采用抛物面天线，随着电控移相器、开关和收发组件的出现及发展，相控阵天线渐渐取代了抛物面天线［7-8］。相控阵天线的孔径由大量相同阵元（例如裂缝、偶极子或贴片）组成，每个阵元可实现相位和幅度的独立控制。其具有波束指向灵活、目标容量大、系统可靠性高、对复杂目标环境适应能力强等优势［9-10］。它满足了现代雷达对于多功能的需求，成为现代雷达发展趋势［11］。

SAR 成像是现代雷达最重要的功能之一，在相控阵天线上实现SAR 成像功能成为重要研究课题［12］。天线形式的改变会对合成孔径雷达成像算法造成影响，当成像分辨率较低时，这种影响不是很明显。但随着雷达技术的发展，为实现距离向的高分辨率，常采用上百兆赫兹带宽的线性调频信号，如TecSAR 卫星的最大信号带宽大于200MHz［13］。合成孔径雷达成像算法对于回波信号的建模往往忽略了天线的孔径，将其看作一个点，算法在该模型基础上可以进行很好的成像，但是对于相控阵天线而言，这种信号模型的描述则不准确。相控阵天线由一个个独立的阵元构成，每个阵元都可以独立接收回波信号，由于阵元在空间中所处位置存在差异，这会使得每个阵元到场景中心的斜距相较于成像算法中的场景中心距存在微小的斜距误差。若单纯地将各阵元的回波信号叠加，就会存在误差，给成像结果带来影响。因此，基于相控阵天线建立精确的回波信号模型，并分析其对SAR 成像算法的影响，成为SAR 功能在相控阵天线雷达上进行工程实现的关键。

1 相关工作

对于相控阵天线的波束形成控制，常用方式有光纤延迟线和数字移相器两种方式，光纤延迟线效果好，可以对频带内的信号附加群时延，但成本较高，占用空间较大；数字移相器是对传输信号额外附加相位，由于带内是固定相位，对宽带信号进行处理时会引入一些误差，但是由于其成本低、占用空间小，仍是机载、星载SAR 系统主要采用的方式。关于采用数字移相器的相控阵雷达对SAR 成像的影响，国内外学者对此进行了研究，并取得系列成果。Teitelbaum［14］通过频域均衡的方式实现了宽带通道均衡，通过傅里叶变换方法算出各通道均衡滤波器的期望频率响应，再通过最小二乘法进行逼近。Luison 等［15］研究了相控阵天线阵元采取非周期式排列对SAR 成像的影响，通过非周期的布阵方式，可使在阵元间距大于半波长的同时有效扼制栅瓣的产生；撒文彬等［16］研究了相控阵天线发射信号的频率对于天线方向图的影响，随着发射信号频率的改变，会影响天线对于不同方向接受回波的增益，在回波信号引入关于幅度的调制。但上述研究忽略了天线孔径大小对于不同阵元到场景中心斜距的影响；翁元龙等［17］通过分析直接数字频率合成器波形产生原理，给出在其基础上固有的调频斜率计算方法，但由于现代雷达的SAR 成像功能大多具有多种模式、量程和分辨率，因此该方法具有一定局限性。

以上方法都未将相控阵天线的孔径大小作为SAR 成像结果的影响因素。本文通过理论分析和实验仿真相结合的方式，从回波信号的源头入手，不再将天线视为一个点，而是将相控阵天线孔径大小作为变量，对相控阵雷达接收到的回波信号进行研究，改进了成像算法中的回波信号模型；再在该信号模型基础上，对其进行部分相位补偿，而后进行信号的相干叠加，分析信号模型改变带来的包络走动和相位误差对于成像结果的影响，得出理论分析结论，并通过仿真实验验证理论分析的准确性；最后采用常用雷达参数，对仿真实验成像结果的图像质量进行定量分析，得到不同参数下分辨率、主瓣展宽及峰值旁瓣比等图像质量指标的恶化情况，对合成孔径雷达成像功能在相控阵天线上的工程实现具有一定借鉴意义。

2 合成孔径雷达回波信号模型

合成孔径雷达通过发射宽带线性调频信号实现距离向的高分辨率，通过平台运动形成的虚拟阵列实现方位向的高分辨率。假设载机平台与成像区域的关系如图1 所示，载机平台以速度v 沿X 轴方向运动，Z 轴方向背离地球中心，hz代表平台高度，φ为俯仰角，Rt为平台到目标点P 的实时斜距，是慢时间t 的函数。

Fig.1 The geometric relationship between the carrier platform and the imaging scene图1 载机平台与成像场景几何关系

雷达发射的线性调频信号：

其中，τ为快时间，fc为发射信号载频，Tp为发射信号脉宽，γ为调频率。

单一点目标的回波信号解调至基带后，其表达式为：

其中，t为方位慢时间，Ta为方位孔径时间。

由图1 所示的几何关系可以得到：

目标点到平台的实时斜距Rt与慢时间t 呈双曲线关系，在小斜视角的条件下，可以在vt=0 处进行泰勒展开，并对高阶项进行忽略处理，得到其近似的抛物线结果。

将式（4）代入式（2）可以得到回波信号的表达式为：

式（5）中第一包络项为回波在方位向的包络，第二包络项与第一相位项共同构成了回波信号的距离向信息，经距离向脉冲压缩处理后，会在R0+(vt)2/2R0处形成sinc 型的距离包络。第二相位项为常量，可以不用考虑。第三相位项对应回波的方位向信息，该相位为具有线性调频特性的方位向频率调制。以距离—多普勒成像算法为例，该算法采用插值方式进行距离徙动（Range Cell Migration，RCM）矫正，使得回波能量在距离向集中到R0，再对其进行方位脉冲压缩，使得回波能量在方位向集中，形成二维sinc 型的包络，完成成像。

3 相控阵天线雷达回波模型建立及误差分析

3.1 回波信号模型建立

成像算法在建立回波信号模型时忽略了雷达天线的尺寸，将其看作一个点，这种假设在使用抛物面天线，或者SAR 系统分辨率低时是可以接受的。但对于宽带相控阵天线，由于其具有很高的距离分辨能力，使得相控阵天线上不同阵元与目标之间的斜距误差不能忽略，因此需要对回波信号模型进行修正。

考虑一个多通道SAR 系统配备了具有M 个阵元的相控阵天线，其阵元位置沿方位向均匀分布，如图2 所示。假设所有通道和目标位于三维笛卡尔坐标系，由于飞行姿态的原因，载机的机头指向与其运动方向存在一个偏流角θ，相控阵天线需要根据偏流角θ的变化，实时调整天线的电波束指向，使其垂直于载机运动轨迹，实现条带SAR 的正侧视成像。与之相对应的，相控阵天线的阵面指向与其电波束指向也存在一个斜视角θ，顺时针为正。在实际情况中，该角度随慢时间t而变化，对于固定翼等平稳的平台，其关系多为一个缓变的、低次的函数，而对于旋翼等高震动平台，函数中的高次分量会大大增加。d为相邻阵元的间距，对于一个相控阵天线，阵元间距d为定值。Rt为天线中心阵元到目标点P的实时斜距，是慢时间t的函数，R(t,m,θ,d)是第m个阵元到目标点P的实时斜距，它是与慢时间t、阵元通道号m，阵元间距d和天线斜视角θ有关的函数。因此，有第m通道在t时刻的坐标为(vt+mdcosθ,mdsinθ,hz)，-M/2 ≤m≤M/2，则由平面几何关系可得：

同样对其进行抛物线近似处理，得到结果。

Fig.2 3D geometry diagram of phased array antenna SAR system图2 相控阵天线SAR 系统3D 几何示意图

式（7）中R(t,m,θ,d)是对于式（2）中Rt在相控阵天线条件下更为精确的描述，将式（7）代入式（2），得到进行阵元斜距修正后的回波信号模型。

式（8）中第一包络项不变。第二包络项和第一相位项相较于式（5），该包络和相位是通道数m，阵元间距d和天线斜视角θ的函数，即距离向存在包络走动现象。包络走动会使得成像算法中的RCM 矫正出现问题，同一目标的回波能量无法很好地矫正到同一距离单元，对后续方位向的处理造成影响。

对比式（8）和式（5）的第二相位项，可以看到相控阵的回波信号中该项不再是常量，引入一个相位误差，对于同一采样点，不同阵元间的阵元间距d和斜视角θ是相同的，通道号m的不同会使得不同阵元收到的回波信号无法进行相干叠加，故必须将其相对于参考阵元进行相位补偿。

第三相位项相较于式（5），当斜视角θ为不为0 的定值时，多普勒中心发生变化，这会导致方位脉冲压缩时产生的sinc 型包络发生位置偏移。当斜视角θ随慢时间t 变化时，回波信号的线性调频特征会被破坏，会导致方位脉压结果变差，出现主瓣展宽、旁瓣提高等现象。

综上分析，相控阵天线回波信号模型与SAR 成像算法中的回波信号模型，主要差异体现在由于相控阵天线不同阵元在空间中的位置存在差异，使得其到场景中心的斜距与成像算法中的场景中心距存在斜距误差，该误差在距离向上产生包络走动，对RCM 的矫正带来问题。而且，由于斜距误差的存在，斜距变化产生的多普勒频率也会出现误差。

3.2 成像结果理论分析

为了消除多通道回波信号第二相位项出现的误差对接收信号相干叠加的影响，相控阵天线在接收回波信号时，会通过移相器对每个阵元附加一个相位，该相位为：

对每个阵元接收的回波进行相位修正，再对全部阵元进行相干叠加，并进行一定的近似处理，则接收信号为：

可以看出，相比普通天线接收的回波信号，经过相位补偿之后的相控阵天线接收信号是M 个具有不同距离向的包络位置与多普勒中心回波的叠加。经距离向脉冲压缩处理后，会以斜距对应的距离单元为中心形成sinc 形的尖峰，由于不同阵元的斜距不同，处理结果为其叠加结果。在进行成像处理时，需要对回波信号进行RCM 的矫正，即将目标的瞬时斜距Rt≈R0+(vt)2/2R0近似矫正为R0，对于阵列天线的回波信号，经过RCM 矫正处理后，会残留一个斜距误差ΔR(t,m,d,θ)。

对于特定阵元而言，m、d为定值。当θ为定值时，ΔR(t,m,d,θ)为关于慢时间t的一次函数，经过成像算法处理，相比单通道天线成像结果，其尖峰出现的位置距离向会偏移(mdcosθ)2/2R0-mdsinθ，由于其多普勒中心的偏移，尖峰位置在方位向会偏移mdcosθ，当θ为关于慢时间t变化的函数时，由于成像算法无法将其在整个合成孔径时间内的回波能量矫正到同一距离单元，故成像结果得到的尖峰效果会出现不同形式的恶化。ΔR(t,m,d,θ) 中，mdsinθ≫，因此斜距误差中mdsinθ占主导。当斜视角θ与慢时间t成奇次关系时，矫正后的回波能量在距离向分布在多普勒零点所在距离单元的两侧，其成像结果呈现为双边展宽；当斜视角θ与慢时间t成偶数次关系时，校正后的回波能量距离向上分布在多普勒零点的单侧，其成像结果呈现为单边展宽；而当斜视角θ与慢时间t成正弦关系时，则表现为会出现多个多普勒频率的零点，造成成像结果在方位向出现多个能量集中区。

3.3 成像结果仿真验证

对上述理论分析结果进行仿真实验，为使现象明显，仿真中设置的误差值较大。当斜视角θ不随慢时间t变化时，成像结果如图3 所示；当斜视角θ与慢时间t成二次、三次及正弦的变化关系时，成像结果如图4、图5 和图6 所示。

Fig.3 The oblique viewing angle θ has no relationship with the slow time t图3 斜视角θ 与慢时间无关系

Fig.4 The oblique viewing angle θ has a quadratic relationship with the slow time t图4 斜视角θ 与慢时间t 呈二次关系

Fig.5 The oblique viewing angle θ has a cubic relationship with the slow time t图5 斜视角θ 与慢时间t 呈三次关系

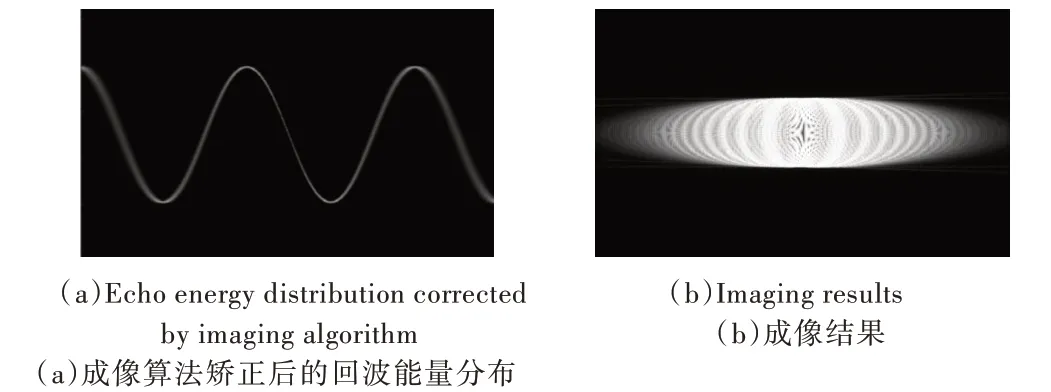
Fig.6 The oblique viewing angle θ of view has a sinusoidal relationship with the slow time t图6 斜视角θ 与慢时间t 呈正弦关系

通过成像结果可以看到，相较于成像算法矫正后回波能量在同一距离单元所形成的点目标的二维sinc 函数成像结果，实验得到成像结果明显恶化，恶化形式与上述理论分析结果一致，验证了理论分析的准确性。

4 仿真实验与结果分析

用仿真实验的方式验证由于相控阵天线阵元间存在间距带来的阵元斜距误差对成像质量的影响，并评估不同参数变化影响图像质量指标恶化程度。设机载平台SAR系统初始参数如下，中心频率为10GHz，信号带宽为480MHz，采样频率为640MHz，阵元间距d=λ/2=1.5cm，正侧视，为优化成像结果，对结果加汉明窗处理。

仿真实验为点目标成像效果仿真实验，阵元数量M 设置100 个和200 个两个对照组，场景中心斜距R0设置20km和50km 两个对照组，天线斜视角θ随着慢时间t设置二次型变化、三次型变化、正弦变化3 个对照组，并对成像结果做方位向剖面处理，对其冲激响应曲线进行图像质量指标测量，量化和评估斜距误差带来的影响。

仿真结果如图7—图12 所示。为使结果具有对比性，将成像结果以M=100 为基准，进行归一化处理。对于上述仿真实验结果进行分析，发现不论场景中心斜距是20km 还是50km，当阵元数量为1 时，点目标的冲激响应函数为理论值。当阵元数量不为1 时，存在阵元斜距误差，成像结果的图像质量与阵元数量M 成反比，阵元数量M 越大，成像结果图像质量越差，随着斜距误差的增大，冲激响应函数畸变加剧，出现主瓣展宽、旁瓣抬高、变形等变化，同时峰值幅值发生变化，主瓣峰值能量降低，回波能量的集中性下降。而且场景中心斜距R0也是影响成像质量的一个重要因素，随着场景中心斜距的减少，阵元斜距误差会变大，其中常数项的增大会使得单个阵元成像结果中心点的偏移量增大，高次项会使得冲激响应函数畸变更加明显。

对冲激响应曲线进行图像质量指标评估结果如表1 所示，表中给出了分辨率、展宽系数和峰值旁瓣比在不同成像条件下定量测量的结果。可以看到，随场景中心斜距的减小，主瓣展宽情况迅速恶化，故在SAR 系统进行近距成像时，需注意阵元间距带来的成像结果恶化。对于峰值旁瓣比指标，正弦关系表现较差，恶化情况达10db 以上，可见多个多普勒零点对于系统指标的影响是剧烈的，在系统设计中应尽量避免。

Fig.7 R0=50km θ ∝t2 azimuth section view图7 R0=50km θ ∝t2 方位向剖面

Fig.8 R0=50km θ ∝t3 azimuth section view图8 R0=50km θ ∝t3 方位向剖面

Fig.9 R0=50km θ ∝sint azimuth section view图9 R0=50km θ ∝sint 方位向剖面

Fig.10 R0=20km θ ∝t2 azimuth section view图10 R0=20km θ ∝t2 方位向剖面

Fig.11 R0=20km θ ∝t3 azimuth section view图11 R0=20km θ ∝t3 方位向剖面

Fig.12 R0=20km θ ∝sint azimuth section view图12 R0=20km θ ∝sint 方位向剖面

Table 1 The influence of envelope walking error on imaging quality index表1 包络走动误差对成像质量指标的影响

5 结语

本文针对宽带相控阵天线孔径对于SAR 成像的影响问题，提出了适用于相控阵天线的回波信号模型，通过研究该模型对成像算法的影响，促进成像算法的工程应用。从误差产生的原因、天线体制改变对SAR 成像算法处理流程的影响、天线体制改变对成像结果的影响这3 方面进行了详细分析及仿真验证。本文提出的由于天线阵元间距带来的位置误差，在现有采用移相器的相控阵天线上还没有较好的解决方法，仅能通过预留足够的指标余量达到指标要求。随着移相器相关技术的发展，实现宽带内的动态移相，方可从根本上消除该误差，从而实现理论和工程的统一。