关注探索性思维的培养

王思俭

摘要：“八省联考”数学卷第20题对学生的空间想象能力和符号抽象能力提出了较高的要求，尤其是考查了学生的探索性思维，包括类比转化、抽象建模、整体思考、归纳猜想、演绎证明等。数学探索性思维是左右脑并用的，兼顾直观与抽象、直觉与逻辑、归纳与演绎、类比与联想等思维方式的。在数学教学（尤其是解题教学）中培养探索性思维，要特别注意：既关注证明，又关注猜想;既关注运算，又关注思考;既关注动脑，又关注动手。

关键词：八省联考;数学卷;曲率问题;探索性思維

一、“八省联考”数学卷第20题及其考情分析

由教育部考试中心统一命制，江苏等八省市高三学生参加的2021年高考模拟演练的数学卷第20题如下：

北京大兴国际机场（如图1）的显著特点之一是各种弯曲空间的运用。刻画空间的弯曲性是几何研究的重要内容。用曲率刻画空间弯曲性，规定：多面体顶点的曲率等于2π与多面体在该点的面角之和的差（多面体的面的内角叫作多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和。例如：正四面体在每个顶点有3个面角，每个面角是π3，所以正四面体在各顶点的曲率为2π-3×π3=π，故其总曲率为4π。

（1）求四棱锥的总曲率;

（2）若多面体满足：顶点数-棱数+面数=2。证明：这类多面体的总曲率是常数。

（一）试题分析

本题以北京大兴国际机场的建设成就为实际应用背景，引入大学微分几何中的曲率概念，仅考查简单多面体的空间结构（如顶点、棱、面之间的数量关系）和平面多边形的内角和，而不涉及常见的平行、垂直和空间向量等的论证与计算，颇有新意。

本题的第一问研究特殊情况，是铺垫性问题，主要考查学生阅读理解和迁移运用的能力。第二问研究一般情况，有一定的难度，其常规解法如下：

设多面体的顶点数为V，棱数为E，面数为F。多面体的总曲率=V×2π-多面体所有面角之和=V×2π-多面体所有面的内角和。

仔细分析常规解法，不难发现，第二问除了考查学生阅读理解和迁移运用的能力，对学生的空间想象能力和符号抽象能力提出了较高的要求，尤其是考查了学生的探索性思维（没有现成的公式、结论可以套用），包括类比转化（如将所有面角之和转化为所有面的内角和、将多边形转化为三角形）、抽象建模（一般化表示顶点数、棱数、面数以及各个面的边数）、整体思考（建立有关量的关系，如所有面的内角和与面数、各个面的边数的关系，总边数与棱数的关系）、归纳猜想（从特殊到一般）、演绎证明（代入消元、计算化简）等，可见其构思精巧。

（二）考情分析

此题江苏全省均分大约1分，而我校在没有讲评的前提下，限时15分钟，让学生再做一次，结果均分也只有2.56分。

分析错因，可以发现：（1）部分学生没有读懂新定义的“曲率”和“总曲率”，没有建立总曲率与各顶点的面角之和总和，即多面体的所有面角之和的关系;（2）部分学生缺乏转化能力（也可能缺乏整体思维），没有理清所有面角之和与所有面的内角和的关系;（3）部分学生缺乏符号抽象能力（也可能缺乏空间想象能力），只研究了棱锥和棱柱这两类符合题意的特殊多面体的总曲率，或者不能适当地表示有关的量;（4）部分学生缺乏整体思维（纠缠于局部），或缺乏由特殊到一般的思维（不能继续利用特殊多面体展开探索），不能建立所有面的内角和与面数、各个面的边数的关系，或不能建立总边数与棱数的关系;（5）部分学生推理和运算能力不过关。归根结底，主要还是探索性思维能力不足。

二、教学启示

教育部考试中心研制的《中国高考评价体系》强调：“高考命题，应有一定数量的探究性问题，适度增加试题的思维量，考查思维方法。”上述试题跳出了常见的知识考点，充分体现了对探索性思维的考查。

徐利治先生认为，数学探索性思维是左右脑并用的，兼顾直观与抽象、直觉与逻辑、归纳与演绎、类比与联想等思维方式的。因此，在数学教学（尤其是解题教学）中培养探索性思维，要特别注意以下几点：

（一）既关注证明，又关注猜想

左右脑并用的数学探索性思维，往往集中表现为猜想与证明的有机统一。在解题教学中，教师不能就题论题，而要引导学生类比发散、归纳推广，猜想更多的结论，并尝试给出证明，从而既调动学生的积极性，又培养学生思维的灵活性、批判性。

【案例1】 一道数列题的教学片段

（教师出示例1，学生尝试解决。）

师很好！用斜率解题时一定要考虑斜率不存在的情况。思路清晰，运算简洁，通性通法，过程严谨。由此可以看出，选择不同的直线方程会产生不同的运算量。在解题过程中，要学会回顾总结，积累解题经验，才能提高解题能力。

（三）既关注动脑，又关注动手

通常认为，数学是思维的科学，是符号化（抽象）的形式科学。但实际上，数学同时具有科学的实验（观察、操作）特征，也是体验化（具象）的内容科学。从关注单纯的动脑到关注综合的动脑与动手（包括运用其他感官），也是探索性思维的重要特征之一。因此，教师不仅要引导学生动脑思考，还要让学生动手实验，探索解决问题的思路，同时也能提升操作能力和想象能力。

【案例3】 一道立体几何题的教学片段

（教师出示例3。）

例3（1）给出两块相同的正三角形纸片（如图3、图4），要求用其中一块剪拼成一个正三棱锥模型，另一块剪拼成一个正三棱柱模型，使它们的全面积都与原三角形的面积相等。请设计一种剪拼方案，分别用虚线标示在图3、图4中，并做简要说明;

（2）试比较你剪拼的正三棱锥与正三棱柱的体积的大小;

（3）如果给出的是一块任意三角形的纸片（如图5），要求剪拼成一个直三棱柱模型，使它的全面积与原三角形的面积相等。请设计一种剪拼方案，用虚线标示在图5中，并做简要说明。

师怎样由正三角形剪拼成正三棱锥？

生正三棱锥的底面是正三角形，三个侧面是全等的三角形，因此，要剪出一个正三角形和三个全等的三角形。

师你是怎样剪的？

生沿着某一个角剪出一个正三角形;将余下的图形，剪成三个全等的三角形即可，需要尝试。

师那么，这个正三角形的边长是多少？侧面三角形的边长与它有什么关系？你考虑了吗？

（该生思考。另一位学生回答——）

生（出示图6）由于侧面三角形的一条边就是底面正三角形的边，折叠起来后有的边要重合为侧棱，因此，取三边中点连线，这样就分割成四个全等的正三角形，沿虚线折起就构成正三棱锥——实际上是正四面体。

师很好！其实正四面体沿侧棱剪开铺平就是正三角形，这就是三维图形与二维图形的互相转化，即降维与升维。再来看怎样由正三角形剪拼成正三棱柱。

生根据正三棱柱的特点，需要两个正三角形作为底面，类似正三棱锥的剪拼方法，我考虑从正中间剪出一个正三角形。根据正三棱柱的特点，侧棱与底面垂直，我考虑从底面正三角形的边出发，剪出三个矩形。剩余的，我想办法再拼成一个正三角形。

师想法很好！其实，考虑三个顶点的对称性和数学美，也应该先从正中间剪出一个正三角形。那么，怎么操作呢？

（学生思考。教师组织全班拿出三角形纸片，动手操作。）

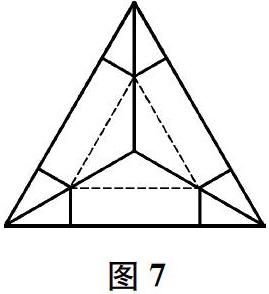
生（出示图7）取正三角形的中心，分别与三个顶点连线;取三条连线的中点再连线，得到一个正三角形，作为一个底面;从三条连线的中点分别向各边作垂线，得到三個全等的矩形，作为三个侧面;剩下三个全等的筝形可以拼成一个正三角形，它与前面的正三角形全等。

师很好！动手操作给了我们启发。请思考一个问题：一定要取正三角形的中心吗？取正三角形内的其他点可以吗？

生不可以。其他点的话，从三条连线的中点分别向各边作垂线得到的三个矩形不全等，宽不一样。

师为什么宽不一样？怎么才能使宽一样。

生三条连线必须是三个内角的平分线。

师很好！利用角平分线的性质，才能剪出三个一样宽的矩形。因此，实际上取的是正三角形的内心。当然，正三角形的中心是内心、外心、重心、垂心的“四心合一”。但是，取内心才具有一般性（可迁移性），而取中心不具有一般性。还有其他剪拼方法吗？

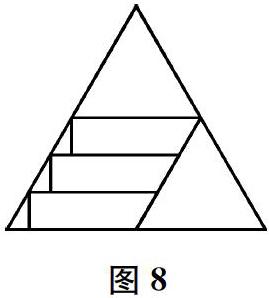
生（出示图8）从两个角剪出两个全等的正三角形，作为正三棱柱的两个底面;将剩下的平行四边形剪成三个全等的小平行四边形，再将每个小平行四边形剪拼成矩形，作为正三棱柱的三个侧面。

师很有创意，有很强的思维灵活性和直观想象力。现在可以讨论第三问了。

生（出示图9）类似正三棱柱的剪拼方法，可取三角形的内心，分别与三个顶点连线;取三条连线的中点再连线，得到一个三角形，作为一个底面;从三条连线的中点分别向各边作垂线，得到三个等宽的矩形，作为三个侧面;剩下三个筝形可以拼成一个三角形，它与前面的三角形全等。

师很好！这里完全可以类比迁移之前正三角形中的剪拼方法。可见，同学们在学习过程中，既要动脑思考，又要动手操作。

参考文献：

[1] 教育部考试中心.中国高考评价体系[M].北京：人民教育出版社，2019.

[2] 徐利治，王前.数学与思维（珍藏版）[M].大连：大连理工大学出版社，2016.

[3] 涂荣豹.数学教学设计原理的构建——教学生学会思考[M].北京：科学出版社，2018.