WSN低功耗低时延路径式协同计算方法
2021-04-22马步云马新策任智源
马步云,马新策,黄 松,任智源
(西安电子科技大学 综合业务网理论及关键技术国家重点实验室,陕西 西安 710071)
0 引言
无线传感器网络 (Wireless Sensor Network,WSN)[1]自提出以来得到快速发展,已被应用到包括医疗[2]、自然环境监测[3]等在内的多个领域。目前的WSN系统利用云平台处理数据[4],然而WSN采集的数据传到云计算中心进行计算产生的通信开销大、时延高,无法有效支撑时延敏感型业务。
针对云计算存在的高传输时延问题,出现了许多利用分布在网络边缘[5]的设备集群进行协同计算的方案。其中,基于步骤可分割的路径式协同计算(路径计算)方案[6-12]采用有向无环图 (Directed Acyclic Graph,DAG) 表征业务,将DAG形式的业务映射到网络边缘设备上以降低任务处理时延,更适合处理复杂的新型信息业务。
但时延降低将导致能耗增加,WSN工作寿命减短,并且WSN通常位于野外,一旦能量耗尽,难以得到及时补充。因此,路径计算如何进行任务映射,使得在能耗约束下业务处理时延最短,成为重要问题。为此,本文将能耗约束考虑进路径计算中,提出了WSN低功耗低时延路径式协同计算方法。
1 云雾网络架构
为了能够利用WSN支撑路径计算的实现,本节基于一种WSN云雾网络架构开展研究,如图1所示。
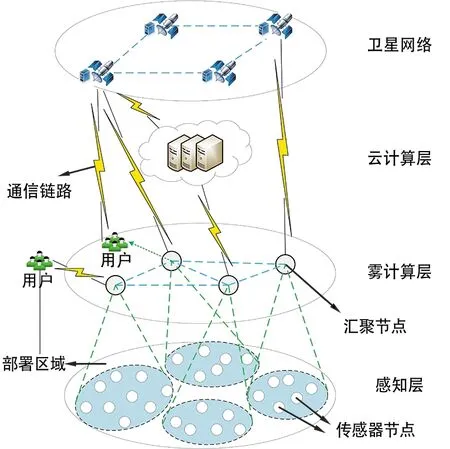
图1 云雾网络架构Fig.1 Cloud fog network architecture
该架构自下而上为感知层、雾计算层和云计算层。感知层由集成一个或多个类型的无线传感器组成,负责对所在区域进行监测。雾计算层由具备较强数据处理能力和通信能力的汇聚节点组成,一方面负责转发和处理感知层产生的数据;另一方面负责将控制中心的命令传达到传感器节点,用户可直接访问汇聚节点获取实时信息。云计算层由具备高性能的服务器集群构成,通过通信链路与汇聚节点相连,对WSN进行监控和管理。同时,当地面通信链路损坏或WSN部署区域缺少通信基础设施时,可利用卫星网络构成通信链路,实现云计算层和雾计算层的通信。
基于此架构,WSN产生的数据无需传输至云端进行处理,而是在云端提前制订好将DAG形式的任务映射到网络设备的任务调度方案,即任务映射策略,并将此策略下发到雾计算层,利用雾计算节点的计算能力逐步完成任务计算,显著降低了任务处理时延。
2 能耗约束下的任务映射策略
基于云雾架构,路径计算技术首先需要将DAG形式的业务图映射至无向图 (Undirected Graph,UG) 形式的雾网络中,如图2所示。
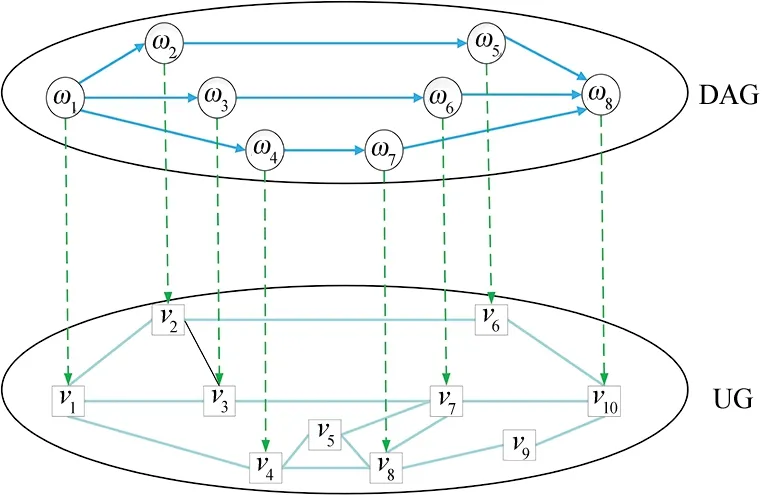
图2 DAG至UG映射示例Fig.2 Example of DAG to UG mapping
2.1 DAG至UG映射规则模型
本节用有向无环图G=(Ω,Γ)表示任务模型。定义Ω={ω1,ω2,…,ωs,ωs+1,…,ωl-1,ωl|s≥1,l>s+1}为G的节点集合,其中,ω1,ω2,…,ωs为s个任务起点,ωs+1,…,ωl-1为中间任务节点,ωl为任务终点。为简化模型,本文仅考虑单任务情况。Γ为G的有向边集合,定义Φ↑(ωi)={ωj|(ωj,ωi)∈Γ}为ωi的前向节点集合。

结合文献[13],图G~图U的映射规则如下:
定义1Ω~V的映射规则为ε:Ω→V,且ε需满足:
(1)
ε将Ω的任务起点ω1,ω2,…,ωs映射为V的任务发起节点v1,v2,…,vs;将中间任务节点ωs+1,…,ωl-1映射为任意中继节点vs+1,…,vt-1;将任务终点ωl映射为与用户直连的节点vt。
定义2Γ~P的映射为Υ:Γ→P,且Υ需满足:
Υ(ωi,ωj)=Pathε(ωi),ε(ωj)。
(2)
Υ将集合Γ中的有向边映射为图U中的节点ε(ωi)~ε(ωj)的最短路径Pathε(ωi),ε(ωj)。
2.2 时延模型
上述映射规则可能会产生不同映射方案,导致不同的时延。为进一步降低时延,本小节基于2.1小节提出时延模型。
子任务ωi在某次映射关系中的时延可以表示为:
(3)

则图G的任务处理时延为任务终点ωl的时延为:
T(G)=T(ωl)。
(4)
2.3 能耗模型
通过时延模型可计算出不同映射的任务处理时延,进而求出最短时延,但WSN能量有限,需要在能耗约束下完成任务计算,因此基于2.1和2.2小节提出能耗模型。
根据文献[14],WSN的能耗主要分为空闲能耗和活动能耗,忽略状态转换时的能耗,则网络节点vi的能耗为:
(5)
2.3.1 空闲能耗
空闲能耗指节点处于空闲状态时的能耗,根据文献[15]所述,空闲能耗约占节点整体能耗的一半,因此必须考虑空闲能耗。
① 映射节点ε(ωi)的空闲能耗为:
(6)

(7)
2.3.2 活动能耗
① 映射节点ε(ωi)的活动能耗包括计算能耗和传输能耗,如式(8)所示:
(8)

(9)
由式(6)和式(8)可得,映射节点ε(ωi)的总能耗如式(10):
(10)
(11)
整个雾网络的总能耗为:
(12)
令整个雾网络所含有的最大能量为Emax,则在某次任务G内,网络所产生的能耗需小于等于最大能耗:
(13)
2.4 DAG至UG映射规则优化模型
仅根据2.1~2.3小节很难构建优化问题,为方便后续优化问题建立,基于上述小节给出DAG至UG映射规则的优化模型,并建立二值优化问题。
定义3子任务节点ωp和雾网络节点vq的映射关系如下:当xωpvq=1时,ωp映射为vq;当xωpvq=0时,ωp不会映射为vq,则xωpvq满足:
xωpvq∈{0,1}∀ωp∈Ω,∀vq∈V。
(14)
基于定义3,ωp~vq的映射可以构建为l×t的映射矩阵X,如式(15):
(15)
则式(6)所表示的子任务ωi的时延可表示为式(16):
(16)
任务G的时延可表示为X的函数,如式(17):
T(G)=F(X)。
(17)
式(10)所示的映射节点ε(ωi)的总能耗可表示为:
(18)
(19)
则能耗约束下,图G~图U的最优映射关系建模如下:
X=argmin(F(X))

(20)
则求解图G~图U的最优映射关系可建模为求解式(20)的二值优化问题。
3 BPSO算法
(21)
(22)
第i个粒子在第n次迭代中,速度更新公式[19]为:
(23)

BPSO算法的位置更新公式如式(24)和式(25):
(24)
(25)
本算法的适应度函数如式(26):
f(X)=T(G)=F(X) 。
(26)
综上所述,在求解上述时延优化模型时,BPSO算法的具体步骤如算法1所示。

算法1 BPSO算法1. fori=1:M do2. 初始化粒子的速度与位置3. 通过式(29)计算粒子适应度值4. 设置当前位置为粒子最佳位置pbest5. 通过比较得出全局最优位置gbest6. end for7. fork=1:Nmax do8. fori=1:M do9. 通过式(23)~式(25)更新粒子的速度和位置10.通过式(26)计算粒子适应度值11.If f(Xi+1) < f(pbest) then12. pbest = Xi+1;13. f(pbest) = f(Xi+1);14.end if15.If f(pbest) < f(gbest) then16. gbest = pbest;17. f(gbest) = f(pbest);18.end if19. end for20. end for21. Output:f(gbest)
4 仿真实验及分析


图3 仿真所用任务图Fig.3 Task graph for simulation
考虑到WSN一般通过飞机等形式随机投放到监测区域内,本次仿真利用Matlab随机生成网络拓朴图,如图4所示。
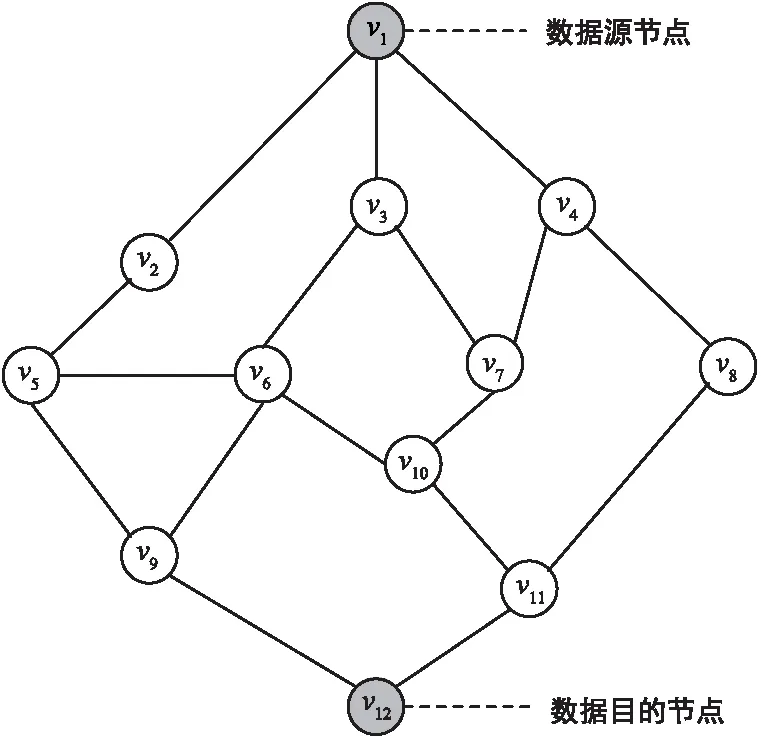
图4 仿真所用网络拓朴图Fig.4 Network topology used in simulation
仿真平台为Matlab,所用参数均参照文献[16-17,20-24]设置,如表1所示。其中,fc为云服务器计算能力,Rc为云雾链路的数据传输速率,ffog为雾计算节点的计算能力,Rfog为雾链路数据传输速率,emax为单个节点的最大能量。
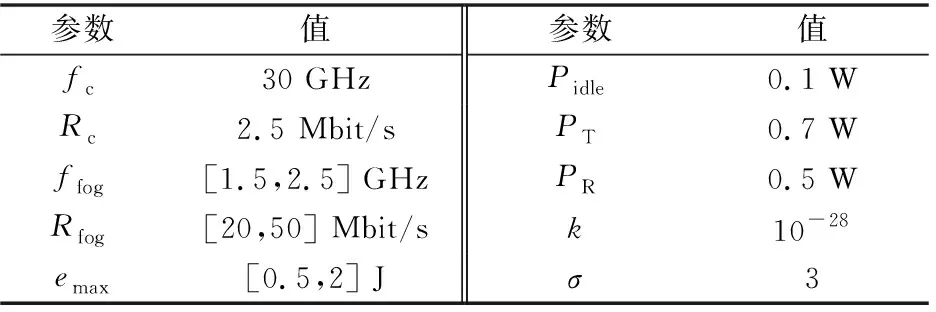
表1 系统参数
由表1可知,单个节点的最大能量为[0.5,2] J,结合图4可知,雾网络的最大能量Emax为[6,24] J。BPSO算法的基本参数为:种群规模M=500,最大迭代次数Nmax=1000,加速因子γ1=γ2=1,惯性权重ρ=1。
4.1 云计算与路径计算时延性能对比
为验证本文所提出的路径计算方法的有效性,对比了3种不同业务的云计算和路径计算的时延性能,并用Emax=6 J与Emax=24 J两条线表示路径计算的时延性能范围。仿真结果如图5所示。

(a) gzip ASCII压缩任务
由图5可知,路径计算在处理不同类型任务时,开始均表现出Emax=6 J与Emax=24 J的时延无明显差别,而当任务量大于某阈值时,Emax=6 J的时延高于Emax=24 J的现象。原因是:当任务量较小时,最佳映射产生的能耗低于Emax=6 J,因此二者无明显差别;随着任务量的增加,能耗也逐渐升高,当达到某阈值时,最佳映射产生的能耗高于Emax=6 J。为满足能耗约束,不得不牺牲时延,将子任务映射至计算能力较差的节点上。
同时,随着任务复杂度不断增加,路径计算的任务处理时延急剧增加,而云计算增长缓慢。原因是任务复杂度仅影响计算时延,而云计算的计算能力较强,因此任务复杂度的变化对云计算影响甚微;而汇聚节点计算能力较弱,因此当任务复杂度增加时,路径计算的时延急剧增加,并且有逼近云计算的趋势。据此可推测,当处理更复杂的任务时,云计算的时延性能将优于路径计算。因此,路径计算适合处理复杂度较低的任务,而云计算适合处理复杂度较高的任务。
4.2 BPSO算法与其他算法时延性能比较
为验证BPSO算法在解决路径计算方案的有效性,比较了处理多种任务时BPSO算法与加权轮转法(WRR)、随机动态算法(Pick-KX)以及贪婪负载均衡算法(Greedy-LB)的任务处理时延,如图6和图7所示。
图6仿真了不同能耗约束下多种算法的时延性能,此时任务量取10 Mbit。由图6可知,随着Emax的增加,4种算法的任务处理时延均表现出先下降、后收敛于某一数值的趋势,且BPSO算法的任务处理时延明显低于其他3种算法,以x264 CBR编码任务为例:当Emax=24 J时,BPSO、Greedy-LB、WRR以及Pick-KX的时延分别为4.609,6.733,7.754,7.936 s,BPSO算法相比于其他3种算法分别降低了31.55%,40.56%,41.92%。
图7仿真了不同任务量约束下多种算法的时延性能,此时,能耗约束取24 J。由图7可知,当数据量D<2 Mbit时,4种算法时延差别不明显;但当任务量D>4 Mbit时,随着任务量的增加, BPSO算法的时延明显低于其他3种算法。以x264 CBR编码任务为例:当任务量为10 Mbit时,BPSO、Greedy-LB、WRR以及Pick-KX的时延分别为3.91,6.608,6.87,7.122 s,BPSO算法相比于其他3种算法分别降低了40.83%,43.09%,45.10%。
这是因为Pick-KX算法随机选取雾网络节点进行映射,并未考虑节点的计算能力;WRR算法根据节点的计算能力大小关系进行映射,Greedy-LB算法通过选取当前负载最小的节点进行映射,但WRR和Greedy-LB均未考虑网络边的传输能力,仍不是最优;BPSO算法综合考虑节点计算能力和网络边的传输能力,可达到有效降低任务处理时延的目标。
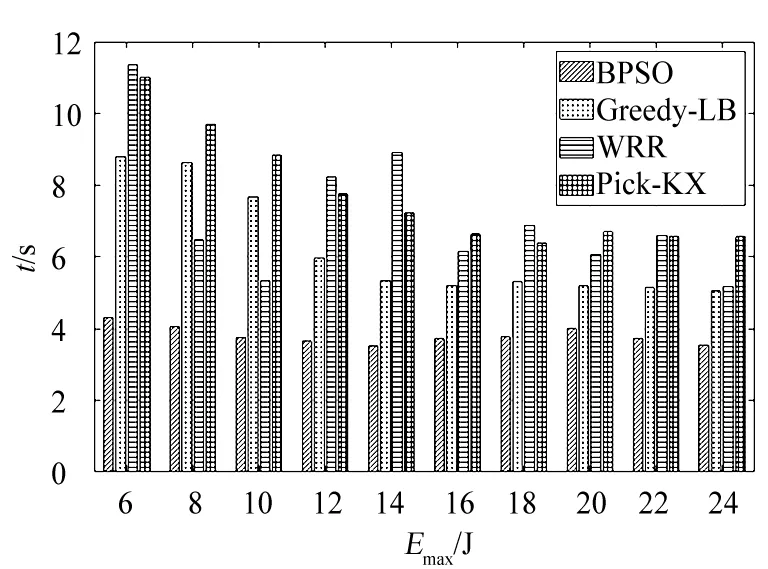
(a) gzip ASCII压缩任务

(a) gzip ASCII压缩任务
5 结论
针对WSN云计算模式处理任务时效性较差的问题,研究了一种云雾网络架构,并将路径计算技术引入WSN中,解决了将采集到的数据传回云中心进行处理而引起的高传输时延问题。针对汇聚节点能耗增加导致寿命缩短的问题,提出了能耗约束下的路径计算方法。仿真结果表明,在相同的能耗约束下,相比其他算法,基于BPSO算法得出的映射方案能有效降低业务处理时延。但本文所提出的映射方案仅限于静态网络,并未考虑DAG映射到动态网络的情况,如何将DAG映射到动态网络将是下一步的研究方向。
