基于非线性超声谐波法的混凝土构件应力检测
2021-04-21刘鹏飞王英瞩李祚华刘海涛
刘鹏飞,王英瞩,李祚华,刘海涛,滕 军,陈 杰
(1.深圳市建筑设计研究总院有限公司,深圳 518031;2.哈尔滨工业大学(深圳) 土木与环境工程学院,深圳 518055)
目前,混凝土工作应力的传统测试方法主要采用局部破损法[1],如:应力释放法、钻芯法、拔出法和射击法等。这些应力检测方法都是基于材料应力-应变关系,通过测量混凝土的应变来间接反映混凝土的应力水平。然而,混凝土弹性模量的实测值与规范取值之间是存在差别的,且混凝土性质复杂,局部所测量的应力并不能反映混凝土的平均应力水平,导致混凝土的测试应力与实际应力不相符;同时,这些方法破坏了混凝土的局部结构,其测量结果也常受外界环境包括切割扰动和温度、湿度变化等因素的影响。
近年来的研究结果表明,弹性介质中的微裂纹会打破入射的超声波和接收到的弹性波响应之间的比例关系。其中,各频率的再分布是微观结构演化的主要现象之一[2]。当单周期正弦波穿越弹性介质时,其与介质内部的非线性散射体相互作用会产生新的谐波分量。混凝土的早期退化特性,如微裂隙、微缺陷等微观结构变化与非线性声学效应密切相关。
因此,笔者根据非线性参数调制理论建立有限元仿真模型,分析该方法对应力检测的敏感性。搭建了单轴加载非线性超声波应力检测系统,以不同强度等级的混凝土试样为检测对象,研究在不同应力水平下,混凝土中传播的超声激励信号与混凝土裂纹发展状态的相互作用,以非线性系数为检测的声学参数,分析非线性系数与应力的关系。文章实现了非线性超声谐波检测技术对混凝土应力状态的有效检测,为非线性参数谐波技术应力检测的定量表征提供了参考。
1 非线性超声谐波应力检测方法
非线性超声谐波调制的基本原理如图1所示,在检测过程中,向被测材料输入频率为ω0的超声波。如果材料中没有裂纹,则激励超声波信号的波形不变;如果存在裂纹,且随着荷载的增加裂纹扩展,则材料内部空间介质的不连续在超声波作用下会产生非线性效应,缺陷处的质点振动速度发生改变,从而引起波形畸变,产生以主频率为倍数的非线性超声谐波信号[3]。

图1 非线性超声谐波调制的基本原理示意
介质中声波传播的波动方程是由介质的运动方程、连续性方程和物态方程推导出的[4-5]。以一维纵波为例,固体介质的非线性应力应变关系为
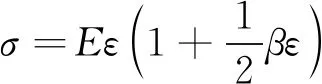
(1)
式中:β为二阶非线性系数;s为混凝土受到的应力;E为弹性常数;e为混凝土的应变。
固体介质中质点在x方向上的运动方程为
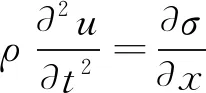
(2)
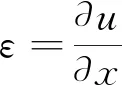
(3)
式中:μ为质点位移;t为质点运动时间;ρ为混凝土变形前的密度。
混凝土是一种介于离散介质和连续介质之间的材料。从离散模型出发,假设一列沿x轴方向传播的压缩纵波进入混凝土介质中,结合式(1),可以得到离散模型非线性超声纵波波动方程

(4)
E与纵波声速c的关系有
c2=E/ρ
(5)
因此式(3)也可表示为
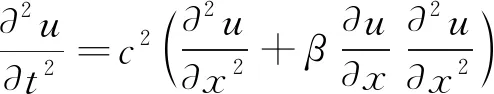
(6)
设式(4)的初始条件为
u(0,t)=A0sinωt
(7)
式中:A0为初始振幅;ω为角频率。
用逐级近似微扰法可求得式(6)的解为
u(x,t)=A0sin(ωt-kx)+
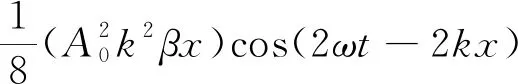
(8)
式中:k为波数。
波在非线性介质材料传播时频率发生了改变,除原频率ω外,还出现了频率为2ω的高阶谐波。
A1=A0
(9)
式中:A1为基波幅值。
二次谐波幅值A2为

(10)
进而可以得到材料的非线性系数为

(11)
在混凝土应力检测试验中,超声频率、波速、声程均保持不变,则

(12)
根据式(12),对于给定的声波频率和波传播距离,通过对基波幅值A1和二次谐波幅值A2的测量,就可以确定材料的超声非线性系数。在加载过程的非线性系数和应力关系中,参考混凝土材料的应力应变本构关系,由于单轴受压加载试验下混凝土材料应力应变的关系曲线接近于二次抛物线[6],将非线性系数和应力关系用多项式表达为
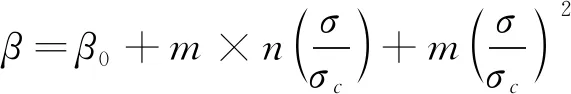
(13)
式中:σc为混凝土材料抗压极限应力;β0,n和m均为与材料有关的非线性参数。
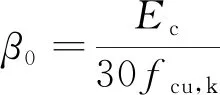
(14)
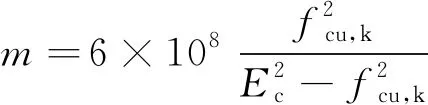
(15)
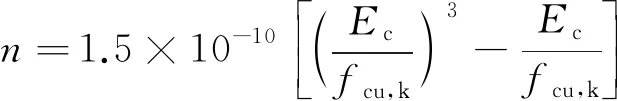
(16)
式中:Ec为混凝土弹性模量;fcu,k为混凝土立方体的抗压强度。
不同强度等级下混凝土的非线性参数如表1所示。
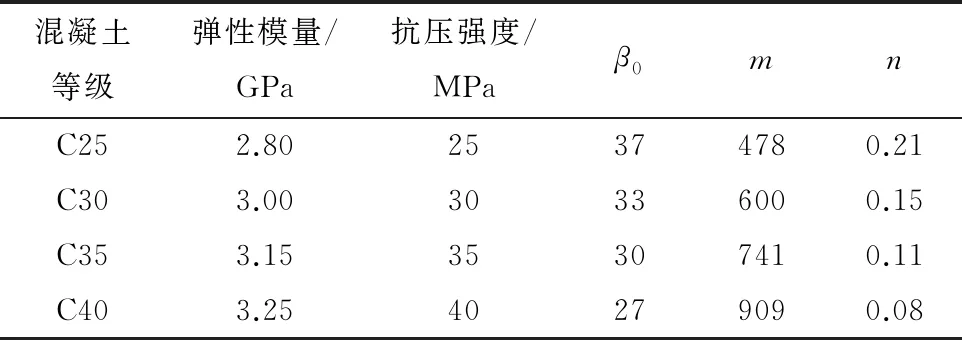
表1 不同强度等级下混凝土的非线性参数
2 有限元仿真分析
2.1混凝土构件声学检测基本模型设计
模拟建立C30混凝土板仿真模型(见图2),尺寸为0.1 m× 0.1 m×0.003 m(长×宽×高)。密度为2 400 kg·m-3,弹性模量为30 GPa,泊松比为0.2。混凝土自振频率为50 kHz100 kHz,模拟时采用频率为50 kHz的超声波激励。
以C30等级的混凝土为例,确定超声波在混凝土材料中传播的波速c和波长λ分别为

(17)
λ=c/f
(18)
式中:f为超声波的频率。
在创建单元网格上,应力波随时间沿着与荷载方向垂直的方向传播,且需要足够精细的网格捕捉应力波,对裂纹局部进行更细致的划分,则每个波长需要20个单元跨度。
Δx=λ/20
(19)
式中:Δx为网络尺寸。
微裂纹区域网格划分如图3所示,微裂纹区域采用精细网格进行结构化网格划分,远离微裂纹区域的网格适当放大,中间采用扫掠网格过渡。

图3 微裂纹区域网格划分示意
在C30等级的混凝土模型中,对于不同弹性模量的混凝土,为了统一变量参数,模型最大网格尺寸为0.003 m,最小网格尺寸记为Δxmin,为0.000 2 m。
时间增量步Δt选取要保证每个增量步时长比超声波在一个单元传播的时间短,以及时捕捉超声波,其应满足
Δt≤Δxmin/c
(20)
根据超声波传播原理,在混凝土板模型左端边界取信号输入点,并施加正弦应力波,信号参数同试验所用信号参数,频率为50 kHz,采样频率为25 MHz,采用位移加载使材料内部质点产生振动,模拟超声波的激励效果,在混凝土板模型右端边界取信号输出点。
由于模型裂纹设置主要采用竖向发展形态,所以将裂纹定义为自接触,接触作用属性为法向硬接触。切向行为摩擦公式定义为罚接触,摩擦系数设为0.5。
2.2 非线性系数与应力相关性分析
弹性模量的敏感性分析选取C30混凝土模型的闭口模型,分别模拟加载后刚度退化的弹性模量,得到0 MPa,1 MPa,3 MPa,6 MPa,9 MPa,12 MPa,15 MPa,18 MPa,21 MPa应力下的混凝土构件的非线性响应。对于不同应力状态,分别取对应的材料弹性模量和裂纹发展状态进行模拟,各应力状态下混凝土模型声信号频谱如图4所示。
由以上模拟分析可知,在未加载应力的情况下,混凝土模型为零裂纹状态,非线性响应不明显。随着荷载的施加,非线性响应越来越明显,非线性系数随应力的增加而增加,非线性系数与应力比的定量关系如图5所示。
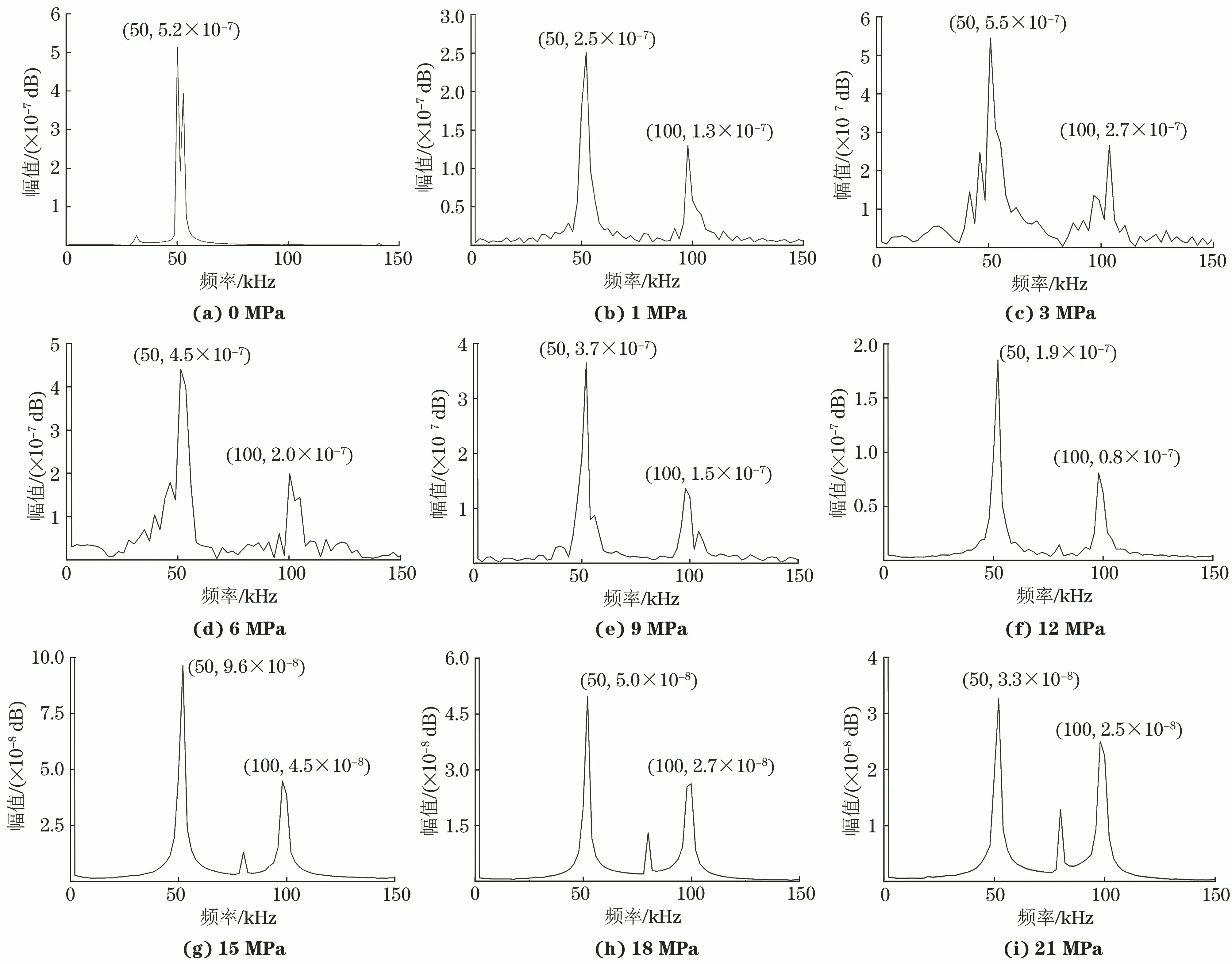
图4 各应力状态下混凝土模型超声信号频谱
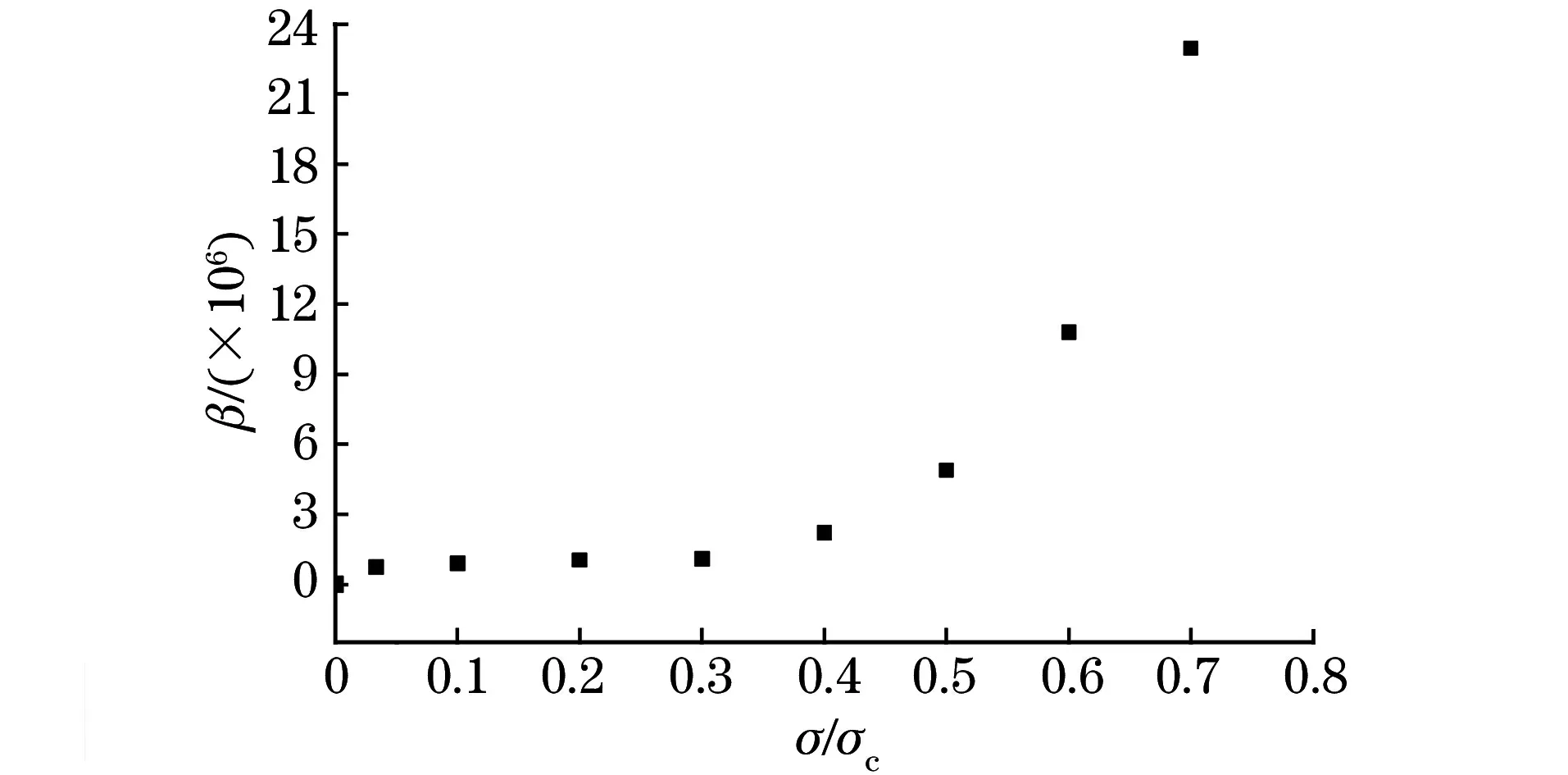
图5 非线性系数与应力比的定量关系
3 试验方法
3.1 混凝土构件声学检测试验设计
试验选取强度等级分别为C25,C30,C35和C40的混凝土试样进行加压试验,试样规格为100 mm×100 mm×100 mm(长×宽×高)的正方体。选取的粗骨料粒径为520 mm的石灰岩碎石,细骨料粒径为510 mm的石灰岩碎石,水泥为普通硅酸盐水泥。
制备前按照《普通混凝土配合比设计规程》确定各成分的比例及用量。混凝土拌和物的湿表观密度为2 400 kg·m-3,将试样按不同等级的混凝土材料配合比标准进行分组编号,并立即在水中湿养28 d,使其保持完全饱和水状态。
采用一发一收法进行测试,分别选用频率为50 kHz的发射探头和100 kHz的接收探头,探头外观如图6所示。选用医用凡士林为耦合剂。

图6 超声波探头组合外观
3.2 单轴受压加载试验设计
混凝土在实际工程中的受力一般要低于其强度极限值的50%[7],以C30等级的混凝土为例,根据最新修订的 《混凝土强度检测评定标准》 规定加载等级应按破坏荷载的1/151/10进行分级加载,该等级混凝土的破坏荷载约为300 kN。测试时,以每级荷载为20 kN,加载速率为3 kN·min-1的分级加载方式进行均匀加载,直到混凝土试样被压坏。
在加载之前,先采集试样在零荷载状态下的超声波信号,待每一级荷载加载完毕且试样不再变形后,再采集该级荷载下的超声波信号。
3.3 超声波应力检测试验
将浸泡后的完全饱和状态的混凝土试样都取出,分别进行荷载试验,试验过程中通过控制加载等级来实现对加载过程中混凝土的超声波检测,进而比较不同配合比混凝土的超声波非线性参数的变化。检测系统结构示意如图7所示。

图7 非线性超声谐波法应力检测系统结构示意
3.4 非线性参数的提取
(1) 在数学软件中采用快速傅里叶变换(FFT)实现对声波信号的处理,将时域信号转化为频域信号。
(2) 在声波时域和频域分析的基础上,通过对采集的超声波信号进行分析处理,提取出非线性超声参数,以此研究单轴荷载作用下混凝土的超声波参数随应力的变化规律。
(3) 由公式获得材料的非线性系数,绘制β-σ图,并与理论曲线进行对比。
3.5 应力-非线性系数定量表征方法研究
通过试验,对比C25,C30,C35和C40等级的混凝土试样非线性系数随荷载的变化趋势,试验结果如图8所示。其中,将表1中的相应参数代入式(13),得到各个强度等级的混凝土材料的理论曲线。
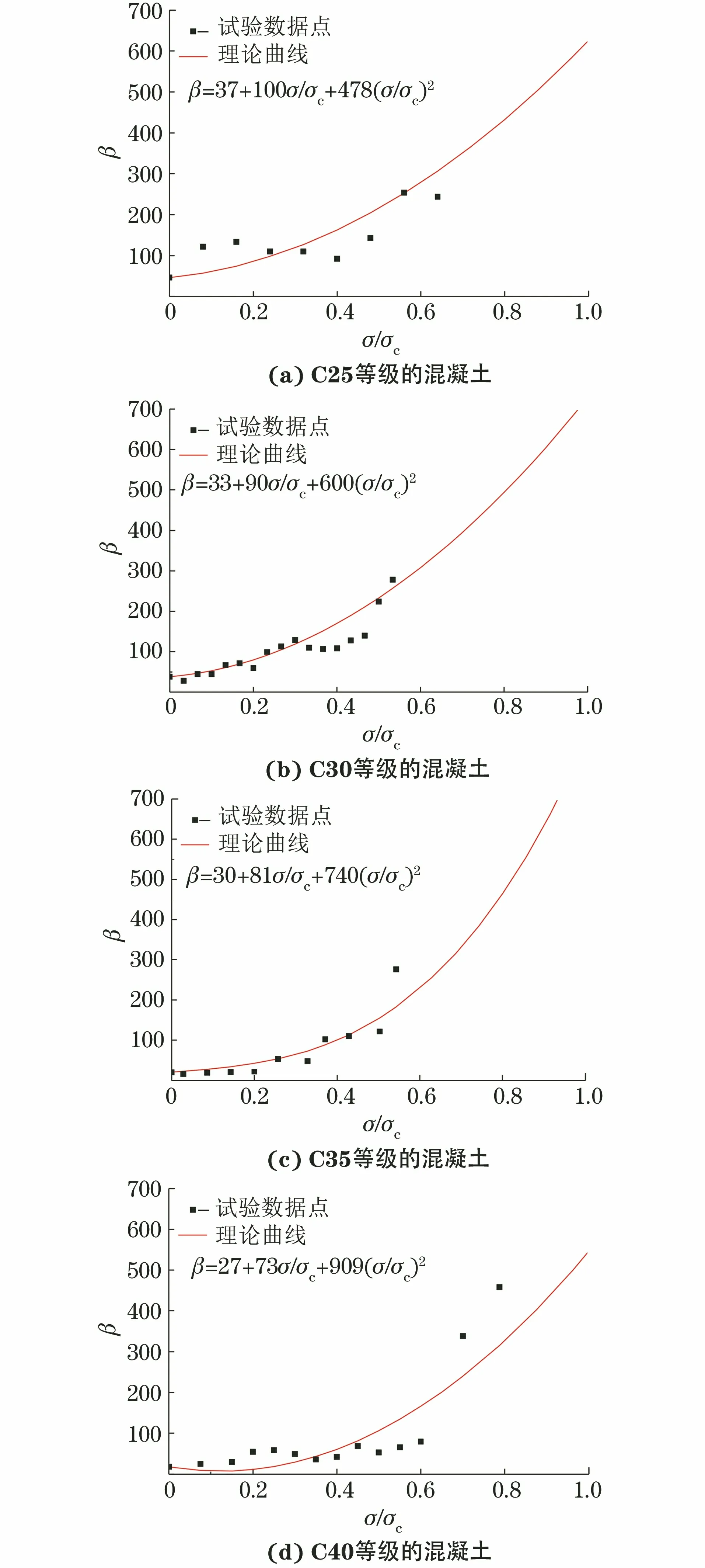
图8 不同等级的混凝土非线性系数与应力比的关系
对比图8中的试验数据点和理论曲线,在极限应力的前50%~60%的早期应力阶段,除C25等级的混凝土吻合效果稍差外,其余混凝土试验数据点均落于理论曲线附近,吻合率较好。这是由于低强度混凝土内部骨料结构受应力影响较大,超声波在材料内部的传播也受到较大影响。后期随着应力的增加,混凝土试样逐渐被压出裂缝,此时探头出现了不同程度的滑脱,导致试验点远离理论曲线。由于混凝土在实际工程中的工作应力一般不高于其强度极限值的50%,所以在该应力范围内的检测结果满足工程上的需求。
对比不同强度等级混凝土的非线性系数和应力关系可以发现,系数m随混凝土强度等级的增大而增大,系数n随混凝土强度等级的增大而减小。由式(13)可知,m控制曲线的整体陡缓程度,m越大曲线越陡,高应力阶段的数据点起决定性作用。n控制曲线早期应力阶段的陡缓程度,n越大曲线早期越陡,早期应力阶段的数据点起决定性作用。
4 结语
(1) 基于非线性谐波效应,将混凝土的声学特性和力学特性建立联系,结合经典声波动理论获得了表征应力的表达式。
(2) 建立了混凝土轴向应力与非线性声学响应参数的本构关系模型,得到的本构关系为二次多项式,其中包含了与混凝土材料有关的应力-非线性常数。
(3) 搭建了超声波检测加载混凝土试样试验系统,在不同压力水平下进行了超声检测试验和仿真模拟,其结果验证了提出的本构模型的有效性。
