基于超声Lamb波的双曲线定位损伤成像方法

2021-04-21韩伟，冯侃，骆英

无损检测 2021年4期

韩伟，冯侃，骆英

(江苏大学土木工程与力学学院，镇江 212013)

由于复合材料制作工艺复杂、服役环境恶劣，所以其不可避免地会产生各种各样的损伤。损伤的产生会降低结构强度，危害结构安全。尽管大多数复合材料结构都按照损伤容限准则设计[1]，但在损伤出现并扩展之前，对其进行检测与评估尤为重要。

Lamb波具有传播距离远、能量衰减小以及检测范围大等优势，在板状结构的无损检测中应用广泛[2-6]。其中,基于Lamb波的椭圆定位方法[7-8]因具有简单高效、方便快捷等优势，在板状结构的损伤定位应用中得到了大量的研究与发展。椭圆定位方法需要事先知道导波在材料中的传播速度，复合材料中的导波传播速度往往难以获取并且具有各向异性特征，因此难以获取导波传播时间。同时由于复合材料的频散效应使波形畸变与拉长，也降低了获取导波传播时间的准确性。针对椭圆定位方法对复合材料损伤检测的局限性方面，笔者提出了一种全新的双曲线定位方法(Hyperbolic Location Method,HLM)，以COMSOL软件进行数值模拟分析，利用双曲线定位法成功实现了正交各向异性复合材料板的损伤定位。

1 双曲线定位方法

1.1 基本理论

由于导波的频散、多模态等特性,以及复合材料的各向异性特征，Lamb波在复合材料中的传播十分复杂，所以完全依赖导波传播速度的椭圆定位方法无法应用于复合材料中或者其损伤定位精度受限。基于此，提出了双曲线定位法，双曲线定位法依据双曲线上任一点到两个焦点的距离差为定值的思想，以相位差确定双曲线实轴，相较于椭圆定位法，该方法可以在无需材料参数信息和频散关系，并且在不受复合材料各向异性特征影响的情况下实现了复合材料的损伤检测。

图1为双曲线定位方法理论示意，在基于超声导波的损伤定位过程中，导波在结构中传播并与损伤相互作用，其中损伤可以看作是二次波源，此时通过分析损伤散射波信息即可实现损伤定位。在双曲线定位法理论中，通过等间距的若干线性传感器阵元接收损伤散射信号，在如图1所示的每一对接收阵元中，由于阵元间距足够小，则在误差容许范围内，将损伤散射波沿损伤源传播到每一个接收阵元的波速看作是相同的，因此复合材料的各向异性不会影响双曲线定位方法。通过傅里叶变换可以得到一对接收阵元处损伤散射信号的相位谱为

(1)

式中：u(xm,t)为一对接收阵元接收到的损伤散射信号;xm为接收阵元位置;Im和Re分别为傅里叶变换后复数值的虚部与实部;F为接收阵元处损伤的散射信号;φ为损伤散射信号各频率分量对应的相位。

经过傅里叶变换后，每个损伤散射波对应的谐波分量为

(2)

两阵元分别接收的损伤散射信号的每个频率所对应的相位差与传播路径之差Δl的关系为

(3)

图1 双曲线定位方法理论示意

沿着接收阵元到损伤散射源的反向路径上反转每个频率对应的相位，可以得到损伤散射源处损伤散射信号的初始相位Φω为

Φω=ω-Δφω/Δl

(4)

此处需要强调，应用双曲线定位方法的前提是接收阵元间的间距必须小于导波在结构中传播的半波长，此时可以认为，误差在容许范围内，每条传播路径下的导波传播速度相同，否则各向异性所导致的导波传播速度差将会影响损伤成像精度。

在损伤散射源处，每一对接收阵元所重构的损伤散射信号的初始相位在理论上应具有较高的一致性，因此损伤成像指标DI定义为重构相位的相似性，如式(5)所示。

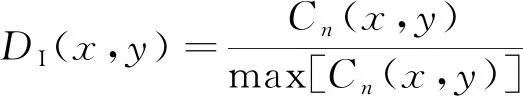
(5)

式中：Cn(x,y)为重构相位在位置(x,y)处的相关系数，以相邻3个接收阵元为一组;n为每一组接收阵元的序号。

相位相关系数定义为

(6)

由式(4)可以得出,双曲线定位法的成像曲线为一条经过损伤的双曲线，在一组3个等间距的接收阵元中，每一对接收阵元按照式(4),通过相位差的变化求得的初始相位理论上是相同的，即相位差就是双曲线上每一点到焦点的距离之差，双曲线实轴即为通过相位差变化所得到的损伤散射信号在损伤处的初始相位Φω。双曲线定位法不涉及频散关系,并且无需材料参数，同时相位求解过程沿导波传播路径进行，材料的各向异性不影响其有效性。

1.2 数据融合

图像数据融合[8]是指将多幅图像通过数学方法合成，从而获得改进的图像。在双曲线定位理论中，由式(4)可知，其成像几何特性为一条经过损伤的双曲线，其中双曲线的半实轴值为Φω/2。通过对多组测点所得的成像双曲线进行加法融合，其曲线交点即为损伤位置。

图2 双曲线定位损伤成像方法原理示意

根据双曲线定位法理论，将复合材料板状结构分割成如图2所示的离散单元。将所有单元的边界点看成损伤可能存在的位置，通过双曲线定位法重构每一单元边界点的相位，并计算相位的相关系数。单元边界点的相位相关系数即是损伤成像矩阵的像素点，若该单元边界点为损伤，则相位相似性高，在损伤成像结果中将以较高的像素值重点显示。

通过式(7)可分别求得x轴与y轴两条线性阵元的n组以相关系数为成像指标的成像矩阵

(7)

以同一方向线性接收阵元中的3个相邻阵元为一组，n为该方向下的阵元组序号。

将x轴方向n组成像矩阵与y轴方向n组成像矩阵按照式(8)进行加法融合，即可得到最终成像结果。

(8)

2 数值模拟

以正交各向异性复合材料板为研究对象，其结构及阵元设置如图3所示，板的尺寸(长×宽×高)为200 mm×200 mm×1 mm。激励源位于板的中心，信号接收阵元设置为坐标轴正半轴上2条线性阵列。将直径10 mm的通孔当成损伤，其位置坐标为(20 mm,30 mm)。正交各向异性复合材料参数如表1所示(表中，E为各方向的弹性模量;G为各方向的剪切模量;ν为泊松比)。

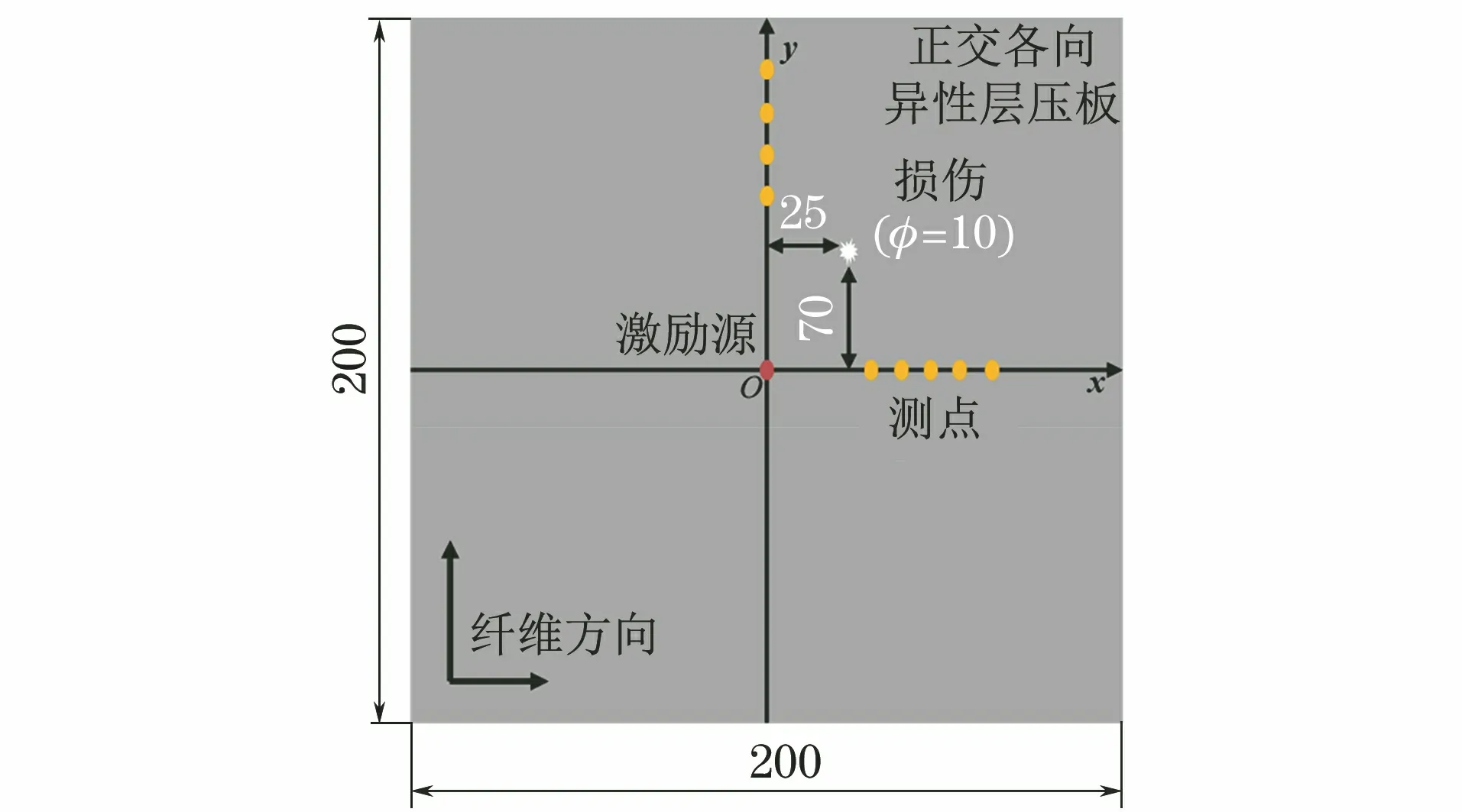
图3 复合材料板结构与其阵元设置示意

表1 正交各向异性复合材料参数

2.1 激励荷载选择与设置

Lamb波在结构中具有多模态特性且受频散效应的影响，其信号复杂并难以分析。窄带激励受频散影响相对较小，波形畸变不显著，信号简单且利于分析。双曲线定位法采用汉宁窗调制的五峰波窄带信号作为激励信号，如式(9)所示。

(9)

式中:A为激励信号幅值;fc为中心频率，选取100 kHz。

激励信号的时域图和频域图如图4所示。

图4 激励信号时域图与频域图

2.2 网格划分和时间步长

模型的网格划分尺寸Δl与导波在结构中传播的波长相关，网格尺寸的设置需要兼顾精度与效率。因此,为了在满足计算精度的条件下同时保证求解效率，网格尺寸应满足式(10)。

Δl≤λmin/10

(10)

式中：λmin为模型中Lamb波的最短波长。

同理，为了兼顾有限元计算结果的准确性与效率，在有限元中求解的时间步长Δt应该满足数值计算的稳定性要求。根据Newmark时间增量方案，复合材料板中的Lamb波在传播一个周期的时间内至少包含20个时间步长。

Δt≤1/(20fmax)

(11)

式中：fmax为频带中的最大频率值。

该研究以中心频率为100 kHz，A0模态为主导的超声Lamb波为激励信号，其对应的波长λ为10.9 mm，综合考虑，有限元仿真中模型的网格尺寸设置为1 mm，时间步长选为0.01 μs，兼顾精度要求与计算效率。

2.3 双曲线定位方法结果

图5为通过有限元计算得到的正交各向异性复合材料板各时刻波场图，复合材料的正交各向异性特征使导波传播速度对方向具有依赖性，因此波阵面呈现近似菱形。

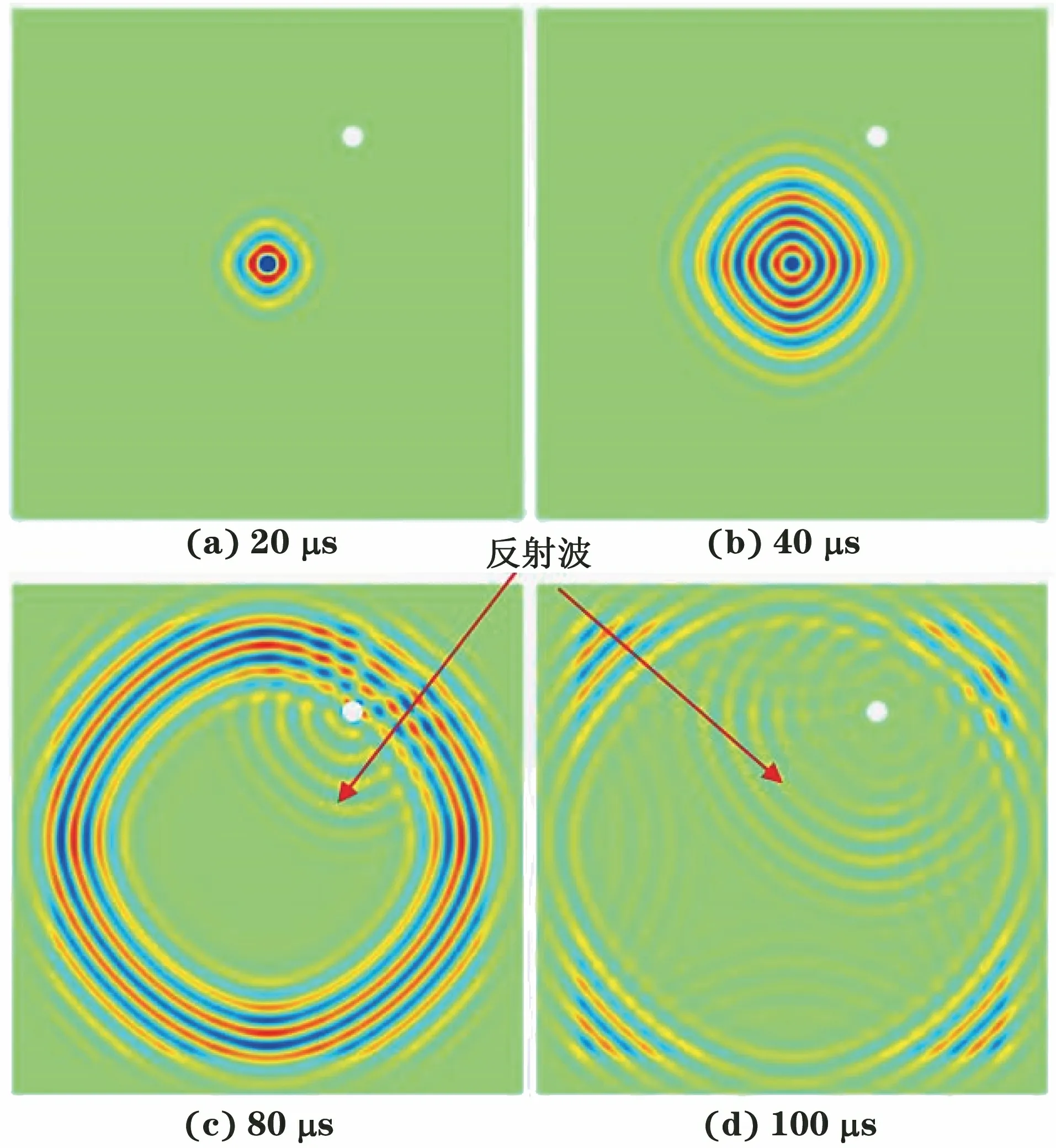
图5 正交各向异性板各时刻波场图

2条位于坐标轴正半轴的线性阵元用于接收损伤散射信号，接收阵元位置与数量如表2所示。根据双曲线定位法理论，阵元间距需满足误差要求，此处间距为1 mm。提取每个测点的离面位移信号用于损伤定位成像，测点的信号如图6所示。

表2 接收阵元位置与数量 mm

图6 测点的直达波与损伤散射波示意

根据双曲线定位法理论，通过3个间距为1 mm的线性阵列即可获得成像矩阵，图7为分别通过x轴与y轴的3个测点所得到的成像矩阵。

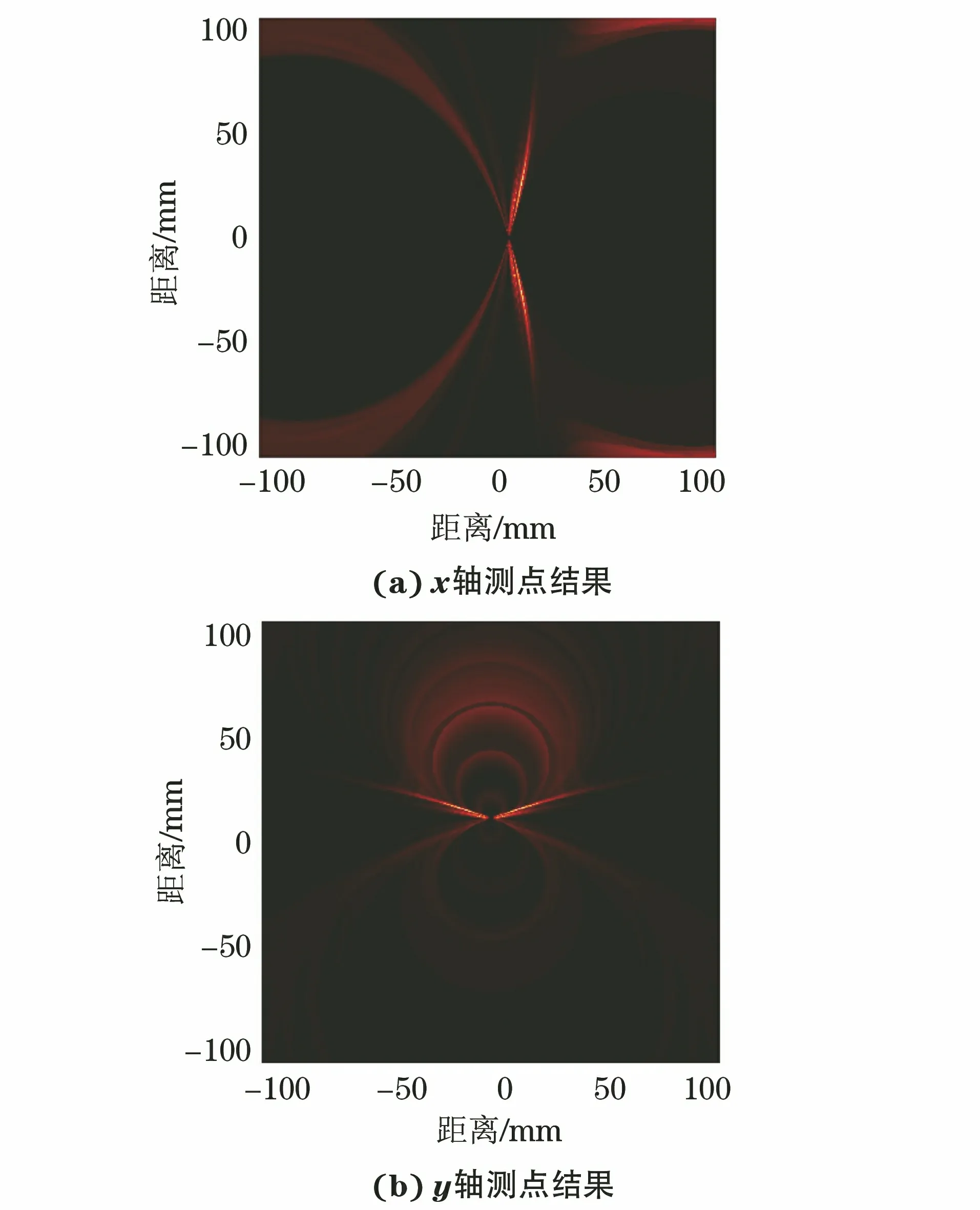
图7 两组线性测点成像结果

从图7可以看出，该双曲线的实轴即为通过相位差变化所得到的损伤散射信号在损伤处的初始相位Φω。根据数据融合方法，将不同组测点所获得的成像曲线进行加法融合，即可实现双曲线在损伤处相交，从而实现损伤定位。将图7所示的成像结果进行加法融合后，得到最终的双曲线定位损伤成像结果如图8所示。该方法在材料参数未知的情况下实现了损伤定位，同时过程中不涉及材料频散关系且不受材料各向异性的影响，因此双曲线定位法可以较好地应用于复合材料的损伤检测中。